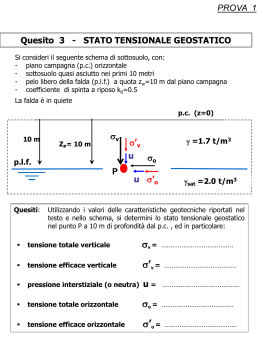
DIDATTICA DI DISEGNO E PROGETTAZIONE DELLE COSTRUZIONI
PROF. CARMELO MAJORANA
ING. LAURA SGARBOSSA
MODULO UNO
IL PROBLEMA DELLA TRAVE DI DE SAINT VENANT (PARTE A)
•
MODULO PER LO SPECIALIZZANDO
•
Modulo 01
IN QUESTO MODULO: IL PROBLEMA DELLA TRAVE DI DE SAINT VENANT;
DISCUSSIONE CRITICA DELLA SOLUZIONE
1.1 Il problema della trave di De Saint Venant: introduzione
1.2 Il metodo semi-inverso
1.3 Il principio di De Saint Venant
1.4 Le caratteristiche della sollecitazione
1.5 Proprietà dello stato di tensione nella trave di De Saint Venant
1.6 Soluzioni del problema di De Saint Venant
1.1 Il problema della trave di De Saint Venant: introduzione
Il problema di De Saint Venant consiste nel determinare la soluzione del problema di
equilibrio elastico per un cilindro, per semplicità retto, detto trave.
Si considerino per lo studio di tale problema le seguenti ipotesi:
•
per la trave:
- corpo continuo dotato di tre dimensioni;
- forma geometrica è quella di un cilindro di direttrice generica sufficientemente allungata;
- asse rettilineo;
- corpo costituito di materiale omogeneo, isotropo, linearmente elastico;
- corpo libero da vincoli esterni;
- sezione trasversale del corpo qualsiasi ma compatta e non dispersa;
•
per le forze esterna attive:
- forze applicate esclusivamente sulle superfici di base con distribuzione arbitraria;
- forze superficiali, quindi, nulle sulla superficie laterale che risulta scarica:
px = p y = pz = 0 ;
- forze di volume f x = f y = f z = 0 ovunque nel volume V;
- sistema equilibrato.
Sia il sistema di riferimento cartesiano x, y, z, ortonormale, con l'origine O nel baricentro
della sezione trasversale iniziale, l'asse z disposto secondo l'asse del cilindro, mentre gli
assi x e y coincidono con le direzioni principali d'inerzia [1] della sezione.
Sotto queste ipotesi si devono determinare lo stato di tensione, di deformazione e il campo
di spostamento della trave.
De Saint Venant ha per primo fornito una soluzione approssimata del problema
dell'equilibrio elastico del cilindro, poiché assume le azioni applicate sulle basi, definite
solo dalla risultante e dal momento risultante.
1.2 Il metodo semi-inverso
Il sistema di equazioni differenziali che regge il problema di De St. Venant presenta grosse
difficoltà analitiche se affrontato in piena generalità.
Come propose lo stesso De St. Venant si può ricorrere al così detto metodo semi - inverso;
il metodo consiste nel fissare a priori in modo arbitrario alcune caratteristiche della
soluzione, precisamente sono poste nulle tre componenti dello stato di tensione in ogni
punto della trave:
σ x = σ y = τ xy = 0
1)
Successivamente si determinano con le equazioni del problema elastico le altre componenti
di tensione, infine le condizioni al contorno definiscono le forze da applicare sulle basi per
ottenere quella soluzione.
Le 1) furono suggerite dall'intuito di De St. Venant, osservando la geometria del solido e la
modalità di applicazione delle forze.
La soluzione così trovata, quando non sorgono incompatibilità tra la scelta fatta a priori e
le equazioni da soddisfare, è proprio la soluzione cercata, per l'unicità della soluzione del
problema dell'equilibrio elastico.
Riassumendo si può dire che nel problema di De St. Venant
•
sono noti a priori:
- il dominio di definizione del problema;
- le forze di massa e le forze sulla superficie laterale;
- le caratteristiche del materiale ( E, G, ν, moduli tecnici del materiale)
- alcune componenti di tensione in ogni punto del corpo ( σ x = σ y = τ xy = 0 );
•
sono incognite:
- le componenti di tensione non nulle a priori;
- le componenti di deformazione in ogni punto del corpo;
- le componenti di spostamento in ogni punto del corpo;
- le distribuzioni delle forze sulle basi.
1.3 Il principio di De Saint Venant
Il problema di De St. Venant risolto assumendo le azioni sulle basi definite solo dalla
risultante a dal momento risultante, non considerando quindi i valori locali delle forze
applicate sulle basi, fornisce una soluzione meno difficoltosa, ma approssimata.
L'approssimazione di tali soluzioni è tuttavia legata alla validità di un principio ideato dallo
stesso De St. Venant.
Tale principio afferma che sostituendo ad un dato sistema di forze applicate alle basi del
cilindro un altro sistema ad esso staticamente equivalente, gli effetti della sollecitazione
non si sentono nei punti del solido situati a sufficiente distanza dalle basi; ciò equivale a
dire che la soluzione nella parte centrale della trave è invariante, e quindi che la differenza
tra le soluzioni, al variare della distribuzione delle forze di superficie applicate alle due
teste, a parità di risultante e momento risultante, è apprezzabile solo in prossimità delle
teste stesse delle travi.
Per questo motivo tra le ipotesi del problema di De St. Venant si trova che la geometria del
corpo solido deve essere sufficientemente allungata.
1.4 Le caratteristiche della sollecitazione
Le condizioni al contorno sulle basi z =0, z = l , portano ad identificare le forze di
superficie, su di esse applicate, con le componenti di tensione nei punti sulle basi, cioè:
τ zx = f x , τ zy = f y , σ z = f z .
2)
Le predette azioni agenti sulle basi, nella generica sezione trasversale di ascissa z,
definiscono le sei caratteristiche della sollecitazione, e precisamente:
- sforzo normale N
- tagli Tx , T y
- momenti flettenti M x , M y
- momento torcente M z ,
secondo la notazione e le convenzioni di segno, come riportato in figura 1.
figura1
Detta A l’area della sezione trasversale D, tenendo conto della 2), si hanno le seguenti
componenti della sollecitazione esterna:
ℑlx = ∫ f x dA = ∫ τ zx dA = Tx
D
D
ℑly = ∫ f y dA = ∫ τ zy dA = T y
D
3a)
D
ℑlz = ∫ f z dA = ∫ σ z dA = N
D
D
M xl = ∫ f z ydA = ∫ σ z ydA = M xl
D
D
M ly = ∫ f z xdA = − ∫ σ z xdA = M yl
D
3b)
D
M zl = ∫ ( f y x − f x y )dA = ∫ (τ zy x − τ zx )dA = M zl
D
D
Le componenti della risultante e del momento risultante delle tensione interne, rispetto al
un sistema di riferimento adottato, si chiamano parametri della sollecitazione.
Sulla sezione terminale della trave, in corrispondenza di z = l , i parametri della
sollecitazione sono definiti dalle 3a), 3b); su una sezione qualunque di normale uscente
equiversa con l’asse z, valgono le 3a), mentre per l’equilibrio alla rotazione intorno agli
assi si ha:
M x = M xl − T yl (l − z )
M y = M yl + Txl (l − z )
3c)
M z = M zl
Nel sistema di riferimento adottato, su una sezione di normale esterna discorde all’asse z, i
parametri di sollecitazione risultano invece, di segno contrario rispetto alle 3a) e alle 3c).
Sulla base in corrispondenza di z =0 le caratteristiche della sollecitazione esterna dettate
dalle condizioni di equilibrio del corpo rigido, risultano:
ℑ0x = −ℑlx
ℑ0y = −ℑly
3d)
ℑ0z = −ℑlz
M xl = −M xl + ℑly l
M ly = −M ly − ℑlx l
M zl = −M zl .
Queste condizioni sono rappresentate in figura 2
figura 2
3e)
1.5 Proprietà dello stato di tensione nella trave di De Saint Venant
Dalle condizioni 1) derivano alcune proprietà generali dello stato di tensione, valide per
qualunque sistema di forze applicate alle basi della trave al di fuori della zona di
estinzione.
Ci si limita in questo paragrafo, ad elencare tali proprietà, rimandando le dimostrazioni alla
letteratura consigliata per chi volesse approfondire l’argomento.
In riferimento al sistema di assi cartesiani secondo cui l’asse della trave è orientato lungo
l’asse z e le rispettive basi giacciono nel piano x,y come riportato in figura 3, si osserva
che:
figura 3
a) sulle giaciture parallele all’asse z la tensione è solo tangenziale di direzione z;
b) le componenti tangenziali della tensione sono indipendenti da z;
c) lo stato di tensione è biassiale;
d) il vettore tensione tangenziale totale è tangente al contorno
1.6 Soluzioni del problema di De Saint Venant
Si propone, essendo il corpo libero la soluzione del problema dell’equilibrio elastico [2],
secondo il metodo delle forze [3].
Ricordando che le incognite sono le componenti di tensione σ z ,τ zx e τ zy ,
- le equazioni indefinite di equilibrio, tenendo conto della 1), diventano:
 ∂τ zx
 ∂z = 0

 ∂τ zy
=0

∂
z

 ∂τ zx ∂τ yz ∂σ z
+
+
=0

∂y
∂z
 ∂x
4a )
4b)
4c)
e si può notare che la 1) implica che le tensioni tangenziali dipendono solo da x e da y;
- le equazioni di congruenza di Beltrami [4]:
per le ipotesi fatte sulle forze e sullo stato di tensione sono:
 ∂ 2σ z
 2 =0
 ∂x
 ∂ 2σ z
 2 =0
 ∂y
 2
∂ σ z = 0
 ∂z 2

 ∂σ z ∂σ z = 0
 ∂x ∂y
5a)
5b)
5c)
5d )
d’altra parte per le equazioni di equilibrio al contorno sulla superficie laterale ove σ z = 0
si ha, per le ipotesi 1), la condizione:
τ zxσ x + τ yzσ y = 0
6a)
mentre sulle basi, dove σ x = σ y = 0, σ z = 1 si ha:
τ zx = f x
τ zy = f y
6 c)
σ z = fz
6d)
6 b)
le 5) implicano che la componente σ z sia del tipo:
σ z = a + bx + cy − z (a1 + b1 x + c1 y )
7)
Le due equazioni rimanenti, tenendo conto della 7), si scrivono nella forma
∂ 2τ zx ∂ 2τ zx
1
b1
+
=
2
2
1 +ν
∂x
∂y
∂ 2τ zy
∂x
+
2
∂ 2τ zy
∂y
2
=
8a )
1
c1
1 +ν
8b)
Il problema si riduce quindi a tre equazioni differenziali, la 4c) e le 8a),8b).
Di queste la σ z dipende da sei costanti, mentre le τ zx , τ zy dipendono anche dal tipo di
materiale.
Tralasciando in questa trattazione i passaggi dimostrativi, rimandati ai testi consigliati [5],
si trova che il problema di De Saint-Venant è riconducibile alla determinazione di una
funzione armonica ϑ(x,y) nel dominio piano D coincidente con la sezione retta del cilindro
essendo prescritta la derivata di ϑ rispetto alla normale del contorno.
Si tratta quindi di risolvere un problema di Dini-Neumann la cui soluzione esiste unica a
meno di una costante additiva se:
∫
C
∂ϑ
ds = 0
∂n
9)
con C= contorno della sezione.
Per comodità di forma il problema generale di De Saint-Venant può essere suddiviso in tre
problemi parziali di Dini descritti dalle funzioni armoniche ϑ1 ,ϑ 2 ,ϑ0 ,
La 9) è ancora condizione necessaria e sufficiente perché il problema sia risolvibile dal
momento che è sempre soddisfatta.
In conclusione, la soluzione generale del problema di De Saint-Venant in termini di
tensione risulta:
σ z = a + bx + cy − z (b1 x + c1 y )
10a)
τ zx =
∂ϑ
∂ϑ1
∂ϑ
1 

2
) + c1 (2νxy − 2 ) + c0 ( 0 − y )
b1 ( x −
2(1 + ν ) 
∂x
∂x
∂x

10b)
τ zx =
∂ϑ

∂ϑ1
∂ϑ
1 
) + c1 ( y 2 − 2 ) + c 0 ( 0 + x)
b1 (2νxy −
2(1 + ν ) 
∂y
∂y
∂y

10c) .
- Costanti della soluzione:
risolto il problema di Dini, restano da determinare le sei costanti che compaiono nelle 10)
per definire lo stato di tensione in ogni punto del corpo.
Dalle condizioni di equivalenza meccanica tra le azioni interne e forze applicate sulla base
terminale del cilindro, in applicazione del principio di De Saint-Venant si individuano sei
casi di sollecitazione collegati con le seguenti costanti di integrazione:
sforzo normale
N Nl N0
a=
=
=
A
A
A
M y0
flessione con asse-momento y
b=
flessione con asse-momento x
M xl + T yl l
M x0
c=
=−
Ix
Ix
13)
taglio di direzione x
b1 = −
Tx
Tl
=− x
Iy
Iy
14)
Iy
Ty
taglio di direzione y
c1 = −
torsione pura
c0 = M t
Ix
=−
M yl + Txl l
11)
=−
Iy
T yl
Ix
12)
15)
16)
Questi casi, di cui solo quattro di essi sono effettivamente distinti, si riferiscono a
sollecitazioni semplici e corrispondono ad una sola costante di integrazione non nulla.
La scelta opportuna del sistema di riferimento per cui gli assi x e y sono principali
d’inerzia della sezione, ha portato ad una soluzione semplificata.