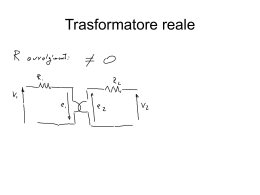
Trasformatore monofase
Trasformatore ideale
Il trasformatore ideale è un sistema lineare e non dissipativo
Ipotesi:
• Pfe = 0
• ρcu = 0 (Pcu=0)
• μfe =∞
η=1
u1i1=u2i2
Trasformatore monofase
ℜ fe
f =
1 l
=0
μ fe S
Tutto il flusso viene incanalato nel nucleo che si comporta come un unico tubo di flusso
(φ11=φ12 e φ22=φ21).
Si assume per il primario la convenzione di segno dell’utilizzatore e per il secondario quella
del generatore.
Definito
D
fi it il verso positivo
iti
del
d l flusso
fl
di mutua,
t
sii assume che
h i versii degli
d li avvolgimenti
l i
ti siano
i
tali che una corrente i1 positiva dia luogo ad un flusso autoconcatenato φ11 positivo (stesso
verso del flusso di mutua φ) e che una corrente i2 positiva dia luogo ad un flusso
autoconcatenato φ22 negativo (verso opposto rispetto al flusso di mutua φ).
Trasformatore monofase
Nei due avvolgimenti alimentati singolarmente sono indotte le tensioni:
|e11| = N1 dφ11/dt
|e22| = N2 dφ22/dt
I segni delle due forze elettromotrici indotte devono essere scelti in accordo con la Legge di
Lenz. Quindi, un incremento della corrente i1 (i2) e quindi del flusso φ11 (φ22) deve creare una
fem indotta e11 (e22) che si opponga all’incremento di i1 (i2). Si ha quindi:
e11 = N1 dφ11/dt
e22 = - N2 dφ22/dt
Per le assunzioni fatte sui segni dei flussi, le forze elettromotrici indotte dal flusso di mutua
valgono:
e1 = N1 dφ/dt
e2 = N2 dφ/dt
Trasformatore monofase
Per la legge di Faraday-Lenz
dφ
⎧
u
e
N
=
=
1
1
⎪⎪ 1
dt
⎨
⎪u = e = N dφ
2
2
⎪⎩ 2
dt
u1 e1
N
=
= 1 =t
u 2 e2 N2
= Rapporto spire
P1 = P2
Per la legge di Hopkinson
(o della circuitazione magnetica)
0 = ℜ fe φ = N1 i 1 − N 2 i 2
i1 N2
=
= 1/t
i2 N1
Trasformatore monofase
Funzionamento in regime sinusoidale
E1 M
ω
2 πf
⎧
E
=
=
N
Φ
=
N1Φ M = 4.44 N1Φ M
1
eff
ff
1
M
⎪⎪
2
2
2
⎨
E
2 πf
ω
⎪E
N 2Φ M =
N 2Φ M = 4.44 N 2Φ M
= 2M =
2
eff
⎪⎩
2
2
2
0 = ℜfeΦ = N1I1 − N2 I2
I1 N2
=
I2
N1
E1eff
N
= 1
E 2 eff N2
Trasformatore monofase
Trasformatore reale
perdite nei due avvolgimenti
g
(perdite nel rame)) e nel nucleo (perdite
(p
(p
nel
Tenendo conto delle p
ferro) si passa da un sistema ideale con rendimento unitario ad un sistema con rendimento
inferiore a uno.
Trasformatore monofase
Trasformatore con conduttori reali ( ρcu>0)
Le perdite negli avvolgimenti sono date dalla somma delle perdite in continua e delle perdite
addizionali. Queste ultime sono dovute all’incremento della resistenza degli avvolgimenti
passando dalla corrente continua alla corrente alternata, e sono causate dalla disuniforme
distribuzione delle correnti nei conduttori intersecati dai flussi dispersi.
Si tiene conto delle p
perdite nel rame,, e delle conseguenti
g
cadute di tensione,, inserendo nel
circuito equivalente due resistenze in serie agli avvolgimenti del trasformatore ideale, dette
rispettivamente resistenza di primario R1 e resistenza di secondario R2. Si ha:
R1 = (Pcu1+Padd1)/I12 ≠ RDC1
R2 = (Pcu2+Padd2)I22 ≠ RDC2
R1 ed R2 sono poste in serie agli avvolgimenti del trasformatore ideale perché in tal modo le
potenze dissipate nelle due resistenze sono proporzionali ai quadrati delle correnti di
primario e di secondario, come avviene nella realtà.
In fase di progetto R1, R2 vengono proporzionate in modo che i due avvolgimenti presentino
la stessa densità di corrente (nei trasformatori trifase di media e grande potenza 2,5÷ 3,5
[A/mm2] per il rame, 1,5 ÷ 2 [A/mm2] per l'alluminio, nei piccoli trasformatori monofase 1,5 ÷
2,4 [A/mm2] decrescente all'aumentare della potenza per il rame).
Trasformatore monofase
Circuito equivalente del trasformatore con conduttori reali
Si ha:
V1 E1 N1
≠
=
V2 E 2 N2
V1I1 ≠ V2 I2
0 = ℜφ = N1I1 − N2 I2
I1 N2
=
I 2 N1
Trasformatore monofase
Trasformatore con nucleo ferromagnetico reale
In un nucleo ferromagnetico reale la permeabilità magnetica non è infinita, si verifica il
fenomeno della saturazione magnetica ed infine sono presenti perdite di potenza per isteresi
e correnti parassite.
Effetti della permeabilità magnetica finita
Si ha: μfe ≠∞
(μfe = μr μo
μr = 7000 ; μo = 1,26 10-6)
Corrente di magnetizzazione ≠ 0
La riluttanza del nucleo vale: ℜ fe =
1 l
≠0
μfe S
Flussi di dispersione ≠ 0
Trasformatore monofase
Se μfe ≠∞ si ha:
ℜ fe =
1 l
≠0
μfe S
Per la legge di Hopkinson:
ℜ feφ = Fmm
A vuoto ( I1 = I10 ; I 2 =0) si ha:
ℜfeφ = N1I10
I10 =
A carico ( I 2 ≠0) si ha:
ℜ feφ = N1 I1 − N2 I 2
I1 =
ℜ feφ
N1
ℜ feφ + N 2 I 2
N1
Trasformatore monofase
In un trasformatore reale la corrente di primario, non dipende solo dalla corrente di
secondario, come nel trasformatore ideale, ma anche dal flusso, poiché il flusso deve essere
sostenuto da una componente di corrente detta corrente di magnetizzazione.
In particolare, a vuoto si ha:
I10 =
ℜ feφ
= I1m
N1
A carico si ha invece:
I1 =
ℜ feφ N 2 I 2
N I
+
= I 1m + 2 2
N1
N1
N1
A differenza del trasformatore ideale, quindi:
I1 N2
≠
I2
N1
Trasformatore monofase
Trascurando le perdite nel ferro, la corrente di magnetizzazione coincide con la corrente
assorbita a vuoto dal trasformatore, scorre quindi anche quando I 2 =0, inoltre poiché:
NI
Φ = 1 1m
ℜ
N12
E1 = jωN1Φ = jω
I1m = jX 1m I1m
ℜ
X 1m
N12
=ω
ℜ
per tener
t
conto
t d
della
ll corrente
t di magnetizzazione
ti
i
sii inserisce
i
i
in
i parallelo
ll l all primario
i
i del
d l
trasformatore ideale una reattanza induttiva X1m (o X’0) detta reattanza di magnetizzazione.
Si ha quindi:
⎧E1 = jω λ1 = jω N1Φ = jX 1 m I1 m
⎪
N2
⎨
⎪E 2 = jω λ 2 = jω N 2Φ = jω N 2Φ = j N X 1 m I1 m
⎩
1
L’introduzione della reattanza di magnetizzazione permette di considerare il flusso φ come
sostenuto solo dalla corrente che scorre nell’avvolgimento primario. In alternativa, come già
visto
i t nell caso di due
d
avvolgimenti
l i
ti accoppiati,
i ti è possibile
ibil fare
f
un ragionamento
i
t duale
d l ed
d
introdurre in maniera equivalente una reattanza di magnetizzazione X2m (o X”0) in parallelo al
secondario, precorsa dalla corrente di magnetizzazione riportata al secondario.