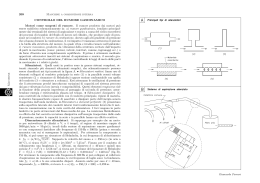
Ewm pio n. 4 - I I rimnutore dielettrico.
Wn risonatorc dicklrrico pub cssere
ottmvto
facendo risonare una guida dielemica di
opporhlna lungheua c opporhmamentc t m i n a t a agli esmmi.
NelIe applicazioni le guide dieIettriche. usate come risonatoti, sone insmite spesso in
tubi circolari o rettangolari metallici per consentirc uno schcrmaggio del risonatore e una
lirnilazione deHa regrone di spazio in cui k racchiusa I'cncrgia elctlrornagncLica per evitare
sia inkrazioni con gli aggctti circostanti che irradiazioni (vedi esempi in fig. 3.51).
-
F ~ R U3.51
F ~ Esempl di risottotori dicktteci iiuerili in tubi metallici: oJrisonatorc dielettrico
cir'indrico circolartz inrerito assialmente in una guidu rnetollico circolure; b) rimnature dieIerlrico cilindrico ciscolore inserito in m guida rnerallica a ssaione ~tlnangolareo quadrara
con I'asse del cilindro parallcio a un loto della sezione d~ f l guida:
a
c) sisunatom dieleltrico
a sezione scrfangolore,inseriro in urn g u m metaIlico rerrango[are.
Ln detmminazionc delle dirnmsioni o delle frequenze di risonan?~di un risonamre diclcttrico cilindrico di Iunghezza I, di mggio r = R e costante dielctrrica relativa E,, pasto in una
guida d'onda reltangolare di lati a c b (wedi fig. 3.52) operantc sotto la fsequen7n di taglio
del suo modo EondarncntaIe T E l b . & smta nflmnrata in modo sola approssirnam. Vari liveEli
di approssirnazione sono stati finom proposti in lettenturn, da quella pih semplice rli Coha,
proposte sin dal 1968 (603, ad alrri v i a ria pih complessi.
Ncl mctodo di Cohn si ipohzxa che il risonatorc diclclhrlco. di fomn ciIindrica circolate di
raggio R, di lunghez~aI e costantc dielettrica c,, p t o tr;l due piani mctdlici parallcli. distanti
a (fig. 3.52). orzo~onaliall'asse del cilindm, d comporti in prima appmssimaxionc come una
guidn d'onda circolarc a pmtc magnelocondultrice. rjcmpita dell0 stesso diclctt~ico,di nggio
R e lunghcma I. tcminata su duc guidc circalari dctlo slcsso ramie, ma vuou: o rlcmpitc di
due dicbtrrici divcrsi ( E , ~e E , ~ )dj v a l m talc che dcflc guide opcrino som la lorn f q u c n z a
di taglio. Dcttc guidc sono cortucircuimtc ai Ioro esmmi c di lungheva ris~ttivamenteII e
i2,
tali da risuItarc ovviamente:
a=11+I+12.
[3.107]
Figura 3.52 - Struttwa tipica di risonatore dielettrico cilindrico di diametro D e lunghezza
1, inserito in una guida rettangolare (tipicamente le dimensioni a e b sono poco diverse).
Lo schema del modello di Cohn del risonatore dieletttico b pertanto quello di fig. 3.53,
p b la costante di fase e Z , b l'impedenza caratteristica del tratto 1 in propagazione,
a 1 e a 2 sono le costanti di attenuazione dei due tratti sotto il taglio e ZC1e ZC2le rispettive
impedenze caratteristiche.
in cui
I
-
Figura 3.53 Schema del risonatore dielettrico nel modello di Cohn e in quello di Itoh,
come linea di trasmissione risonante lunga 1 di impedenza caratteristica Z , e costante di fase
p, chiusa su due tratti ll e l2 di linee sotto il taglio di costante di attenuazione cul e a2 e
impedenza caratteristica ZC1e Ze2.
I1 modo di propagazione che si considera b il modo T E o l , la cui prima risonanza viene
indicata come T E o l a ,essendo 67r = Dl la lunghezza elettrica del risonatore dielettrico con
6 < 1. Risulta ovviarnente 6 = 1 nel caso limite di ll = I2 = 0.
a lunghezza 1 pub essere valutata osservando che all'intemo del tratto 1 esiste un venue
~sione,che comsponde a un circuit0 aperto, che divide il tratto 1 in due tratti di lunghezra
rispettiva I' e 1''. Imponendo separatamente la condizione di risonanza di ciascun tratto con
la reatlanza corrispondente terminale, costituita dai tratti lI e l2 operanti sotto il taglio si
ottengono le due equazioni:
Se Po b la costante di fase dello spazio libero e k E l'autovalore dell'equazione di Helmhola
per il modo considerato TEol della guida d'onda, i valori di a , , cr2 e P risultano i seguenti:
e i valori di Z,, ZC1e ZC2, potendosi assumere eguali alle rispettive impedenze d'onda,
essendo omogenee le tre guide e di egual diametro, risultano i seguenti:
I1 valore dell'autovalore k del modo TEol corrisponde a1 primo zero dell'equazione (dove
si C posto x = kR):
Jol(x) = 0
[3.111]
e vale x = kR r 2,40482. Si ha pertanto (ponendo n = 1 nel caso della prima risonanza
del mod0 TEol):
I
[b
I
tanh(crlll) - arctan - tanh(cr212) .
Essendo assegnati nel caso di progetto la frequenza di risonanza, il lato a e il raggio R,
la lunghezza 1 pub essere determinata per successive approssimazioni in modo da soddisfare
la relazione [3.112]. Un primo valore approssimato pub essere Wvato ponendo nella [3.112]
ll = l2 = m, che P abbastan~abcn verificata se b a molto grande rispetto a I. Se & lI = l2
la [3.112] si semplifica ponendo in essa ll = l2 = (I - a)/2.
Nel caso di progetto occorre pertanto definire preliminarmente a e il diametro 2R del
dielenrico. I1 lato a va scelto in modo che la guida rettangolare open decisamente sotto la
frequenza di taglio nclla banda desiderata di funzionamento del risonatore, ma sufficientemente pic pande rispetto alla lunghezza 1, che risultera per il dielettrico.
Detta quindi A, la lunghem d'onda nello spazio libero corrispondente alla frequenza di
risonanza del risonatore, deve essere:
Per quanto riguarda la scelta preliminare del diametro D = 2R, si pub oesservare che E
opportune che il cilindro dieletfrico abbia un rappono .'ID prossirno a 0.4 per distanziare
maggiormente le risonanze indesiderate.
Quando invece sono assegnate tutte le dimensioni e si vuole ca\colare la frequenza di
risonanza il problema t pih complesso perch6 la frequenza compare sia nella costante di fase
p che nelle costanti di attenuazione a1 e cu2, che compaiono c i d sia a primo membro che a
second0 rnembro nell'equazione [3.112] che va risolta quindi per successive approssimazioni
a partire da un valore approssimato della frequenza.
Si noti che la lunghezza 1 del risonatore risulta sempre pih corta di mezza lunghezza
d'onda nella guida circolare con dielettrico e coincide con tale valore solo quando 1 = a.
Se si diminuisce a pertanto in mod0 da farlo tendere a I, la lunghezza del risonatore cresce
tendendo a A,/2 (nel dielettrico).
risonatore dielettrico
Figura 3.54 - Andamenfo della lunghezza normalizzafa !/An di un risonatore dielerrrico in
fmzione &l diamefro normalizzato D/Ad, per l 1 /Ad = 0 , 0,02, 0 , 1 calcolafo con il metodo si
Cohn, con quello di Ifoh-Rudokas e con qucllo di Kafez, per una costanre dieleffricaE , = 36
eper c r l = cr2 = 1 .
In fig. 3.54 si riporta l'andamento della lunghezza normalizmla del risonatore [/Ad, dove
Ad & la lunghezza d'onda propria del dielettrico (Ad = A/&)
in funzione del diametro
normalizmto del dialettrico D/Ad, per vari valori normalizirati alla lunghezza d'onda X nello
spazio libero di /,/A = 12/A. Le curve sono tracciatc per E , = 36, ma finch6 E , C sufficientemente grande (> 20), le curve cosl normalizirate variano pochissimo al variare di
Er.
Si noti che poicht il modello di Cohn trascura l'energia a1 di fuori del dielettrico, che
t principalmente di t i p magnetico, esso porta ad un errore della frequenza di risonanza (e
quindi della lunghezza nel caso di progetto per un diametro assegnato) che C in difetto rispetto
a quella reale.
I1 metodo di Itoh e Rudokas ( 6 1 ) modifica il metodo di Cohn, solo per il fatto che
considera il tratto in propagazione dello schema di fig. 3.53 costituito da una guida dieletaica
nello spazio libero anziche da una guida d'onda con parete magnetoconduttrice. Ne consegue
certamente una migliore approssirnazione, in quanto si tiene conto anche del campo estemo
al dielettrico. Cib peraltro viene effettuato in maniera solo approssimata, poichC non si tiene
conto nB degli effetti della presenza delle pareti metalliche della guida rettangolare parallele
all'asse del cilindro dielettrico, nC in mod0 corretto di quelli del troncamento di questo
cilindro.
Anche il modello di Itoh e Rudokas termina la guida dielettrica su due guide d'onda cilindriche sotto il taglio come il modello di Cohn, ma ipotizzando una distribuzione radiale
approssimata del c a m p in esse eguale a quella della guida dielettrica. L'errore che si commette con questo modello C peraltro ancora elevato e conduce ad una lunghezza o ad una
frequenza di risonanza superiori a quella reale.
Nel caso di progetto del risonatore k assegnata la frequenza di risonanza e le [2.105] e
[2.130] di Tab. 2.11 insieme alla condizione di risonanza, che C ancora data dalla E3.1121,
permettono di ricavare le dimensioni del cilindro dielettrico.
Conviene anche in questo caso assegnare il diametro del cilindro e ricavare dalle equazioni
citate la lunghezza 1 del cilindro dielettrico. Assegnato infatti il diarnetro 2 R dalla [2.105] si
ricava y in funzione di x e quindi dalla [2.130] si ricava x e ciok l'autovalore.
Si noti che il primo valore di x che risolve la [2.130], essendo le funzioni di Bessel
sempre positive, deve essere compreso Ira x = 2,40482 e x = 3,83171.
modificate, I<,-, e
Determinato x le [3.1091 e [3.1101 consentono di determinare c u l , cu2, P , Z c , Z c l e Zcz e la
[3.112] determina ancora I .
In tale valutazione occorre scegliere anzitutto il valore da assegnare al diametro del cilindro
D = 2 R . Si pub anche questa volta osservare che in questo caso, sempre per un rapport0
I / D prossimo a 0.4, vale la seguente relazione approssimata tra il prodotto della lunghezza
normalizzata l/Xd e del quadrat0 del diametro, pure normalizzato a Ad, se la distanza delle
pareti laterali della guida k sufficientemente grande e E , >> 1:
lD2/Xi Z 0,64 .
Si pub pertanto in prima approssimazione assumere per 2 R un valore eguale o prossimo
a 2 R 2 1,26Ad.
La precisione del modello di Itoh e Rudokas pub perb ancora essere migliorata introducendo una correzione variazionale della lunghezza o della frequenza di risonanza ( 6 2 ) .
Una semplificazione analitica del calcolo del risonatore dieletrico con il modello di Itoh
e Rudokas t stata suggerita da Kaifez ( 6 3 ) . Essa C di un certo interesse pratico, oltre che
per la maggiore semplicita di calcolo, anche perch6 I'errore generato dalle semplificazioni di
calcolo invodotte porta a risultati calcolati per le dimensioni o la frequenza di risonanza del
risonatore pih precisi del metodo originale di Itoh e Rudokas e pih vicini a quelli ottenuti con
la correzione variazionale per un'ampia gamma di distanze dalle pareti laterali della guida
d'onda di schermo.
Si C osservato che IB soluzione della equazione [2.130] t tra x = 2,40482 e x = 3,83171.
In tale intervallo il rapporto tra Jo e J1 pub essere approssimato come:
e il rapporto tra Iio e K1, nell'intervallo della variabile y tra 2 e 10 come:
La [2.130] ammette come soluzione del primo ordine:
con:
yo = J ( p o ~ ) 2 ( E r - 1 ) - 2,4052 .
Noto x il calcolo della lunghezza del risonatore procede come nel metodo di Itoh e
Rudokas.
Sono stati proposti anche vari modelli di calcolo piG complessi di quelli sopra
ricordati.
Tra di essi il metodo del "mode matching" sembra quello piii generale e preciso,
almeno per strutture, costituite da risonatori dielettrici cilindrici inseriti in guide circolari metalliche, alle quali pib essere ricondotto anche il caso di risonatori dielettrici
inseriti in guide rettangolari (fig. 3-52), se le pareti della guida, parallele all'asse del
cilindro dielettrico sono sufficientemente lontane dalla superficie del dielettrico.
Tali metodi richiedono calcoli molto complessi e l'intervento di elaboratori potenti. Richiedono inoltre la conoscenza preliminare abbastanza approssimata della
frequenza di
a, essendo metodi di analisi di strutture di dimensic