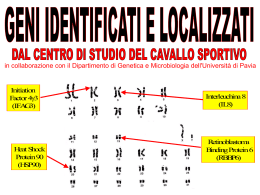
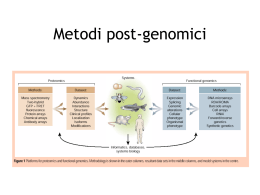
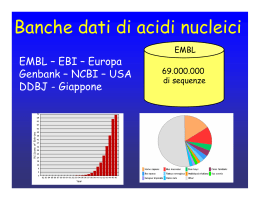
Interazione luce-materia
Assorbimento
Emissione (spontanea stimolata)
Processi “lineari”
Diffusione (elastica - inelastica)
Processi “a più fotoni”
(Assorbimento a due - tre
fotoni, generazione di seconda
armonica, oscillatori
parametrici, CARS, ecc...)
Processi “non-lineari”
Espansioni in serie
Serie di Taylor
Esempio: potenziale vicino ad un minimo
Approssimazione “armonica”
V(x) = V0 + kx2 + ax3 + bx4 + ...
Biological Application of Fluorescence
•genome sequencing
•real-time PCR
•DNA arrays
•protein arrays
•protein interactions
•protein expression profile
•In-situ hybridization
•protein localization
•protein movement
•Protein-DNA
•Protein-drug
•DNA-drug
Ripasso
Soluzioni dell’equazione di Schrödinger indipendente dal tempo:
ψn
base “ortonormale”:
ψ i ψ k = δ ik
1, i = k
δ ik = 
0, i ≠ k
Rappresentazione nello spazio degli autostati di H0:
an = ψ n ψ
Considero una perturbazione:
Scrivo la soluzione nella rappresentazione delle
coordinate nella base degli autostati di H0:
Sostituisco nell’equazione di Schrödinger completa
dipendente dal tempo:
Moltiplico per
ψk a destra e sinistra, integro su x:
ωkn=(Ek-En)/ħ
Teoria delle perturbazioni
dipendente dal tempo:
Ordine 1:
Caso particolare:
perturbazione sinusoidale su un autostato
Serie - Integrale di Fourier
1
1
0.8
0.6
0.8
∆t
∆ω~1/∆t
0.4
0.6
0.4
0.2
0.2
-15
-2
-1
1
-10
2
Delta di Dirac
=0 x≠0
5
-5
-0.2
10
15
 sin[(ωmn ± ω )t / 2]
 ~ 2π ψ m W ψ n

 (ωmn ± ω ) / 2 
2
P(m|t) =
|am(t)|2
~ ψm W ψn
2
Regola d’oro di Fermi
2
tδ (ωmn ± ω )
 sin[(ωmn ± ω )t / 2]


ω
ω
(
)
/
2
±
mn


∆ω=4π/t
Integrale = 2πt
2
max=t2/4
 sin[(ωmn ± ω )t / 2]


(
ω
ω
)
/
2
±
mn


2
2πtδ (ωmn ± ω ) (t → ∞)
types of bond important in biomolecules:
σ (sigma)
π (pi)
n (non-bonding)
excited
states
ground
state