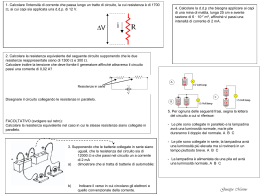
Raccolta di esercizi di elettronica
Esercitazione 1
1) Rappresentare analiticamente il segnale costituito da un impulso trapezoidale con fronte di salita
di 1 s e fronte di discesa di 4 s, che mantiene ampiezza costante di 2 volt per 5 s.
2) Calcolare le frequenze dei segnali armonici elementari presenti all’uscita del sistema governato
dall’equazione: y = x + ax2 quando il segnale d’ingresso è:
x(t) = cos(2 t) + cos(2 t).
3) Per un sistema governato dall’equazione y = x + ax3 vogliamo determinare sperimentalmente il
coefficiente a, che ne caratterizza la nonlinearità. Disponiamo di due generatori di segnali
sinusoidali con distorsione armonica incognita e di un analizzatore di frequenza. Descrivere una
strategia di misura, che sia veramente efficace.
4) Disegnare un circuito per misurare il guadagno in corrente di un transistore bipolare NPN,
utilizzando una batteria da 9 volt, un amperometro con portata di 1 mA e resistori a scelta.
5) Valutare approssimativamente la quantità d’informazione, in unità di bit, necessaria per
rappresentare tre minuti di musica.
Esercitazione 2
1) Determinare il fattore di picco (rapporto fra il valor massimo e la deviazione standard) della
somma di n = 1, 2, 3, 4, 5 segnali casuali, indipendenti fra loro, aventi distribuzione uniforme
nell’intervallo (-0,5, 0,5). Ricordiamo che la funzione densità della somma di due segnali casuali
indipendenti è la convoluzione delle densità dei segnali e che la varianza della somma è la somma
delle varianze degli addendi.
2) Ci serve una tensione di circa 1,5 V. Nel cassetto troviamo una batteria da 9 volt, un
condensatore da 10 nF, due resistori da 10 k, tre da 1 k, quattro diodi al silicio e una lampadina.
Che facciamo?
3) A un circuito RC passabasso con = 1 s è applicato un ingresso costituito da tre impulsi
rettangolari di durata 0,25 s; il primo con ampiezza 1 V e inizio al tempo 0, il secondo con
ampiezza –2 V al tempo t = 1 s, il terzo con ampiezza 3 V al tempo t = 3 s. Tracciare il grafico del
segnale d’uscita: a) ricavato in modo esatto, b) ricavato approssimando ciascun impulso mediante
una funzione delta (attenzione alla scelta del tempo di occorrenza delle funzioni delta).
4) Proporre una rappresentazione semplificata all’osso dell’eccitazione complessiva considerata
nel problema precedente, da utilizzare per il calcolo approssimato della risposta nel caso in cui il
circuito abbia costante di tempo di 100 s.
5) Si costruisce un cubo collegando 12 resistori da 1 ohm. Calcolare la resistenza a) fra gli estremi
di uno spigolo, b) fra i vertici opposti di una faccia, c) fra i vertici opposti del cubo.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
1
Esercitazione 3
1) Un amplificatore con resistenza d’uscita nulla alimenta con una tensione sinusoidale un resistore
di resistenza R = 8 ohm. L’uscita dell’amplificatore e’ soggetta alle seguenti limitazioni:
|i| minore o uguale a 0,1 A, |v| minore o uguale a 15 volt.
Individuare una soluzione che massimizzi la potenza erogata al carico (per segnale indistorto).
2) Graficare il modulo dell’impedenza in funzione della frequenza per un resistore di resistenza
= 100 ohm, con induttanza parassita L = 1 e capacità parassita C = 1 pF
R
3) Misurando con un ponte il parametro tangQ di un condensatore da 10 nF a varie frequenze,
si sono ottenuti i seguenti valori:
frequenza (kHz)
tang
(10-4)
0,1
11
0,2
5
1
1,2
2
0,8
10
2,2
20
4,1
100
21
Supponendo costante con la frequenza la capacità del condensatore, determinare, a ciascuna delle
frequenze in tabella, i valori della resistenza serie equivalente e della resistenza parallelo
equivalente. Usando questi risultati individuare un modello del condensatore reale, nel quale tutti gli
elementi, inclusi quelli parassiti siano rappresentati da parametri indipendenti dalla frequenza.
Eseguire infine un calcolo di verifica, confrontando i valori di tang ottenuti dal modello con quelli
in tabella.
4) Un condensatore di capacità C carico al potenziale V viene collegato mediante un interruttore a
un identico condensatore, inizialmente scarico. Assumendo che tutti gli elementi siano ideali,
calcolare la tensione assunta dai condensatori e l’energia del sistema, confrontandola con l’energia
iniziale. Discutere eventuali discrepanze fra quanto trovato e quanto aspettato. Discutere anche il
caso particolare in cui tutto il circuito sia costituito da metalli superconduttori e dunque presenti
resistenza elettrica nulla.
5) A un condensatore (reale) viene applicato l’impulso di corrente mostrato qui sotto, che sale in 10
ns da 0 a 1 mA,
i(t)
t
ottenendo la risposta in tensione (non in scala) mostrata sotto.
2 volt
0,1 volt
1,1 volt
1 microsecondo
t
Determinare, modellizzando il condensatore come un circuito RLC serie, la sua capacità C e i valori
dei parametri degli elementi parassiti R ed L.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
2
Esercitazione 4
1) La scatola A contiene un resistore R. La scatola B contiene la disposizione in parallelo di un
resistore R in serie a un induttore L,e di un altro resistore R in serie a un condensatore C.
Assumendo ideali i componenti, con R = 1 , L = 1 H e C = 1 F, stabilire se e’ possibile
distinguere le due scatole mediante misure elettriche.
R
L
R
C
R
A
B
2) Fra il l’ingresso di un amplificatore operazionale connesso come inseguitore di tensione (voltage
follower) e massa c’è la resistenza R. Questa è costituita da due resistori in serie, di resistenza R
quello collegato a massa e di resistenza (1-)R quello collegato all’ingresso dell’amplificatore. Il
terminale comune dei due resistori è collegato all’uscita dell’operazionale attraverso un
condensatore C.
a) Disegnare il circuito; b) Ricavare analiticamente l’espressione dell’impedenza d’ingresso del
circuito vista all’ingresso dell’operazionale, supponendo ideale il comportamento dell’operazionale,
e discuterne il significato; c) Calcolare numericamente questa impedenza ponendo R = 20 k e
C = 10 nF.
3) Calcolare la funzione di trasferimento del circuito
a fianco e studiarne in dettaglio l’andamento del modulo
(individuando eventuali massimi o minimi) e della fase
(individuando eventuali zeri).
4) Calcolare la funzione di trasferimento del circuito costituito da tre celle RC in cascata, con
resistenze R, R, 2R e capacità C, C/, C/2, individuando le differenze di comportamento fra il
caso = 1 e quello = 10. Progettare il circuito, scegliendo i valori di R, C e , quando lo si vuole
usare per filtrare il segnale proveniente da una sorgente di segnale con resistenza  10 ,
applicandolo a un convertitore A/D con resistenza d’ingresso  1M e frequenza di
campionamento di 1 kHz, in modo da garantire un’attenuazione  40 dB alla frequenza di Nyquist,
con errore in continua  3%.
5) Calcolare analiticamente e graficare la funzione descrittiva di un limitatore simmetrico con
ingresso x e uscita y (assumere y = -1 per x minore di –1; y = x per x compreso fra –1 e +1; y = 1
per x maggiore di 1.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
3
Esercitazione 5
1) Quando all’ingresso del circuito a fianco si applica
una tensione sinusoidale Vg, la tensione che si misura
fra i terminali A e B ha ampiezza pari alla metà di quella
del generatore, qualunque sia il valore del resistore R’
e la frequenza dell’onda di eccitazione. Individuare
il circuito all’interno della scatola, che può
comprende soltanto resistori e condensatori.
R
Vg
A
R’
B
scatola nera
2) Calcolare l’impedenza d’ingresso Z di una rete costituita da tre celle RC in cascata. Confrontare
il grafico del modulo di Z con quello del modulo dell’impedenza caratteristica di una linea RC
( Z '  1 sRC ). (Assumere, per semplicità: R = 1 ohm, C = 1 farad).
3) Un amplificatore operazionale con guadagno statico A0 di 100 dB ha tre poli reali (f1 = 10 Hz, f2
= 1 MHz, f3 = 2 MHz). Tracciare il grafico asintotico di Bode del modulo del guadagno. Calcolare
la frequenza di taglio a -3 dB. Trovare una espressione analitica, nell’approssimazione f2, f3 >> f1,
per la frequenza f180 a cui la fase della funzione di trasferimento assume il valore -.
4) Eseguendo misure della risposta in frequenza
di un circuito si sono ottenuti i risultati a fianco
(con la pulsazione w espressa in rad/s e la fase
in gradi). Individuare un modello matematico,
nella forma di una funzione di trasferimento,
che rappresenti ragionevolmente i dati.
w
modulo( w )
0.4
0.8
1.2
1.6
2
2.4
2.8
0.93
0.78
0.64
0.53
0.45
0.38
0.34
fase ( w )
45
84
119
150
178
205
231
5) Cinque celle RC identiche (RC = 1 ms), separate da amplificatori ideali a guadagno unitario,
sono collegate in cascata. Determinare alla svelta la forma della risposta a un gradino unitario ai
tempi brevi, immediatamente dopo l’applicazione del gradino.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
4
Esercitazione 6
1) Eseguendo misure su una bobina, eccitata con un generatore (Vo = 200 mV, Ro = 50 ohm) a varie
frequenze, si trovano i seguenti valori della tensione ai capi della bobina:
5 Hz
200 Hz
560 Hz
910 Hz
7 mV
37,8 mV
49,4 mV
70,5 mV
Scegliere un modello appropriato per la bobina in queste condizioni, determinarne i parametri ed
eseguire infine un calcolo di verifica.
(Attenzione: una delle misure potrebbe essere affetta da un forte errore).
2) Un defribillatore e’ costituito da un condensatore C = 32 F che viene scaricato, mediante un
interruttore, sul torace del paziente attraverso un induttore L = 35 mH e un resistore R = 67 .
Calcolare il fattore di merito e il coefficiente di smorzamento del circuito quando la resistenza
transtoracica del paziente assume i valori Rt = 20, 75 e 140 . Calcolate, nei tre casi, l’energia totale
somministrata al paziente quando l’energia iniziale del condensatore è 360 J.
3) Calcolare la funzione di trasferimento V2(s)/V1(s)
della rete a fianco (R = 1 k, C =1 nF), individuando la
posizione dei poli e degli zeri, e la risposta indiciale.
+
Graficare la risposta in frequenza (modulo e fase) e la
risposta indiciale.
V1(s)
_
R
C
+ V2(s) C
R
4) Dato il sistema con funzione di trasferimento H(s) = 1/(1+s)5, individuare dei modelli
approssimati (modello del primo ordine?, del secondo?, di altra natura?) per tale sistema, che ne
rappresentino efficacemente l’una o l’altra di proprietà, nel dominio del tempo o nel dominio della
frequenza, da voi giudicate interessanti (per esempio, ma non solo, il tempo di salita, il ritardo, la
banda a -3 dB, lo sfasamento, .......)
5 ) Un condensatore da 1 F ha i seguenti valori (reali e indipendenti dalla frequenza) dei parametri
parassiti: resistenza parallelo 100 Mresistenza serie 100 , induttanza serie 1 Tracciare il
grafico approssimato del modulo dell’impedenza in funzione della frequenza (scale logaritmiche) e
stabilite in quale regione tale oggetto si comporta decentemente come un condensatore.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
5
Esercitazione 7
1) Calcolare le costanti primarie di una linea non dispersiva, avente resistenza caratteristica di 50
ohm, capacità di 100 pF/metro e attenuazione di 0,1 dB/metro.
2) Ai due terminali di una scatola nera si applica una tensione a gradino di 1 volt attraverso un
resistore da 100 ohm. All’oscilloscopio si osserva un impulso rettangolare di ampiezza 0,333 volt e
durata 1 s. Stabilire il contenuto della scatola.
3) Una linea di trasmissione non dispersiva con resistenza caratteristica 50 ohm e lunghezza 100
metri (C = 100 pF/m) alimenta un carico di 100 ohm. Calcolare la forma d’onda della corrente
all’ingresso della linea e della tensione al carico quando la linea è eccitata da un generatore di
tensione a gradino di 1 volt e resistenza d’uscita di 50 ohm. Ripetere il calcolo nel caso in cui il
generatore di tensione sia ideale.
4) Calcolare la tensione, la resistenza differenziale r e il rapporto R = V/I di un diodo al silicio
(I0 = 10-10 A, = 2, Rohmica = 2 @ 300 K) per i seguenti valori di corrente: I = 1m
5) Progettare un semplice termometro usando i seguenti oggetti: due pile da 9 volt, un diodo a
giunzione, un amplificatore operazionale, resistori fissi e variabili a piacere.

6) Un diodo rivelatore, polarizzato inversamente, produce brevi impulsi di corrente, ciascuno con
carica totale di 10 pC. Questi vengono trasformati in segnali di tensione con un circuito costituito
solamente da un amplificatore invertente (con guadagno maggiore di 100) e un condensatore.
Individuare lo schema del circuito e scegliere un valore conveniente della capacità.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
6
Esercitazione 8
1) Un tester per corrente alternata, che utilizza un rettificatore a doppia semionda, è stato calibrato
per fornire il valore efficace di tensioni sinusoidali. Stabilire la lettura fornita dallo strumento
quando ad esso vengono applicati i seguenti segnali, tutti aventi valor medio nullo e valore di picco
di 10 volt:
a) un’onda sinusoidale; b) un’onda quadra; c) un’onda triangolare.
2) Si consideri una cella solare al silicio con i seguenti valori dei parametri: Io = 10-7 A, Rs=1 ,
=2, fotocorrente Is = 100 mA (in condizioni di illuminazione standard). Per un sistema costituito
da 10 celle disposte in serie determinare la tensione a vuoto, la resistenza ottimale di carico e la
massima potenza elettrica fornita al carico.
3) Un amplificatore a emettitore comune, previsto per transistori con  fra 50 e 200, è costituito da
un transistore NPN con emettitore a massa, e da un resistore di collettore (RC = 5 k) e un resistore
di base (RB = 500 k) collegati all’alimentatore (VCC = 10 V). Prima di montarlo, come lo
modifichereste (cambiando il valore di un solo componente)?
4) Calcolare i valori del parametro hie di un transistore bipolare a giunzione con hfe = 100 e
rbb’ = 200 ohm, assumendo  = 2, quando la corrente di collettore ha i seguenti valori:
1 10 mA.
Manca qualcosa per svolgerere il calcolo? Stabilitela voi.
5) Disegnare un semplice circuito per misurare la tensione Vz di un diodo zener.
Esercitazione 9
1) Un amplificatore a emettitore comune, alimentato a 12 volt, è costituito da un transistore (con
rbb’ = 100 ohm) e da quattro resistori aventi i seguenti valori: 1000 ohm, 12000 ohm, 47000 ohm,
4700 ohm. Individuare una ragionevole disposizione dei resistori. Calcolare quindi il guadagno di
tensione del circuito nel caso in cui si abbia hfe = 50 e hfe = 200.
2) Il circuito precedente viene comandato, attraverso un condensatore, da un segnale sinusoidale di
4 volt picco-picco. Ricavare e graficare la forma d’onda che si osserva in uscita.
3) Il circuito precedente viene comandato da un generatore attraverso un condensatore da 100 nF;
fra il collettore e massa viene disposto un condensatore da 220 pF. Assumendo hfe reale, calcolare la
funzione di trasferimento e tracciarne i diagrammi di Bode.
4) Modificare i valori dei componenti dell’amplificatore precedente in modo che possa essere
alimentato a batteria (6 volt) assorbendo a riposo una potenza non superiore a 0,6 mW.
5) Osservando all’oscilloscopio la tensione d’uscita di uno stadio
amplificatore a emettitore comune con resistore di emettitore comandato da
una sinusoide, si osserva la forma d’onda (periodica) mostrata in figura.
Spiegare perché.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
7
Esercitazione 10
1) Un impulso rettangolare positivo 0-10 volt con durata di 10 s è applicato all’ingresso di uno
stadio inseguitore d’emettitore dove in parallelo al resistore d’emettitore (1 k) si trova una
capacità di 2 nF. Disegnare approssimativamente la forma d’onda dell’impulso d’uscita
sull’emettitore e valutarne il tempo di discesa dandone interpretazione.
2) Calcolare l’impedenza per piccoli segnali offerta dalla rete a una porta rappresentata qui sotto,
ammettendo che il transistore JFET, convenientemente polarizzato, sia modellato da un generatore
ideale di corrente controllato in tensione: i2 = gm vgs, con gm = 10 mS. Individuare il comportamento
dell’impedenza nelle varie regioni di frequenza.
ii
i2
R =10 k
G
D
S
C =10 nF
3) Progettare uno stadio amplificatore a JFET con guadagno Av = -20, utilizzando un JFET a canale
N con IDSS = 10 mA, VP = -4 volt e rd = 20 k @ ID = IDSS.
4) Si vuole controreazionare un amplificatore con funzione di trasferimento
A(s) = A0/(1+1s)( 1+2s) con A0 = 100, s, s. Scegliere un opportuno valore reale
di , motivandolo brevemente.
5) Colleghiamo in cascata 3 stadi amplificatori identici ciascuno con guadagno A = 10 e costante di
tempo  = 1 s. Calcolare il guadagno, il tempo di salita e il ritardo del sistema così ottenuto. Che
succede se proviamo a controreazionare questo sistema? Per quale valore di  diventa un
oscillatore?
6) Considerare uno stadio amplificatore JFET a source comune, per cui s’imponga VD = VDD/2 ma
si possa scegliere liberamente il valore del resistore di carico RD. Determinare le condizioni di
polarizzazione per cui il guadagno di tensione risulta massimo.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
8
Esercitazione 11
1) Un amplificatore è costituito da un generatore ideale di corrente, controllato dalla tensione
d’ingresso, che alimenta l’impedenza di carico costituita da un resistore R = 1000 ohm in parallelo a
una capacità C =100 pF (capacità non eliminabile).Vogliamo allargare la banda passante e
velocizzare la risposta indiciale dell’amplificatore disponendo una induttanza L in serie al resistore.
a) Calcolare, in funzione di L, la banda passante, il tempo di salita e il tempo di ritardo
dell’amplificatore. b) Scegliere il valore di L che si ritiene più opportuno, ragionando nel dominio
del tempo oppure della frequenza. c) Calcolare i valori numerici dei fattori di miglioramento delle
grandezze anzidette, che si ottengono con tale scelta.

2) Un amplificatore di potenza, descritto dalla legge vo = 100 sin (vin), alimenta un carico di
resistenza R = 10 . Calcolare la distorsione totale dell’uscita per un segnale d’ingresso
vin(t) = Vin sin(t) quando la potenza fornita al carico è 10 W e quando è 100 W.
3) Un generatore di onde quadre con tempo di salita di 20 ns eccita un circuito RC con costante di
tempo = 20 ns. Calcolare il tempo di salita del segnale d’uscita osservato usando un oscilloscopio
con banda di 20 MHz.
4) Un amplificatore, quando è collegato all’alimentazione, presenta una capacità d’ingresso molto
maggiore di quando non è alimentato. Spiegare perché.
5) Stimare il tempo necessario per misurare in regime sinusoidale a 0,1 Hz la risposta di un sistema
passabasso del primo ordine con frequenza di taglio di 0,01 Hz.
Esercitazione 12
1) Vogliamo misurare la risposta di un fotodiodo a un flusso luminoso variabile nel tempo usando
un amplificatore a controreazione con tensione d’uscita proporzionale al flusso luminoso. Quale
delle 4 configurazioni standard sceglieremo? Perché?
2) Calcolare e graficare in funzione della frequenza l’impedenza d’ingresso (sul terminale
d’ingresso invertente) di un amplificatore operazionale, avente guadagno interno di 105 in continua
con il primo polo corrispondente alla frequenza di 10 Hz, con un resistore da 100 k disposto in
retroazione fra l’uscita e l’ingresso invertente, e l’ingresso non invertente collegato a massa.
3) Calcolare la varianza e lo spettro del rumore di tensione ai capi di un condensatore di capacità
C = 1 nF, in parallelo al quale sono disposti due resistori, in serie fra loro: R1 = 10 kΩ a T1 = 3 K,
R2 = 100 Ω a T2 = 300 K.
4) Calcolare la temperatura equivalente della disposizione in serie di due resistori: R1 = 10 kΩ a
T1 = 3 K, R2 = 100 Ω a T2 = 300 K. Calcolare lo spettro del rumore di tensione ai capi di un
condensatore di capacità C = 1 nF disposto in parallelo ai due resistori.
5) Una sorgente resistiva a 290 K viene applicata all’ingresso di un amplificatore con rumore
Vn = 10 nV/Hz e In = 0,1 pA/Hz. Calcolare la resistenza Rs* che minimizza il fattore di rumore.
Calcolare il fattore di rumore e lo spettro totale del rumore in ingresso per Rs*/10, Rs* e 10 Rs*.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag.
9
Ricapitolazione 1
1) Un circuito RC, con funzione di trasferimento 1/(1+s) dove  = 1 μs, viene eccitato con un
impulso unitario (t). Un circuito CR, con funzione di trasferimento s/(1+s), viene eccitato con
un segnale a gradino u(t)/. I due segnali d’uscita sono applicati agli ingressi A e B di un
oscilloscopio che rappresenta la differenza A-B. Disegnare la forma d’onda che si osserva.
2) Progettare un amplificatore per segnali fra 10 Hz e 10 kHz con guadagno 100 a centro banda,
usando un amplificatore operazionale. Tracciare i diagrammi di Bode (modulo e fase) della risposta
in frequenza. Valutare il tempo di salita e il tempo di ritardo dell’amplificatore. Discutere la
possibilità di estendere a 1 MHz la frequenza di taglio superiore,
3) Tre celle RC identiche (RC = 1 s), separate da amplificatori ideali a guadagno unitario, sono
collegate in cascata. Calcolare la risposta indiciale del circuito, esaminarne l’andamento
approssimato ai tempi brevi e interpretare il risultato. Calcolare l’andamento asintotico ad alta
frequenza del modulo e della fase della risposta del circuito.
4) Progettare un attenuatore da 20 dB per un sistema adattato a 50 ohm.
5) Progettare una sonda attenuatrice 1:10 per un oscilloscopio avente resistenza d’ingresso di 1 M
e capacità d’ingresso di 10 pF sapendo che il cavo che collega la sonda all’oscilloscopio ha capacità
di 40 pF. Proporre una soluzione per il caso in cui quest’ultima capacità può variare fra 30 e 50 pF.
6) Collegando un cristallo di quarzo fra l’ingresso invertente di un amplificatore operazionale
controreazionato con un resistore e massa può darsi che s’inneschi un’oscillazione. Spiegare perché.
7) Una linea di trasmissione accessibile a un estremo risulta guasta. Descrivete quale misura
eseguireste per determinare a che distanza dalla porta d’ingresso si trova il guasto.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag. 10
Ricapitolazione 2
1) Calcolare la risposta indiciale di due circuiti RC disposti in cascata, ma disaccoppiati da un
amplificatore separatore di guadagno unitario, il primo con costante di tempo , il secondo con
costante di tempo . Calcolare il tempo di ritardo e il tempo di salita del circuito per = 2 e
= 10. Tracciare i diagrammi di Bode, modulo e fase, per = 10. Il diagramma di fase si può
determinare esaminando il diagramma del modulo?
2) Scegliere i valori di A e di , entrambi reali, per ottenere un amplificatore reazionato con
guadagno ingresso-uscita AF = 10 e fattore di reazione D = 10. Calcolare i valori dei vari segnali
(d’uscita Vo, di reazione Vf, d’errore Ve) quando all’ingresso si ha Vin = 1 volt. Calcolare la risposta
indiciale ingresso-uscita dell’amplificatore se il blocco A è un passabasso con costante di tempo
0,1 ms. Calcolare, in quest’ultimo caso, il valore dei segnali (Vo, Vf, Ve) al tempo 0+ per un
ingresso a gradino di ampiezza 1 volt.
3) Progettare un amplificatore ad emettitore comune con guadagno di circa 10, indicando i criteri
seguiti nelle varie scelte. Calcolare l’impedenza d’ingresso del circuito. Cosa si può fare per
aumentarla di un fattore apprezzabile?
4) Calcolare la temperatura equivalente della disposizione in parallelo di due resistori: R1 = 10 kΩ
a T1 = 3 K, R2 = 100 Ω a T2 = 300 K. Calcolare lo spettro del rumore di tensione ai capi di un
condensatore di capacità C = 1 nF disposto in parallelo ai due resistori.
5) Vogliamo controreazionare un amplificatore costituito da tre stadi invertenti identici. Decidete se
controreazionare tutto l’amplificatore o ciascuno stadio singolarmente e spiegare brevemente il
motivo della scelta.
6) Guardando all’oscilloscopio l’onda quadra prodotta da un buon generatore di segnali, troviamo,
dopo i fronti d’onda, un decadimento con costante di tempo di 160 ms. Interpretare l’osservazione.
7) Un partitore realizzato disponendo in serie un resistore da 1 MΩ e una da 1 kΩ funziona
correttamente a bassa frequenza, ma a frequenze più elevate la risposta tende ad aumentare.
Proporre una interpretazione di questa osservazione.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag. 11
Ricapitolazione 3
1) Un circuito RC, con funzione di trasferimento 1/(1+s) dove  = 2 s, viene eccitato con
l’impulso (t). Un circuito CR, con funzione di trasferimento s/(1+s), viene eccitato con il
gradino (1/e) u(t-). Calcolare le uscite dei due circuiti nel dominio del tempo. I due segnali d’uscita
sono applicati agli ingressi A e B di un oscilloscopio che rappresenta la differenza A-B. Disegnare
la forma d’onda che si osserva.
2) Un induttore L = 1 mH ha resistenza serie R = 10 ohm e capacità parassita C = 5 pF fra i suoi
terminali. Tracciare il grafico approssimato del modulo dell’impedenza in funzione della frequenza
(scale logaritmiche) e stabilite in quale regione di frequenza tale oggetto si comporta onestamente.
Esprimere il fattore di merito in termini di R, L e C; calcolarne il valore.
3) Calcolare la funzione di trasferimento di un circuito CR seguito da un circuito RC, non
disaccoppiato dal primo, entrambi con R = 1 k e C = 1 F. Tracciare i diagrammi di Bode del
modulo e della fase.
4) Si vuole realizzare un amplificatore video per segnali nella banda fra 100 Hz e 10 MHz (con uno
zero all’origine e due poli reali corrispondenti alle due frequenze di taglio). Scegliete i valori delle
due costanti di tempo. Valutare il tempo di salita e il ritardo dell’amplificatore e calcolarne la
risposta indiciale. Tracciare i diagrammi di Bode della risposta in frequenza, modulo e fase.
5) Spiegare brevemente il motivo principale del basso rendimento delle celle solari.
6) Calcolare lo spettro del rumore di tensione ai capi di un condensatore C = 10 nF che si trova in
parallelo a un resistore R = 10 k alla temperatura di 300 K. Calcolare il valore quadratico medio
della tensione di rumore e ripetere il calcolo nel caso R = 1 .
7) Elencare molto brevemente le differenze e le analogie più significative fra un transistore bipolare
(BJT) e uno unipolare (JFET).
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag. 12
Ricapitolazione 4
1) Tre celle RC identiche (RC = 1 s), separate da amplificatori ideali a guadagno unitario, sono
collegate in cascata. Calcolare la frequenza a cui la funzione di trasferimento del sistema diventa
reale, determinandone il segno e il valore del modulo a tale frequenza.
2) Un partitore capacitivo costituito da due condensatori con capacità C1 = 10 F e C2 = 90 F
viene collegato a un alimentatore con tensione V = 100 volt. Calcolare la tensione d’uscita del
partitore al tempo t = 0+ e al tempo infinito, sapendo che le resistenze di perdita in parallelo ai
condensatori valgono rispettivamente R1 = 10 MΩ e R2 = 90 MΩ.
3) Si vuole realizzare un oscillatore con un inseguitore di emettitore (A = 1-) e una rete RC
passiva. E’ possibile?
4) Abbiamo tre batterie d’auto da 12 volt con resistenza interna, rispettivamente, di 0,5, 0,2 e 0,1
. Rappresentatele con modelli adeguati, determinandone i parametri: a) quando sono disposte in
serie, b) quando sono disposte in parallelo. Calcolare la potenza che, nei due casi, le batterie
erogano a regime a un carico avente resistenza di 1 ohm e induttanza di 1 H.
5) Sottoponendo un transistore bipolare a un flusso di radiazioni per un certo tempo, questo subisce
un danno permanente dovuto alla riduzione della vita media dei portatori. Individuare il parametro
del dispositivo che maggiormente ne risente.
6) Calcolare analiticamente i tempi di ritardo e di salita di un circuito RC passabasso avente
costante di tempo di 1 secondo. Considerando sia le definizioni analitiche che quelle empiriche. Per
lo stesso circuito calcolare anche i tempi di assestamento con scarto compatibile con l’impiego di un
convertitore A/D a) da 10 bit, b) da 20 bit.
7) Descrivere brevemente un esperimento per misurare il rendimento energetico di una cella solare.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag. 13
Ricapitolazione 5
1) Consideriamo la corrente che passa nel motorino di avviamento (R = 0,1 , L = 1 H) di un’auto
quando viene collegato, con fili di resistenza trascurabile, a tre batterie da 12 volt disposte in
parallelo, con resistenza interna, rispettivamente, di 0,5, 0,2 e 0,1 . Stabilire il valore della
corrente all’istante iniziale di accensione, dopo un minuto che il motorino gira e dopo tre ore.
2) Due celle CR, con costanti di tempo rispettivamente 1 = 1 ms e 2 = 2 ms, sono disposte in
cascata (con amplificatore separatore a guadagno unitario). Calcolare e disegnare la risposta
indiciale del circuito, determinando in particolare il tempo di salita e la pendenza iniziale.
3) Scegliere il valore di A e di  (entrambi reali) per realizzare un amplificatore reazionato con
guadagno ingresso-uscita AF = 50 e fattore di reazione D = 100. Calcolare i valori statici dei vari
segnali (d’uscita Vo, di reazione Vf, d’errore Ve) quando il segnale d’ingresso Vin è 100 mV.
Ammettendo che il blocco A abbia un tempo di salita non nullo, calcolare il valore dei segnali (Vo,
Vf, Ve) al tempo 0+. Ammettendo che il blocco A abbia un polo reale con costante di tempo di 1 s,
calcolare la banda passante dell’amplificatore reazionato. Discutere cosa avviene se il blocco A ha
due poli reali coincidenti.
4) Un circuito RC, con funzione di trasferimento 1/(1+s), viene eccitato con un gradino unitario
u(t). Un circuito CR, con funzione di trasferimento s/(1+s), viene eccitato con una rampa unitaria
r(t) = t u(t). Calcolare le uscite dei due circuiti nel dominio del tempo. I due segnali d’uscita sono
applicati agli ingressi A e B di un oscilloscopio che rappresenta la differenza A-B. Disegnare la
forma d’onda che si osserva.
5) Spiegare brevemente perché la resistenza d’ingresso sulla base di un inseguitore di emettitore
(emitter follower) è pari all’incirca al prodotto della resistenza di carico (fra l’emettitore e massa)
per il guadagno in corrente (β) del transistore.
6) Disegnate il diagramma della fase della funzione exp(-s)/(1+s)3 per ω fra 0 e 6 rad/s. Calcolate il
valore della fase per ω = 6 rad/s.
7) Fra l’ingresso e l’uscita di un circuito inseguitore di tensione con guadagno ingresso-uscita di
0,99 si trova un resistore da 10 k. Calcolate la resistenza d’ingresso del circuito assumendo
infinita l’impedenza d’ingresso dell’amplificatore.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag. 14
Ricapitolazione 6
1) Abbiamo un oscilloscopio, con tempo di salita di 10 s (la funzione di trasferimento comprende
un solo polo reale), che non si può modificare. Per ottenere una risposta 10 volte più veloce, anche
se eventualmente a spese del guadagno, disponiamo una opportuna rete passiva in cascata
all’ingresso dello strumento. Progettare la rete in modo da ottenere quanto desiderato supponendo
infinita l’impedenza d’ingresso dell’oscilloscopio.
2) Il primo compito settimanale l’hanno svolto 30 studenti, il secondo 27. Valutare quanti lo
svolgeranno alla 11 settimana nelle due ipotesi a) di decadimento lineare, b) di decadimento
esponenziale.
3) Affrontare nuovamente l’esercizio 4-1 a pag. 3 dopo aver letto il capitolo IX.
4) Un circuito CR con costante di tempo = 100 s è eccitato da una rampa di pendenza 1 V/s
applicata al tempo t = 0. Calcolare e graficare la forma d’onda d’uscita. Ripetere il calcolo nel caso
in cui al circuito ne segua un altro identico, disaccoppiato dal primo con un amplificatore ideale a
guadagno unitario. Calcoare il valor massimo della risposta nei due casi.
5) Osserviamo mediante un oscilloscopio il tempo di salita di un circuito RC con R = 10 000 ohm e
C = 100 pF, trovando che vale 3 microsecondi. Interpretare il risultato.
6) Calcolare la funzione di trasferimento di un circuito RC seguito da un circuito CR, non
disaccoppiato dal primo, entrambi con RC=1 ms. Tracciare i diagrammi di Bode del modulo e della
fase. Tracciare i diagrammi di Bode della risposta in frequenza: modulo e fase.
7) Ci serve una tensione di circa 200250 mV. Nel cassetto troviamo una batteria da 9 volt, un
condensatore da 10 nF, due resistori da 10 k, tre da 100 , quattro diodi al silicio e un transistore
guasto. Che facciamo?
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag. 15
Ricapitolazione 7
1) Nell’AA 97-98 il numero degli studenti che hanno svolto le esercitazioni di Elettronica in sette
settimane successive è stato il seguente: 8, 10, 10, 8, 7, 7, 5. Assumendo che questi dati descrivano
la risposta indiciale di un sistema con uno zero nell’origine e due poli reali, e che il gradino sia stato
applicato una settimana prima dell’inizio della sequenza, stimare le due costanti di tempo del
sistema e proporne un’interpretazione. Utilizzando il modello, stabilire il numero di studenti che
consegneranno esercitazioni nelle tre settimane successive.
2) Vogliamo realizzare un amplificatore con guadagno |100| a centro banda, taglio inferiore a 100
Hz, taglio superiore a 10 kHz, usando un operazionale, due resistori e due condensatori. Disegnare
lo schema e calcolare i valori dei componenti. Graficare la risposta in frequenza: modulo e fase.
Esprimere un giudizio sulla possibilità di spostare a 1 MHz il taglio superiore.
3) Eccitando un circuito RC con un generatore di onde quadre avente tempo di salita di 20 ns, e
osservando la risposta con un oscilloscopio da 20 MHz, troviamo che il tempo di salita è di 40 ns.
Qual è il tempo di salita del circuito?
4) Discutere brevemente il comportamento di un derivatore realizzato con un amplificatore
oparazionele al crescere della frequenza.
5) Calcolate il tempo di ritardo (0-50%) di un circuito RC con frequenza di taglio di 100 kHz.
6) Un amplificatore con guadagno A0 = 100, uno zero all’origine, due poli corrispondenti alle
frequenze 100 Hz e 1 kHz, e distorsione dell’3% per tensione d’uscita di 5 volt efficaci, viene
controreazionato con β = 0,09. Come si modificano le sue caratteristiche?
7) Calcolare l’induttanza e la capacità di un circuito risonante parallelo per la ricezione di un
segnale a 5 MHz con larghezza di banda di 20 kHz. Il carico, in parallelo al risonatore, ha resistenza
di 50 k.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag. 16
Ricapitolazione 8
1) Avendo smantellato una centrale nucleare che produceva 1 GW di potenza elettrica con
continuità, vogliamo sostituirla con una centrale solare impiegante pannelli fotovoltaici con
rendimento del 15%, che produca in media la stessa potenza. Determinare l’area della superficie di
terreno necessaria. Valutare approssimativamente il sistema di accumulo necessario per
immagazzinare una quantità di energia pari al prodotto della potenza massima per 2 ore,
supponendo di usare batterie da 12 volt con capacità di 100 Ah.
2) Vogliamo realizzare un attenuatore variabile su comando elettrico (0-5 V) per piccoli segnali in
corrente alternata, usando un diodo a giunzione, un condensatore, un resistore fisso e uno variabile.
Disegnare lo schema di principio.
3) Un amplificatore audio ha uno zero all’origine, un polo reale corrispondente alla frequenza di
taglio inferiore e un altro polo reale corrispondente alla frequenza di taglio superiore, e guadagno 10
a centro banda. Scegliere valori sensati per le due frequenze anzidette. Valutare quindi il tempo di
salita e il ritardo dell’amplificatore, e calcolare e graficare la risposta indiciale. Graficare la risposta
in frequenza: modulo e fase.
4) Calcolare la variazione della velocità iniziale della risposta indiciale di un amplificatore (con un
polo reale, τ = 1 μs, e A = 100) quando viene controreazionato con fattore di reazione D = 10.
5) Progettare un amplificatore ad emettitore comune con guadagno di circa 10, indicando i criteri
seguiti nelle varie scelte. Calcolare l’impedenza d’ingresso (di che? di tutto il circuito, ovviamente).
Indicare cosa potreste fare per renderla più alta (di che? di quanto vi è venuto).
6) Viene costruito un amplificatore utilizzando un amplificatore operazionale in configurazione
invertente con resistore di ingresso Rs = 10 k e resistore di reazione RF = 1 M. L’operazionale
ha guadagno in continua di 105, resistenza d’ingresso di 1 M e frequenza di taglio di 10 Hz. Una
versione (A) dell’amplificatore viene realizzata correttamente; un’altra (B), collegando per errore un
resistore da 10  fra l’ingresso invertente e massa.
Sapreste distinguerli? Eseguendo quali misure?
7) Calcolare il tempo di salita di un circuito RC passabasso che presenta attenuazione di 1 dB alla
frequenza di 50 kHz.
G. V. Pallottino – Agosto 2011
Università di Roma Sapienza - Dipartimento di Fisica
Appunti di Elettronica – Raccolta di esercizi
pag. 17