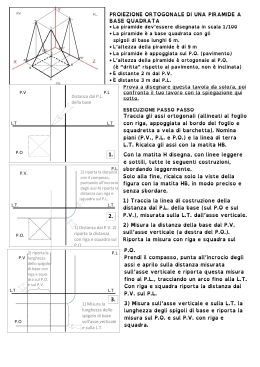
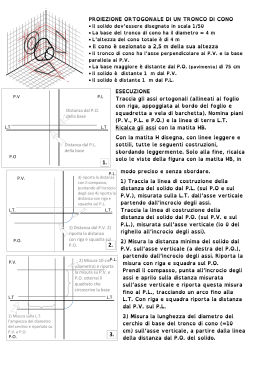
Prof. Alessandra Battistelli – P.O. di un tronco di piramide a base esagonale






P.V
.
P.L
.

Distanza dal P.O.
della base
L.T
.
L.T
.
Distanza dal P.L.
della base
P.O
.
P.V.
P.L.
3) riporta la distanza sulla
L.T. con il compasso,
puntando all’incrocio degli
assi
4) riporta la distanza con
riga e squadra sul P.L.
L.T.
L.T
.
1) Distanza dal P.V.
dell’asse
2) riporta la distanza
con riga e squadra sul
P.O.
2.
P.O.
1) Misura sulla L.T.
l’ampiezza massima
dell’esagono di base,
che è = a 2 lati ed è = al
diametro del cerchio
circoscritto
A
P.O.
B
A
0
B
L.T
.
2) Apri il compasso
della misura di un
lato = raggio del cerchio
circoscritto
3) Sul PO punta in A e
poi in B e traccia
3.
2 archi
P.O. tronco di piramide a base esagonale
P.L.
P.V.
L.T
.
1.
1
Prof. Alessandra Battistelli – P.O. di un tronco di piramide a base esagonale
P.V.
P.L.
1) Punta in 0 e traccia il
cerchio che circoscrive
l’esagono
2) Traccia i lati
dell’esagono, collegando
A, C, B, F, E
L.T
.
E
F
0
A
C
P.O.
P.V.
L.T
.
B
D
3) Riporta il centro 0,
dove cade l’asse del solido,
sul PV, con riga e squadra
4) Riporta gli angoli E-F e CD sull’asse verticale
4.
V
P.L.
V
1) Misura sull’asse
verticale l’altezza
totale del solido e
della sezione
L.T
.
E
F
C
P.O.
2) Riporta le
misure sul PV e sul
PL trovando V
3) Con riga e squadra
riporta gli angoli B,
C-E e D-F sul PV
B
0
0
A
L.T
.
D
5.
V
P.V.
V
P.L.
1) Sul PV collega
L.T
.
A
C
B
F
0
A
P.O.
D
C
E
B
D
E
A
C
L.T
.
2) Riporta gli angoli
di base sul PL con il
compasso e con riga
e squadra
3) Collegali poi a V 6.
P.V.
1) Riporta con
V
V
riga e squadra,
I LM
dal PV e dal PL G
sul PO, gli
angoli dell’
esagono della
sezione
L.T
A
.
2) Collega gli
angoli dell’
esagono A
della sezione
riportati sul
PO
P.O.
C
E
N P
Q
D B
F
B
C
D
P.L.
L.T
.
3) Collega gli angoli
della sezione con
gli angoli della base
4) Ricalca tutti gli
spigoli
7.
P.O. tronco di piramide a base esagonale
gli angoli della
base con V
2