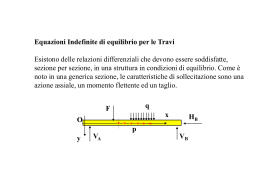
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Prima Facoltà di Architettura “Ludovico Quaroni”
Corso di Laurea 5 U.E.
A.A. 2001/2002 - II semestre
Note sulle lezioni del corso di
STATICA
tenute dal Prof. Luis Decanini
Con la collaborazione del Dott. Laura Liberatore
Parte 3
y
p
A
B
x
L
Diagramma
+
del Momento
pendenza
negativa
2
Mmax = 1/8 pL
pendenza
positiva
CARATTERISTICHE DELLA SOLLECITAZIONE
1
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
INDICE
1.1.
Schema strutturale .................................................................................................................3
1.1.1. Strutture – elementi strutturali .....................................................................................3
1.1.2. Classificazione degli elementi strutturali ..................................................................4
Travi .................................................................................................................................................4
Lastre e piastre .................................................................................................................................4
Solidi tridimensionali .......................................................................................................................5
1.1.3. Approfondimenti sugli elementi strutturali tipo travi .............................................6
1.1.4. Esempi di modellazione delle azioni esterne ...........................................................9
Carichi Gravitazionali......................................................................................................................9
Solaio ordito in una sola direzione.................................................................................................10
1.1.5. Le strutture nel piano ...................................................................................................11
Sistemi isostatici .............................................................................................................................12
Sistemi iperstatici ...........................................................................................................................13
1.2.
Caratteristiche della sollecitazione.....................................................................................14
1.2.1. Le azioni interne.............................................................................................................14
1.2.2. La sollecitazione nella sezione ..................................................................................17
1.2.3. Corpo spaziale tipo trave.............................................................................................21
1.3.
Casi particolari di sollecitazione .........................................................................................28
1.3.1. Sistema piano .................................................................................................................28
1.3.2. Sollecitazione di flessione e taglio............................................................................31
1.3.3. Sollecitazione di sforzo normale e flessione..........................................................32
1.3.4. Sollecitazione di compressione o di trazione ........................................................34
1.4.
Diagrammi delle caratteristiche della sollecitazione........................................................35
1.4.1. Caratteristiche della sollecitazione nei sistemi piani...........................................38
Impostazione del problema - Definizione delle caratteristiche della sollecitazione ......................38
Convenzioni sui segni delle caratteristiche della sollecitazione ....................................................43
1.4.2. Relazioni differenziali tra i carichi ripartiti e le caratteristiche della
sollecitazione..................................................................................................................................47
Osservazioni ...................................................................................................................................51
Applicazione: Trave appoggiata con carico concentrato...............................................................52
Applicazione: Trave appoggiata con carico ripartito uniforme.....................................................57
Applicazione: Trave appoggiata con carico ripartito lineare ........................................................64
Applicazione: Trave incastrata con carico uniformemente ripartito .............................................69
Applicazione: Trave rettilinea soggetta a diversi tipi di carico .....................................................71
1.4.3. Caratteristiche della sollecitazione per travi costituite da tratti inclinati e
orizzontali ........................................................................................................................................80
Applicazione: Trave a ginocchio per rampa di scala.....................................................................83
Applicazione: Trave a ginocchio con carico ripartito uniforme ....................................................93
Applicazione: Sistema di travi articolate .....................................................................................105
1.5.
Applicabilità dell’ipotesi di corpo rigido nella determinazione delle caratteristiche della
sollecitazione ......................................................................................................................................114
2
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.1. Schema strutturale
1.1.1. Strutture – elementi strutturali
In senso lato una struttura resistente può essere definita come un insieme di elementi
collegati fra loro capaci di trasmettere azioni esterne a corpi circostanti.
La trasmissione delle azioni esterne (forze, deformazioni imposte, ecc.) usualmente si
verifica in modo tale che la struttura resiste conservando sostanzialmente la propria posizione rispetto ai corpi circostanti (terra, altre strutture).
Tuttavia la conservazione della posizione non esclude variazioni più o meno significative della forma a causa delle deformazioni.
Come già segnalato, i materiali strutturali (cemento armato, acciaio, legno, murature,
ecc.) sono tutti più o meno deformabili (non rigidi) e perciò gli elementi strutturali da
essi costituiti tendono a cambiare di forma sotto l’effetto delle azioni esterne.
Nonostante tutte le strutture risultino in minor o maggior misura deformabili, il modello
di corpo rigido risulta accettabile in numerosi casi e, comunque, è necessario per la
comprensione del comportamento strutturale.
Nell’ambito dell’architettura si può affermare che le strutture resistenti hanno il compito
di opporsi alle azioni esterne senza movimento (stato di quiete - equilibrio) anche se deformate.
3
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.1.2. Classificazione degli elementi strutturali
Dal punto di vista della Scienza delle Costruzioni, gli elementi strutturali che possono
costituire una struttura, in funzione della loro geometria e degli sforzi interni prevalenti si classificano in: Travi; Lastre e Piastre; Solidi Tridimensionali.
Travi
Presentano una dimensione predominante rispetto alle altre due, pertanto possono
essere caratterizzate come solidi monodimensionali.
asse
Lastre e piastre
Sono caratterizzate dall’avere due dimensioni predominanti rispetto alla terza (spessore), pertanto possono essere trattati come solidi bidimensionali.
La distinzione fra lastre e piastre deriva dalla direzione prevalente degli sforzi interni rispetto alla loro superficie media.
•
Nelle lastre gli sforzi interni sono prevalentemente paralleli alla superficie media (problema piano di tensioni); risulta quindi preponderante il comportamento
assiale.
•
Nelle piastre gli sforzi interni sono prevalentemente ortogonali alla superficie
media; predomina il comportamento flessionale.
4
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
LASTRE
s
s
s: spessore
s
PIASTRE
s
s
s: spessore
Solidi tridimensionali
Le tre dimensioni sono dello stesso ordine di grandezza.
plinto di fondazione
fondazione macchinario
5
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.1.3. Approfondimenti sugli elementi strutturali tipo travi
Nel presente Corso, l’attenzione sarà prevalentemente rivolta a strutture costituite da elementi strutturali tipo trave.
Da un punto di vista geometrico, una trave è un solido generato da una qualunque area
piana che si sposta nello spazio in maniera tale che il suo baricentro percorra una data
linea e che l’area si mantenga sempre ortogonale a questa linea. In altre parole, una trave è un corpo allungato generato da una figura piana che si sposta nello spazio conservandosi ortogonale alla linea descritta dal suo baricentro.
sezione
retta
linea
d’asse
Il luogo geometrico dei baricentri delle sezioni rette costituisce l’asse geometrico della
trave.
Nessuna limitazione viene imposta alla forma della linea dell’asse, che può essere una
qualsiasi linea nello spazio. Di solito si tratta di una linea piana e frequentemente è una
linea retta (travi ad asse rettilineo).
trave ad asse rettilineo
trave a linea d’asse sghemba
trave piana curva
(la linea d’asse è una curva
contenuta un un piano)
6
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
L’area ha dimensioni piccole rispetto alla lunghezza dell’asse (solido allungato); la sezione può cambiare di forma e dimensioni lungo la linea d’asse purché gradualmente e
con continuità.
Benché la sezione retta possa cambiare, spesso si mantiene invariata (trave di sezione
costante).
Due esempi di strutture costituite da travi
In senso lato, gli archi possono essere considerati solidi monodimensionali di tipo trave
(asse piano curvilineo)
arco a tutto sesto
arco a sesto acuto
Benché nessuna limitazione venga imposta alla forma della sezione retta delle travi, tale
forma risulta spesso associata al tipo di materiale impiegato.
legno
c. armato
muratura
c. armato
7
c. armato
acciaio
precompresso
acciaio
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
I concetti di sollecitazione e delle corrispondenti azioni interne possono essere agevolmente introdotti nelle tipologie strutturali derivanti dall’impiego della trave. Infatti,
come si vedrà più avanti, la valutazione del Risultante e del Momento Risultante di tutte
le forze esterne che precedono (o seguono) una data sezione retta può essere generalmente effettuata considerando l’ipotesi di corpo rigido e applicando le condizioni di equilibrio.
Nell’ambito delle costruzioni dell’Architettura è possibile riconoscere una tipologia
molto ricca di varietà espressive costituita da solidi monodimensionali (travi) diversamente assemblati. Tuttavia gli elementi strutturali (travi) sono organizzati secondo
un’adeguata gerarchia statica (sistema principale, elementi secondari, ecc.)
Percorso dei carichi:
SOLAIO
Ø
TRAVE SECONDARIA
Ø
TRAVE PRINCIPALE
Ø
PILASTRO
8
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.1.4. Esempi di modellazione delle azioni esterne
Carichi Gravitazionali
qs e p includono
carichi permanenti e sovraccarichi
Percorso dei carichi:
PIASTRA Ö TRAVE Ö PILASTRO Ö FONDAZIONE Ö TERRENO
qs:
[kN/m2] carico uniforme agente sull’unità di superficie del solaio;
p:
[kN/m] carico uniforme agente sull’unità di lunghezza della trave;
P:
[kN]
carico concentrato agente sul pilastro.
9
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
p = qs
B
;
2
P=p
L
B⋅L
= qs
2
4
σt = Reazione del terreno di fondazione (forza sull’unità di superficie [kN/m2]).
Solaio ordito in una sola direzione
Modellazione dei carichi e schema statico
p = qs x interasse
P = t x interasse
10
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.1.5. Le strutture nel piano
La maggior parte delle costruzioni costituiscono una realtà spaziale tridimensionale in
quanto circoscrivono volumi e spazi, perciò il concetto di struttura o sistema piano merita ulteriori chiarimenti.
Nella costruzione spaziale si possono individuare modelli statici piani, cui spettano funzioni portanti sufficientemente precise, che semplificano il modello senza sacrificare la
sicurezza della struttura. Il complesso strutturale può essere allora immaginato come
composto da una serie di sistemi piani.
Su questi piani, che contengono i corrispondenti assi geometrici, possono essere portati
ad agire i carichi ripartiti e concentrati che loro competono.
Un tipico esempio di struttura tridimensionale sono le ossature in cemento armato o in
acciaio degli edifici. In prima approssimazione, esse possono essere analizzate considerando sistemi piani orientati secondo le due direzioni principali della costruzione.
Così la struttura spaziale viene decomposta in una serie di sistemi piani la cui risoluzione risulta più agevole. Tuttavia è necessario tenere conto di eventuali effetti dovuti alla
continuità tra i diversi sistemi piani.
I seguenti schemi strutturali illustrano diversi casi di sistemi piani costituiti da travi.
11
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Sistemi isostatici
12
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Sistemi iperstatici
13
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.2. Caratteristiche della sollecitazione
1.2.1. Le azioni interne
Dopo aver determinato le reazioni vincolari è necessario studiare le azioni interne, cioè
le “sollecitazioni”, cui si trovano soggette le sezioni di un corpo rigido vincolato. In altre parole, note tutte le forze attive e reattive che agiscono sul corpo si cercano le interazioni scambiate attraverso una generica sezione piana “s” del corpo (analisi statica interna).
Le azioni interne forniscono delle informazioni sullo stato di sforzo in cui si trova un
corpo soggetto ad un sistema di forze attive e reattive equilibrato.
Si prenda in esame il corpo rigido vincolato spaziale (tridimensionale) soggetto ad un
insieme di forze concentrate e vincolato esternamente in A e B in modo adeguato
(Figura 1.a). Possiamo considerare una sezione piana “s” (ortogonale all’asse del corpo)
che divide il corpo originale in due parti: una che precede la sezione e che denominiamo
corpo 1, ed un’altra che segue la sezione e che chiamiamo corpo 2 (Figura 1.b). I due
corpi 1 e 2 sono connessi attraverso un “vincolo di continuità” lungo la sezione piana
“s”.
Immaginiamo di operare un distacco dei due corpi: il mantenimento delle condizioni di
equilibrio è verificato grazie alla presenza delle azioni interne scambiate dai due corpi
attraverso la sezione “s”. Queste azioni possono essere viste anche come forze elementari (o forze molecolari) interne scambiate tra gli elementi della superficie delle due facce a contatto con la sezione. Così ∆ R1 saranno le forze interne elementari che il corpo 1
trasmette al corpo 2 e ∆ R 2 le forze interne elementari che il corpo 2 trasmette al corpo
1. Per l’equilibrio dovrà risultare ∆ R 2 = − ∆ R 1 (Figura 1.c). In una prima analisi le for-
ze elementari possono essere ricondotte ad un sistema equivalente costituito da una forza risultante ed un vettore momento risultante che agiscono su ciascuna delle facce della
sezione. Si prenderanno quindi in esame il risultante R1 e il vettore momento risultante
M 1 , che equivalgono complessivamente a tutte le forze elementari ∆ R1 , ed il risultante
R 2 e il vettore momento risultante M 2 , che equivalgono complessivamente a tutte le
forze elementari ∆ R 2 (Figura 1.d).
Il risultante R1 e il momento risultante M 1 sono la riduzione al baricentro G della sezione di tutte le forze attive e reattive che agiscono sul corpo 1. Infatti, se l’intero corpo
14
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
è in equilibrio il sistema costituito da tutte le forze attive e reattive applicate al corpo 1
(sistema A) più il sistema costituito da tutte le forze attive e reattive agenti sul corpo 2
(sistema B) dovrà essere nullo, inoltre per l’equilibrio del corpo 2 il sistema costituito
da R1 e M 1 (sistema S) più quello delle forze attive e reattive agenti sul corpo 2 (B)
dovrà essere nullo, se ne deduce immediatamente che il sistema di forze attive e reattive
applicate al corpo 1 e il sistema costituito da R1 ed M 1 sono equivalenti:
equilibrio dell’intero corpo: A + B = 0
equilibrio del corpo 2:
S+B=0
⇒ A=S
In maniera analoga il risultante R 2 e il momento risultante M 2 sono la riduzione al baricentro G della sezione di tutte le forze attive e reattive che agiscono sul corpo 2.
Per la determinazione di R1 , M 1 , R 2 ed M 2 è sufficiente l’applicazione delle equazioni di equilibrio (equazioni cardinali della statica) mentre la determinazione delle forze
interne elementari (e quindi delle tensioni) richiede ulteriori ipotesi. In altre parole il
calcolo di R1 , M 1 , R 2 ed M 2 , che rappresentano in maniera generalizzata lo stato di
sforzo nella sezione “s”, si può risolvere con l’ipotesi di corpo rigido e mediante
l’applicazione delle equazioni di equilibrio. Per la determinazione dettagliata delle forze
interne elementari (tensioni) ∆ R1 e ∆ R 2 che si sviluppano nella sezione “s” oltre alle
equazioni della statica è necessaria la conoscenza delle deformazioni che soffre il materiale e quindi l’ipotesi di corpo rigido non è sufficiente. Ad ogni modo le forze interne
elementari (o i loro equivalenti complessivi) trasmesse da una parte all’altra del corpo
attraverso la sezione “s” equilibrano tutte le forze (attive e reattive) agenti sulla parte a
cui sono trasmesse.
Nel seguito si tratta il problema della determinazione della sollecitazione nella sezione e
si esaminano le componenti di tale sollecitazione, denominate caratteristiche della sollecitazione.
15
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
f1
f3
f2
f4
f5
a) Corpo rigido vincolato
A
f11
B
f12
f13
f21
RA
RB
s
f12
b) Sistema di forze attive e reattive,
la sezione piana “s” divide il
corpo in due parti.
2
1
f12
f22
f13
∆R1
f21
∆R2
f22
c) Forze molecolari
interne.
2
1
RA
RB
∆R1 = - ∆R2
f12
f12
f13
f21
R1
M2
G
1
RA
M1
G
R2
Figura 1
16
f22
d) Sollecitazione
nella sezione “s”.
2
RB
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.2.2. La sollecitazione nella sezione
Si consideri una generica sezione normale “s” del corpo esaminato (assimilabile ad una
trave). La riduzione al polo G (baricentro della sezione) del sistema delle forze attive e
reattive che agiscono sulla parte che precede la sezione “s” (corpo 1 in Figura 1.d), si
può realizzare trasportando ogni forza nel punto G e aggiungendo la corrispondente
coppia di trasporto. In tale modo il sistema di forze considerato si riduce ad un insieme
di forze concorrenti in G e ad un insieme di coppie di trasporto. Le forze concorrenti
possono essere sommate dando luogo al risultante R1 applicato in G. Anche le coppie
possono essere sommate, esse danno luogo ad una coppia risultante M 1 (Figura 2).
Come detto, R1 ed M 1 rappresentano l’azione che il corpo 1 trasmette al corpo 2 attraverso la sezione “s” (Figura 3).
Operando in modo analogo sulla parte che segue la sezione “s” (corpo 2) si ottengono il
risultante R 2 applicato in G ed il momento risultante M 2 . R 2 ed M 2 rappresentano
l’azione che il corpo 2 trasmette al corpo 1 attraverso la sezione “s” (Figura 3).
Se il sistema complessivo di forze è in equilibrio, i due sistemi risultanti devono costituire un sistema equivalente a zero (Figura 2).
SOLLECITAZIONE nella sezione “s”
f12
f12
f13
f21
R1
M2
G
1
M1
R2
RA
G
f22
2
RB
G = baricentro sezione “s”
R1 ed M1 costituiscono la SOLLECITAZIONE nella sezione
Figura 2
17
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
{ f1 } + R A
= insieme delle forze attive e reattive che agiscono sul corpo 1
Riduzione al polo G dell’insieme delle forze che agiscono sul corpo 1
R1 = ∑ f 1i + R A
i
M 1 = ∑ (Pi − G ) ∧ f 1i + ( A − G ) ∧ R A
i
{F1 } = sollecitazione nella sezione “s”


{F1 } =  R1 
M 1 
{ f 2 }+ R B
= forza generalizzata (polo G / corpo 1)
= insieme delle forze attive e reattive che agiscono sul corpo 2
Riduzione al polo G dell’insieme delle forze che agiscono sul corpo 2
R2 = ∑ f 2i + R B
i
M 2 = ∑ (Pi − G ) ∧ f 2i + (B − G ) ∧ R B
i


{F2 } =  R 2 
= forza generalizzata (polo G / corpo 2)
{F1 } = −{F2 }
il sistema complessivo è in equilibrio
M 2 
EQUILIBRIO CORPO 2
f21
Per definizione R1 ed M1 costituiscono la
M1
SOLLECITAZIONE nella sezione “s”
G
2
R1
a) il sistema {F1 } può essere visto come l’azione che il corpo 1
trasmette al corpo 2 per effetto della CONTINUITA’
b) il corpo 2 rimane in equilibrio sotto le azioni delle forze ad
esso applicate e delle azioni {F1 } trasmessegli dal corpo 1 in
G
18
f22
RB
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
EQUILIBRIO CORPO 1
f12
f12
f13
R2
G
M2
1
RA
Figura 3
a) il sistema {F2 } può essere visto come l’azione che il corpo
2 trasmette al corpo 1 per effetto della CONTINUITA’
b) il corpo 1 rimane in equilibrio sotto le azioni delle forze ad
esso applicate e delle azioni {F2 } trasmessegli dal corpo 2
in G
R1 , R 2 e M 1 , M 2 saranno eguali in modulo, opposti in verso e coincidenti in retta
d’azione, come è necessario per l’equilibrio, ne segue che:
R1 = − R 2
M 1 = −M 2
Si chiama sollecitazione nella sezione “s” il sistema formato da R1 ed M 1 (oppure il
sistema R 2 , M 2 con segni cambiati). In maniera generica (indipendentemente dagli indici) la sollecitazione nella sezione “s” è definita dalla forza risultante R S e dal momento risultante M S , rispetto al polo G, delle forze attive e delle reazioni vincolari che precedono la sezione “s”.
Si osserva che R S e M S rappresentano l’azione che la parte di corpo che precede la sezione “s” trasmette alla parte di corpo che segue la sezione “s”.
Sollecitazione nella sezione “s”:
•
Forza Risultante Rs
•
Momento Risultante M s
Ms
Rs
19
G
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
R S e M S mettono in evidenza lo stato di sforzo nella sezione “s” derivato dalle forze
applicate (attive e reattive). I risultanti R S e M S possono essere visti come una forza
 RS 
generalizzata F S = 
 , il vettore F S è quindi la sollecitazione nella sezione “s”.
M S 
{ }
{ }
La forza risultante R S ed il momento risultante M S costituiscono i parametri generalizzati della sollecitazione.
Spostando la sezione “s” lungo l’asse del corpo, la sollecitazione varia. Questo come
conseguenza dello spostamento del polo di riduzione G (spostamento del baricentro
lungo l’asse del corpo) e della presenza di nuove forze nella parte del corpo che precede
la sezione considerata.
f1
f3
f2
f4
RA
sezione s
MS
RS
G
f5
G
G*
s
s*
asse del corpo
RB
sezione s*
La sollecitazione varia con la
M*S
localizzazione della sezione
G*
rispetto all’asse del corpo
R*S
 R *S 
 RS 
*
{FS } =   ≠ {FS }=  * 
 M S 
M S 
20
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.2.3. Corpo spaziale tipo trave
Le componenti del vettore forza generalizzata {FS } sono denominate caratteristiche
della sollecitazione. Le sei componenti (tre di R S e tre di M S ) secondo gli assi di rife-
rimento sono quindi le caratteristiche della sollecitazione nella sezione “s”.
Le caratteristiche della sollecitazione si definiscono mediante un particolare sistema di
assi con origine nel baricentro G della sezione (Figura 4). L’asse “x” è normale al piano
della sezione e coincidente con l’asse del corpo se rettilineo o con la tangente ad esso in
G se l’asse del corpo è curvilineo. Gli assi “y” e “z” si trovano nel piano della sezione e
sono coincidenti con gli assi principali d’inerzia della sezione normale “s”. I versi indicati nella Figura 4 sono quelli assunti convenzionalmente quali positivi per le caratteristiche della sollecitazione.
Nel caso più generale, la sollecitazione nella sezione “s” ha sei componenti (tre di forza
e tre di momento) come è illustrato nella Figura 5:
a) Le tre componenti, secondo gli assi, del Risultante delle forze R S sono:
 RSx 
{RS } =  RSy 
R 
 Sz 
R Sx = ∑ f1xi + R Ax
i
R Sy = ∑ f1yi + R Ay
i
R Sz = ∑ f1zi + R Az
i
RSx, RSy, RSz, costituiscono tre forze applicate nel baricentro G ed agenti secondo gli
assi x, y e z.
b) Le tre componenti, secondo gli assi, del vettore Momento Risultante M S
M S = ∑ (Pi − G ) ∧ f 1i + ( A − G ) ∧ R A
i
 M Sx 
{M S } =  M Sy 
M 
 Sz 
le componenti MSx, MSy e MSz possono essere viste come tre coppie giacenti in piani
normali agli assi x, y e z.
21
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
TERNA LOCALE DI RIFERIMENTO
y
z
linea d’asse
G
x
parte del corpo che segue
la sezione esaminata
Si considera un corpo assimilabile ad una trave. Per la definizione delle caratteristiche
della sollecitazione in una data sezione si fa riferimento ad una particolare terna di assi
ortogonali con origine nel baricentro G.
• Asse x: orientato secondo la direzione perpendicolare alla sezione, con verso uscente
da essa. L’asse x coincide con l’asse del corpo se rettilineo o con la tangente
ad esso in G se curvilineo.
• Asse y: orientato secondo la direzione della retta intersezione tra il piano medio del
corpo (trave) ed il piano contenente la sezione, con verso diretto verso l’alto.
• Asse z: orientato secondo la normale al piano medio con verso positivo entrante.
Quindi l’asse z risulta essere la binormale alla linea d’asse.
Gli assi y e z risultano paralleli agli assi principali di inerzia della sezione.
Figura 4
22
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
y
Per ogni sezione “s” le
z
caratteristiche della sollecitazione
sono le componenti del sistema
x
costituito da RS ed MS
MS
RS
Componenti del Risultante Rs
y
- Rsx = N sforzo assiale (o sforzo normale)
z
- Rsy = Ty sforzo di taglio
- Rsz = Tz sforzo di taglio
Rs x
x
Rsz
Rsy
N : direzione ortogonale alla sezione
Ty e Tz : direzioni parallele al piano della sezione
Rs
Componenti del Momento Risultante Ms
y
- Msy, Msz = momenti flettenti
- Msx = Mt = momento torcente
z
Msy, Msz : vettori momento ortogonali
Msx
x
Ms
all’asse della trave
Msz
Mt : vettore momento parallelo all’asse
Msy
della trave
Figura 5
23
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Alle caratteristiche della sollecitazione si danno nomi legati agli effetti che producono
sul corpo. Le sei componenti nel caso più generale (spaziale) sono:
¾ Forze
Rsx = N
Sforzo Normale (o Sforzo Assiale)
Rsy = Ty
Sforzo di Taglio secondo y
Rsz = Tz
Sforzo di Taglio secondo z
¾ Momenti
Msx = Mt
Momento Torcente
Msy = Msy
Momento Flettente (vettore momento parallelo ad y)
Msz = Msz
Momento Flettente (vettore momento parallelo a z)
• L’effetto della forza normale N in prossimità della sezione “s” è quello di tendere o
comprimere (allungare o accorciare) il corpo (N è perpendicolare alla sezione).
• Gli sforzi di taglio Ty e Tz agiscono nel piano della sezione e tendono a “tagliare” il
corpo secondo la sezione “s”.
• La componente Mt si chiama momento torcente perché tende a “torcere” il corpo. Il
vettore Msx = Mt è parallelo all’asse “x” (asse del corpo), ovvero la coppia corrispondente è giacente nel piano “yz”. In altre parole la coppia del momento torcente è contenuta nel piano della sezione (Figura 6).
• La componente Msz è denominata momento flettente perché inflette il corpo. Alcuni
autori chiamano questa componente “momento flettente verticale” oppure “momento
flettente principale”. Il vettore Msz è parallelo all’asse “z” e la coppia corrispondente
giace nel piano “xy”, che spesso è un piano verticale (Figura 7). Come si vedrà più
avanti questo momento è l’unico esistente nel caso particolare delle travi ad asse rettilineo per stati di sollecitazione piani e si chiama direttamente “momento flettente”.
• Anche la componente Msy è denominata momento flettente poiché anch’essa tende
ad inflettere il corpo. Taluni chiamano questa componente “momento flettente orizzontale” oppure “momento flettente secondario”. Il vettore Msy è parallelo all’asse
“y” e la coppia corrispondente giace nel piano “xz”, che spesso è un piano orizzontale (Figura 8).
24
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
y
Per chiarezza vengono rappresentati
sia il vettore momento che la
z
corrispondente coppia
x
Mt
Ms x = Mt
Mt
Piano “yz” (piano della sezione)
Effetto del Momento Torcente Mt
Trave
Mt
Mt
Deformazione
Il vettore momento è parallelo all’asse “x” (asse della trave), ovvero la coppia corrispondente è giacente nel piano “yz” (la coppia è contenuta nel piano della sezione).
Figura 6
25
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
y
z
Piano “xy” (piano verticale,
Msz
x
perpendicolare all’asse “z”)
Msz
Il vettore momento è parallelo all’asse “z” e la coppia corrispondente giace nel piano
“xy”.
Il momento Msz si chiama momento flettente perché inflette la trave secondo il piano
verticale.
Effetto del momento flettente Msz
Trave
Deformazione
(incurvamento verticale)
Figura 7
26
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
y
z
Msy
Piano “xz” (piano orizzontale,
tangente alla linea d’asse)
x
Msy
Il vettore momento è parallelo all’asse “y” e la coppia corrispondente giace nel piano
“xz”.
Il momento Msy si chiama momento flettente perché inflette la trave secondo il piano orizzontale.
Effetto del momento flettente Msy
Trave
Deformazione in pianta
(incurvamento orizzontale)
Figura 8
27
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.3. Casi particolari di sollecitazione
1.3.1. Sistema piano
Se il piano π, che contiene l’asse della trave e tutte le forze attive e reattive, contiene inoltre uno degli assi principali di inerzia della sezione si annullano: il momento torcente, uno degli sforzi di taglio, uno dei momenti flettenti (Figura 9 e Figura 10, nella costruzione grafica il piano π coincide con il piano di rappresentazione). Di conseguenza
nel caso piano le caratteristiche della sollecitazione sono tre: lo sforzo normale, uno
sforzo di taglio ed un momento flettente. Poiché esiste soltanto un momento flettente si
ha flessione retta:
Caratteristiche della sollecitazione in un
Æ
sistema piano
 N 
 N 




 T y  oppure  Tz 
M 
M 
 Sz 
 Sy 
Nel caso della Figura 9 il piano π contiene l’asse principale d’inerzia “y”; il risultante
R S è anch’esso contenuto in tale piano quindi la sua componente secondo “z” è nulla.
Inoltre il vettore momento risultante M S è normale al piano π e quindi non ha componenti secondo gli assi “x” e “y”. Si noti che la coppia corrispondente a M S è contenuta
nel piano π.
Quindi si ha:
Æ
Caratteristiche della sollecitazione
28
 N   N 

 

 T y  =  TS 
M  M 
 Sz   S 
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
y
f21
piano π (piano “xy”)
f22
z
x
Msz
Rs
π
RB
Se il piano contiene tutte le forze (attive e reattive esterne) e l’asse della trave, nonché
uno degli assi principali d’inerzia della sezione allora la trave costituisce un sistema piano e si annullano: il momento torcente Mt, uno dei due sforzi di taglio e uno dei due
momenti flettenti.
y
y
z
z
N
G
x
Rs
G
x
Ty
Msz
y
N
Ty
z
Rs
piano π =
piano “xy”
π
Msz
x
il risultante RS è contenuto
vettore Msz
nel piano “xy”
il vettore MS è normale al piano
“xy” e la coppia corrispondente
giace nel piano “xy”
Figura 9
29
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
s
M, N e T = caratteristiche della
sollecitazione = Riduzione a G
di tutte le forze che precedono la
N
G
M
T
sezione s
s
Figura 10
30
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.3.2. Sollecitazione di flessione e taglio
Spesso si presenta il caso di travi rettilinee soggette a forze attive e reattive perpendicolari all’asse della trave. Se tutte queste forze sono contenute in un piano che contiene
inoltre uno degli assi principali d’inerzia della sezione, esistono soltanto le caratteristiche della sollecitazione M e T, cioè flessione e taglio (Figura 11 e Figura 12). Essendo
le forze agenti normali all’asse della trave, la componente secondo tale asse è nulla (N =
0). Frequentemente l’asse della trave è orizzontale e le forze (pesi) agiscono nella direzione verticale.
Sollecitazione di FLESSIONE E TAGLIO (sforzo normale nullo)
P
P = carico concentrato
1/3 L
P
1/3 L
2/3 L
s
2/3 L
G
x
1/3P
2/3P
R=1/ 3P
R=2/ 3P
+ 2/3P
T
+
Sezione s (x ≥ 1/3L)
- 1/ 3P
-
N = ∑ Fxi = 0
i
T = ∑ Fyi =
i
M = ∑ M Gi
i
2
P
P−P=−
3
3
P
L
=− x+P
3
3
M
+ 2/9P
+
Figura 11
31
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Sollecitazione di FLESSIONE E TAGLIO (sforzo normale nullo)
p = carico ripartito
le forze sono perpendicolari
all’asse della trave
il piano π contiene uno degli
S
assi principali di inerzia della
piano π
sezione
esistono soltanto
flessione M = M
y
e taglio T = RS
z
G
x
asse della trave
M
Ms
T
Rs
S
Figura 12
1.3.3. Sollecitazione di sforzo normale e flessione
Se il risultante di forze e reazioni vincolari che precedono (o seguono) la sezione incontra il piano della sezione in un punto di uno degli assi principali d’inerzia ed inoltre tale
risultante è parallelo all’asse della trave rettilinea, si avrà sollecitazione di flessione retta
e di sforzo normale (Figura 13.a).
Se tutte le forze attive e reattive che precedono la sezione si riducono ad una forza risultante parallela all’asse della trave rettilinea e che incontra il piano della sezione in un
punto non appartenente ad uno degli assi principali, si avrà sollecitazione di sforzo
normale e flessione biassiale (deviata) come illustrato in Figura 13.b.
In questi casi essendo il risultante RS parallelo all’asse della trave non esistono componenti trasversali all’asse, cioè non ci sono né sforzi di taglio né momento torcente.
32
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
In seguito si considera il caso in cui il risultante parallelo all’asse incontra il piano della
sezione in un punto appartenente ad uno degli assi principali d’inerzia (sforzo normale e
flessione retta). In queste condizioni si dice che la sollecitazione è di flessione retta
composta: la così detta presso-flessione se lo sforzo normale è di compressione, o tenso-flessione se lo sforzo normale è di trazione.
La sollecitazione di presso-flessione si presenta nei pilastri quando all’estremità agisce
un carico eccentrico o anche quando l’estremità è collegata ad un altro elemento strutturale che le trasmette una forza assiale ed un momento (Figura 14).
Sollecitazione di SFORZO NORMALE E FLESSIONE
G
G
P
P
a) flessione retta
e sforzo normale
b) flessione biassiale
e sforzo normale
Figura 13
Esempi di PRESSO-FLESSIONE
P
e
p
p
M=P xe
=
=
P
e = eccentricità
P = carico concentrato
Figura 14
33
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.3.4. Sollecitazione di compressione o di trazione
Quando il risultante di tutte le forze (attive e reattive) che agiscono sulla parte di trave
che precede (o segue) la sezione considerata, coincide con l’asse della trave (se questa è
rettilinea) o con la tangente all’asse nel baricentro della sezione (nel caso di asse curvilineo), la sollecitazione nella sezione si riduce al solo sforzo normale N (Figura 15). Lo
sforzo assiale può essere di compressione o di trazione.
Spesso si presenta il caso di trave soggetta a solo sforzo normale in tutte le sezioni (pilastri con carico centrato, aste dei sistemi reticolari, tiranti, archi funicolari, catenarie,
ecc.)
Sollecitazione di TRAZIONE o COMPRESSIONE
il risultante
coincide con
l’asse della trave
il risultante
coincide con
l’asse della trave
sollecitazione di
compressione
sollecitazione di
trazione
Figura 15
34
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.4. Diagrammi delle caratteristiche della sollecitazione
Come si è visto in precedenza, la sollecitazione ( R S , M S ) varia quando si sposta la sezione “s” lungo l’asse della trave. Questo come conseguenza dello spostamento del baricentro lungo l’asse predetto (variazione della posizione del polo di riduzione) e della
presenza di nuove forze nella parte del corpo che precede la sezione considerata. Ad
ogni punto della linea d’asse corrisponde una sezione trasversale (cioè ortogonale alla
linea d’asse) e conseguentemente una sollecitazione.
Naturalmente se cambiano i valori della sollecitazione, variano anche i valori delle sue
componenti. Quindi i valori delle caratteristiche della sollecitazione dipendono dalla posizione della sezione che si considera. I diagrammi delle caratteristiche della sollecitazione sono la rappresentazione grafica dell’andamento di queste caratteristiche al variare della posizione della sezione lungo l’asse della trave. Questi diagrammi indicano
gli effetti di un sistema di carichi fissi su tutte le sezioni della struttura. Nel caso più generale si avranno:
Diagrammi di:
Sforzo Normale
¾ N
Sforzi di Taglio
¾ Ty; Tz
Momenti Flettenti
¾ My; Mz
Momento Torcente ¾ Mt
In genere si usa l’asse della trave come linea di riferimento per il tracciato dei diagrammi. Se al percorso dell’asse della trave si associa una coordinata particolare “s”, le caratteristiche della sollecitazione risultano funzioni di tale coordinata. Queste funzioni sono
del tipo: CS = ϕ (s) dove CS è una generica caratteristica della sollecitazione ed “s” è
l’ascissa misurata lungo l’asse longitudinale della trave. Nel caso più generale si avrà:
•
N = ϕ 1 ( s)
Variazione dello Sforzo Normale
•
Ty = ϕ2 (s)
Variazione del Taglio secondo y
•
Tz = ϕ3 (s)
Variazione del Taglio secondo z
¾
Mt = ϕ4 (s)
Variazione del Momento Torcente
¾
My = ϕ 5 ( s )
Variazione del Momento Flettente secondo y
¾
Mz = ϕ6 (s)
Variazione del Momento Flettente secondo z
35
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Come si è detto, i diagrammi delle caratteristiche della sollecitazione costituiscono la
rappresentazione grafica delle suddette funzioni. O, in altre parole, i diagrammi suddetti
esprimono la variazione degli sforzi interni lungo l’asse della trave.
Calcolate le caratteristiche della sollecitazione in un numero conveniente di sezioni, si
disegna l’asse della trave e si tracciano le rette normali a detto asse nelle sezioni predette, su queste rette si riportano in scala i valori ottenuti della caratteristica considerata.
Unendo i punti rappresentativi dei valori della caratteristica della sollecitazione esaminata si ottiene il corrispondente diagramma.
I diagrammi delle caratteristiche della sollecitazione danno una visione generale degli
sforzi cui è soggetta una struttura per un certo sistema di forze agenti e sono di particolare interesse per le verifiche di stabilità e sicurezza. Forniscono poi un utile orientamento per stabilire una configurazione strutturale adatta a resistere agli sforzi cui sarà
soggetta la struttura. Inoltre il tracciamento dei diagrammi permette una verifica ulteriore delle condizioni di equilibrio e sono di utilità per il controllo dei risultati numerici
forniti dalle operazioni di calcolo delle caratteristiche della sollecitazione.
Nella Figura 16 è riportato, a titolo d’esempio, il diagramma dello sforzo normale relativo ad un pilastro soggetto ad un sistema di carichi assiali, mentre in Figura 17 sono riportati i diagrammi delle caratteristiche della sollecitazione per una trave ad asse curvilineo.
P
P
Diagramma
Sforzo Normale
(compressione)
P
2P
P
P
P
N=
2P
P
-
3P
P
4P
P
N=
4P
Figura 16
36
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Figura 17
37
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.4.1. Caratteristiche della sollecitazione nei sistemi piani
Nei paragrafi precedenti è stato esposto il problema generale riguardante la sollecitazione nei corpi tipo trave nello spazio. Successivamente sono stati studiati come casi particolari i sistemi piani. Tuttavia si ritiene opportuno esaminare ancora dettagliatamente le
strutture piane, date la loro importanza. Naturalmente, nel presente corso si farà riferimento ai sistemi isostatici, benché i concetti sulle caratteristiche della sollecitazione
siano applicabili anche ai sistemi iperstatici.
Giova ricordare che la valutazione delle azioni interne in una data sezione costituisce un
passaggio necessario per arrivare all’analisi degli stati tensionali.
Dato che le caratteristiche della sollecitazione possono variare da sezione a sezione,
l’analisi di tali variazioni si può effettuare mediante il tracciamento dei corrispondenti
diagrammi, che forniscono l’andamento degli sforzi interni lungo l’asse della trave e
danno utili informazioni per la verifica delle tensioni, e più in generale illustrano il funzionamento meccanico della struttura considerata. Peraltro i diagrammi possono guidare
la progettazione di forma e dimensioni della struttura.
Per il tracciamento dei diagrammi delle caratteristiche della sollecitazione sono di notevole importanza i legami analitici esistenti tra i carichi e la azioni interne (vedi relazioni
differenziali tra i carichi ripartiti e le caratteristiche della sollecitazione).
Nei sistemi piani le caratteristiche della sollecitazione sono tre (sforzo normale, sforzo
di taglio, momento flettente), ma tale numero può essere inferiore in casi particolari.
Impostazione del problema - Definizione delle caratteristiche della sollecitazione
Si consideri la trave rettilinea appoggiata agli estremi e soggetta ad un generico sistema
di forze esterne F e P agenti sul piano medio della trave. Si suppongano note le reazioni
vincolari RA e RB.
y
P
F
A
B
C
D
s
x
RB
RA
38
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Per studiare le caratteristiche della sollecitazione risulta comodo sostituire le forze inclinate F e RB introducendo le componenti parallele ed ortogonali all’asse della trave.
H
F
RB
RBy
V
RBx
Il sistema dato è equivalente a:
y
P
V
H
A
B
C
RBx
D
s
x
RBy
RA
Considerando una sezione generica s, si può supporre un troncamento in tale sezione,
quindi la trave risulta immaginariamente divisa in due parti. Per ripristinare lo stato di
equilibrio è necessario considerare le azioni interne che entrambe le parti si scambiano
attraverso la sezione s. In altre parole, risulta necessario ridurre al baricentro G della sezione esaminata le forze che agiscono sulla parte precedente la sezione e sulla parte seguente la sezione. L’operazione di riduzione delle forze rispetto ad un punto è stata studiata precedentemente.
Dalle condizioni di equilibrio nella sezione risulta:
N1 = −N2
T1 = −T2
M1 = −M2
Le componenti di forze N1 e T1 ed il momento M1 che la parte precedente trasmette alla
parte seguente sono per definizione le caratteristiche della sollecitazione. Oppure si può
dire che le caratteristiche della sollecitazione sono le componenti N2, T2 e il momento
M2 ma cambiati di segno.
39
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
P
V
B
H
A
C
RBx
D
s
RA
RBy
P
B
N1
M1
RBx
D
T1
RBy
V
N2
H
A
C
RA
M2
T2
Per quanto esposto, in una generica sezione s le caratteristiche della sollecitazione possono definirsi nel seguente modo:
•
Lo sforzo normale N è dato dalla somma delle componenti assiali delle forze esterne (attive e reattive) che precedono la sezione (oppure che la seguono ma cambiate di
segno). Le componenti assiali sono parallele all’asse della trave.
•
Lo sforzo di taglio T è dato dalla somma delle componenti trasversali delle forze
esterne (attive e reattive) che precedono la sezione (oppure che la seguono ma cambiate di segno). Le componenti trasversali sono ortogonali all’asse della trave.
•
Il momento flettente M è dato dalla somma dei momenti, rispetto al baricentro della sezione, delle forze esterne (attive e reattive) che precedono la sezione (oppure che
la seguono ma cambiati di segno). Nel caso in cui agiscono momenti applicati concentrati o distribuiti, essi vanno inclusi nella somma.
Quindi considerando “x” coincidente con l’asse della trave e “y” ortogonale a detto asse, si può scrivere:
-
Sforzo Normale
N = ∑ Fxi
i
-
Sforzo di Taglio T = ∑ Fyi
i
-
Momento Flettente M = ∑ M Gi
i
40
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
dove la sommatoria è riferita a tutte le forze (o momenti) che precedono la sezione, oppure che la seguono ma cambiati di segno. Infatti, N, T, ed M possono essere determinate indifferentemente, sia considerando l’azione della parte precedente sulla parte che segue la sezione, sia considerando l’azione della parte seguente sulla parte che precede la
sezione, ma con segni opposti.
y
P
V
A
B
H
C
RA
RBx
x
D
S
RBy
x
L1
L2
L3
Nel caso proposto, le caratteristiche della sollecitazione nella sezione s (posta ad
un’ascissa pari ad x) risultano:
-
Sforzo Normale
N=H
-
Sforzo di Taglio
T = RA − V
-
Momento Flettente
M = R A ⋅ x − V ⋅ (x − L1 )
Per illustrare preliminarmente le variazioni delle azioni interne, si considerano i seguenti valori numerici:
H = 30 kN
V = 40 kN
P = 70 kN
L1 = L2 = L3 = 2 m.
I corrispondenti valori delle reazioni vincolari sono:
RA = 50 kN
RBx = 30 kN
RBy = 60 kN
41
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Diagramma N (kN)
A
C
D
-
30
Diagramma T (kN)
+
50
A
B
10
30
B
D
C
60
-
Diagramma M (kNm)
A
C
D
+
100
Le convenzioni riguardanti i
segni sono indicate nel seguito.
42
120
B
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Convenzioni sui segni delle caratteristiche della sollecitazione
Come si è detto, le caratteristiche della sollecitazione rappresentano gli sforzi interni
provocati in ciascuna sezione dalle forze esterne attive e reattive. Tali sforzi sono il risultato del percorso delle forze all’interno della trave. Le caratteristiche della sollecitazione vengono individuate e denominate in modo da descrivere (piuttosto intuitivamente) l’effetto che producono. Nel caso piano si hanno le sollecitazioni riportate in Figura
18.
Effetti delle caratteristiche della sollecitazione
Trave
N1
N2
Allungamento
Trazione
N1
SFORZO
NORMALE
N2
Accorciamento
Compressione
T1
Scorrimento
SFORZO DI TAGLIO
T2
Incurvamento
M1
M2
MOMENTO FLETTENTE
Figura 18
Facendo riferimento, per semplicità e perché rappresenta un caso molto frequente, ad
una generica trave piana, si indicano nel seguito le convenzioni relative ai segni delle
caratteristiche della sollecitazione:
43
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
a) Sforzo Normale N
Si considera positivo quando sia a sinistra che a destra della sezione “s” agisce una
componente assiale che “esce” dalla sezione (componente assiale “uscente”). In
questo caso lo sforzo normale provoca trazione (allungamento uniforme delle fibre).
Nel caso opposto, sia a sinistra che a destra della sezione “s” le componenti assiali
“entrano” nella sezione, provocando compressione (accorciamento uniforme delle
fibre). In questo caso lo sforzo normale viene considerato negativo.
s
s
G
N
N
G
+
-
Positivo
(Trazione)
elemento
infinitesimo
elemento
infinitesimo
Negativo
(Compressione)
a) Sforzo di Taglio T
La componente di sollecitazione T diretta perpendicolarmente all’asse della trave
provoca uno scorrimento mutuo tra due sezioni contigue. Il taglio nella sezione “s”
si considera positivo se la parte di trave che precede la sezione tende ad alzarsi rispetto alla parte che segue. Mentre se la parte che precede la sezione esaminata tende ad abbassarsi rispetto a quella che segue, il taglio viene considerato negativo.
s
T
s
G
T
lembo inferiore
G
Negativo
+
Positivo
44
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
b) Momento Flettente M
Il momento flettente si considera positivo se incurva la trave con concavità in alto
ossia se risultano compresse (accorciate) le fibre superiori e tese (allungate) le inferiori. Viceversa, se risultano tese le fibre superiori e compresse quelle inferiori, il
momento flettente viene considerato negativo.
Perciò se si determina M considerando le forze che precedono la sezione esaminata,
risultano positivi i momenti destrogiri (orari) e negativi quelli sinistrogiri (antiorari)
e viceversa se si valuta M mediante le forze che seguono la sezione.
M
M
G
G
lembo inferiore
+
Positivo:
fibre superiori compresse
fibre inferiori tese
-
Negativo:
fibre superiori tese
fibre inferiori compresse
Nei casi in cui i tratti di trave risultano verticali o significativamente inclinati è opportuno precisare ulteriormente i criteri per definire la posizione delle fibre assunte
come inferiori (lembo teso se il momento è positivo). Il lembo considerato equivalente all’inferiore si evidenzia mediante una linea tratteggiata collocata in prossimità
della linea d’asse. Con questa indicazione si sottolinea che il momento flettente e
anche lo sforzo di taglio vanno riferiti alla linea tratteggiata intesa come lembo inferiore.
Criteri per la rappresentazione dei diagrammi delle caratteristiche della sollecitazione:
- Per quanto riguarda il momento flettente M i valori positivi si riportano usualmente al di sotto della linea tratteggiata assunta come lembo inferiore, mentre i
45
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
valori negativi si riportano al di sopra dell’asse della trave (lembo superiore Æ
verso positivo dell’asse y). Ricordando che il momento flettente M si considera
positivo quando tende le fibre inferiori e negativo quando tende quelle superiori,
si può dire che il momento si riporta dalla parte delle fibre tese.
- I valori positivi dello sforzo di taglio T usualmente si riportano al di sopra
dell’asse del tratto considerato (verso positivo dell’asse y).
- Per quanto concerne lo sforzo normale N, si può seguire lo stesso criterio indicato per lo sforzo di taglio. Tuttavia questo criterio può essere modificato per chiarezza di rappresentazione.
C
D
C
+
A
B
D
-
B
A
Sforzo normale N
C
D
C
-
D
+
+
A
B
A
Sforzo di taglio T
Momento flettente M
46
B
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.4.2. Relazioni differenziali tra i carichi ripartiti e le caratteristiche della sollecitazione
Per il tracciamento dei diagrammi sono molto utili le relazioni differenziali tra carico
ripartito e caratteristiche della sollecitazione.
Le caratteristiche N, T e M variano generalmente da sezione a sezione, perciò risultano
funzione dell’ascissa “x” della sezione considerata:
N = ϕ1 (x)
T = ϕ2 (x)
M = ϕ3 (x)
Risulta possibile stabilire relazioni differenziali tra carico ripartito – sforzo assiale –
sforzo di taglio – momento flettente.
Si consideri un tratto di una generica trave soggetto ad un carico distribuito p(x) perpendicolare all’asse della trave e ad un carico distribuito assiale n(x) secondo l’asse della trave. Si immagini di isolare un tratto elementare (infinitesimo) della trave, definito
da due sezioni “s” ed “s1” disposte a distanza infinitesima dx. Essendo debole la curvatura della trave, le due facce del tratto elementare possono essere considerate parallele.
• Il tratto elementare dx è soggetto ad un carico distribuito p(x) ortogonale all’asse della trave e ad un carico distribuito assiale n(x) secondo l’asse della trave.
• Sulla faccia corrispondente alla sezione “s” agiscono: il taglio T ed il momento M
(che supponiamo positivi) e lo sforzo normale N (che supponiamo negativo, cioè di
compressione). Questi valori sono equivalenti a tutte le forze esterne che precedono
la sezione “s”.
• Sulla faccia corrispondente alla sezione “s1”, infinitamente vicina alla sezione “s”,
agiscono le caratteristiche della sollecitazione T+dT, M+dM ed N+dN, dove dT, dM
e dN sono rispettivamente le variazioni infinitesime delle caratteristiche T, M ed N
corrispondenti all’incremento dx dell’ascissa x. T+dT, M+dM ed N+dN sono equivalenti a tutte le forze esterne che seguono la sezione “s1”.
47
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
dx
n(x) carico distribuito assiale
(agisce sull’asse della trave)
p(x) carico distribuito normale
all’asse della trave
y
s
s1
asse della trave
x
Trave
O
origine
coordinate
N
N+dN
Diagramma N(x)
T
T+dT
Diagramma T(x)
M
M+dM
Diagramma M(x)
n(x) carico distribuito assiale
(agisce sull’asse della trave)
p(x) carico distribuito normale
all’asse della trave
M
A
N
T+dT
N+dN
x
T
M+dM
s
s1
dx
Le equazioni di equilibrio del tratto elementare forniscono le relazioni differenziali cercate:
∑F
∑F
x
=0
− N + n( x)dx + ( N + dN ) = 0
(1)
y
=0
T − p( x )dx − (T + dT ) = 0
(2)
48
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
∑M
A
 dx 
− M − Tdx + p( x)dx  + ( M + dM ) = 0
 2
=0
(3)
dove:
• n(x)dx è il risultante del carico ripartito assiale distribuito sulla lunghezza infinitesima dx. Essendo dx infinitesimo, è possibile considerare n(x) costante in tale tratto e
pari al valore che assume all’ascissa x (sezione s).
• p(x)dx è il risultante del carico ripartito perpendicolare all’asse distribuito sulla lunghezza infinitesima dx, anche in questo caso è lecito considerare p(x) costante e pari
al valore che assume all’ascissa x (sezione s), il suo risultante sarà pertanto applicato
a metà del tratto dx e cioè a distanza dx/2 dal punto A.
Dalla (1) si ha:
− N + n( x)dx + N + dN = 0
dN
= − n(x)
dx
Æ
Dalla (2) si ottiene:
T − p( x )dx − T − dT = 0
dT
= − p(x )
dx
Æ
Dalla (3) risulta:
dx 2
− M − Tdx + p( x)
+ M + dM = 0
2
dx 2
, si ha
trascurando l’infinitesimo di ordine superiore p( x )
2
− M − Tdx + M + dM = 0
Sostituendo T =
Æ
dM
=T
dx
dT
dM
= − p(x ) si ottiene:
nella espressione
dx
dx
d 2M
= − p( x )
dx 2
49
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Riassumendo:
(A)
dN
= −n(x)
dx
La derivata dello sforzo normale rispetto alla variabile x è uguale al
carico ripartito assiale, cambiato di segno.
La derivata dello sforzo di taglio rispetto alla variabile x è uguale al
(B)
dT
= − p(x )
dx
carico ripartito normale all’asse della trave, cambiato di segno.
Quindi, la derivata del diagramma del taglio (pendenza della curva)
è uguale, ma con segno opposto, al valore del carico ripartito p(x)
alla stessa ascissa.
La derivata del momento flettente rispetto alla variabile x è uguale
(C)
allo sforzo di taglio. Perciò, la derivata del diagramma dei momenti
dM
=T
dx
flettenti (pendenza) è uguale al valore del taglio T alla stessa ascissa.
Dalle tre espressioni differenziali (A), (B) e (C) si ricavano le caratteristiche della sollecitazione nella generica sezione “s” di ascissa xs:
xs
N s = − ∫ n( x)dx + C 0
0
xs
Ts = − ∫ p ( x )dx + C1
0
xs
M s = ∫ Tdx + C2
0
le costanti C0, C1 e C2 si determinano in base alle condizioni iniziali (rappresentano le
caratteristiche della sollecitazione all’origine dell’asse x).
50
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Osservazioni
1) Nei tratti scarichi (p(x)=0) il taglio T è costante o nullo ed M varia linearmente o è
costante. Infatti con p(x)=0 risulta:
Ts = C1 = costante o nullo
xs
M s = ∫ C1dx + C2 = C1 x s + C2
0
Il momento flettente è costante soltanto se è nullo lo sforzo di taglio
2) Nei tratti soggetti a carichi distribuiti (p(x)≠0) T ed M variano con leggi continue:
•
se p(x)=costante
Ts varia con legge lineare (primo grado)
Ms varia con legge di secondo grado (parabolica)
•
se p(x) varia con legge lineare
Ts varia con legge di secondo grado
Ms varia con legge di terzo grado
Si osservi che la funzione del taglio cresce di un grado rispetto al carico ripartito, e che
la funzione del momento flettente cresce di un grado rispetto al taglio e quindi di due
rispetto al carico ripartito.
3) Nelle sezioni in cui lo sforzo di taglio si annulla, il momento flettente risulta massimo (derivata prima nulla, derivata seconda negativa) o minimo (derivata prima nulla,
derivata seconda positiva).
4) Se in un tratto della trave il taglio è nullo (T=0), il momento flettente è costante.
5)
Se lo sforzo di taglio è diverso da zero (T≠0), esiste sempre il momento flettente
(può annullarsi in qualche sezione ma non in un tratto di lunghezza finita).
5) La componente trasversale (ortogonale all’asse della trave) di un carico concentrato
P produce, oltre ad una discontinuità nel diagramma del taglio, un punto angoloso nel
diagramma del momento flettente.
51
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Applicazione: Trave appoggiata con carico concentrato
Calcolo delle reazioni e delle caratteristiche della sollecitazione - Diagrammi
Si consideri una trave vincolata agli estremi e soggetta all’azione di un carico concentrato P normale all’asse della trave, come indicato in figura.
y
P
1/3L
2/3L
s
A
B
L/2
x
s
L
¾ Determinazione delle reazioni vincolari
RAx è nulla perché non sono presenti altre forze orizzontali.
RAy si determina mediante l’equilibrio dei momenti rispetto al punto B, ipotizzando i
versi indicati nella sottostante figura, si ha:
2
− RAy ⋅ L + P ⋅ L = 0
3
ΣMB = 0
RAy =
2
P
3
RB si ricava tramite l’equilibrio dei momenti rispetto al punto A:
1
RB ⋅ L − P⋅ L = 0
3
ΣMA = 0
RB =
1
P
3
P
P
1/3L
2/3L
1/3L
A
B
RAy
RB
A
RAy = 2/3P
L
52
2/3L
B
RB= 1/3P
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
¾ Caratteristiche della sollecitazione nella sezione di mezzeria (xs = L/2)
Si sceglie l’origine del sistema di riferimento in A e si stabilisce il verso di percorrenza
da A verso B, perciò “x” è l’ascissa misurata a partire da A. La trave è rappresentata dal
suo asse.
Poiché le forze attive e reattive sono normali all’asse della trave ed inoltre sono contenute in un piano che contiene uno degli assi principali d’inerzia della sezione (sollecitazione piana), esistono soltanto sforzo di taglio Ts e momento flettente Ms.
Essendo tutte le forze agenti perpendicolari all’asse della trave la componente secondo
l’asse é nulla, cioè N = 0.
Si consideri adesso la sezione di mezzeria, cioè xs=L/2. La riduzione al baricentro della
sezione del sistema delle forze attive e reattive che agiscono sulla parte che precede la
sezione “s” fornisce:
T1 =
2
1
P−P=− P
3
3
M1 =
2
1
1
1
P ⋅ L − P ⋅ L = PL
3
2
6
6
T1 = −
1
P
3
M1 =
1
PL
6
T1 e M1 rappresentano l’azione che il corpo 1 (parte della trave che precede la sezione
considerata) trasmette al corpo 2 (parte della trave che segue la sezione considerata).
La riduzione al baricentro della sezione del sistema delle forze attive e reattive che agiscono sulla parte che segue la sezione “s” fornisce:
T2 =
1
P
3
M2 = −
1
1
1
P ⋅ L = − PL
3 2
6
M2 = −
1
PL
6
T2 e M2 rappresentano l’azione che il corpo 2 trasmette al corpo 1.
53
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
L/2
L/2
P
1/3L
2/3L
s
A
B
s
x
1/3 P
2/3 P
P
1/3L
A
1/6L
corpo 1
s
s
s
s
B
corpo 2
1/3 P
2/3 P
Riduzione al baricentro della sezione “s”
T1 = -1/3 P
M1
s
s
s
s
T2
T1
M1 = 1/6 PL
M2
T2 = 1/3 P
M2 = - 1/6 PL
T1 = - T 2
P
M1 = - M2
Equilibrio
corpo 1
Equilibrio
corpo 2
T2 M2
2/3 P
M1 T1
1/3 P
I valori delle caratteristiche della sollecitazione nella sezione “s” di mezzeria sono M1 e
T1, oppure M2 e T2 con segni cambiati, quindi:
Ts = −
1
P
3
Ms =
1
PL
6
54
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
¾ Leggi di variazione delle caratteristiche della sollecitazione - DIAGRAMMI
• Sforzo di taglio Ts
In questo caso risulta definito come il risultante di tutte le forze esterne (attive e reattive) che precedono la sezione “s”. Per una generica distanza “xs” dall’origine si ha:
Ts =
2
P
3
Ts = −
per xs < L/3
1
P
3
per xs > L/3
P
1/3L
2/3L
B
A
s
s
1/3P
2/3P
Si considera positivo il taglio nella
+
sezione “s” se la parte della trave che
-
precede “s” tende ad alzarsi rispetto
alla parte che segue
P
+ 2/3P
A
+
B
-
- 1/3P
Diagramma dello
sforzo di taglio Ts
In corrispondenza di un carico concentrato il diagramma del taglio evidenzia un salto
pari al valore del carico. Il valore assunto dallo sforzo di taglio va ricercato immediatamente a sinistra e immediatamente a destra della sezione sollecitata da un carico concentrato.
55
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
• Momento flettente Ms
Per una generica sezione “s” a distanza “xs” dall’origine, il momento flettente Ms, definito come il momento risultante rispetto al baricentro della sezione di tutte le forze (attive e reattive) che agiscono sulla parte della trave che precede la sezione, vale:
Ms =
2
P ⋅ xs
3
Ms =
2
1
1
P ⋅ xs – P ⋅ (xs − L) = P ⋅ (L − xs)
3
3
3
per xs ≤ L/3
per xs ≥ L/3
P
1/3L
2/3L
B
A
s
s
1/3P
2/3P
L/2
L/2
Diagramma del
+
Mmax=2/9 PL
momento flettente Ms
ML/2=1/6 PL
+
Il momento flettente si considera positivo
quando tende le fibre inferiori della trave
In corrispondenza della sezione in cui il taglio inverte il segno, il momento flettente assume un valore massimo, e il diagramma di M inverte la pendenza:
per xs =
1
L
3
si ha
Mmax =
2
PL
9
Il valore del momento in mezzeria (xs = L/2) vale:
ML/2 =
1
1
1
P ⋅ (L - L) = P L
3
2
6
56
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Applicazione: Trave appoggiata con carico ripartito uniforme
Calcolo delle reazioni vincolari e delle caratteristiche della sollecitazione - Diagrammi
Si consideri una trave appoggiata agli estremi e soggetta ad un carico ripartito uniforme
“p” normale all’asse della trave.
Le forze attive e reattive risultano perpendicolari all’asse della trave ed inoltre sono
contenute in un piano che contiene uno degli assi principali di inerzia della sezione,
quindi esistono soltanto le caratteristiche della sollecitazione T ed M, cioè taglio e momento flettente, infatti, essendo tutte le forze agenti normali all’asse della trave la componente secondo l’asse é nulla, cioè N = 0.
y
p
A
deformata
B
x
L
Si sceglie l’origine del sistema di riferimento in A e si stabilisce il verso di percorrenza
da A verso B, quindi x è l’ascissa misurata a partire da A.
¾ Determinazione delle reazioni vincolari
Ai fini della ricerca delle reazioni vincolari è lecito ridurre il carico ripartito al proprio
risultante, in questo caso Q = p⋅L applicato in mezzeria. Quindi, per le reazioni vincolari
si ha:
RAx = 0 perché non sono presenti altre forze orizzontali.
RAy si determina mediante l’equilibrio dei momenti rispetto al punto B:
ΣMB = 0
1
− RAy ⋅ L + p⋅L ⋅ L = 0
2
RAy =
1
p⋅L
2
RB si ricava tramite l’equilibrio dei momenti rispetto al punto A:
57
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
ΣMA = 0
1
RB ⋅ L − p⋅L ⋅ L = 0
2
RB =
1
p⋅L
2
¾ Caratteristiche della sollecitazione
Le caratteristiche della sollecitazione in una generica sezione della trave si possono determinare:
1) Applicando direttamente le definizioni di sforzo di taglio e di momento flettente.
2) Mediante l’integrazione delle relazioni differenziali tra le caratteristiche della
sollecitazione ed i carichi ripartiti.
In generale i valori dello sforzo di taglio T e del momento flettente M dipenderanno dalla posizione della sezione considerata. Le funzioni T = ϕ1 (x) ed M = ϕ2 (x), che esprimono i valori delle caratteristiche della sollecitazione al variare dell’ascissa “x”, vengono rappresentate graficamente dai corrispondenti diagrammi.
Metodo (1). Calcolo diretto dello sforzo di taglio e del momento flettente.
•
Lo sforzo di taglio Ts in una generica sezione “s” è dato dal risultante secondo l’asse
“y” di tutte le forze (attive e reattive) che precedono la sezione. Il taglio si considera
positivo se la parte della trave che precede “s” tende ad alzarsi rispetto alla parte che
segue.
+
•
-
Il momento flettente nella sezione “s” è definito dal momento risultante rispetto al
baricentro della sezione di tutte le forze (attive e reattive) che precedono la sezione.
Il momento flettente si considera positivo se risultano tese le fibre inferiori e compresse le superiori.
+
-
Per una generica sezione “s” a distanza xs dall’origine (appoggio A) lo sforzo di taglio
vale:
58
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Ts = RA − p⋅xs
cioè Ts = p (
Æ
Ts =
1
p⋅L − p⋅xs
2
1
L − xs) espressione di una retta
2
xs
A
B
s
RA = 1/2pL
RB = 1/2pL
L
Qs
Qs : risultante dei carichi
ripartiti nel tratto che va
1/2pL
Ts = 1/2pL - p xs
dall’origine alla sezione “s”
xs
Qs = p xs
Diagramma dello sforzo di taglio Ts
x=0
T = 1/2 pL
+
-
x= L
T = - 1/2 pL
+
-
Lo sforzo di taglio ha andamento lineare con massimo (in valore assoluto) agli estremi e
uguale a pL/2 ed è nullo in mezzeria (x = L/2).
59
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Il diagramma del taglio è emisimmetrico rispetto alla sezione di mezzeria, ciò è dovuto
al fatto che i carichi e le reazioni sono simmetrici rispetto alla mezzeria.
Per una generica sezione “s” a distanza xs dall’origine (appoggio A) il momento flettente, definito come il momento risultante di tutte le forze (attive e reattive) che agiscono
sulla parte della trave che precede la sezione, vale:
Ms = RA ⋅ xs − p⋅xs ⋅
cioè Ms =
1
xs
2
Æ
Ms =
1
1
p⋅L⋅xs − p⋅xs2
2
2
1
p (L xs − xs2) espressione di una parabola
2
xs
p
A
B
s
RA = 1/2pL
RB = 1/2pL
L
Qs
Ms
p
Nota: il momento si considera
1/2pL
positivo quando tende le fibre
xs /2
inferiori della trave
xs
Diagramma del momento flettente Ms
+
per x = L/2
2
Mmax = 1/8 pL
pendenza
negativa
pendenza
positiva
La legge di variazione del momento flettente è parabolica con massimo pari a
1 2
pL in
8
mezzeria. Si osservi che lo sforzo di taglio si annulla in mezzeria dove il momento è
60
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
massimo. A taglio positivo corrisponde pendenza negativa del diagramma del momento
(vale a dire momento crescente), viceversa, a taglio negativo corrisponde pendenza positiva (vale a dire momento decrescente).
Il diagramma del momento può essere tracciato graficamente in diversi modi.
Metodo (1). Tracciato grafico del diagramma parabolico di 2° grado
Il punto C in mezzeria è definito dalla ordinata 2·Mmax.
Si dividono i segmenti AC e CB in “n” parti uguali (nella figura n = 5) e si uniscono tra
loro i punti divisori corrispondenti: 1 con 1’; 2 con 2’; 3 con 3’; 4 con 4’; 5 con 5’. Queste rette rappresentano delle tangenti alla parabola. La curva ottenuta come inviluppo
delle tangenti è la legge parabolica di 2° grado che rappresenta l’andamento del momento flettente.
Metodo (2). Applicazione delle relazioni differenziali tre p, T ed M.
Le espressioni delle variazioni dello sforzo di taglio e del momento flettente si possono
ricavare mediante l’integrazione delle relazioni differenziali:
dT
= − p( x )
dx
dM
=T
dx
Per integrazione del carico ripartito si ha
xs
Ts = − ∫ p( x )dx + TA
0
dove TA rappresenta la costante di integrazione ed è la forza di taglio nella sezione di
origine (x=0).
Nel caso in esame p(x) = p = costante quindi risulta:
61
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
xs
Ts = −p ∫ dx + TA = − px s +
0
pL
2
cioè
L

Ts = p − x s 
2

che è la stessa espressione ottenuta mediante l’applicazione diretta della definizione di
T.
La pendenza in un punto del diagramma del taglio è data, a meno del segno,
dall’intensità locale del carico ripartito p; in questo caso la pendenza del diagramma T è
costante.
Per integrazione dello sforzo di taglio si ha:
xs
M s = ∫ Tdx + M A
0
essendo MA il momento nella sezione di origine (x=0) che in questo caso è nullo.
Sostituendo l’espressione di T determinata precedentemente si ha:
xs
x
x
s
s
L
L

M s = ∫ p − x dx = ∫ p dx − ∫ pxdx
2

0 2
0
0
essendo p costante risulta:
Ms = p
x
(
x
s
x s2 p
L s
L
dx
p
xdx
p
−
=
x
−
p
= Lx s − x s2
s
∫
2 ∫0
2
2
2
0
)
che è la stessa espressione ottenuta mediante la definizione di M (metodo 1).
Poiché la derivata del momento rispetto ad x è uguale al taglio, la pendenza in un punto
del diagramma del momento rappresenta la forza di taglio in quel punto.
Inoltre essendo
xs
M s = ∫ Tdx + M A
0
il momento in una sezione si può ottenere sommando all’integrale (area) del diagramma
dello sforzo di taglio eventuali coppie concentrate e distribuite; ad esempio per la mezzeria si ha:
62
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Diagramma dello sforzo di taglio Ts
Area = valore del
1/2 pL
momento in mezzeria
+
sezione di mezzeria
L/2
Mmax = momento flettente in mezzeria = area del diagramma di taglio dall’origine
 pL L  1
alla sezione di mezzeria, cioè M max = 
 (area del triangolo che rap 2 22
presenta lo sforzo di taglio)
Il momento è massimo dove lo sforzo di taglio si annulla (sezione di mezzeria), poiché
dove il taglio è nullo la tangente del momento è orizzontale, quindi il momento presenta
un punto di massimo o minimo.
63
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Applicazione: Trave appoggiata con carico ripartito lineare
Caratteristiche della sollecitazione - Diagrammi
Si consideri una trave appoggiata agli estremi e soggetta ad un carico ripartito crescente
con legge lineare da zero al valore massimo p0.
y
p(x) = p0 x/L
p0
A
x
s
B
L
Considerando il sistema di riferimento indicato in figura (origine nel punto A e ascissa
“x” misurata lungo l’asse della trave), la legge di variazione del carico p(x) risulta:
p(x) =
p0
p(x)
p0
x
L
A
B
x
dove p0 è il carico unitario massimo per x=L
L
Inoltre, il risultante Q del carico ripartito che precede una sezione di ascissa x vale
Q=
p x2
1
1 p
⋅ p( x ) ⋅ x = ⋅ 0 x ⋅ x = 0
2
2 L
2L
x
Q = area del triangolo che ha per base x
p(x)
p
e per altezza il valore p(x) = 0 x
L
Q dista
p0
Q
x
dalla sezione considerata.
3
x/ 3
Le reazioni dei vincoli si possono determinare mediante le equazioni di equilibrio e risultano:
RA =
p0L
6
RB =
p0L
3
64
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Le caratteristiche della sollecitazione si possono ottenere: (1) direttamente applicando le
definizioni di sforzo di taglio e di momento flettente nella generica sezione “s” oppure
(2) mediante l’integrazione delle relazioni differenziali tra le caratteristiche della sollecitazione e i carichi ripartiti.
Si osservi che non essendoci forze (attive e/o reattive) agenti parallelamente all’asse
della trave, lo sforzo normale è nullo.
Metodo (1). Calcolo diretto dello sforzo di taglio e del momento flettente.
Per stati di sollecitazione piani, lo sforzo di taglio T in una sezione generica “s” è uguale al risultante delle componenti verticali di tutte le forze (attive e reattive) che precedono la sezione. Quindi nella sezione “s” corrispondente all’ascissa “xs” , si ha:
Ts = RA − Qs
p 0 x s2
Dove Qs è il risultante del carico ripartito che precede la sezione “s” e vale Q s =
2L
xs
Ts = RA − Qs =
 L x2 
p 0 L p 0 x s2
−
= p 0  − s 
6
2L
 6 2L 
A
L

 sforzo di taglio
Ts = p 0  −

6
2L


x s2
Ts
Qs
RA
xs /3
Si osserva che lo sforzo di taglio varia con legge di secondo grado.
Per stati di sollecitazione piani, il momento flettente Ms nella sezione generica “s” è dato dal momento risultante rispetto al baricentro di “s” di tutte le forze (attive e reattive)
che precedono la sezione considerata.
Il momento del carico ripartito rispetto al baricentro di “s” si ottiene moltiplicando il carico risultante Qs per la sua distanza da “s” che è
xs
. Il momento della reazione RA si
3
ottiene moltiplicando RA per la sua distanza da “s” che vale xs.
Quindi il momento flettente nella sezione “s” risulta:
Ms = RA · xs − Qs ·
xs
3
65
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
p 0 x s2
p0L
e Qs =
Sostituendo RA =
6
2L
Ms =
p
p0L
p x2 x
⋅ xs − 0 s ⋅ s = 0
6
6
2L 3
Ms =
p0
6
risulta:

x3 
 Lx s − s 

L 


x3 
 Lx s − s  momento flettente

L 

L’andamento del momento flettente segue una legge di terzo grado.
L’ascissa “x0” corrispondente al massimo momento flettente si ottiene dalla condizione
Ts=0 (la sezione in cui lo sforzo di taglio si annulla presenta il massimo, in valore assoluto, momento flettente)
 L x2 
Ts = p0  − 0  = 0
 6 2L 
Ts = 0
da cui x 0 =
L x 02
=
6 2L
x 02 =
L2
3
L
≅ 0.5773L ascissa di massimo momento flettente
3
essendo Ms =
p0
6

x3 
 Lx s − s  , per x s = x 0 = L si ha:

L 
3

Msmax ≅ 0.06415 p0L2 momento flettente massimo
Metodo (2). Applicazione delle relazioni differenziali tra carico ripartito, sforzo di ta-
glio e momento flettente.
Precedentemente sono state dedotte le seguenti relazioni differenziali tra carico ripartito,
sforzo di taglio e momento flettente:
dT
= − p( x )
dx
dM
=T
dx
d 2M
= − p( x )
dx 2
Nota la legge di variazione del carico ripartito p(x), per integrazione si ottengono lo
sforzo di taglio Ts ed il momento flettente Ms.
Quando non agiscono carichi concentrati (oppure in ogni tratto compreso tra carichi
concentrati) è possibile determinare Ts e Ms mediante l’integrazione delle relazioni differenziali, quindi:
xs
Ts = − ∫ p( x )dx + TA
sforzo di taglio nella sezione “s”
0
66
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
xs
M s = ∫ Tdx + M A
momento flettente nella sezione “s”
0
dove TA ed MA sono le costanti di integrazione che si determinano conoscendo le condizioni iniziali.
Nel caso della trave appoggiata con carico ripartito triangolare si ricava:
a) Sforzo di taglio nella sezione generica “s”
essendo p(x) =
p0
x
L
xs
p0
p
xdx + TA = TA − 0
L
0 L
Ts = − ∫
xs
∫ xdx = TA −
0
p 0 x s2
2L
( ∫ xdx =
x2
)
2
dove TA è il valore dello sforzo di taglio per x = 0 (appoggio A) che è la reazione RA
RA =
Ts =
p0L
, quindi si ha:
6
 L x2 
p 0 L p 0 x s2
−
= p 0  − s  taglio nella generica sezione “s”
6
2L
 6 2L 
b) Momento flettente nella sezione generica “s”
xs
M s = ∫ Tdx + M A
0
dove MA è il valore del momento flettente per x = 0 (appoggio A) che è nullo (MA =
0).
 L x2 
M s = ∫ p 0  − S dx
 6 2L 
0


xs
x
x
p L s
p s
M s = 0 ∫ dx − 0 ∫ x 2 dx
6 0
2L 0
Ms =
p0L
p x3
xs − 0 s
6
2L 3
Ms =
p0 
x3 
 Lx s − s  momento flettente nella generica sezione “s”
6 
L 
( ∫ xdx =
x2
;
2
67
2
∫ x dx =
x3
)
3
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Diagrammi delle caratteristiche della sollecitazione
68
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Applicazione: Trave incastrata con carico uniformemente ripartito
Caratteristiche della sollecitazione - Diagrammi
Si consideri la trave incastrata in A e soggetta ad un carico uniformemente ripartito p
y
p
MA
A
E
s
RAy
x
deformazione
L
Le componenti della reazione d’incastro valgono:
RAx = 0;
M A = −p
RAy = pL;
L2
2
• Lo sforzo normale è nullo.
• Sforzo di taglio
Per una generica sezione “s” a distanza xs dall’origine (punto A) lo sforzo di taglio risulta uguale al risultante di tutte le forze esterne (attive e reattive) che precedono la sezione esaminata.
Ts = RAy – pxs = pL − pxs
Per un carico p uniforme il taglio risulta funzione
di primo grado in x.
Per xs = 0 (punto A)
TA = pL
Per xs = L (punto E)
TE = 0
Lo sforzo di taglio è sempre positivo poiché la parte precedente la sezione tende ad alzarsi rispetto alla parte seguente.
69
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
pL
Diagramma sforzo di taglio T
+
+
• Momento flettente
Il momento flettente è definito come il momento risultante, rispetto al baricentro della
sezione considerata, di tutte le forze esterne (attive e reattive) che agiscono sulla parte di
trave che precede la sezione, in questo caso occorre tenere conto della presenza del
momento di incastro MA. Per una generica sezione “s” a distanza xs dall’origine, il momento flettente vale:
M s = M A + R Ay ⋅ x s − px s ⋅
xs
2
Ms = −
px 2
pL2
+ pLx s − s
2
2
Variazione di secondo grado (parabolica). La funzione momento cresce di un grado rispetto al taglio.
Per xs = 0 (punto A)
MA = −
Per xs = L (punto E)
ME = 0
Per xs = L/2 (mezzeria trave)
M=−
pL2
2
L p L2
pL2
pL2
+ pL −
=−
2 2 4
8
2
Il momento si mantiene sempre negativo comprimendo il lembo inferiore (linea tratteggiata). Essendo il taglio positivo e decrescente, la pendenza del momento è sempre negativa e decrescente. Quindi la concavità è rivolta verso l’alto.
pL2
8
pL
2
2
A
Diagramma momento flettente M
-
E
L/2
70
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Applicazione: Trave rettilinea soggetta a diversi tipi di carico
Diagrammi delle sollecitazioni
Si consideri la trave appoggiata nei punti A e B e soggetta a diversi carichi (ripartiti e
concentrati).
P1
α
p(x) = p0 x/L
q
β
M0
1
A
RA
γ
w
2
B
δ
ϕ
x
a
P2
p0
L
q:
carico inclinato uniformemente ripartito
p(x):
carico ripartito crescente con legge lineare
w:
carico uniformemente ripartito
RB
b
L’asse della trave e le forze agenti sono contenute in un piano che contiene anche un
degli assi principali d’inerzia della sezione, quindi si avranno solo sforzo normale N,
sforzo di taglio T e momento flettente M.
I carichi agenti sono:
­
un carico inclinato uniformemente ripartito q (nello sbalzo che precede l’appoggio
A);
­
un carico verticale ripartito p, crescente con legge lineare da zero fino al valore
massimo p0, nel tratto AB;
­
un carico concentrato P1 inclinato dell’angolo β rispetto all’asse della trave, applicato nella mezzeria del tratto AB (punto 1);
­
una coppia M0 applicata nella mezzeria del tratto AB (punto 1);
­
un carico verticale uniformemente ripartito w (agente sullo sbalzo che segue
l’appoggio B);
­
un carico concentrato P2 inclinato dell’angolo γ rispetto all’asse della trave, applicato nel punto 2.
71
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Le reazioni vincolari sono:
­
la reazione del carrello in A, parallela all’asse del carrello (inclinato rispetto all’asse
della trave di un angolo δ);
la reazione della cerniera in B, inclinata di un angolo ϕ non noto a priori.
­
Per il calcolo delle caratteristiche della sollecitazione è opportuno scomporre tutte le
forze (attive e reattive) agenti sulla struttura secondo la direzione assiale (normale alla
sezione), cioè parallela all’asse della trave, e secondo la direzione trasversale, cioè perpendicolare all’asse della trave. Le prime generano sollecitazione di sforzo normale, le
seconde generano sollecitazioni di taglio e di flessione.
Decomposizione delle forze inclinate in:
- componenti assiali
- componenti normali all’asse
α
q cosα
q
=
q senα
+
a
a
a
P2
P1 senβ
P1
β
γ
P1 cosβ
P2 cosγ
P2 senγ
RA cosδ
RA
δ
RB cosϕ
RB senϕ
RA senδ
ϕ
RB
72
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Componenti assiali delle forze
q cosα
RA cosδ
P1 cosβ
RB cosϕ
1
B
A
a
P2 cosγ
2
L
b
Componenti delle forze normali all’asse della trave
(componenti trasversali)
P1 senβ
p(x) = p0 x/L
P2 senγ
p0
M0
q senα
w
1
A
RA senδ
a
2
B
RB senϕ
L
b
Il sistema di carichi agenti considerato è molto generale e permette una adeguata comprensione della determinazione delle caratteristiche della sollecitazione.
Nelle seguenti figure sono indicate le componenti delle forze agenti (attive e reattive) e i
relativi diagrammi delle sollecitazioni.
73
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Componenti assiali delle forze
ÎSforzo normale
Componenti delle forze normali all’asse della trave (componenti trasversali)
Ï Sforzo di taglio
74
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Componenti delle forze normali all’asse della trave (componenti trasversali)
Momento flettente
75
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Riepilogo diagrammi delle sollecitazioni
76
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Si riporta nel seguito un esempio numerico.
p0 = 3 t/m
P1=5.2t
α = 45°
p(x) = x/2
q = 2 t/m
β=
60°
M0 = 3tm 1
A
RA=12.18 t
γ
P2 = 2.4 t
γ = 45°
w = 1 t/m
2
B
0.8 m
δ = 45°
ϕ = 66°11
RB=12.05 t
x
a=2m
L= 6 m
b = 1.6 m
Decomposizione delle forze inclinate
α = 45°
2 t/m
=
4.5 t
qt = 1.41 t/m
ql = 1.41 t/m
+
P2
P1
1.7 t
γ = 45°
β = 60°
1.7 t
2.6 t
4.88 t
8.61 t
RA
8.61 t
11.02 t
RB
ϕ = 66°11
δ = 45°
77
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Componenti assiali delle forze
RA cosδ
= 8.61 t
ql = 1.41 t
A
a=2m
P1 cosβ
= 2.6 t
RB cosϕ
= 4.88 t
1
B
L= 6 m
P2 cosγ
= 1.7 t
2
0.8 m
b = 1.6 m
Componenti delle forze normali all’asse della trave
(componenti trasversali)
P1 senβ
= 4.5 t
P2 senγ
= 1.7 t
p0 =
3 t/m
p(x) = x/2
qt = 1.41 t
A
M0 = 3 tm 1
RA senδ
= 8.61 t
a=2m
B
RB senϕ
= 11.02 t
L= 6 m
w = 1 t/m
2
0.8 m
b = 1.6 m
Le componenti assiali delle forze generano sforzo normale, mentre quelle trasversali
generano sforzo normale e momento flettente. I relativi diagrammi sono riportati nella
figura seguente.
78
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Riepilogo diagrammi delle sollecitazioni
tm
tm
tm
tm
79
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.4.3. Caratteristiche della sollecitazione per travi costituite da
tratti inclinati e orizzontali
Considerando la definizione relativa alle direzioni delle caratteristiche della sollecitazione (componenti del risultante in un particolare sistema di riferimento), si osserva che
se la struttura include tratti (travi) ad asse inclinato gli sforzi normali e di taglio devono
essere valutati rispetto agli assi locali di ogni singolo tratto.
y
y
x’
y’
x’
A
D
E
x”
y’
x
B
D
y”
x
B
A
a) Due tratti
b) Tre tratti
Connessioni rigide - continuità
Ad esempio, nel caso a) nel tratto AD lo sforzo normale N (componente assiale del risultante) ha la direzione dell’asse AD, mentre lo sforzo di taglio T ha la direzione della
normale all’asse AD. Si osservi che il vettore momento (momento flettente) risulta
sempre ortogonale al piano della rappresentazione e perciò non cambia al variare
dell’orientamento degli assi locali.
Per la valutazione delle caratteristiche della sollecitazione si procede analizzando ciascun tratto. All’inizio di ogni tratto dovrà tenersi conto della sollecitazione presente nel
punto i origine degli assi locali, cioè sarà considerata la riduzione rispetto a tale punto di
tutte le forze attive e reattive che agiscono sulla parte precedente della struttura.
y
MD
x
ND
D
B
ND - TD - MD
Riduzione al punto D di tutte le
forze esterne (attive e reattive)
TD
che agiscono sul tratto AD
A
80
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
I valori di ciascuna caratteristica della sollecitazione in corrispondenza di ogni sezione
si rappresentano mediante diagrammi che hanno come linea di riferimento gli assi geometrici di ciascun tratto di trave.
p
D
B
A
+
+
D
B
Digramma dello Sforzo Normale N
tra
zio
ne
trazione
A
D
B
-
Diagramma dello Sforzo di Taglio T
+
A
D
B
Diagramma del Momento Flettente M
+
+
A
+
+
81
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
In corrispondenza del punto angoloso (nodo D) della linea d’asse il momento flettente
assume un valore unico. Perciò tracciato il diagramma per il tratto AD fino a D, si prosegue ribaltando il valore del momento flettente sulla perpendicolare al tratto successivo
DB.
D
B
A
82
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Applicazione: Trave a ginocchio per rampa di scala
Caratteristiche della sollecitazione.
Con riferimento alla trave a ginocchio riportata in figura, si determinano le caratteristiche della sollecitazione e si tracciano i relativi diagrammi.
4.50 m
2.15 m
2.55 m
1.5 m
a)
pianta scala
A
0.30
2.55 m
b)
0.17
gradini
4.50 m
a) Scala in cemento armato con rampa a solettone a ginocchio
b) Schema strutturale
Analisi dei carichi
Peso proprio soletta in c.a.
~ 7.5 kN/m
Peso proprio gradini
~ 2.5 kN/m
Sovraccarico (4 kN/m2 x 1.5 m)
~ 6.0 kN/m
Carico uniformemente ripartito
q ≅ 16 kN/m
(riferito alla proiezione orizzontale)
83
D
B
2.00 m
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Carico - Schema strutturale - Reazioni
q = 16 kN/m
A
2.55 m
α
RA = 52 kN
B
D
RB = 52 kN
4.50 m
RA = RB =
α = arctg
2.00 m
q ⋅ 6.5
= 52 kN
2
2.55
≅ 29°54
4.50
cos α ≅ 0.870
sen α ≅ 0.493
Per il calcolo delle caratteristiche della sollecitazione è opportuno decomporre le forze
agenti (attive e reattive) secondo le direzioni parallela e normale all’asse del tratto considerato, si operano quindi le seguenti scomposizioni:
a) Decomposizione di RA secondo le direzioni parallela e perpendicolare all’asse del
tratto AD (assi x’ e y’)
asse tratto AD (asse x’)
RAx’ = 25.64
RA = 52
α RAy’ = 45.24
α
R Ax' = 52 ⋅ senα ≅ 25.64
R Ay' = 52 ⋅ cosα ≅ 45.24
84
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
b) Riduzione al baricentro della sezione D dell’insieme di forze che agiscono sul tratto
AD. Sollecitazione nella sezione D.
q = 16 kN/m
72 kNm
D
B
20 kN
52 – 16 · 4.5 = – 20 kN
52 ⋅ 4.5 −
16 ⋅ 4.52
= 72 kN
2
c) Riduzione al baricentro della sezione D dell’insieme di forze che agiscono sul tratto
DB e decomposizione secondo le direzioni parallela e perpendicolare al tratto AD (d).
q = 16 kN/m
asse tratto AD
(asse x’)
A
α
9.86 kN
72 kNm
D
20 kN α
17.40 kN
20 kN
c)
d)
e) Scomposizione del carico ripartito q. Componenti trasversale ed assiale del carico uniforme q nel tratto AD:
p = q cos2α (componente trasversale)
p = 16 cos2(29°54) ≅ 12.11 kN/m
n = q senα cosα (componente assiale) n = 16 sen(29°54) cos(29°54) ≅ 6.863
kN/m
NB: p è ottenuto moltiplicando q per cos2α, e non semplicemente per cos α, per tener
conto dell’incremento di lunghezza della trave che in proiezione orizzontale è lunga
4.50 m mentre in vera forma è lunga 4.50 m/cos α..
85
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
A
componente
trasversale
p = q cos 2 α
n = q cosα senα
α
p
componente
assiale
n
D
x’
¾ Caratteristiche della sollecitazione
• Sforzo Normale
Sul tratto DB non esistono
Componenti assiali che agiscono sul tratto AD
componenti assiali.
RAx’ =
25.64
Lo sforzo normale è nullo
y’
lungo tutto il tratto DB
A
n=
s
5 .1
72
6 .8
63
kN
/
m
m
y
9.86 kN
D
x
D
x’
B
2m
Considerando gli assi x’y’ con origine in A, la funzione sforzo normale nel tratto AD
vale
N(x’) = 25.64 – nx’ = 25.64 – 6.863x’ (andamento lineare)
Per x’ = 0 (punto A)
N = 25.64 kN
Per x’ = 2.586 (mezzeria tratto AD)
N = 25.64 – 6.863 · 2.586 ≅ 7.89 kN (tra-
zione)
Per x’ = 5.172 (punto D)
N = 25.64 – 6.863 · 5.172 ≅ − 9.86 kN (compres-
sione)
Passando lo sforzo normale da valori positivi a valori negativi, esiste un punto di ascissa
x ' in cui N si annulla. Lo sforzo normale si annulla per x ' ≅ 3.736 m (punto E)
86
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
x' =
infatti N(x’) = 25.64 – 6.863 x ' = 0 Æ
25.64
≅ 3.736 m
6.863
Nel tratto DB lo sforzo normale è ovunque nullo.
Con i valori ricavati precedentemente si può tracciare il diagramma
• Sforzo di Taglio
Componenti trasversali che
Componenti trasversali che
agiscono sul tratto AD
agiscono sul tratto DB
y’
p=
A
RAy’ =
45.24
12.
11
k
N/m
y
q = 16 kN/m
s
5.1
72 kNm
72
m
17.40
72 kNm
B
D
D
s
x’
20 kN
2m
In una generica sezione “s” del tratto AD, lo sforzo di taglio risulta:
87
x
RB =
52 kN
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
T(x’) = 45.24 – px’ = 45.24 – 12.11x’ (variazione lineare)
Per x’ = 0 (punto A)
T = 45.24 kN
Per x’ = 2.586 (mezzeria tratto AD)
T = 45.24 – 12.11 · 2.586 ≅ 13.92 kN
Per x’ = 5.172 (punto D)
T = 45.24 – 12.11 · 5.172 ≅ - 17.40 kN
Lo sforzo di taglio si annulla per x ' ≅ 3.736 (punto E)
infatti T( x ' ) = 45.24 – 12.11 x ' = 0 x ' =
45.24
≅ 3.736 m.
12.11
Per il tratto DB si considerano gli assi xy con origine nel punto D. Per una generica sezione “s” distante x dall’origine, lo sforzo di taglio risulta:
T(x) = – 20 – qx = – 20 – 16x
(variazione lineare)
Per x = 0 (punto D)
T = – 20 kN
Per x = 2 m (punto B)
T = – 20 – 16 · 2 ≅ – 52 kN = – RB
Con i valori precedentemente indicati si può tracciare il diagramma del taglio
E’ opportuno sottolineare che nelle sezioni corrispondenti ai vincoli di estremità (punti
A e B) l’intensità dello sforzo normale risulta pari al modulo della componente di reazione diretta secondo la direzione parallela all’asse della trave, mentre l’intensità dello
88
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
sforzo di taglio è uguale al modulo della componente di reazione diretta secondo la direzione perpendicolare all’asse della trave. Questa affermazione è di validità generale
per i vincoli ubicati alle estremità delle travi.
Si osserva che il punto in cui si annulla lo sforzo di taglio corrisponde alla mezzeria della proiezione orizzontale della struttura esaminata.
Si noti che l’area del diagramma T corrispondente alla parte della trave che precede la
sezione E (mezzeria della proiezione orizzontale della struttura) risulta uguale alla
somma delle aree delle due porzioni del diagramma T che seguono la sezione E.
45.24
Area diagramma = 84.5 kNm
A
Area diagramma = 84.5 kNm
E
3.7
D
36
B
20
m
1. 4
52 kN
17.4
36
m
2m
Area diagramma fino al punto E =
Area diagramma da E a B =
45.24 ⋅ 3.736
≅ 84.5 kNm
2
17.4 ⋅ 1.436 20 + 52
+
⋅ 2 ≅ 84.5 kNm
2
2
L’area pari a 84.5 kNm rappresenta il valore massimo del momento flettente ed è uguale
a quello che si ottiene per una trave ad asse rettilineo orizzontale di luce pari a 6.5 m
soggetta a carico ripartito q = 16 kN/m: M max
q ⋅ l 2 16 ⋅ 6.52
=
=
= 84.5 kNm.
8
8
• Momento Flettente
Considerando le componenti trasversali all’asse x’
89
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Componenti trasversali che
Componenti trasversali che
agiscono sul tratto AD
agiscono sul tratto DB
y’
p=
A
1 2.
11
RAy’ =
45.24
kN
/m
y
q = 16 kN/m
s
5. 1
72 kNm
72
17.40
m
B
D
D
72 kNm
s
x’
20 kN
x
RB =
52 kN
2m
in una generica sezione “s” del tratto AD, l’espressione del momento flettente è:
M(x’) = 45.24x’ – p
x'2
x'2
= 45.24x’ – 12.11
(andamento di 2° grado, paraboli2
2
co)
Per x’ = 0 (punto A)
M=0
Il momento flettente massimo si manifesta nella sezione E di ascissa x ' ≅ 3.736, in cui si
annulla lo sforzo di taglio.
Mmax = M(x’=3.736) = 45.24 · 3.736 – 12.11
Per x’ = 5.172 (punto D)
3.7362
≅ 84.5 kNm
2
M = 45.24 · 5.172 – 12.11
5.172 2
≅ 72 kNm
2
Tutti i valori di M sono positivi, le fibre inferiori risultano sempre tese mentre quelle
superiori sono compresse.
La concavità e la pendenza del diagramma del momento flettente possono essere desunte dall’andamento del diagramma del taglio. Tra le sezioni A ed E il taglio risulta positivo quindi la pendenza del diagramma del momento flettente dovrà essere negativa, inoltre il taglio è decrescente perciò la pendenza diminuisce fino ad annullarsi nella sezione E ove si verifica il momento massimo. A partire dalla sezione E il taglio è negati-
90
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
vo e crescente (in valore assoluto) quindi il diagramma M dovrà avere pendenza positiva e crescente con x’. La concavità risulterà perciò verso l’alto.
Per il tratto DB si considerano gli assi xy con origine in D. La variazione del momento
flettente è data dalla relazione:
x2
(variazione di 2° grado, parabola)
M(x) = 72 – 20 x – 16
2
Si osservi che nell’origine D agiscono il momento 72 kN e la forza di 20 kN che corrispondono alle azioni trasmesse dal tratto AD al tratto DB.
Per x = 0 (punto D)
M = 72 kNm
Per x = 1 m (mezzeria tratto DB)
M = 72 – 20 – 16/2 = 44 kNm
Per x = 2 m (punto B)
M = 72 – 20 · 2 – 16
22
=0
2
Nel tratto DB, essendo il taglio negativo e crescente, il diagramma M presenta sempre
pendenza positiva e crescente.
Con i dati ottenuti precedentemente si può tracciare il diagramma del momento flettente.
91
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Si osserva infine che:
-
Nella trave a ginocchio vincolata agli estremi mediante una cerniera ed un carrello,
le reazioni vincolari ed i momenti flettenti sono gli stessi di quelli corrispondenti ad
una trave orizzontale rettilinea con la medesima luce. Nel tratto obliquo della trave a
ginocchio gli sforzi di taglio risultano diversi da quelli della trave rettilinea ed inoltre appaiono sforzi normali.
-
Il segno delle caratteristiche della sollecitazione indica il tipo di deformazione indotta. L’incurvamento prodotto dal momento flettente in genere rappresenta il tipo di
deformazione più evidente che può presentare la struttura.
92
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Applicazione: Trave a ginocchio con carico ripartito uniforme
Calcolo delle reazioni vincolari e delle caratteristiche della sollecitazione - Diagrammi
Una trave a ginocchio ADB è vincolata in A con un carrello (piano di giacitura del carrello parallelo al tratto AD), e in B con una cerniera. Sulla struttura agisce un carico q
uniformemente ripartito, come indicato in figura.
q = 10 kN/m
D
B
RBx
5m
RBy
45°
A
45°
RA
5m
5m
¾ Determinazione delle reazioni vincolari
La direzione della reazione RA è ortogonale alla direzione del tratto AD, risulta quindi
inclinata di 45° rispetto all’orizzontale. Al posto di RA si possono considerare le componenti RAx e RAy.
2
RA
2
RAx =
RAy =
RAy
2
RA
2
RA
45°
RAx
Assunti per le reazioni i versi indicati in figura, le equazioni di equilibrio forniscono le
seguenti relazioni:
1)
∑F
x
=0
−
2
R A + RBx = 0
2
RBx =
93
2
RA
2
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
2)
∑F
3)
∑M
y
=0
A
=0
− q ⋅ 10 +
2
R A + RBy = 0
2
2
R A = 100 − RBy
2
− q ⋅ 10 ⋅ 5 + 10 ⋅ RBy − 5 ⋅ RBx = 0
10 ⋅ RBy − 5 ⋅ RBx = 500
Dalle equazioni 1) e 2) risulta RBx = 100 − RBy
sostituendo RBx nella 3) si ha: 10 ⋅ RBy − 5 ⋅ (100 − RBy ) = 500 da cui:
RBy =
1000
≅ 66.67 kN il verso ipotizzato è corretto, la reazione va verso l’alto (Ç)
15
Dall’equazione 2) si ottiene:
R A = 2 (100 − RBy ) = 2 (100 − 66.67) ≅ 47.14 kN,
anche in questo caso il verso ipotizzato per la reazione è corretto.
Le componenti orizzontale e verticale sono, rispettivamente:
RAx =
2
RA ≅ 33.33 kN (verso sinistra Å)
2
RAy =
2
RA ≅ 33.33 kN (verso l’alto Ç).
2
Infine, dall’equazione 1) si ottiene:
2
RA ≅ 33.33 kN (verso destra Æ)
2
RBx =
Verifica delle reazioni vincolari:
∑M
D
=0
− R A ⋅ 2 5 + RBy ⋅ 5 = 0
− 47.14 ⋅ 2 5 + 66.67 ⋅ 5 = 0
Si noti che sia RBx che il risultante dei carichi ripartiti passano per D, quindi i loro momenti rispetto a D sono nulli.
94
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Diagramma del corpo libero in equilibrio
q = 10 kN/m
B
D
RBx = 33.33 kN
RBy = 66.67 kN
A
RA= 47.14 kN
Gli assi locali delle caratteristiche della sollecitazione non sono gli stessi per i due tratti
AD e DB poiché, per definizione, devono corrispondere alle rispettive linee d’asse e alle
loro perpendicolari.
y
x’
D
D
B
x
y’
A
Per il tratto AD, il carico ripartito “q” va scomposto nelle componenti trasversale ed assiale al tratto, infatti il carico “q” è definito con riferimento alla proiezione orizzontale
mentre la linea d’asse del tratto AD è inclinata rispetto all’orizzontale. Tale carico, definito per unità di lunghezza orizzontale, può essere ricondotto all’ascissa x’ parallela
all’asse della trave e decomposto in una componente “p” ortogonale all’asse della trave
ed una componente “n” parallela all’asse, entrambe riferite all’unità di lunghezza inclinata, attraverso le seguenti relazioni:
p = p(x’) = q ⋅ cos2α
n = n(x’) = q ⋅ senα ⋅ cosα
per α = 45° si ottiene:
2
 2
 = 5 kN/m
p = 10 ⋅ 

 2 
95
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
n = 10 ⋅
2 2
⋅
= 5 kN/m
2 2
q
x’
n
p = q cos 2α
p
n = q senα cosα
5/
co
sα
α = 45°
5m
¾ Caratteristiche della sollecitazione
• Sforzo Normale
Tratto AD: Lo sforzo normale nel tratto AD si ottiene accumulando la componente assiale n a partire da A. Si noti che la reazione RA non interviene perché è perpendicolare
all’asse x’ e quindi non ha componente assiale. In una sezione generica “s” lo sforzo
normale è pari alla risultante dei carichi assiali che precedono la sezione e quindi:
N(x’) = n ⋅ x’ = 5x’
la variazione dello sforzo normale è pertanto lineare ed il suo diagramma è rappresentato da una retta.
Per x’ = 0 (punto A)
Per x’ =
2 ⋅ 5 m (punto D)
NA = 0
ND = 5 ⋅ 2 ⋅ 5 ≅ 35.355 kN
Lo sforzo normale è di trazione lungo il tratto AD.
96
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Sforzo Normale tratto AD
x’
55
.3
y’
35
n = cost = 5 kN/m
n
35.355
s
+
x’
D
5
zio
A
A
tra
2
ne
y’
Tratto DB: L’unica componente assiale che precede (a sinistra) una generica sezione
“s” è la componente orizzontale della reazione RA, che nel punto B risulta equilibrata da
RBx. Lo sforzo normale è costante lungo il tratto DB e provoca trazione pari a
N(x) = RAx = 33.33 kN
Si noti che per la valutazione dello sforzo normale N si è tenuto conto delle componenti
assiali (parallele all’asse del tratto DB) delle forze attive e reattive agenti sul tratto esaminato.
Sforzo Normale tratto DB
D
B
s
RAx = 33.33 kN
+
33.33
D
trazione
97
RBx = 33.33 kN
33.33
B
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
• Sforzo di Taglio
Per la valutazione dello sforzo di taglio si considerano le componenti trasversali (per-
pendicolari all’asse della trave) delle forze attive e reattive che agiscono sul tratto esaminato.
Tratto AD: In una sezione generica “s” di ascissa x’, considerando le forze che precedono la sezione (a sinistra) lo sforzo di taglio vale:
T(x’) = RA − p ⋅ x’ = 47.14 − 5x’
questa espressione indica che il taglio varia linearmente.
Lo sforzo di taglio tende a generare uno scorrimento mutuo fra due sezioni contigue. In
questo caso la sezione che precede “s” tende a sollevarsi rispetto a quella che segue in
quanto la risultante delle forze perpendicolari all’asse in corrispondenza della sezione
“s” va verso l’alto, quindi il taglio viene considerato positivo.
Per x’ = 0 (punto A)
TA = RA = 47.14 kN
Per x’ = 5 2 (punto D)
TD = 47.14 − 5 ⋅ 2 ⋅ 5 ≅ 11.785 kN
Sforzo di Taglio tratto AD
x’
p = cost = 5 kN/m
11.785
208.33 kN
D
y’
11.785
s
+
2
47.14
5
A
RA = 47.14
L’area de diagramma del taglio nel tratto AD, che fornisce il momento flettente in D, è
1
pari a: Area diagramma = ( 47.14 + 11.785) ⋅ 5 2 ≅ 208.33 kNm
2
98
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Tratto DB: Nel punto D (origine degli assi locali) il taglio è dato dalla somma delle
componenti verticali di tutte le forze attive e reattive che precedono la sezione corrispondente al punto D:
TD = RAy − 5⋅q = 33.33 − 5⋅10 = − 16.67 kN rivolto verso il basso (È).
In una sezione generica “s”, lo sforzo di taglio vale:
T(x) = − 16.67 − q ⋅ x quindi nel tratto DB il taglio presenta andamento lineare.
Nel punto B, di ascissa x pari a 5 m, lo sforzo di taglio è pari a:
TB = − 16.67 − 5⋅5 = − 66.67 che corrisponde proprio al valore della reazione RBy.
L’area del diagramma del taglio nel tratto DB è pari a:
1
Area diagramma = ( −16.17 − 66.67) ⋅ 5 ≅ −208.33 kNm
2
E’ interessante segnalare che l’area del diagramma di T desunta per il tratto DB è uguale, a meno del segno a quella determinata per il tratto AD. Il valore di tale area, in valore assoluto, rappresenta il momento flettente nel nodo D, mentre la somma delle due aree rappresenta il momento nel punto B, ed è pari a zero.
Sforzo di Taglio tratto DB
q = cost = 10 kN/m
208.33
D
B
x
s
16.67
D
16.67
RBy = 66.67 kN
99
B
-
66.67
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
• Momento Flettente
Nel caso in esame, per la valutazione del momento flettente si considerano soltanto le
componenti trasversali (normali all’asse del tratto) poiché le componenti assiali passano
per il baricentro delle sezioni (braccio nullo) e quindi non producono momenti.
Come per le altre caratteristiche della sollecitazione, il diagramma dei momenti flettenti
è tracciato utilizzando come retta di riferimento la linea d’asse della trave. Le ordinate
(valori del momento) vengono disegnate dalla parte del bordo teso.
Tratto AD: Il momento del carico ripartito rispetto al baricentro di una sezione “s” di
ascissa x’ si ottiene moltiplicando il carico risultante px’ per la sua distanza da “s”, che
vale
1
x’. In una generica sezione “s” del tratto AD, il momento flettente risulta pari a:
2
1
x' 2
x’ = RA ⋅ x'’ − p
2
2
M(x’) = RA ⋅ x’ − p x’ ⋅
(andamento di 2° grado)
La funzione momento cresce di un grado rispetto al taglio e l’andamento è di tipo parabolico.
Per x’ = 0
(punto A)
MA = 0
5 2
2
(punto E)
ME = 166.665 − 31.25 ≅ 135.42 kNm
Per x’ = 5 2
(punto D)
MD = 333.33 − 125 ≅ 208.33 kNm
Per x’ =
Momento Flettente tratto AD
x’
p = cost = 5 kN/m
208.33 kNm
D
11.785 kN
208.33
E
E
+
2
y’
5/
2
x
s
2
x
5/
2
RA=47.14 kN
135.42
A
+
100
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Per quanto riguarda la concavità da attribuire alla parabola, si osservi che essendo il taglio decrescente con l’ascissa x’, la parabola dovrà avere pendenza (inclinazione della
tangente) massima ove il taglio è massimo (punto A) e pendenza minima dove il taglio è
minimo (punto D). Inoltre, essendo il taglio sempre positivo, la pendenza del diagramma del momento flettente sarà sempre negativa.
x’
D
+
E
+
y’
A
pendenza negativa (riferita agli assi x’y’) e decrescente
Una indicazione utile per definire la concavità della parabola è fornita anche dal valore
che assume il momento flettente in mezzeria (punto E), tale valore (135.42 kNm) risulta
maggiore di quello che corrisponde ad un ipotetico andamento lineare (208.33/2=104.17
kNm), perciò la concavità è rivolta verso l’alto.
In una generica sezione, considerando la parte di trave precedente (a sinistra), il momento delle forze tende ad allungare le fibre inferiori e ad accorciare quelle superiori,
quindi il momento flettente è considerato positivo.
Tratto DB: Il momento flettente determinato nella sezione del punto D supposta appartenente al tratto AD è il medesimo che esiste nello stesso punto D considerato come appartenente al tratto DB. Infatti, al passare dal tratto AD al DB non mutano né la direzione (ortogonale al piano della rappresentazione) né il verso del vettore momento.
La funzione momento risulta:
M(x) = 208.33 − 16.67 x − q
Per x = 0
(punto D)
x2
2
(andamento di 2° grado, parabola)
MD = 208.33 kNm
Per x = 2.5 m (punto F)
MF = 208.33 − 16.67 ⋅ 2.5 − 5 ⋅ 2.52 ≅ 135.41 kNm
Per x’ = 5 m
MB = 208.33 − 16.67 ⋅ 5 − 5 ⋅ 52 ≅ 0 kNm
(punto B)
101
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Momento Flettente tratto DB
q = cost = 10 kN/m
208.33
D
B
x
D
208.33
s
16.67
F
B
0
+
RBy = 66.67 kN
+
135.41 kNm
Per quanto concerne la concavità del diagramma, si noti che essendo il taglio decrescente con l’ascissa x, il diagramma avrà pendenza minima ove il taglio è minimo (punto D)
e pendenza massima ove il taglio è massimo (punto B). Inoltre, essendo il taglio sempre
negativo, la pendenza del diagramma del momento flettente sarà sempre positiva. Quindi la concavità è rivolta verso l’alto.
y’
B
D
pendenza positiva e crescente
x’
+
E’ possibile assumere l’ascissa x* a partire dal punto B (esaminando il problema da destra a sinistra), questo rende più comoda la valutazione del momento flettente poiché
non intervengono direttamente le azioni trasmesse dal tratto AD. Il percorrere l’ascissa
da destra a sinistra non altera il risultato ma porta ad una funzione più semplice, sempre
però di secondo grado (parabola).
y*
q = 10 kN/m
D
B
x*
s
RBy = 66.67 kN
Nella sezione generica si ha
102
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
2
x*
M(x ) = RBy ⋅ x − q
2
*
*
Per x* = 0
= 66.67 x* − 5 x*2
(punto B)
MB = 0
Per x* = 2.5 m (mezzeria tratto DB) M = 66.67 ⋅ 2.5 − 5 ⋅ 2.52 ≅ 135.41 kNm
Per x* = 5 m
MD = 66.67 ⋅ 5 − 5 ⋅ 52 ≅ 208.33 kNm
(punto D)
che sono gli stessi valori ottenuti precedentemente percorrendo l’ascissa x da D verso B.
Si noti che il momento è sempre positivo perché tende ad allungare le fibre inferiori e ad
accorciare le fibre superiori.
Riepilogo diagrammi delle sollecitazioni
35.355
33.33
+
+
D
Digramma dello Sforzo Normale
N (kN)
B
trazione
A
11.785
D
B
-
+
66.67
Diagramma dello Sforzo di Taglio
T (kN)
16.67
47.14
A
103
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
D
B
Diagramma del Momento Flettente
+
M (kNm)
+
208.33
A
+
fibre superiori compresse
fibre inferiori tese
Equilibrio nodo D
16.67 kN
Σ Fx = 0
208.33 kNm
33.33 kN
Σ Fy = 0
ΣM = 0
33.33 kN
208.33 kNm
16.67 kN
104
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Applicazione: Sistema di travi articolate
Reazioni vincolari - Caratteristiche della sollecitazione - Diagrammi
q = 10 kN/m
C
M = 200 kNm
4m
2m
D
α
A
2m
α
4m
2
B
α = 45°
2
¾ Calcolo delle reazioni vincolari
Al solo fine del calcolo delle reazioni il carico ripartito può essere sostituito con il risultante F = qL = 10 kN/m · 4 m = 40 kN. Inoltre, per le reazioni si ipotizzano i versi indicati in figura.
C
F = 40 kN
M = 200 kNm
2m
2m
y
D
RAx
B
x
A
RAy
2m
RBy
2
2
2
Equazioni globali di equilibrio (relative all’intero sistema)
1) Σ Fx = 0
RAx – RBx = 0
Æ
2m
RAx = RBx
105
RBx
2m
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
2) Σ Fy = 0
Æ
RAy – 40 + RBy = 0
RAy = 40 – RBy
3) Σ MA = 0
– 40 · 2 − 200 + RBy · 8 = 0
Æ
RBy = 35 (verso l’alto Ç)
Equazione ausiliaria
4) Σ MCB = 0 (corpo BC)
− 200 − RBx · 4 + RBy · 4 = 0
Æ
RBx =
− 200 + 4 R By
4
Risoluzione
•
Sostituendo RBy = 35 nell’equazione 2) si ha:
RAy = 40 – 35 = 5 (verso l’alto Ç)
•
Sostituendo RBy = 35 nell’equazione 4) si ottiene:
RBx =
•
− 200 + 4 ⋅ 35
= − 15 (verso destra Æ)
4
Dall’equazione 1) si ricava immediatamente:
RAx = − 15 (verso sinistra Å)
Per il calcolo delle reazioni interne, si utilizzano le equazioni di equilibrio del corpo BC
RCx
C
200 kNm
RCy
2m
D
RBx = 15 kN
B
2m
RBy = 35 kN
2
2
Σ Fx = 0
− RCx +15 = 0
Σ Fy = 0
RCy + 35 = 0
Æ
Æ
RCx = 15 (verso sinistra Å)
RCy = -35 (verso il basso È)
106
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Verifica dell’equilibrio del corpo AC
RCy = 35 kN
RCx = 15 kN
F = 40 kN
C
2m
2m
RAx = 15 kN
A
RAy = 5 kN
2m
Σ Fx = 0
− 15 +15 = 0 9
Σ Fy = 0
5 − 40 + 35 = 0 9
2
Σ MA = 0 − 40 · 2 − 15 · 4 + 35 · 4 = 0 9
Riepilogo forze agenti (attive e reattive)
q = 10 kN/m
35 kN
y”
C
15 kN
x’
y’
15 kN
C
x”
15 kN
D
35 kN
A
200 kNm
B
15 kN
5 kN
35 kN
Innanzitutto, per ogni tratto si decompongono le forze agenti (attive e reattive) secondo
le direzioni parallele e normali all’asse.
Essendo α = 45°, si ha: cosα = senα ≅ 0.707
107
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
a) Decomposizione di RAx e RAy secondo le direzioni parallela e perpendicolare
all’asse del tratto AC (assi x’ e y’)
C
RAy cosα
RAx = 15
A
α RAy = 5
RAx senα
x’
x’
y’
RAy senα
α
y’
C
α
A
α
RAx cosα
RAx’ = RAy senα - RAx cosα
RAy’ = RAy cosα + RAx senα
componente parallela all’asse x’ = R Ax' = 5 sen α − 15 cos α ≅ −7.07
componente normale all’asse x’ = R Ay' = 5 cos α + 15 sen α ≅ 14.14
b) Decomposizione di RCx e RCy secondo le direzioni parallela e perpendicolare
all’asse del tratto AC (assi x’ e y’)
RCy = 35 α
RCy cosα
RCx cosα
RCy senα
C
α
A
x’
y’
x’
y’
C
RCx senα
α
RCx = 15
α
A
RCx’ = RCy senα + RCx cosα
RCy’ = RCy cosα - RCx senα
componente parallela all’asse x’ = R Cx' = 35 sen α + 15 cos α ≅ 35.36
componente normale all’asse x’ = R Cy' = 35 cos α − 15 sen α ≅ 14.14
c) Decomposizione di RCx e RCy secondo le direzioni parallela e perpendicolare
all’asse del tratto BC (assi x” e y”)
108
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
RCy cosα
α
RCx cosα
RCx senα
C
y”
α
RCx = 15 C
y”
RCy senα
RCy = 35
x”
x”
α
α
B
B
RCx” = RCy senα - RCx cosα
RCy” = - RCy cosα - RCx senα
componente parallela all’asse x” = R Cx' ' = 35 sen α − 15 cos α ≅ 14.14
componente normale all’asse x” = R Cy'' = −35 cos α − 15 sen α ≅ −35.36
d) Decomposizione di RBx e RBy secondo le direzioni parallela e perpendicolare
all’asse del tratto BC (assi x” e y”)
y”
y”
C
C
x”
x”
α
α
B
B
RBy senα
RBy = 35
α
RBy cosα
RBx cosα
RBx = 15
α
RBx senα
RBx” = - RBy senα + RBx cosα
RBy” = RBy cosα + RBx senα
componente parallela all’asse x” = R Bx' ' = −35 sen α + 15 cos α ≅ −14.14
componente normale all’asse x” = R By'' = 35 cos α + 15 sen α ≅ 35.36
e) Decomposizione del carico ripartito agente sul tratto AC (q = 10 kN/m)
componente parallela all’asse x’ = n = 10 sen α cos α = 5 kN/m
componente normale all’asse x’ = p = 10 cos 2 α = 5 kN/m
109
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
Componenti assiali delle forze agenti (attive e reattive)
35.36 kN
14.14 kN
C
n=
5
kN
/m
C
B
A
7.07 kN
14.14 kN
Componenti trasversali delle forze agenti (attive e reattive)
35.36 kN
kN
/m
C
C
200 kNm
p
=
5
14.14 kN
D
8
82
2.
5.
65
7
m
8
82
2.
A
B
35.36 kN
14.14 kN
¾ Caratteristiche della sollecitazione
• Sforzo Normale
Considerando gli assi x’y’ con origine in A, la funzione sforzo normale nel tratto AC
vale
N(x’) = 7.07 + nx’ = 7.07 + 5x’ (andamento lineare)
Per x’ = 0 (punto A)
N = 7.07 kN (trazione)
Per x’ = 2.828 (mezzeria tratto AC)
N = 7.07 + 5 · 2.828 ≅ 21.21 kN (trazione)
Per x’ = 5.657 (punto C)
N = 7.07 + 5 · 5.657 ≅ 35.36 kN (trazione)
Nel tratto CB lo sforzo normale è costante:
110
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
N = − 14.14 (compressione)
Con i valori ricavati si può tracciare il diagramma
+
C
Digramma dello Sforzo Normale N
r
mp
tra
co
zio
ne
35.36 kN
es
si o
-
ne
7.07 A
B
14.14 kN
• Sforzo di Taglio
In una generica sezione “s” del tratto AC, lo sforzo di taglio vale:
T(x’) = 14.14 – px’ = 14.14 – 5x’ (variazione lineare)
Per x’ = 0 (punto A)
T = 14.14 kN
Per x’ = 2.828 (mezzeria tratto AC)
T = 14.14 − 5 · 2.828 ≅ 0
Per x’ = 5.657 (punto C)
T = 14.14 – 5 · 5.657 ≅ − 14.14 kN
Lo sforzo di taglio si annulla in mezzeria.
Nel tratto CB lo sforzo di taglio è costante:
T = − 35.36 kN
Con i valori trovati si può tracciare il diagramma del taglio
C
-
14.14 kN
Digramma dello Sforzo di Taglio T
+
14.14 kN
A
B
35.36 kN
111
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
• Momento Flettente
In una generica sezione “s” del tratto AC, l’espressione del momento flettente è:
M(x’) = 14.14x’ – p
x'2
x'2
= 14.14x’ – 5
(andamento parabolico)
2
2
Per x’ = 0 (punto A)
M=0
Nella sezione in cui si annulla il taglio (mezzeria) si ha il momento flettente massimo:
Mmax = M(x’=2.828) = 14.14 · 2.828 – 5
Per x’ = 5.657 (punto C)
2.8282
≅ 20 kNm
2
M = 14.14 · 5.657 – 5
5.657 2
≅0
2
Si osserva che nel punto C c’è una cerniera, pertanto il momento deve risultare nullo.
Il momento flettente è nullo nel punto A e nel punto C, nel tratto compreso tra i due estremi è positivo con un massimo in mezzeria. Le fibre inferiori risultano sempre tese
mentre quelle superiori sono compresse.
La concavità e la pendenza del diagramma del momento flettente possono essere desunte dall’andamento del diagramma del taglio. Tra la sezione A e quella di mezzeria il taglio è positivo quindi la pendenza del diagramma del momento flettente dovrà essere
negativa, inoltre il taglio è decrescente perciò la pendenza del diagramma del momento
diminuisce fino ad annullarsi nella sezione di mezzeria. A partire dalla mezzeria il taglio
è negativo e crescente (in valore assoluto) quindi il diagramma M dovrà avere pendenza
positiva e crescente con x’. La concavità risulterà perciò verso l’alto.
Data la presenza del momento applicato nel punto D, per il calcolo del momento flettente il tratto CB si considera diviso in due tratti: 1) tratto CD con assi x”y” e origine in C;
2) tratto DB con assi x”y” e origine in D.
Nel tratto CD il momento è dato dalla seguente espressione:
M(x”) = – 35.36x” (andamento lineare)
Per x” = 0 (punto C)
M = 0 (cerniera)
Per x” = 2.828 m (punto D)
M = – 35.36 · 2.828 = − 100 kNm
Per il tratto DB, il momento risultante nella sezione iniziale (punto D) è pari al momento in D precedentemente trovato (−100) a cui va aggiunto in momento applicato (200,
positivo perché tende le fibre inferiori). L’espressione del momento sarà:
112
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
M(x”) = − 100 + 200 – 35.36x” = 100 – 35.36x” (andamento lineare)
Per x” = 0 (punto D)
M = 100 kNm
Per x” = 2.828 m (punto B)
M = 100 – 35.36 · 2.828 = 0
Con i dati ottenuti precedentemente si può tracciare il diagramma del momento flettente.
C
-
+
100
A
Digramma del Momento Flettente M
20 kNm
100 kNm
+
B
+
200 kNm
113
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
1.5. Applicabilità dell’ipotesi di corpo rigido nella determinazione
delle caratteristiche della sollecitazione
Usualmente le caratteristiche della sollecitazione si determinano considerando la trave
indeformata (rigida), cioè senza tener conto degli spostamenti che subiscono i punti di
applicazione delle forze esterne in seguito alla deformazione. In altre parole, per il calcolo delle caratteristiche della sollecitazione si accetta la validità dell’ipotesi di corpo
rigido. L’analisi strutturale condotta sul sistema indeformato usualmente si denomina
Teoria del Primo Ordine.
Tuttavia, in certi casi è necessario tenere conto degli spostamenti poiché possono avere
significativa influenza sui valori delle caratteristiche della sollecitazione (specialmente
sul momento flettente). Quando l’analisi strutturale è realizzata considerando gli spostamenti (struttura deformata) si denomina Teoria del Secondo Ordine. Un caso illustrativo delle situazioni in cui gli spostamenti non sono più trascurabili corrisponde alla
presso flessione nei pilastri snelli.
Si consideri la trave verticale incastrata (molto lunga rispetto alle dimensioni della sezione e perciò significativamente flessibile) soggetta ai carichi esterni concentrati H e P.
P
P
H
Momenti
addizionali causati
dalla deformazione
H
h/2
δ
M = H x h/ 2
h/2
-
M = H xh
Trave indeformata
Teoria del Primo Ordine
M = H x h/ 2
+P xδ
-
f
M = H xh+ P xf
Trave deformata
Teoria del Secondo Ordine
La trave, prevalentemente per effetto della forza orizzontale H, tende ad inflettersi come
indicato in figura. In tale situazione, a causa della deformazione, le distanze della retta
d’azione di P dai baricentri delle varie sezioni non sono più nulle e appaiono eccentrici114
Corso di Statica e Teoria delle Strutture. Prof. Luis Decanini. Caratteristiche della sollecitazione
tà crescenti dall’alto verso il basso. A metà altezza tale distanza vale δ, mentre nella sezione d’incastro l’eccentricità è uguale ad f. In questa situazione è necessario valutare il
momento flettente considerando la trave deformata. Nella sezione d’incastro l’analisi
sulla trave indeformata fornisce un momento flettente pari a H · h, mentre considerando
la deformazione il momento flettente vale H · h + P · f, che può risultare significativamente maggiore di quello calcolato sulla trave indeformata.
Ad ogni modo giova segnalare che, nella maggior parte delle applicazioni correnti, per
l’analisi delle strutture è sufficiente il calcolo delle caratteristiche della sollecitazione
considerando la struttura indeformata, procedura che peraltro può essere vista come fase
iniziale dell’analisi sulle strutture deformate.
Alcuni esempi di strutture o di elementi strutturali
in cui si può esaminare il sistema indeformato
Ossatura
edificio in c.a.
Portale padiglione
industriale
115
Arco a sesto acuto
in muratura