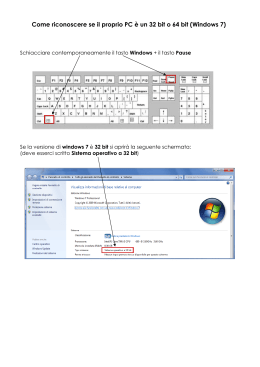
Ottimizzazione Openssl su Itanium 2/OpenVMS
Riccardo Giacomelli
8 febbraio 2005
2
Indice
I
Architettura Itanium 2
0.1
0.2
0.3
II
7
Introduzione Itanium 2 processore RISC
0.1.1 EPIC . . . . . . . . . . . . . . .
Architettura generale . . . . . . . . . . .
0.2.1 Execution model . . . . . . . . .
0.2.2 Unitá funzionali e issue rules . .
0.2.3 Bundles e Dipersal Rules . . . .
0.2.4 Pipeline . . . . . . . . . . . . . .
0.2.5 Memory Hierarchy . . . . . . . .
Meccanismi innovativi di Itanium . . . .
0.3.1 Registri . . . . . . . . . . . . . .
0.3.2 Register Stack . . . . . . . . . .
0.3.3 Software pipeline . . . . . . . . .
0.3.4 Speculation and Predication . . .
o
.
.
.
.
.
.
.
.
.
.
.
.
CISC?
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Assembler Itanium
9
9
10
11
11
12
15
15
15
15
16
18
18
21
1 Descrizione dell’assembler
1.1 Formato delle istruzioni
1.2 Registri . . . . . . . . .
1.3 Procedure . . . . . . . .
1.4 Explicit Bundle . . . . .
Itanium
. . . . . .
. . . . . .
. . . . . .
. . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
23
23
23
24
24
2 istruzioni principali
2.1 Add . . . . . . .
2.2 Alloc . . . . . . .
2.3 And . . . . . . .
2.4 Cmp-Cmp4 . . .
2.5 Dep . . . . . . .
2.6 Extr . . . . . . .
2.7 Ld . . . . . . . .
2.8 Nop . . . . . . .
2.9 Mix-Mux . . . .
2.10 Shl . . . . . . . .
2.11 Shr . . . . . . . .
2.12 Shrp . . . . . . .
2.13 Xor . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
27
27
27
28
28
28
28
29
29
29
30
30
30
31
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
INDICE
III
Ottimizzazione degli Algortimi
33
2.14 Introduzione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
3 Linee generali
3.1 Ottimizzazione generale del codice . . . . . . . .
3.1.1 Load-Store . . . . . . . . . . . . . . . . .
3.1.2 Cicli e loop unrolling . . . . . . . . . . . .
3.2 Ottimizzazione dell’assembler . . . . . . . . . . .
3.3 Fasi di Ottimizzazione degli Algoritmi . . . . . .
3.4 Operazioni presenti in tutti gli algoritmi . . . . .
3.4.1 Uso di Costanti . . . . . . . . . . . . . . .
3.4.2 Selezione di bits da registro . . . . . . . .
3.4.3 Look up in tabella . . . . . . . . . . . . .
3.4.4 Uso delle load . . . . . . . . . . . . . . . .
3.4.5 Xor tra una serie di valori . . . . . . . . .
3.4.6 Htonl Ntohl . . . . . . . . . . . . . . . . .
3.4.7 Uso dei bundles per le istrzioni assembler
3.5 Regole Generali per Itanium . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
37
37
37
38
39
39
40
40
40
41
41
42
42
43
44
4 DES
4.1 Caratteristiche Principali . . . . . . . . . . . .
4.1.1 Permutazioni . . . . . . . . . . . . . . .
4.1.2 32 bit-64 bit . . . . . . . . . . . . . . .
4.1.3 Table look-up . . . . . . . . . . . . . . .
4.2 Ottimzzazione DES in Dettaglio . . . . . . . .
4.2.1 Initial Permutation e Final Permutation
4.2.2 16 Rounds . . . . . . . . . . . . . . . . .
4.2.3 Ottimizzazione in Itanium . . . . . . . .
4.3 Risultati . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
45
45
45
46
47
48
48
50
51
51
5 RC5-32/12/16
5.1 Caratteristiche Principali . . . . . . . . .
5.1.1 Rotate variabili . . . . . . . . . . .
5.1.2 Add modulo 232 . . . . . . . . . .
5.2 Ottimzzazione RC5-32/12/16 in Dettaglio
5.2.1 RC5-32/12/16 single round . . . .
5.2.2 Ottimizzazioni in Itannium . . . .
5.3 Risultati . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
53
53
53
53
54
54
55
56
6 SHA-1
6.1 Caratteristiche Principali . . . . . . . . .
6.2 Descrizione dell’algoritmo e ottimizzazione
6.2.1 Descrizione dei round . . . . . . .
6.2.2 Espansione delle word . . . . . . .
6.3 Ottimizzazione SHA-1 nel dettaglio . . . .
6.3.1 Singolo Round . . . . . . . . . . .
6.3.2 Espansione delle word . . . . . . .
6.3.3 Ottimizzazione in Itanium . . . . .
6.4 Risultati . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
57
57
58
58
58
59
59
59
59
60
INDICE
5
7 AES (Rijndael)
7.1 Caratteristiche Principali . . . . . .
7.1.1 Scelta dell’implementazione .
7.2 Ottimizzazione AES nel dettaglio . .
7.2.1 Ottimizzazione dell’algoritmo
7.3 Ottimizzazione In Itanium . . . . . .
7.4 Risultati . . . . . . . . . . . . . . . .
IV
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Appendix
65
65
65
66
69
70
71
73
8 Help Itanium/OpenVMS
8.1 Assembler Itanium . . .
8.2 Compilare il codice . . .
8.3 Linking . . . . . . . . .
8.4 Debugger . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
75
75
75
76
76
9 Summary
9.1 DES . . . . . . . . .
9.1.1 DES Results
9.2 RC5-32/12/16 . . . .
9.3 AES . . . . . . . . .
9.4 SHA-1 . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
79
79
79
80
80
82
.
.
.
.
.
.
.
.
.
.
6
INDICE
Parte I
Architettura Itanium 2
7
0.1. INTRODUZIONE ITANIUM 2 PROCESSORE RISC O CISC?
0.1
9
Introduzione Itanium 2 processore RISC o
CISC?
In Internet, in molti articoli riguardanti Itanium, questo processore viene definito a volte un RISC a volte un CISC; entrambe le definizioni hanno un qualcosa
di vero. Si definiscono RISC, ovvero Reduct Set of Istruction Computing quei
processori che possiedono un ridotto set di istruzioni assembler e non hanno
nel loro set istruzioni complicate, come ad esempio le operazioni sulle stringhe dell’8086. L’idea su cui si basano i processori RISC é quella di risolvere i
problemi complicati e lunghi, invece che con una sola istruzione, in piú passi,
suddividendo l’operazione complessa in una serie di piú istruzioni semplici. Disponendo solo di istruzioni semplici, i RISC sono in grado di eseguire molte piú
istruzioni al secondo rispetto ai CISC. I processori CISC sono quelli che hanno
implementate un vasto numero di istruzioni e dispongono di istruzioni complicate quali, ad esempio, l’istruzione di rotate di un registro o le operazioni su
stringhe. Il processore Itanium sicuramente un processore RISC perché dispone
di operazioni semplici che durano un colpo di clock. Un esempio concreto é dato
dal fatto che l’operazione add esiste solo con operandi contenuti in registri , e
quindi per fare add di un operando in memoria bisogna prima caricarlo in registro con una operazione di load. Oppure, altro esempio, non ha supporto per
rotate variabile di registro. Allo stesso tempo possiede anche istruzioni complicate: prendiamo ad esempio la extr che permette di selezionare un sottoinsieme
di bit da un registro, operazione che di solito era fatta con shift + and con
maschera. Basti pensare che su Itanium 2 sono implemetate oltre 150 istruzioni, ognuna della quali ha delle varianti. Per quanto riguarda la compatibilitá
con le versioni assembler precedenti si adottano delle soluzioni quali l’utilizzo
di pipeline separate per eseguire codice in assembler non Itanium. Oppure si
adotta una memoria di microcodice in cui per ogni istruzione complicata c’é la
serie di istruzioni semplici corrispondente. Quando si deve eseguire una istruzione complessa si effettua un jump nella memoria di microcodice e si eseguono
le istruzioni semplici corrispondenti. Concludendo, nella sua struttura Itanium
un processore RISC superscalare in quanto riesce a compiere ben 6 istruzioni
per colpo di clock, ma avendo al tempo stesso anche caratteristiche CISC. In
realtá Itanium va oltre i processori RISC e CISC. Il termine esatto per definire
l’architettura Itanium EPIC.
0.1.1
EPIC
Una caratteristica di Itanium che il processore esegue le operazioni nell’ordine in cui gli vengono fornite dal compilatore. Non ha nessun meccanismo di
riordino delle istruzioni, non ha alcun meccanismo di ottimizzazione del codice
al momento dell’esecuzione. In processori come il Pentium esisteva un pool di
istruzioni di cui il processore aveva eseguito il fetch; poteva poi decidere di farne
avanzare alcune mentre altre erano in stallo, oppure era in grado di cambiare
l’ordine di esecuzione delle istruzioni. Questo meccanismo, se da un lato era
utile per cercare di eseguire in modo piú veloce possibile il codice, dall’altro
presupponeva l’esistenza di una serie di processi per controllare che l’esecuzione del codice fosse ancora corretta, verificava che tutte le dipendenze fossero
state rispettate ecc. L’architettura risultante diventava molto complicata. In
10
Itanium, invece, la strategia é cambiata: il processore esegue in ordine tutte
le istruzioni senza cercare di modificarne la sequenza. A questo punto é chiara limportanza fondamentale del compilatore, poiché il codice compilato verrá
eseguito cosı́ com’é stato compilato. La scelta di Itanium é quella di dare pieno
controllo del processore al programmatore. Le istruzioni sono molto accurate,
permettono addirittura di controllare la cache. Tuttavia, proprio per il fatto
che si ha pieno controllo sul processore e le istruzioni sono ricche di dettagli,
la programmazione in assembler Itanium e la realizzazione di compilatori per
Itanium risultano complicate. EPIC significa Explicit Parallel Instruction Computing. Questo paradigma ha portato a una rivoluzione, ovvero a seguire una
linea di progetto che lascia solo le procedure semplici ed essenziali nel core, mentre quelle piú complicate vengono demandate ad altri, ovvero al compilatore. Il
compilatore prepara il codice, mentre il processore, con un’espressione trovata
sul sito Intel, will rock it, ovvero lo eseguirá molto velocemente. Al tempo stesso
in Itanium sono implementati nuovi meccanismi che complicano l’architettura .
Essi saranno presentati nella sezione seguente.
0.2
Architettura generale
La grande capacitá di eseguire istruzioni permette a Itanium di sfruttare al
massimo il parallelismo esistente nel codice, a condizione che venga scritto e
compilato in modo adeguato. (Piú avanti verrá spiegato meglio come). Le
caratteristiche piú importanti di Itanium sono:
1. Architettura interamente a 64 bit
2. Vasto set di istruzioni
3. Gran numero di registri
4. Struttura di accesso alla memoria ottimizzata
5. gran numero di unitfunzionali in grado di eseguire 6 istruzioni per clock
6. Register Stack-meccanismi innovativi per gestire i registri e i passaggi di
parametri a funzione
7. Software pipeline-meccanismi innovativi per gestire i loop
8. Cache instructions-istruzioni per controllare direttamente la cache
9. Speculation and Predication-meccanismi di speculazione e predicati innovativi
Itanium dispone di un’architettura interamente a 64 bit; sia i registri che i bus
che la pipeline e le unitá funzionali hanno tutte parallelismo 64 bit. La vera
innovazione consiste nell’avere le unitá funzionali e i registri a 64 bit, perché
giá altri processori come il pentium disponevano di un bus a 64 bit per migliorare il bandwidth verso l’esterno del processore, ma non disponevano di unitá
funzionali a 64 bit.
0.2. ARCHITETTURA GENERALE
0.2.1
11
Execution model
Itanium puó eseguire fino a 6 istruzioni per colpo di clock. Il processore esegue
le istruzioni tre a tre. Un gruppo di istruzioni viene denominato Bundle. Il
processore esegue quindi due Bundle per colpo di clock. Quando il processore
riesce ad eseguire 2 Boundle in un colpo di clock si verifica una situazione di
dual issue, ma non sempre riesce ad eseguirne due. In questo caso c’é uno
split issue, ovvero i due bundle vengono eseguiti in 2 colpi di clock successivi.
In definitiva il processore esegue o 3 o 6 istruzioni per clock. Questo importante
perché se anche solo una delle 3 istruzioni nel secondo Bundle non puó essere
eseguita per uno dei motivi citati dopo, tutte e tre le istruzioni verranno eseguite
al clock successivo. I motivi per cui ci puó essere uno split issue sono:
1. uno stop esplicito é stato incontrato. Lo stop é rappresentato con ;;
2. non ci sono abbastanza risorse per eseguire tutte le istruzioni
3. Le istruzioni non sono state poste nel Bundle seguendo le regole di dispersal Itanium
Le regole di dispersal definiscono in che modo le istruzioni debbano essere posizionate nel bundle. Esse saranno spiegate nelle subsection successive. Ritornando a processori come il Pentium, questi avevano un’architettura piú complicata
anche perché dovevano occuparsi di controllare i cosidetti hazards, ovvero le situazioni in cui un registro é scritto con un nuovo valore prima che il precedente
valore potesse essere letto (WAR-Write after read). Oppure il registro viene
letto prima che il valore da leggere sia stato scritto (RAW-Read after write).
Un esempio su tutti é dato dall’istruzione che legge un registro pensando di
trovare il risultato di un’istruzione precedente, ma la precedente non era ancora
terminata. Oppure, altro esempio, dato da hazards (WAW-write after write),
cioé quando esistono 2 scritture consecutive sullo stesso registro. Come é stato
risolto in Itanium tutto questo? In veritá Itanium non se occupa minimamente: sará il compilatore ad inserire tra le due istruzioni in questione uno stop
implicito in modo da rispettare la dipendenza. Se il compilatore non inserisce
nessuno stop e si verificano degli hazard il processore, come letteralmente scritto
nei manuali intel, si comporterá in modo non deterministico e il risultato non
sará prevedibile.
0.2.2
Unitá funzionali e issue rules
Itanium 2 dispone di 6 unitá ALU. Queste vengono usate per eseguire le operazioni aritmetiche, compares, multimedia istruction ecc. Dispone di 4 porte
verso la cache per l’accesso alla memoria, due per le store, e due per le load.
Questo permette di eseguire 2 load e 2 store per colpo di clock. Possiede 2
unitá Integer(I0, I1), e una unitá shift per operazioni quali lo shift right,shift
left, ecc. In totale ha 11 porte a cui le istruzioni vengono mandate per essere
eseguite:M0, M1, M2, M3, I0, I1, F0, F1, B0, B1 e B2. Le M0-M3 sono le
porte per la memoria, ma non sono tutte uguali: M0 e M1 sono le porte per le
load, M2 e M3 sono le porte per le store. Inoltre le porte M non vengono solo
usate per gli accessi in memoria, ma anche per eseguire operazioni di tipo ALU
tipo add, and ecc. Lidea é che poiché le porte di memoria dovevano contenere
un’unitá per calcolare l’indirizzo e quindi in grado di svolgere calcoli, quando
12
Instruction Type
A1-A5
A6-A8
A
I
I5
I7
I10
I11, I12
I29
M1
M4, M5
M34
Istrutions
add, shladd
cmp, cmp4
and
xor, or
shr, shr. u
shl, shl. u
shrp
extr, extr. u, Dep
sxt, zxt, czx
ld4, ld8. .
st4st8. .
alloc
Description
add, parallel add
compare e compare 4 bytes
and logico
xor, or logico
shift right
shift left
shift right pair usato per rotate fissi
extract, Deposit
signe extended, zero extended
Integer load
Integer store
allocate frame on reg stack
M0
Y
Y
Y
Y
M1
Y
Y
Y
Y
Y
Y
M2
Y
Y
Y
Y
Y
Y
Tabella 1: principali istruzioni e porte sulle quali possono essere eseguite
queste porte non venivano usate per l’accesso in memoria potevano essere usate
per eseguire altre istruzioni. Di conseguenza, nelle porte M sono state inserite
delle vere e proprie ALU in grado di calcolare gli indirizzi di memoria quando
necessario, ma anche di eseguire operazioni aritmetiche all’occorrenza. Le porte I0 e I1 sono le porte Integer; esse eseguono operazioni quali gli shift o gli
xor, oppure istruzioni complicate quali la mix o l’extr. Un limite di Itanium é
costituito proprio da queste 2 porte. Nell’ottimizzazione degli algoritmi la maggior parte delle istruzioni era di tipo integer; Itanium, pur avendo tutte queste
unitá funzionali, puó eseguire solo 2 istruzioni Integer per colpo di clok, e per le
istruzioni piú complicate come l’extr anche solo una per clock. Le porte F0, F1
sono le Floating point, Le porte B0, B1, B2 sono le porte in cui sono eseguite le
operazioni di branch. La tabella 1 riporta le principali istruzioni e le porte su
cui possono essere eseguite. Il type delle istruzioni definisce se sono istruzioni di
tipo ALU, Integer o Memory. All’interno di questi gruppi vi sono sottoinsiemi,
per esempio A2, A4, ma le sottodivisioni non sono importanti. Quello che é importante é sapere quali istruzioni appartengono a quale gruppo, e da che unitá
funzionale possono essere eseguite. Come si vede dalla tabella 1 le istruzioni
ALU possono essere eseguite da qualunque unitá M o I, le istruzioni Integer,
sono piú limitate, per esempio la extr puó essere solo eseguita dell’unitá I0.
0.2.3
Bundles e Dipersal Rules
Le Dipersal Rules sono le regole che il processore usa per eseguire le istruzioni.
Sono molto importanti perché se non vengono rispettate, si avrá uno split
issue. Come abbiamo detto prima le istruzioni sono raggruppate in bundles
ognuno di tre istruzioni. Ciascuna delle tre posizioni all’interno del bundle é
chiamata slot. Ogni bundle ha 3 slot. La posizione in cui un’istruzione é posta
determina l’unitá funzionale da cui sará eseguita. c’é un mappaggio preciso
tra la posizione delle istruzioni e l’unitá funzionale a cui sará anno assegnate.
Questo mappaggio é chiamato dipersal. Essistono molti tipi di Bundles, per
esempio MMI, MMF, MII. Le lettere M stanno sempre per memory, A ALU, I
Integer, F floating point, B branch. Un Bundle del tipo MMI significa che ha
2 istruzioni memory e una integer. L’ordine in cui sono specificate le istruzioni
M3
Y
Y
Y
Y
Y
I0
Y
Y
Y
Y
Y
Y
Y
Y
Y
I1
Y
Y
Y
Y
Y
Y
Y
0.2. ARCHITETTURA GENERALE
MII
MLI
MMI
MFI
MMF
MIB
MBB
BBB
MMB
MFB
MMI
Y
Y
Y
Y
Y
Y
MLI
Y
Y
13
Y
Y
Y
Y
Y
MMI
Y
Y
Y
Y
Y
Y
MFI
Y
Y
Y
Y
Y
Y
MMF
Y
Y
Y
Y
Y
Y
MIB
Y
Y
Y
Y
Y
Y
MBB
Y
Y
Y
Y
Y
Y
BBB
Y
Y
Y
Y
Y
Y
MMB
Y
Y
Y
Y
Y
Y
MFB
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Tabella 2: tipi di Bundle che possono andare in dual issue
non é casuale ma preciso: prima devono essere scritte le 2 istruzioni memory, poi
l’istruzione integer. Scrivendo il codice assembler i Bundle vengono dichiarati
con 2 parentesi graffe e il tipo del bundle scritto all’inizio. Per esempio:
{. mmi
ld4 r32=[r32]
ld4[ r33=[r33]
shr r35=r35, 2
}
Un Bundle di questo tipo é un memory-memory-integer; si puó notare che l’istruzione integer occupa proprio il terzo slot nel bundle. Le dispersal rules sono
molte. Le principali per le operazioni ALU e Integer sono:
• l’istruzione nel primo slot I dei due Bundles sará eseguita da I0, La seconda
da I1.
• Se la seconda istruzione I puó essere eseguita solo da I0 ci sará uno stop
implicito e l’istruzione sará eseguita nel colpo di clock seguente
• Gli slot I non contengono solo istruzioni I ma possono contenere anche
istruzioni di tipo ALU. Se 2 istruzioni di tipo I sono giá state assegnate
alle due unitá funzionali I0 e I1, e un ulteriore slot I contiene unistruzione
ALU, questa verrassegnata ad una unitá M libera. E’ il caso dei Bundles
MMI-MMI.
Un esempio della prima regola questo:
{. mmi
ld4 r32=[r32]
ld4[ r33=[r33]
shr r35=r35, 2
}
{. mmi
ld4 r32=[r32]
ld4[ r33=[r33]
xor r35=r35, 2
};;
14
Come detto nella regola citata prima, l’istruzione shr che é la prima istruzione Integer verrá assegnata all’unitá I0, l’istruzione xor che la seconda istruzione
Integer verrá assegnata a I1. E’ importante capire che, se nei 2 bundle c’é un’istruzione tipo extr eseguibile solo da I0, questa deve essere posta nel primo slot
I, altrimenti si avrá uno split issue. esempio:
{. mmi
ld4 r32=[r32]
ld4[ r33=[r33]
shr r35=r35, 2
}
{. mmi
ld4 r32=[r32]
ld4[ r33=[r33]
extr r35=r35, 2
};;
In questo esempio lo slot I0 occupato dall’istruzione shr; l’istruzione integer
successiva cioé extr non puó essere eseguita, e c’é un split issue. Se il codice
fosse scritto nel modo seguente:
{. mmi
ld4 r32=[r32]
ld4[ r33=[r33]
extr r35=r35, 2
}
{. mmi
ld4 r32=[r32]
ld4[ r33=[r33]
shr r35=r35, 2
};;
sarebbero eseguite tutte e sei le istruzioni in un colpo di clock. La terza regola
diceva che se in uno slot integer c’é un’istruzione ALU, e le 2 unitá I0 e I1 sono
gioccupate l’istruzione assegnata ad una unitá M. esempio:
{. mii
ld4 r32=[r32]
extr r35=r35, 2
shr r35=r35, 2
}
{. mmi
ld4 r32=[r32]
st4 [r40]=r40
and r50=r50. r51
};;
le due istruzioni integer shr e extr sono assegnate alle unitá integer. Lo slot
integer del secondo bundle non puó essere assegnato ad una unitá integer, ma
siccome contiene una istruzione ALU verrá assegnata ad una unitá M. La tabella
2 indica quali tipi di bundle possono essere eseguiti insieme in un solo colpo di
clock. Non é sufficiente seguire la tebella 2 affinché si abbia dual issue, poiché
0.3. MECCANISMI INNOVATIVI DI ITANIUM
15
é sempre necessario seguire le regole di dispersal. Se non vengono rispettate ci
sará split issue anche se si sono usati 2 bundle che nella tabella 2 sembravano
poter essere eseguiti in dual issue. Per approfondimenti sulle altre regole di
dispersal consultare [1, capitolo 1.1] La regola generale quella di porre prima
nel bundle le istruzioni con piú limitazioni.
0.2.4
Pipeline
La pipeline Itanium 2 é molto lunga, ha 8 stage. Una pipeline lunga serve
soprattutto per migliorare il throughput di istruzioni per colpo di clock. Le
varie stage della pipeline non sono state approfondite perché non sono essenziali
per la comprensione dell’ottimizzazione su Itanium.
0.2.5
Memory Hierarchy
Il processore Itanium ha una cache L1-D di primo livello per i dati, una cache
L1-I per le istruzioni, una cache L2 di secondo livello unificata e una cache di
terzo livello. Il TLB(Translation lookaside buffer) per convertire gli indirizza
da cercare full associative, non verrá approfondito qui. La cosa piú importante
sono le dimensioni e le latenze della cache. La cache L1 ha dimensione 16Kbytes,
set associative a 4 vie, e una linea di cahe lunga 32 byte. La cache L2 ha
dimensione 96Kbytes, 6 way set associative e una linea di 64 bytes. La cache L3
sul processore esaminato ha dimensione 3 Mbytes. La latenza di primo livello
lavora alla velocitá del processore; per accedervi basta un colpo di clock, quindi
la latenza per accedere alla cache L1 é un colpo di clock. Per accedere alla cache
L2 la latenza di 6 colpi di clock per gli interi 9 per i floating point. La latenza
per L3 di 21 colpi di clock per gli interi e 24 per i floating point. Se c’é un
miss in L1 si controllerin L2 e se c’é ancora miss si controllerá in L3, quindi le
latenze per accedere a L3 vanno sommate. Il bus esterno dalla cache L3 alla
memoria ha una bandwidth di 2.1 Gb/secondo. Tra L3 e L2, invece, si possono
trasmettere 16 bytes/clock. Tra L2 e L1 si possono trasmettere 32 bytes/clock,
e tra L1 ed il register file si possono caricare 2 x 8 bytes/clock. Il processore
dispone di 4 porte (2 per le load e 2 per le store), quindi possono essere eseguite
al massimo 2 load di 8 bytes ciascuna e 2 store di 8 bytes ciascuna.
0.3
0.3.1
Meccanismi innovativi di Itanium
Registri
Itanium dispone di un ricco set di registri: i registri utilizzabili sono molti, come
si vede dalla figura 1. Gli Integer registers sono registri general purpose a 64 bit
e vengono utilizzati comunemente per contenere dati, indirizzi ecc. I Predicate
registers sono usati per i predicati che sono un meccanismo per velocizzare le
condizioni presenti nel codice, tipo if-else. I Branch Registers sono registri per
contenere gli indirizzi dei salti e vengono usati per velocizzare i salti presenti
nel codice. In realtá vi é un’ulteriore suddivisione nei registri General purpose
R1-R128:
• R0:sempre uguale a zero
• R1:GP(Global Data Pointer)
16
128
Integer Registers
128
Floating Point Registers
Instruction Pointer
64
Predicate Registers
User Mask
8
Branch Registers
128
Application Registers
CPUID Registers
Current Frame Pointer
Performance Monitor
Data Registers
Figura 1: set di registri itanium
• R2-R3:scratch
• R4-R7:riservati
• R8-R11:valori di ritorno delle procedure
• R12:stack pointer
• R13:(Riservato)Thread Pointer
• R14-R31:scratch
• R32-R128:General registers
Gli scratch registers sono quelli usati per scopi general purpose, quando una
procedura usa pochi registri vengono usati questi registri. Il registro R0 sempre uguale a zero é uno stratagemma, usato anche in altri processori, per poter
ottenere l’indirizzamento assoluto semplicemente usando l’indirizzamento base+displacement e usando come base R0. Cosı́ implementando pochi modi di
indirizzamento, se ne possono ottenere altri derivati da questi. I registri R32R128 sono general purpose e possono essere usati dalle procedure che usano piú
di 2 o 3 registri e che quindi non hanno abbastanza registri di scratch.
0.3.2
Register Stack
Dato il gran numero di registri era necessario un meccanismo per gestirli al
meglio, perché non tutte le procedure usano i registri da R32 a R128, ed era
0.3. MECCANISMI INNOVATIVI DI ITANIUM
Registri R32
Proc A
R40
Local
R50
R55
R60
R68
Output
Proc B
Input
Local
Proc C
Output
Input
Proc B
Proc A
17
Input
Local
Local
Local
Output
Output
Figura 2: chiamate a procedura
necessario permettere alla funzione di usufruire solo dei registri necessari. In
altri processori la procedura standard prevedeva che o il chiamante o il chiamato (caller o calle) salvassero il valore dei registri nello stack per permettere
alla funzione di usarli. Con tutti questi registri diventava un pó complicato
e inefficiente questo metodo di procedere. In Itanium si usa un altro metodo
chiamato Regiter Stack I registri da R32 a R128 vengono usati come uno stack.
Ogni funzione ha a disposizione 3 tipiú di registri:
• Input registers
• Local registers
• output registers
Gli input sono i registri usati per i parametri in ingresso, i Local sono quelli
usati internamente dalla funzione. I registri di output non sono quelli usati per
i valori di ritorno come potrebbe sembrare dal nome, ma sono quelli usati dalla
funzione per passare parametri ad altre sottofunzioni. Si ricorda che i registri
per passare i valori di ritorno sono R8-R11. I registri di output del chiamante
coincidono con i registri di input del chiamato. Bisogna considerare i registri
R32-R128 come uno stack ogni funzione alloca sullo stack il numero di registri
che gli occorrono. input, local e output sono solo denominazioni diverse per i
registri general purpose e, una volta compilato il codice, vengono mappati sui
registr r32-r128. Essi servono per facilitare la scrittura del codice. esempio: In
figure 1.2 si puó vedere come cambia lo stack regisers con 3 procedure A, B,
C che vengono chiamate una dentro l’altra. All’inizio lo stack registers punta
al registro R32, la procedura A alloca sullo stack register 8 registri Local, cioé
da usare internamente, e 10 registri output per passare i parametri di input
18
ala procedura B. Quando la procedura B viene chiamata, essa consapevole di
dover ricevere in input 8 parametri e alloca sullo stack registers 8 registri di
input piú 5 registri che userá internamente, e altri 5 registri per poter passare
i parametri di input alla procedura C. Si puó notare come i registri di output
di A e quelli di input di B coincidano; questo permette di passare i parametri
da una funzione all’altra. C, a sua volta, alloca 5 registri di input e 8 registri
local. Come si puó notare C non usa registri di output perché non deve chiamare
sotto di sé nessun’altra procedura. All’istruzione di return di una funzione il
puntatore dello stack registers torna indietro alla funzione precedente. In questo
modo si elimina la necessitá di salvare i registri che la funzione userá perché
necessario solamente che la funzione allochi con l’istruzione ALLOC dei registri
sullo stack. Una domanda che sorge spontanea é : se dopo chiamate a procedura
successive magari ricorsive si allocato un numero di registri che vá oltro R128
cosa succede? Itanium se si arriva fino a R128 e sono necessari altri registri
usa un meccanismo per salvare i registri e liberare spazio sullo stack dei registri
per la funzione successiva. Questa operazione abbastanza costosa in termini di
colpi di clock puó durare anche 20 colpi di clock e deve essere quindi evitata
accuratamente se le prestazioni sono essenziali. D’altronde il numero di registri
é tale da far sı́ che il processore non debba mai salvare i registri per liberare
spazio sullo stack.
0.3.3
Software pipeline
I meccanismi di software pipeline non sono stati da me approfonditi piú di
tanto perché non li ho utilizzati; daró comunque un’idea generale del loro funzionamento perché in alcuni casi, sono meccanismi molto utili e innovativi. Il
software pipeline é applicato quando nel software ci sono dei blocchi di codice
uguale ripetuti piú volte, come nel caso dell’algoritmo DES in cui ci sono 16
round. L’idea del software pipeline é quella di usare una pipeline applicata al
software. Per esempio nel caso del DES ogni round dovrá svolgere delle operazioni specifiche: Espansione E, trasformazione tramite S-boxes, ecc. L’idea
é quella di mettere i vari round in pipeline, cioé mentre il primo round sta
eseguendo la sua seconda operazione, il secondo esegue la prima e cosı́ via. Tuttavia nel caso di algoritmi crittografici ogni round dipende dal precedente, di
conseguenza il secondo round non puó iniziare prima della fine del primo. Per
questo motivo questi meccanismi non sono stati utilizzati nell’ottimizzazione.
La pipeline viene attuata grazie al register stack, il meccanismo descritto sopra.
Si usano dei registri virtuali. Ogni ciclo usa un determinato numero di registri
( ad esempio il primo utilizza i registri dall’R32 al R41, dall’R42 all’R51 ecc).
Per esempio per il ciclo uno il virtual register 1 corrisponde al registro R32, per
il ciclo 2 il virtual register 2 corrisponde al registro R42. Potendo usare diversi
registri i cicli possono essere eseguiti insieme.
0.3.4
Speculation and Predication
Prediction
Il meccanismo di Prediction serve per ottimizzare le condizioni tipo if-else presenti nel codice. Quando nel codice si trovano delle condizioni, queste vengono
predette dalla branch prediction unitá con meccanismi complessi illustrati dopo,
0.3. MECCANISMI INNOVATIVI DI ITANIUM
19
if(R1)
R2=R2+R4;
else
R7=R2-R5;
Figura 3: condizione tipo if-else
cmp. eq p1,p2=r1,r0
(p1)br. cond else_clause
add r2=r2,r4
br end_if
else_clause:
sub r7=r2-r5
end_if:\linebreak
Figura 4: codice assembler if-else
cmp.ne p1, p2=r1, r0
(p1)add r1=r2, r4
(p2)sub r7=r2, r5
Figura 5: codice assembler if-else trasformato con predicati
ma non detto che vengano predette nel modo esatto. Ogni condizione che non é
predetta esattamente, porterá a una perdita di colpi di clock, poiché le istruzioni
caricate non sono quelle esatte e si deve eseguire un’altra parte di codice. La
perdita é proporzionale alla lunghezza della pipeline, perché quando si ha una
prediction errata la pipeline viene svuotata e si perderanno tante piú istruzioni
quanta la sua lunghezza. Siccome la pipeline di Itanium é lunga 8 stages il numero distruzioni che vengono perse puó essere significativo. Nello pseudocodice
in figura 1. 3 c’é una condizione sul registro R1. Se é vera si esegue il codice
R2=R2+R4, altrimenti il codice R7=R2-R5. La condizione sará predetta con i
meccanismi sopra descritti. Se la condizione su R1 é predetta in modo erroneo si
perdono fino a 10 clock. I prediacati sono un modo per permettere al processore
di eseguire o ignorare delle istruzioni. Si basano sull’uso dei predicate registers
che sono lunghi 1 solo bit e valgono o TRUE o FALSE. I predicati precedono le
istruzioni in questo modo:
(p1)R2=R3+R4
L’istruzione R2=R3+R4 verrá eseguita solo se il valore di p1 é TRUE cioé
1, altrimenti l’istruzione verrá considerata come una nop e ignorata. Il codice
esempio di prima che tradizionalmente era compilato come in figura 1.4
La prima istruzione di compare paragona R1 con R0 che vale sempre 0, se
é vera setta P1=1 e P2=0. L’istruzione successiva br(branch) verreseguita sole
se P1 uguale a 1 ciose R1==0. Questo modo di procedere anche nel caso di
un codice cosı́ semplice porta a una perdita di colpiú di clock, perché anche
20
se il codice é lungo solo due colpiú di clock considerando che la condizione é
predetta in modo erroneo il 30% delle volte si ottiene una lunghezza media di
(2 clock+(30%*10clock)=5. Trasformando il codice compiú lato con i predicati
come in figura 1.5.
In questo modo sono stati eliminati i salti nel codice e il processore semplicemente ignorerá le istruzioni che non devono essere eseguite . Il codice
durerá sempre 2 colpi di clock senza avere nessun ritardo causato da un’erronea
previsione del branch.
Parte II
Assembler Itanium
21
Capitolo 1
Descrizione dell’assembler
Itanium
1.1
Formato delle istruzioni
Le istruzioni vengono scritte nella forma:
ISTR R1=R2, R3
R1 é l’operando destinazione, R1 e R2 sono gli operandi sorgente. Le istruzioni
Itanium hanno molti modificatori, alcuni per la dimensione delle istruzioni(per
esempio load 4 bytes o 8 bytes), altri che definiscono delle ulteriori indicazioni
per l’istruzione. I modificatori possono essere trovati o attaccati all’istruzione
come per esempio nel caso della load :ld4 o ld8, oppure separati dall’istruzione da
un punto, come per esempio ld8.fill.sa. L’assembler Itanium offre una grande
varietá di istruzioni con molti modificatori disponibili in modo da offrire al
programmatore la possibilitdi controllare anche i comportamenti piú sottili del
processore e dell’architettura. Un esempio sono le istruzioni che permettono di
controllare la cache.
1.2
Registri
Dato l’alto numero di registri i nomi dei registri sono molti, e alcuni registri
hanno anche 2 denominazioni. Molti non hanno accesso diretto dal programma,
ma vengono usati e modificati solo dal processore. I general purpose registers
sono i registri piú usati. Gli application registers sono registri che controllano
le funzioni del processore piú svariate, dal mascheramento degli interrupt, alla
scelta dell’uso di memory reference big o little endian, al controllo del register
stack. Qui verrá soltanto analizzato luso dell’application register ar.pfs; per
approfondimenti si rimanda a [2]. Il registro ar.pfs viene usato per controllare
il register stack engine, ovvero il meccanismo che controlla il register stack.
I Control Registers servono per memorizzare lo stato del processore e i suoi
parametri.
23
24
CAPITOLO 1. DESCRIZIONE DELL’ASSEMBLER ITANIUM
REGISTERS TYPE
General purpose registers
Floating-point registers
Application registers
Control Registers
Instruction TLB traslation registers
Data TLB translation registers
Predicate Registers
NOTAZIONE ASSEMBLER
r
f
ar
cr
itr
dta
p
ACCESSO INDIRETTO
Y
Y
Tabella 1.1: principali registri Itanium
1.3
Procedure
Le procedure in assembler Itanium vengono scritte in questo modo:
1
2
3
4
5
6
7
8
9
10
.text
.global encrypt
.proc funzione_di_encrypt
encrypt:
alloc loc0=ar.pfs, 3, 20, 0, 0
...
istruzioni
...
br. ret.sptk.many b0;;
.endp funzione_di_encrypt
La riga 2 serve a rendere visibile all’esterno la funzione encrypt, dichiarandola
global. La procedura viene aperta dalla riga 3, e viene chiusa dalla riga 10. La
riga 4 é l’entry point, il punto a cui si salta quando viene chiamata la procedura. L’istruzione alla riga 5 alloca sullo stack 20 registri local e 3 registri di
input. Per ulteriori informazioni sull’istruzione alloc vedi la sezione istruzioni
principali. L’istruzione alla riga 9 é l’istruzione di ritorno, i vari modificatori
vengono spiegati nella sezioni istruzioni. All’interno della procedura, al posto di
usare i registri Rxx, si possono utilizzare i registri In, loc e out; questo facilita
la scrittura del codice. Al posto dei puntini del codice precedente potrá quindi
trovare istruzioni del tipo:
mov
xor
add
mov
loc2=in0
loc2=loc2,loc3
loc3,loc2,loc5
out1=loc3
Si ricorda che i registri out non servono per passará e i valori di ritorno, ma solo
per passará e i valori in input alle procedure. Per passará e i valori di ritorno si
usano i registri r8-r11.
1.4
Explicit Bundle
Quando si scrive l’assembler Itanium si puó porre uno stop implicito al processore; questo significa che tutte le istruzioni dopo lo stop verranno eseguite nel
colpo di clock successivo. Lo stop espresso con ;; esempio:
1.4. EXPLICIT BUNDLE
xor
add
and
sub
25
loc2=loc2, loc3
loc3,loc2,loc5;;
loc7=loc20,loc21
loc5=loc4,loc19
Il processore esegue le prime due istruzioni in un colpo di clock, dopodiché
incontra lo stop ed esegue le altre 2 istruzioni nel colpo di clock successivo.
E’ possibile scrivere l’assembler con Bundle espliciti, ovvero si puó comunicare
al processore come le istruzioni verranno codificate ed eseguite. Ogni Bundle
composto da tre slot, cio3 istruzioni; il processore puó eseguire al massimo 2
bundle alla volta, ovvero 6 istruzioni. I Bundle vengono indicati con parentesi
graffe . All’inizio del Bundle si puó scivere il tipo di Bundle. esempio:
{. mmi
add loc3, loc2, loc5
add loc7=loc7,loc8
xor loc2=loc2,loc3
}
{. mmi
ld4 loc9=[loc9]
ld4 loc10=[loc10]
shr loc11=loc11,3
}
Qui sono indicati 2 boundle, entrambi di tipo memory-memory-integer. In ognuno ci sono 3 istruzioni che devono essere nel posto giusto allinterno del Bundle.
Ad esempio, le istruzioni Integer vanno all’ultimo slot. Per ulteriori informazioni su come avviene l’esecuzione o i vari tipi di Bundle vedere la sezione
Architettura.
26
CAPITOLO 1. DESCRIZIONE DELL’ASSEMBLER ITANIUM
Capitolo 2
istruzioni principali
2.1
1
2
3
4
Add
add r1=r2,r3
add r1=r2,r3,1
adds r1=imm14,r3
addl r1=imm22,r3
La add ha la forma o add registro registro come in 1, o add registro immediato
come in 3. In 2 l’operazione svolta r2+r3+1. Ci sono 2 forme per gli add con
immediati, perché Itanium distingue tra immediati di lunghezze diverse. La
causa di questo é il formato delle istruzioni. Anche se ogni istruzione viene
codificata sempre su 41 bit, i campi cambiano, e in alcune istruzioni é possibile
inserire immediati solo di certe dimensioni. Qui si distingue tra immediati di
14 bit o minori, e quelli di al max 22 bit. Se si deve sommare una costante con
piú di 22 bit bisogna prima caricare la costante con una movl in un registro.
2.2
Alloc
1 alloc r1=ar.pfs,i,l,o,r
La alloc alloca sullo stack register il numero di registri richiesto che risulta la
somma di i+l+o. i sta per registri di input, il numero di registri in cui vengono
passate le funzioni. l sta per local, il numero di registri usati internamente dalla
procedura. o sta per output, il numero di registri usati per passare paramatri
alle sottoprocedure. R sta per rotating, controlla il meccanismo di rotazione
dei registri. Vedere Register Rotation per approfondimenti. In questo caso r é
sempre posto a zero. ar.pfs é l’application register che controlla lo stack engine,
ovvero il meccanismo di register stack. esempio:
alloc loc1=ar.pfs,2,10,0,0
Questa istruzione alloca sullo stack register 12 registri, di cui i primi due sono
usati per ricevere i parametri di ingresso, 10 sará anno usati internamente alla
funzione. I registri disponibili per la procedura saranno loc1-loc13.
27
28
CAPITOLO 2. ISTRUZIONI PRINCIPALI
2.3
1
2
And
and r1=r2,r3
and r1=imm8,r3
Quando si usano delle costanti, la massima lunghezza della costante é di 8 bit,
oltre bisogna caricare la costante in un registro con una movl ed usare la forma
1.
2.4
Cmp-Cmp4
Compare e Compare 4 bytes sono le due istruzioni di compare, compare 4 byte
é usata per confrontare i valori a 32 bit. Esistono molti modificatori per queste
2 operazioni. Ci sono modificatori per i valori con segno, senza segno e che
determinano come i predicate register verranno settati. La forma base
1
2
cmp.crel p1, p2=r2,r3
cmp4.crel p1, p2=r2,r3
crel puó essere eq per equal, ne per non equal, lt per low than, ecc. Vengono
confrontati i due valori contenuti in r2 e r3. Le istruzioni settano i due predicate
registers p1 e p2 a seconda che la condizione sia vera o falsa. Se la condizione é
vera p1 e posto a 1, se é falsa p1 posto a 0. P2 vienesettato sempre all’inverso
di p1, se p1 vale 1 p2 vale 0 e viceversa. I due predicate registers possono poi
essere messi nel codice precedendo le istruzioni. esempio:
(p1) add loc7=loc7,loc5
(p2) add loc7=loc7,loc6
A seconda che la condizione sia vera o falsa loc7 sará sommato o loc5 o loc6.
2.5
Dep
1 dep r1=r22,r3,pos6,len4
dep. z r1=r2,pos6,len6
Deposit serve per prelevare da un registro un gruppo di bit che iniziano al bit
0, di lunghezza specificata da len4, per poi depositarli in un altro registro alla
posizione indicata da pos4. puó essere utile in alcuni casi, l’unico problema che
la lunghezza del gruppo di bit che vengono depositati al massimo espressa su 4
bit, ed il gruppo di bit quindi al massimo di 15 bit. Se si vuole fare deposit di
un numero di bit superiore non c’é modo. La seconda versione dep.z azzera i
bit del registro destinazione e ha valori di pos e len su 6 bit.
2.6
1
2
Extr
extr r1=r3,pos6,len6
extr.u r1=r3,pos6,len6
2.7. LD
29
Extract, al contrario di dep, estrae un gruppo di byte da un registro e li mette
in un altro registro a partire dal bit 0. Il gruppo di bit di lunghezza len6 e inizia
in posizione indicata da pos6. Questa istruzione molto utile perché permette
di selezionare dei bit da un registro, operazione molto comune negli algoritmi
crittografici. L’unico punto a sfavore é che se ne puó eseguire solo una per colpo
di clock.
2.7
Ld
La load ha molte forme e molti modificatori; questi permettono di specificare
quanti byte devono essere letti da memoria, se la cache deve considerare il valore
caricato come di uso frequente oppure no, se la cache deve fare l’advance load
della word successiva al valore caricato in vista di una load uleriore o no, e cosı́
via. I modificatori non verranno presentati qui. Per approfondimenti consultare
[1].
1
2
3
ldsz r1=[r3]
ldsz r1=[r3],r2
ldsz r1=[r3],imm9
sz sta per size; puó valere 4, 8 o 16, indicati quanti nyte sono letti. In tutte e
tre le forme l’indirizzo contenuto in r3. In 2 il valore di r3 aggiornato dopo la
load, sommando r2. In 3 dopo la load a r3 viene sommato un immediato di 9
bit. Le ultime 2 forma sono di autoincremento.
2.8
1
2
3
4
5
6
Nop
nop imm21
nop.i imm21
nop.b imm21
nop.m imm21
nop.f imm21
nop.x imm62
La nop é molto importante perché usata per riempire gli slot vuoti. Quando
si hanno meno di 3 istruzioni per formare un bundle si possono usare delle
nop per arrivare a tre istruzioni e usará e l’explicit bundling. Gli immediati
sono ignorati dal processore, possono servire solamente come demarcazione in
punti del programma. Esistono differenti tipi di nop; la prima solo una pseudo
operazione e viene mappata su una delle successive. Ogni nop puó andare ad
occupare un’unitá funzionale diversa, una unitá integer o di branch, oppure di
memory, oppure di floating point o una x unitá .
2.9
Mix-Mux
Per queste istruzioni si rimanda al mauale Intel [1].
30
CAPITOLO 2. ISTRUZIONI PRINCIPALI
2.10
1
2
3
4
Shl
Shr r1=r3,r2
shr.u r1=r3,r2
shr r1=r3,count6
shr.u r1=r3,count6
Lo shift Left semplicemente shifta a destra R3 di n posizioni pari al contenuto
di R2 o dell’immediato count su 6 bit.
2.11
1
2
Shr
Shl r1=r3,r2
shr r1=r3,count6
Lo shift Right semplicemente shifta a destra R3 di n posizioni pari al contenuto
di R2 o dell’immediato count su 6 bit.
2.12
R2
Shrp
R3
R1 Figura 2.1: Shrp
1
shrp r1=r2,r3,coun6
shif right pair é un’operazione molto utile: serve per eseguire i rotate fissi sia a
destra che a sinistra. I due operandi r2 e r3 sono affiancati e considerati come
un unico blocco di 128 bit; da questo blocco vengono selezionati 64 bit, a partire
dalla posizione specificata da count6, e messi in un altro registro, come si puó
vedere in figura 2.1. Per ottenere uno shift fisso, bisogna avere il valore da
routare da 32 bit in r2. Si deve mettere lostesso valore in r3, ma nella parte
alta del registro. Cosda avere, una volta eseguita la shrp, il valore da routare 2
volte affiancato. Poi in count6 si mette un valore pari a 32+il numero di bit di
cui si vuole il rotate a sinistra oppure 32-il numero di bit di cui si vuole il rotate
a destra. In r3 nei primi 32 bit si avrá il valore routato dei bit voluti. Unica
accortezza é quella di azzerare i bit da 32 a 64 di r3, (quando necessario).
2.13. XOR
2.13
1
1
31
Xor
xor r1=r2,r3
xor r1=imm8,r3
I due operandi sorgente sono r2 e r3 e quello destinazione r1, in caso di immediato la limitazione é che l’immediato deve essere su al massimo su 8 bit.
32
CAPITOLO 2. ISTRUZIONI PRINCIPALI
Parte III
Ottimizzazione degli
Algortimi
33
2.14. INTRODUZIONE
2.14
35
Introduzione
In questa parte verranno presentati gli algortimi ottimizzati. La parte degli
algortmi é strutturata in modo da permettere una lettura piú semplice o una
piú approfondita. Per ogni algoritmo vi é prima una parte che descrive in modo generale le caratteristiche dell’algortimo e le ottimizzazioni eseguite. Nella
sezione successiva, chiamata ottimizzazione in dettaglio, vengono forniti maggiori dettagli, e vengono anche presentate e spiegate parti di codice assembler.
La sezione Ottimizzazioni in Itanium riassume il lavoro svolto specificatamente
per Itanium, traendo le conclusioni finali. Nel capitolo linee generali vengono
introdotti dei metodi di ottimizzazione generali, validi per tutti gli algortimi e
sono illustrate le situazioni che si incontrano spesso in tutti gli algoritmi.
36
Capitolo 3
Linee generali
3.1
Ottimizzazione generale del codice
Le parti del codice che subiscono ritardi e su cui si puó operare un’ottimizzazione
sono,in generale, le seguenti:
• load-store
• cicli tipo for o while
• jump
3.1.1
Load-Store
Il discorso sulle load vale per tutte le architetture su cui si usano le load, in
generale nei processori RISC. Le load dalla memoria impiegano minimo 2 colpi
di clock per essere eseguite; questo vuol dire che,dopo la load ,deve passare un
colpo di clock prima di poter usare il valore caricato. Questo colpo di clock
andrá sprecato. Il modo per risolvere il problema é anticipare il piú possibile le
load, in modo tale da avere i valori caricati dalla memoria il prima possibile. Non
tutte le load saranno anticipabili nel codice perché questo dipende da quando
l’indirizzo a cui fa riferimento la load disponibile nel codice. Nel caso in cui
l’istruzione di load e quella che ne usa il risultato siano vicine, il colpo di clock
tra le due istruzioni deve essere riempito con istruzioni che non siano dipendenti
dalla load, e far sı́ che possano essere eseguite prima del completamento della
load. esempio:
1 xor R45=R45, R39
2 ld4 R40=[R40];;
3 xor R42=R40,R41
4 add R45=R45,R46
5 sub R47=R47,R50;;
6 xor R45=R45,R47;;
Dopo la Load ci sará un colpo di clock in cui il processore non usato perché
l’istruzione successiva di xor usa R40 che é il risultato della load. Si puó notare
come le istruzioni 4 e 5 non dipendano dalla load. Il codice eseguito in 4 colpi
di clock. Trasformando il codice cosı́
37
38
CAPITOLO 3. LINEE GENERALI
1 xor R45=R45, R39
2 ld4 R40=[R40];;
3 add R45=R45,R46
4 sub R47=R47,R50;;
5 xor R42=R40,R41
6 xor R45=R45,R47;;
Il buco dopo la load é stato riempito con le due istruzioni e il codice eseguito in
3 colpi di clock. Per le store il discorso é inverso; esse possono essere posticipate
nel codice, ed eseguite quando si hanno degli slot liberi.
3.1.2
Cicli e loop unrolling
Il classico ciclo del tipo:
for i=1 to 10 do
a[i]=a[i-1]+b
c=c+f
Quando questo ciclo compilato per ogni iterazione del ciclo verrá perso minimo
un colpo di clock, perché al termine ci sará un’istruzione di compare che verifica
se si é arrivati alla fine del ciclo e ci sará un salto al codice iniziale per una
nuova iterazione. In realtá dipendentemente dall’architettura, si perderanno
molti piú colpiú di clock tanto piú é lunga la pipeline. Essendo la pipeline
Itanium molto lunga, si perderanno anche 10 colpi di clock per iterazione. La
soluzione il loop unrolling, cioil codice viene srotolato, invece che usare il for
si scrivono esplicitamente le varie iterazioni del ciclo, in modo da eliminare i
branch al fondo di ogni iterazione. esempio:
iterazione 1
a[1]=a[0]+b
c=c+f
iterazione 2
a[2]=a[1]+b
c=c+f
iterazione 3
a[3]=a[2]+b
c=c+f
iterazione 4
a[4]=a[3]+b
c=c+f
. . .
. . .
Il loop unrolling dá anche un’altra opportunitá perché ora che abbiamo le operazioni una dopo l’altra si puó sfruttare il parallelismo del codice operando uno
scheduling sulle istruzioni, ovvero riordinando ed eseguendo quante piú operazioni possibili in parallelo. Ci sono due tipi di cicli: i cicli in cui le varie iterazioni
sono dipendenti le una dalle precedenti, e quelle in cui sono invece indipendenti
tra di loro. Il caso di prima quello in cui un’iterazione del ciclo dipende dalla precedente. piú le iterazioni sono indipendenti, piú si avrá parallelismo nel
codice e piú si avrá beneficio dal loop unrolling e dall’ottimizzazione.
3.2. OTTIMIZZAZIONE DELL’ASSEMBLER
3.2
39
Ottimizzazione dell’assembler
Quando si ha un codice assembler, quello che limita il parallelismo e la velocitá
del codice sono :
• dipendenze di dato
• dipendenze di nome
• dipendenze di controllo
Le dipendenze di dato sono quelle in cui un’istruzione ha come operando un
input un valore che l’output di una precedente operazione, quindi tra le due c’é
una dipendenza di dato. esempio:
XOR R40=R40,R42
ADD R41=R40,R46
Sono proprio queste dipendenze per cui non si puó fare nulla; esse sono indipendenti dall’architettura su cui viene compilato il codice e limitano il parallelismo
del codice. Le dipendenze di nome sono quelle in cui due istruzioni usano lo
stesso registro, ma non c’é dipendenza di dato tra le due. esempio:
XOR R40=R41,R42
ADD R41=R39,R32
Queste dipendenze possono essere evitate nella scrittura del codice semplicemente cambiando il nome ai registri coinvolti. In particolare in Itanium, dato il
gran numero di registri, non si verificano spesso dipendenze di questo tipo. Le
dipendenze di controllo sono quelle relative ai branches. Un’istruzione dentro
ad un if é dipendente dalla condizione dell’if e dal branch che eventualmente
verreseguito. E’ utile,dove possibile, trasformare le dipendenze di controllo in
dipendenze di dato. In Itanium ,per risolvere questo problema, esiste il meccanismo di Predication, che grazie ai predicati, come spiegato nell’apposita sezione,
permette al processore di eseguire o meno delle istruzioni.
3.3
Fasi di Ottimizzazione degli Algoritmi
Per Ottimizzare gli algoritmi di openssl sono state eseguite le seguenti fasi:
1. Stdio approfondito dell’algoritmo
2. scelta dell’implementazione
3. traduzione in assembler dello pseudocodice o codice C
4. debug
5. ottimizzazione e riordinamento del codice
6. debug
40
CAPITOLO 3. LINEE GENERALI
Lo studio dell’algoritmo ha lo scopo di capire le caratteristiche principali dell’algoritmo e il suo funzionamento. La fase successiva prevede di scegliere tra
le varie implementazioni dell’algoritmo quella che piú si adatta all’architettura Itanium, e se necessario apportare delle modifiche a queste implementazioni
che sono scritte in pseudocodice o in C. Scelta l’implementazione, questa viene
tradotta in assembler Itanium, dopo che si sono scelte le istruzioni da usare. In
alcuni casi sono state eseguite prove con differenti versioni di codice assembler
per vedere quale risultava il piú efficiente. Un esempio é la permutazione iniziale
del DES, di cui sono state realizzate 2 versioni: una usando l’istruzione extr. u
e l’altra usando solo shift+and. Attraverso una lunga fase di Debug, nella quale
vengono testati i vari spezzoni di codice uno per uno per poi essere montati
insieme, si arriva ad una versione funzionante del codice assembler. A questo
punto il codice non ancora ottimizzato, anzi, puó addirittura risultare piú lento
del codice in C. Nella fase di ottimizzazione vengono apportare le ultime modifiche al codice per renderlo piú veloce possibile e soprattutto vengono riordinate
le istruzioni e racchiuse in budles. La fase di scrittura del codice e quella di
ottimizzazione non sono del tutto separate, perché mentre si scrive il codice si
cerca di scriverlo giá ottimizzato o comunque pronto per esserlo in un ulteriore
fase. La fase di riordinamento del codice é essenziale e deve essere eseguita con
cura, perché si rischia di perdere colpi di clock solo invertendo l’ordine di due
istruzioni.
3.4
3.4.1
Operazioni presenti in tutti gli algoritmi
Uso di Costanti
Gli algoritmi usano spesso costanti da sommare o mettere in xor. Di solito queste
sono costanti a 32 bits. Dato l’alto numero di registri disponibili, é conveniente
caricarle all’inizio dell’algoritmo in un registro e mantenerle, in modo da non
doverle piú ricaricare. Per questo si usa l’istruzione movl(move long). esempio:
movl R50,0x0000000034b56a76
L’istruzione movl usa 2 slot all’interno del bundle; per questa ragione é meglio
usarla in uno spazio del codice in cui c’é uno spazio libero di 2 slot. E’ facile che
si generi uno split issue se non posizionata bene. Di solito si usa in un bundle
con prima un’istruzione Ingeger o ALU. ES:
{
xor R43=r44,R45
movl R50,0x0000000034b56a76
}
3.4.2
Selezione di bits da registro
Un’operazione molto comune consiste nel dover selezionare un gruppo di bits da
un registro. Questa operazione é eseguita di solito con uno shift + un and. Co
lo shift si porta il gruppo di bits da selezionare in basso nel registro, con l’and e
una maschera opportuna si selezionano solo i bits che occorrono. Per esempio,
per selezionare i bits dal 20 al 26 del registro R40. Le operazioni da compiere
sono:
3.4. OPERAZIONI PRESENTI IN TUTTI GLI ALGORITMI
41
Shift right R40 di 20 posizioni
and R40,0x3f
Su Itanium, poiché i registri sono da 64 bit, per poter eseguire un and con una
maschera piú lunga di 22 bit si deve caricare la maschera in un registro con una
movl. Un altro modo per selezionare i bits dato dall’uso dell’istruzione extr.
Questa é studiata apposta per selezionare un insieme di bits da un registro e
posizionarli in un altro registro. Sembrerebbe che con una sola istruzione si
possa eseguire il tutto. In realtá quando le selezioni di bits da registro sono
molte (come accade negli algoritmi esaminati), l’uso di extr. u non é molto
conveniente. La questione che extr.u é eseguibile solo dall’unitá funzionale I0, e
quindi una sola extr.u puó essere eseguita per colpo di clock. Usando shift+and,
gli shift possono essere eseguiti dalle unitá funzionali I0 e I1, quindi si possono
eseguire 2 shift per colpo di clock. In ogni caso si eseguono al massimo 2 selezioni
di bits da registro ogni 2 colpi di clock. In molti casi ho preferito usare gli shift
perché sono piú facilmente riorganizzabili e pongono meno limitazioni, mentre
gli extr.u sono molto limitativi in quanto possono essere eseguiti solo da una
unitá funzionale.
3.4.3
Look up in tabella
Per eseguire il look up in tabella c’é bisogno dell’indirizzo base di questultima;
esso sará caricato in un registro, dopodiché é necessario un displecement che sará
sommato alla base. Itanium supporta solo le load in cui l’indirizzo contenuto
in un registro, quindi non si possono usare modi di indirizzamento complicati
come base+displecement, ma i due valori vanno sommati preventivamente. Il
valore base della tabella va dichiarato nella sezione data, per esempio se il nome
della tabella é Te0:
. data
. global Te0#
successivamente si carica l’indirizzo in un registro, si puó sommare il displacement e caricare il valore da memoria:
movl R50=Te0#
add 51=0xf, R50
ld4 R51=[R51]
3.4.4
Uso delle load
E’ frequente dover caricare da memoria valori tutti contigui in memoria. E’ il
caso delle chiavi dei round. Solitamente le chiavi dei round sono posizionate in
uno struct e i loro valori sono contigui in memoria. Siccome Itanium dispone di
load dalle varie dimensione, si possono usare load4 che carica 32 bits, load8 che
carica 64 bits ma anche load16 che carica 128 bits dalla memoria. Poi, una volta
caricati i valori, se erano necessarie unitá da 32 bits, basterá dividere i blocchi.
In realtla regola é quella di usare una load sempre della dimensione minima
necessará ia. Se si lavora su dati a 32 bit meglio usare load4 e non load8. Il
problema é che finché si usano load4, l’accesso alla cache non avrá problemi.
Quando si usano le load8, gli accessi a memoria devono essere allineati a 8
bytes. La cache supporta accessi non allineati in qualche caso, ma si rischia
42
CAPITOLO 3. LINEE GENERALI
di incappare in una penalitá in termini di colpi di clock persi. Considerando
anche il fatto che Itanium permette 2 load per colpo di clock, se si usano valori
a 32 bit, non c’é ragione di usará e load8, a meno che non sia strettamente
necessario e si sia assolutamente certi che i valori da caricare siano allineati. Un
esempio concreto stato quello di rc5: lo struct che conteneva le chiavi del round
strutturato in questo modo:
typedef struct rc5_key_st
{
int rounds;
RC5_32_INT data[2*(RC5_16_ROUNDS+1)];
} RC5_32_KEY;
Come si puó vedere, nello struct prima delle chiavi contenute in data c’é un int
di 32 4 bytes. La versione iniziale di RC5 usava le load8. Siccome le chiavi si
trovano dopo un int, sono sfasate tutte di 4 bytes, usando le load8, ci saranno
degli accessi non allineati in memoria. Il risultato é stato che il codice era
piú lento di quello originale. Modificando il codice e usando le load4 il codice
risultava piú veloce. In questo caso si era perso circa il 15-20 % delle prestazioni.
E’ molto importante non mischiare load4 con load8.
3.4.5
Xor tra una serie di valori
A volte nel codice sono presenti linee di questo genere:
A=A^B^C^D^E^F^G
Questo codice sará compilato in modo da eseguire uno xor alla volta. In realtá ,
siccome lo xor é un’operazione che gode di proprietá commutative e associative,
il codice sopra puó essere eseguito in 3 colpi di clock invece che in 6. Se si
ipotizza che i valori di A, B, C. . siano contenuti nei registri R40, R41, R42,
R43, R44, R45, R46, Il codice puó essere riscritto come:
1 clock
xor R40=R40,R41
xor R48=R42,R43
xor R49=R44,R45
2 clock
xor R40=R40,R48
xor R49=R49,R46
3 clock
xor R40=R40,R49
Dato il gran numero di registri disponibili in Itanium é opportuno usare piú
registri e risparmiare colpi di clock.
3.4.6
Htonl Ntohl
In tutti gli algoritmi c’é il problema di interpretare le word o come host order o
come network order. Per trasformare una word da host order a network order
e viceversa, i singoli byte devono essere scambiati di posto nella word in questo
modo:
3.4. OPERAZIONI PRESENTI IN TUTTI GLI ALGORITMI
43
host order:
B1 B2 B3 B4
network order: B4 B3 B2 B1
Per eseguire tale operazione normalmente si usano degli shift piú or. In Itanium
ci sono delle istruzioni particolari come la mux. Queste istruzioni fanno esattamente questa operazione. Quindi, per convertire da host to network order e
viceversa, l’ideale é usare l’istruzione
mux1
3.4.7
R32=R33,@rev
Uso dei bundles per le istrzioni assembler
Si puó usare sia l’explicit Boundling che l’implicit Boundling. Con l’implicit
Boundling il compilatore deciderá i boundling, i dual issue e gli split issue.
Usando l’explicit Boundling, si ha il pieno controllo sul processore, si sa quale istruzione verrassegnata a quale unitá funzionale, si sa quando il processore
caricherun nuovo bundles, e quali istruzioni verranno eseguite in un dato colpo
di clock. Se si decide di usará e i Bundles, é preferibile racchiudere in Bundles
TUTTE le istruzioni del codice, non soltanto quelle piú critiche. E’ sconsigliabile mischiare istruzioni racchiuse in Bundles con operazioni non racchiuse in
Bundles. Questo perché il compilatore in alcuni casi inserisce uno split issue
anche dove non serve, e tutto il lavoro di perfezionamento del codice é inutile
se si perdono colpi di clock in questo modo. Inoltre, é anche difficile vedere
dove il compilatore ha inserito lo split issue, perché bisogna operare con un debugger sul codice compilato e controllare linea per linea se il codice come ce lo
aspettavamo. Per esempio se inserisco un codice di questo tipo:
{. mii
load4 R40,[R40]
xor R41=R41,R42
shr R43=R43,2
}
xor R44=R44, R48;;
Tutte queste istruzioni possono essere eseguite nello stesso colpo di clock perché
non hanno dipendenze fra di loro. Come si vede le prime tre sono racchiuse
in un bundle e l’ultimo xor no. E’ il caso in cui si é mischiato un bundle con
operazoni non in bundle. Siccome lo xor é un’operazione che puó essere eseguita
sia dalle unitá Integer che dalle unitá di memoria, lo xor puó realmente essere
eseguito nello stesso clock perché ci sono ancora unitá di memoria disponibile.
sarebbe ragionevole aspettarsi che il compilatore compiú li il codice posizionando
le istruzioni per essere eseguite in un solo colpo di clock. Invece il compilatore
compila il codice per essere eseguito in due colpi di clock in questo modo:
load4 R40,[R40]
xor R41=R41,R42
shr R43=R43,2 ;;
xor R44=R44,R48;;
44
CAPITOLO 3. LINEE GENERALI
Questo perché interpreta lo xor come istruzione Integer, e poiché le due unitá
integer erano giá occupate dalle precedenti istruzioni di xor e shr, inserisce uno
stop implicito ;;. Per questo c’é uno split issue. Per essere sicuri di come il
codice verreseguito quindi preferibile usará e solamente l’explicit Boundling. Il
codice corretto il seguente:
{. mii
load4 R40,[R40]
xor R41=R41,R42
shr R43=R43,2
}
{. mmf
xor R44=R44,R48
nop. m 0
nop. f 0
}
uso di NOP
I nop risultano molto utili per l’uso di explicit Boundling; perché ogni volta non
ci sono tre istruzioni per formare un Boundle si useranno dei nop per riempire
gli spazi vuoti.
3.5
Regole Generali per Itanium
I punti di forza di Itanium che devono essere sfruttati per l’ottimizzazione sono:
1. Gran numero di unitá funzionali
2. Efficiente architettura per l’accesso in memoria
3. Gran numero di registri
4. Architettura totalmente a 64 bit
5. vasto set di itsruzioni
Dato il gran numero di unitá funzionali e il gran numero di registri, si deve
cercare di sfruttare tutto il parallelismo presente nel codice. Si deveno cercare
di usare piú registri per poter compiere piú operazioni possibili in parallelo, fino
ad arrivare ad eseguire 6 istruzioni per colpo di clock. L’architettura potente
per l’accesso in memoria, dispone di ben 4 porte per l’accesso, 2 per le load e
2 per le store, quindi si possono eseguire 2 load e 2 store per colpo di clock.
Si deve cercare, in un codice in cui sono presenti molte load, di usare tutte le
porte disponibili. Grazie all’architettura a 64 bit, quelle operazioni che prima
erano dispendiose ora risultano piú semplici. In realtá tutti gli algoritmi da me
analizzati non fanno uso dellarchitettura a 64 bit. Il vasto set di istruzioni puó
essere sfruttato, laddove conveniente, usando operazioni specifiche di Itanium,
che migliorino le prestazioni.
Capitolo 4
DES
4.1
Caratteristiche Principali
Le caratteristicge principali del DES sono:
• unitá fondamentale a 32 bit
• permutazioni
• espansioni
• s-boxes
• i round lavorano su 2 blocchi da 32 bit
• poco parallelismo nel codice, molte dipendenze di dato
L’algoritmo DES é un algoritmo che non presenta molto parallelismo nel
codice, quindi non otterrá un gran aumento di prestazioni quando eseguito su
Itanium, anche se ottimizzato.
4.1.1
Permutazioni
Le permutazioni non sono operazioni semplici, e siccome i processori general purpose non le supportano, devono essere ottenute da una serie di altre istruzioni
piú semplici come shif, and e xor. Questa serie di operazioni atte ad ottenere
una permutazione non sono da eseguire in contemporanea, bensı́ una istruzione deve essere effettuata di seguito all’altra. Questo non permette di trarre
alcun vantaggio dal gran numero di unitá funzionali di Itanium, perché una,
o al massimo due istruzioni sará anno eseguite contemporaneamente, mentre
Itanium puó effettuare anche 6 istruzioni simultaneamente. L’unica possibilitá
di ottimizzazione sulle permutazioni é quella di ridurre il numero di operazioni
da eseguire usando delle istruzioni ad-hoc presenti in Itanium. In conclusione,
non possibile ottimizzare molto le permutazioni, al massimo si puó ottenere un
miglioramento intorno al 10%.
45
46
4.1.2
CAPITOLO 4. DES
32 bit-64 bit
L’algoritmo DES prende in input un blocco da 64 bit ; questo blocco viene diviso
in due blocchi di bit ognuno da 32 bit. Su questi 2 blocchi da 32 bit l’algortimo
esegue le sue operazioni. Di conseguenza, l’unitá fondamentale dell’algoritmo é
un blocco da 32 bit. Anche se Itanium dispone di registri a 64 bit, questi non
possono essere sfruttati in quanto l’agoritmo lavora internamente su blocchi a
32 bit.
4.1. CARATTERISTICHE PRINCIPALI
4.1.3
47
Table look-up
Il modo piú veloce per eseguire l’oprazione di s-boxe é utilizzare un table lookup in tabella. Questa tabella non é nient’altro che una matrice di byte in cui si
entra con 6 bit selezionati da un registro da 32 bit e questa restituisce il risultato
dell’s-boxe. poiché per fare table look-up si deve eseguire un accesso in memoria,
é possibile sfruttare la capacitá di Itanium che é in grado di compiere 2 load da
memoria nello stesso colpo di clock. In questo modo la velocitá di esecuzione
dell’algoritmo verrá migliorata.
Input
m1
m64
Initial Permutation
IP
L0
R0
K1
F
L1
R1
K2
F
Rounds 2−15
L15
R15
k16
F
L16
R16
FP
Inverse Permutation
Output
c1 c2..
c64
Figura 4.1: struttura dell’algoritmo DES
48
4.2
4.2.1
CAPITOLO 4. DES
Ottimzzazione DES in Dettaglio
Initial Permutation e Final Permutation
58
60
62
64
57
59
61
63
50
52
54
56
49
51
53
55
42
44
46
48
41
43
45
47
IP
34
36
38
40
33
35
37
39
26
28
30
32
25
27
29
31
18
20
22
24
17
19
21
23
10
12
14
16
9
11
13
15
2
4
6
8
1
3
5
7
Tabella 4.1: DES Initial Permutation
40
39
38
37
36
35
34
33
8
7
6
5
4
3
2
1
48
47
46
45
44
43
42
41
16
15
14
13
12
11
10
9
IP
56
55
54
53
52
51
50
49
24
23
22
21
20
19
18
17
64
63
62
61
60
59
58
57
32
31
30
29
28
27
26
25
Tabella 4.2: DES Final Permutation
Essendo queste due operazioni eseguite solo all’inizio e alla fine, esse non
sono cosı́ decisive per l’ottimizzazione, in quanto nell’economia dell’algoritmo
la cosa piú importante é ottimizzare i 16 round. La permutazione iniziale a
anche quella finale che sono una l’inverso dell’altra prendono in input 64 bit e li
trasformano in output in 64 bit. Sembrerebbe necessario compiere operazioni sui
singoli bit per ottenere le due permutazioni; in realtá possono essere scomposte
in operazioni che agiscano su gruppi di bit. Benché la permutazione sia su 64
bit, non si riesce ad ottenere un gran vantaggio usando registri a 64 bit. Questo
perché tale permutazione é un’operazione molto complessa. Personalmente non
ho trovato un modo per suddividerla in una serie di operazioni semplici su 64
bit, al massimo si puó suddividere la permutazione con una serie di operazioni
su 32 bit. L’IP(Initial Permutation) puó essere suddivisa in 5 passi piú semplici,
come illustrato in figura 4.2. Su 32 bit queste 5 fasi erano ottenute usando uno
stratagemma per scambiare i bit da tra un registro ed un altro, sfruttando il
fatto che dati due registri R1 e R2:
R1^R2^R1=R2
e
R2^R1^R2=R1
Su Itanium la soluzione migliore é quella di usare maschere e shift. Il miglioramento di prestazioni é circa del 10%.
4.2. OTTIMZZAZIONE DES IN DETTAGLIO
49
Input Block
m1 m2 m3 m4 .....
..m63 m64
R0
L0
m1 m2..
m32
m33 m34
m64
FASE 1
R0
R0
R0
R0
R0
L0
FASE 2
L0
FASE 3
L0
FASE 4
FASE 5
Figura 4.2: 5 Fasi dell’Initial Permutation
L0
L0
50
CAPITOLO 4. DES
E
32
4
8
12
16
20
24
28
1
5
9
13
17
21
25
29
2
6
10
14
18
22
26
30
3
7
11
15
19
23
27
31
4
8
12
16
20
24
28
32
5
9
13
17
21
25
29
1
Tabella 4.3: DES Expansion E
P
16
29
1
5
2
32
19
22
7
12
15
18
8
27
13
11
20
28
23
31
24
3
30
4
21
17
26
10
14
9
6
25
Tabella 4.4: DES permutation P
4.2.2
16 Rounds
I 64 bit di output dell’Initial Permutation sono divisi in due blocchi da 32 bit R
e L. R viene espanso secondo la tabella E da 32 a 48 bit per poter essere messo
in xor con la chiave del round di 48 bit. Il risultato é diviso in 8 gruppi da 6 bit
ciascuno, e viene eseguita l’operazione di s-boxe. Ogni gruppo viene mandato
ad un s-boxe diverso: il primo gruppo all’S-boxe 1 il secondo all’S-boxe 2 e cosı́
via. I 6 bit b1, b2..b6 vengono usati per indicizzare la tabella S-BOX in questo
modo: le row vengono ottenute cosı́ row=2*b1+b6, le column sono ottenute
considerando b2b3b4b5 come la rappresentazioni di un numero c su 4 bit, cio
c compreso tra 0 e 16. Ognuno degli 8 S-boxe dá in output 4 bit, in totale si
ottengono 32 bit. Questi 32 bit vengono permutati secondo la tabella P. Per
maggiori dettagli consultare [3]. Le ottimizzazioni sul round sono le seguenti:
Si puó notare che nell’espansione E ogni bit compare al max due volte. Questo
vuol dire che un singolo bit di R messo in xor al massimo con 2 diversi bit
della chiave. Inoltre si puó notare che se in E si considerano le righe pari e
poi le dipari separatamente come illustrato nella tabella. Sia nelle righe pari
sia in quelle dispari i bit di R non si ripetono mai e sono disposti in maniera
crescente. Dalla tabella 4.5 si puó capire come i valori delle righe pari e dispari
siano semplicemente i valori di R shiftati di 1 a destra nelle pari, perché queste
iniziano col bit 32, e shiftati di 4 a sinistra nelle righe dipari perché queste
iniziano col quarto bit di R. Quindi, invece di mettere E(R) in xor con la chiave,
si puó mettere 2 volte R in xor con la chiave. Anche la chiave deve essere disposta
in modo giusto perché il risultato sia uguale a prima. Il risultato di questo xor
sará 64 bit invece che 48 bit, ma di questi 64 ne verranno selezionati 48 al
4.3. RISULTATI
32
8
16
24
1
9
17
25
E pari
2
3
10 11
18 19
26 27
51
4
12
20
28
5
13
21
29
4
12
20
28
5
13
21
29
E dispari
6
7
8
14 15 16
22 23 24
30 31 32
9
17
25
1
Tabella 4.5: Righe pari e disperi di E
momento di eseguire gli S-Boxes. In breve, prima avevo 48 bit e li raggruppavo
in 6 bit dal bit 1 al bit 5, dal bit 6 al bit 11, dal bit 12 al bit 18, ecc; ora devo
selezionarli da 64 bit ma le operazioni sono identiche, perché si tratta sempre
di shift + and.Ho applicato l’espansione E invece che 16 volte sui round 1 volta
sulla chiave. In questo modo si evitata l’espansione E nei round. Per maggiori
chiarimenti consultare [4] Abbiamo visto come debbano essere selezionati 6 bit
alla volta da un registro. Itanium offre un’operazione dedicata a questo scopo,
l’extr.u(extract unsigned), che permette di estrarre un numero di bit arbitrario
in una posizione arbitraria da un registro e metterli in un altro registro. Tutto
questo evita un’operazione, infatti nel modo tradizionale avremmo dovuto usare
uno shift + un and. L’unico inconveniente é dato dal fatto che Itanium puó
eseguire solo un extr. u per colpo di clock, quindi, in definitiva, usare un metodo
o l’altro non cambia di molto le cose. Usando Extr.u risparmio un colpo di clock,
pereseguo un Extr.u per clock; usando shift + and ci metto 2 colpi di clock ma
posso farne 2 in contemporanea. Un’altra ottimizzazione data dall eseguire
l’operazione di S-boxes prima, seguita poi dall’espansione P sul risultato degli
S-boxes. Queste 2 operazioni possono essere fuse in un unica azione. Quando si
accede alla tabella di look up per gli S-boxes, in output invece che il risultato
dell’S-boxe soltando, c’é il risultato dell’S-boxe gipermutato secondo P.
4.2.3
Ottimizzazione in Itanium
In questa sezione si riassumono le ottimizzazioni peculiari apportate al DES su
Itanium. Per quando riguarda L’IP e la FP sono state usate istruzioni assembler
proprie di Itanium come l’istruzione mix.1 che hanno portato ad un miglioramento di circa il 10%. Per quanto riguarda i round l’uso di istruzioni assembler
proprie di Itanium come la Extr.u non ha portato benefici. Nei 16 round si é
cercato di sfruttare al massimo la capacitdi accedere a memoria di Itanium, cioé
impaccando e sistemando le operazioni in modo da sfruttare al massimo le 2 load
per colpo di clock disponibili. In questo modo ogni round é stato migliorato di
circa il 10%. In conclusione, l’algoritmo per la sua struttura interna a 32 bit e
per la presenza di poco parallelismo nel codice, non trae particolare beneficio
dall’architettura Itanium.
4.3
Risultati
Le prestazioni sono state migliorate di circa il 10%. Mentre il codice C compilato
impiegava 9.19 secondi per eseguire 167772160 volte la funzione DES, il codice
ottimizzato impiega 8.27 secondi. I risultati del test di velocitá openssl non
vengono riportati perché sussiste ancora un problema nel linking tra codice C
52
CAPITOLO 4. DES
e codice assembler, che porta il codice ottimizzato a non essere piú veloce del
codice C, ma questo non dipende dal codice, ma dal compilatore.
Capitolo 5
RC5-32/12/16
5.1
Caratteristiche Principali
Le caratteristiche principali sono:
• semplicitá
• uso di rotate variabili
• uso di add
• poco parallelismo nel codice, molte dipendenze di dato
L’algortimo RC5 é molto semplice, le uniche istruzioni usate sono add, xor e
rotate variabili. Come si vedrá piú avanti le operazioni in un round sono una
dipendente dalla precedente, il parallelismo é molto scarso. Inoltre in Itanium
non c’é un’istruzione che corrisponda allo shift variabile. Non vi é un particolare
vantaggio prestazionale su Itanium, anzi, c’é da porre la massima attenzione alle
somme che sono da eseguire in modulo 232 su registri da 64 bit.
5.1.1
Rotate variabili
In Itanium 2 non c’é il supporto per i rotate variabili. L’unico supporto é quello
per i rotate fissi, con l’istruzione shrp, come spiegato nella sezione istruzioni. I
rotate variabili devono essere ottenuti usando 2 shift, uno xor e un sxt o zxt(vedi
istruzioni).Il risultato é che uno shift variabile eseguito in 4 colpi di clock.
5.1.2
Add modulo 232
Per eseguire le add modulo 232 con operandi su 32 bit, bisogna fare attenzione,
perché essendo i registri a 64 bit, laddove su registri a 32 bit il risultato di una
somma di due numeri positivi generava un overflow e dá ı́ come risultato un
numero negativo, ora su 64 bit tale risultato non sará negativo benspositivo,
poiché lo spazio é diventato modulo 264 . La soluzione é quella di usare le
istruzioni sxt4 o zxt4 a seconda dei casi che, ripetitivamente, estendono il segno
o mettono a zero i bit dal trentaduesimo in poi del registro. Di conseguenza,
per ogni add esiste un’operazione supplementare da eseguire.
53
54
CAPITOLO 5. RC5-32/12/16
5.2
Ottimzzazione RC5-32/12/16 in Dettaglio
A=A+S[0]
B=B+S[1]
for i=1 to r do
A=((A^B)<<B)+S[2*i];
B=((B^A)<<A)+S[2*i+1];
<< =rotate variabile
A e B sono i due blocchi da 32 bit bit in cui diviso l’input block da 64 bit
S il vettore con le chiavi per round
Figura 5.1: RC5 pseudocodice dell’algoritmo
5.2.1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
RC5-32/12/16 single round
xor loc3=loc3,loc2
and loc9=0x1f,loc2;;
sub loc1=32,loc9
shl loc4=loc3,loc9;;
shr loc10=loc3,loc1;;
or loc8=loc4,loc10;;
add loc8=loc8,loc14
and loc3=loc8,loc15;;
ld4 loc14=[in1],4
xor loc2=loc2,loc3
and loc1=0x1f,loc3;;
sub loc4=32,loc1
shl loc9=loc2,loc1;;
shr loc10=loc2,loc4;;
or loc11=loc9,loc10;;
add loc11=loc11,loc13;;
and loc2=loc11,loc15
ld4 loc13=[in1],4;;
//A^B
//seleziono i 5 low bit di B
//sottraggo da 32 il valore 5 low bit di B
//shift left per il rotate
//shif right per il rotate
//or dei due shift
//somma (a^B)<<B + S[1]
//azzero bit 32-64 di A
//load di S per il prossimo round
//B^A
//seleziono 5 low bit di A
//sottraggo da 32 i 5 low bit di A
//shift left dper secondo rotate
//shift roght per secondo rotate
//or dei due shift
//somma di (B^A)>>a + S[2]
//azzero bit 32-64 di B
//load di S per il prossimo round
Figura 5.2: RC5 single round
Le operazioni piú dispendiose nel round sono i rotate variabili. Eseguire
A << B significa ruotare A di un numero di posizioni pari ai 5 bit meno significativi di B. Per fare questo devo quindi selezionare i 5 bit meno significativi
di B mettendo B in and con la maschera 0x1f. Guardando il codice e lo pseudocodice, le righe 1-8 del codice assembler corrispondono alla prima riga dentro
il for dello pseudocodice. Alla riga uno c’é l’operazione (AB ), le righe dalla 2
alla 6 sono il rotate (AB ) << B. La settima riga é la somma con S[2]. S[2] é il
loc14 e il suo valore era giá stato caricato precedentemente. L’ottava riga é un
5.2. OTTIMZZAZIONE RC5-32/12/16 IN DETTAGLIO
55
and per selezionare solo i primi 32 bit di A, perché dopo la somma, come detto
in precedenza, dato che i registri sono a 64 bit ci possono essere dei bit oltre il
trentadiesimo che devono essere eliminati o si deve estendere il segno. Nella riga
9 e 19 si caricano i valori di S per il round successivo. Dalla riga 10 alla 18 vi
é l’aggiornamento di B che corrisponde nello pseudocodice alla seconda riga del
for. Come si puó notare le operazioni per colpo di clock sono al massimo due,
quindi viene usata un terzo della capacitá di esecuzione di Itanium. L’ottimizzazione che é stata portata consistenell’eseguire nel round precedente le load di
S di quello successivo, in modo da avere i valori di S giá pronti e non perdere
ulteriori colpi di clock. Non é possibile anticipare altre operazioni del round
successivo nel round precedente, perché le istruzioni successive sono dipendenti
dalle precedenti. Questo dato anche dal fatto che RC5 in un round aggiorna sia
A che B.
5.2.2
Ottimizzazioni in Itannium
Data la semplicitá dell’algoritmo, non c’é rano particolari ottimizzazioni da
eseguire nello pseudocodice. Le ottimizzazioni nello scrivere l’assembler sono
state quelle di anticipare al round precedente le load di S per il round succesivo.
Da notare che siccome S é un vettore di valori da 32 bit tutti contigui, invece
che usará e le load4 che caricano 32 bit alla volta avrei potuto usare le load8
che caricano 64 bit alla volta e dimezzare le load. Questa operazione non é
conveniente perché in questo modo non si risparmiamo colpi di clock ma si rischia
solo di incorrere in un accesso alla cache disallineato che viene penalizzato in
termini di colpi di clock. Vedi Linee guida.
56
5.3
CAPITOLO 5. RC5-32/12/16
Risultati
rc5
20971520 times on 16 size blocks
5242880 times on 64 size blocks
1310720 times on 256 size blocks
327680 times on 1024 size blocks
40960 times on 8192 size blocks
Time
14. 6s
13. 94s
13. 76s
13. 71s
13. 7s
Tabella 5.1: rc5-openssl speed results
type
rc5
16 bytes
22982. 49k
64 bytes
24070. 61k
256 bytes
24385. 49k
1024 bytes
24474. 42k
8192 bytes
24492. 29k
Tabella 5.2: rc5-openssl speed results
rc5
20971520 times on 16 size blocks
5242880 times on 64 size blocks
1310720 times on 256 size blocks
327680 times on 1024 size blocks
40960 times on 8192 size blocks
Time
11. 08s
10. 43s
10. 24s
10. 19s
10. 18s
Tabella 5.3: rc5-optimized code speed results
type
rc5
16 bytes
44267. 06k
64 bytes
46995. 00k
256 bytes
47527. 52k
1024 bytes
47662. 55k
Tabella 5.4: rc5-optimized code speed results
8192 bytes
47527. 52k
Capitolo 6
SHA-1
6.1
Caratteristiche Principali
Le caratteristiche principali dell’algortimo sono:
• epsansione di 128 bit a 640 bit.
• uso di rotate fissi
• molto parallelismo nel codice
• in ogni round vengono aggiornati solo 2 dei 5 registri usati
• uso di molti registri per massime prestazioni
L’algortimo SHA1 riceve in input un numero di bit arbitrario, li considera 128 bit
alla volta e produce in output una stringa da 128 bit. I round sono 80, quindi
l’obbiettivo principale ottimizzare al massimo la durata di un round, perché
risparmiare anche un solo colpo di clock per round significa risparmiare 80 colpi
di clock. Le operazioni dei round possono essere parzialmente sovrapposte, in
modo da risparmiare ulteriori colpi di clock. I registri utilizzati sono molti,
perché piú cresce il parallelismo del codice, piú si avrá necessitá di usare piú
registri. Questo perché i vari round che sono eseguiti in parallelo devono usare
ognuno un diverso set di registri. Altra particolaritá é che in ogni round vengono
coinvolti 5 registri in input, ma solo 2 di essi vengono aggiornati, gli altri restano
uguali per il round successivo. Questo fa sı́ che alcuni registro debba mantenere
il proprio valore per 4 round, portando ad un aumento nel numero di registri
usati. Inoltre Come si puó vedere dal codice presente il openssl dal file sha locl
l’espansione delle word inizia con il round 16. Anche l’espansione eseguita in
parallelo con il codice che elabora le word ha bisogno di altri registri per poter
lavorare. Oltre alle operazioni semplici, quali xor and ecc., l’algortimo usa rotate
fissi. Itanium ha il supporto per i rotate fissi con l’uso dell’istruzione shrpair.
Ulteriori spiegazioni verranno fornite in seguito.
57
58
6.2
6.2.1
CAPITOLO 6. SHA-1
Descrizione dell’algoritmo e ottimizzazione
Descrizione dei round
Come si puó vedere dallo pseudocodice in figure 6.1 l’algoritmo é composto da
80 round. Ci sono 4 gruppi di round:dall’1 al 20, dal 21 al 40, dal 41 al 60, dal 61
all’80. Questi 4 gruppi si differenziano solamente per le costanti usate e per la
funzione F, G, H che cambia in ogni gruppo. I round hanno tutti una struttura
simile, prendono in input 5 valori e li elaborano. Guardando il codice in figura
6.2, in cui BODY 00 15 é una macro per un round definita sopra, si puó notare
la struttura dell’algortimo. I valori in input al primo round sono A, B, C, D, E,
T. I valori aggiornati in questo round, come si vede dal codice di BODY 00 15,
sono quelli di T e di B, gli altri valori restano uguali. Al round successivo i valori
vengono semplicemente passati in input a BODY 00 15 shiftati di una posizione
a destra; il secondo round riceve in input T, A, B, C, D, E. Questa struttura
si ripete per tutti i round. La struttura puó essere semplificata come in figura
6.3. Dai colori si puó notare come i valori iniziali di colore nero perdurino fino
al round 4 perché E resta tale fino al quarto round. Al settimo round i valori in
input saranno di nuovo come quelli del primo(anche se modificati nel corso dei
round). Il blocco base composto da 6 round. Usando registri giusti nei rounnd
giusti si puó usare un blocco base di 6 round.
6.2.2
Espansione delle word
L’espansione delle word che nello pseudocodice in figura 6.1 era eseguito prima
di tutti i round, viene eseguito solo quando necessario, per risparmiare tempo.
L’espansione genera le word dalla 17 alla 79; poiché le word vengono usate in
ordine una per round, la diciassettesima word non sará usata prima del diciassettesimo round, ed é per questo che le espansioni nel codice openssl iniziano al
round 16. Per ogni espansione di una word vengono usati 6 colpi di clock, ma
questi possono avvenire in contemporanea con l’algoritmo che elabora le word
round per round. In realtá il codice openssl compilato perde comunque dei colpi
di clock per eseguire le espansioni delle word. Quello che si é cercato di fare invece nel codice assembler é far iniziare le espansioni delle word prima, al secondo
round, e tenere i valori del vettore X in 16 registri fin da subito, in modo da
eseguire le espansioni perfettamente in parallelo all’altro codice usando le unitá
funzionali libere. Questo stratagemma si puó vedere passando dalla versione
finale non ottimizzata dell’algoritmo a quella ottimizzata, in cui le espansioni
prima eseguite in blocchi a parte, vengono ora mischiate al codice dei round
ed assorbite cosı́ dall’algortimo. In questo modo si sono risparmiati 2-3 colpi
di clock per round. La difficoltá di inserire il codice delle espansioni in mezzo
all’altro codice é data dalla lunghezza finale del file, 1800 righe circa. E’ necessario quindi distribuire il codice su 1800 righe prestando attenzione ai registri
usati e cercando di non intralciare le istruzioni del codice dei round.
6.3. OTTIMIZZAZIONE SHA-1 NEL DETTAGLIO
6.3
6.3.1
59
Ottimizzazione SHA-1 nel dettaglio
Singolo Round
Per eseguire il rotate fisso di un regisrto si usa l’istruzione shrpr, come illustrato
nella sezione istruzioni. Analizzando per esempio i round 1 e 2, si puó notare
come nel primo l valore A é usato ruotato di 5, nel secondo A é ruotato di 30.
Queste operazioni si ripetono in tutti i round. Per risparmiare colpi di clock,
quando nel primo round si sono settati i due registri per l’istruzione shrpair,
si ruota A di 5 e anche A di 30, ovvero si eseguono 2 shrpair su A. Il secondo
risultato verrá usato successivamente. Dal momento che, come si puó vedere in
figura 6.3 molti valori in input rimangono invariati in output al round, alcune
delle operazioni del round successivo, possono essere eseguite in anticipo. Un
esempio é dato dall rotate di prima. Altro esempio l’operazione nel secondo
round E=ROTATE(T, 5)+f(A, B, C)+D+X2+Y1. La load di X2 puó essere
fatta in anticipo, Y2 una costante, C e D non vengono modificato nel primo
round. Con questi valori si puó eseguire anticipatamente giá nel primo round
la somma X2+Y1+D, cosı́ , per aggiornare E, resterá da sommare nel secondo
round il ROTATE(T, 5) e f(A, B, C). Si puó quindi raggiungere una parziale
sovrapposizione tra un round e quello successivo.
6.3.2
Espansione delle word
Le word vengono tenute nei registri R34-R50, escluso R36. Per i round 116 i registri R34-R50 contengo le word X[0]-x[15], per i round 16-32 le word
contengono le word X[16]-X[31] e cosı́ via. L’espansione delle word la cui parte
di codice si puó vedere in figura 6.4 puó venire mischiata, come giá spiegato
in precedenza, al codice dei round. La parte difficile consiste nel far usare
all’espansione delle word dei registi non usati in quel momento dal codice dei
round. Il tutto complicato ulteriormente perché l’espansione della word 1 puó
sovrapporsi con quella della word 2 o della word 3 e cosı́ via. In pratica, si
inserisce il codice dell’espansione ovunque ci sia una unitá funzionale lasciata
libera dal codice dei round. Nella versione finale del codice le istruzioni marcate
con etichette del tipo ESP1 34 2 sono le istruzioni di espansione. E’ vero che
Itanium ha 6 unitá funzionali, ma ha solo 2 unitá Integer, quelle usate per
eseguire le istruzioni integer, quali sono gli shift a shrpair. Il limite maggiore
quindi causato da queste due unitá funzionali, perché Itanium non puó eseguire
piú di due shift per clock e non piú di un shrpair per clock.
6.3.3
Ottimizzazione in Itanium
SHA-1 é un algoritmo con molto parallelismo all’interno, di conseguenza é stato
possibile sfruttare tutte e 6 le unitá funzionali di Itanium. In questo modo i colpi
di clock impiegati per l’espansione delle word sono quasi totalmente assorbiti
all’interno del codice dei round, risparmiando il 20% dei colpi di clock. Un altro
10% é stato guadagnato sovrapponendo in parte il codice di un round e quello del
round successivo. E’ stato possibile grazie al fatto che in un round si aggiornano
solo 2 valori di quelli in input al round, cosche alcune operazioni del round
successivo(quelle che operano sui valori non modificati dal precedente round)
possono giá essere eseguite nel round precedente. Grazie a queste migliorie si
60
CAPITOLO 6. SHA-1
é ottimizzato il tempo di esecuzione di SHA-1 di circa 32% rispetto al codice
openssl originale.
6.4
Risultati
SHA1 128
10485760 times on 16 size blocks
2621440 times on 64 size blocks
655360 times on 256 size blocks
163840 times on 1024 size blocks
20480 times on 8192 size blocks
Time
6. 04s
5. 96s
5. 96s
5. 94s
6. 00s
Tabella 6.1: SHA-1:openssl speed results
type
SHA1 128
16 bytes
27776. 85k
64 bytes
28149. 69k
256 bytes
28149. 69k
1024 bytes
28244. 47k
8192 bytes
27962. 03k
Tabella 6.2: SHA-1:openssl speed results
SHA1 128
10485760 times on 16 size blocks
2621440 times on 64 size blocks
655360 times on 256 size blocks
163840 times on 1024 size blocks
20480 times on 8192 size blocks
Time
4. 43s
4. 42s
4. 41s
4. 40s
4. 45s
Tabella 6.3: SHA-1:optimized code speed results
type
SHA1 128
16 bytes
37871. 82k
64 bytes
37957. 50k
256 bytes
38043. 57k
1024 bytes
38130. 04k
8192 bytes
37701. 61k
Tabella 6.4: SHA-1:optimized code speed results
Nelle tabella sono riportati i risultati ottenuti compilando il codice di SHA-1
senza e con il codice assembler Itanium. LA funzione implementata in assembler
Itanium SHA1 BLOCK HOST ORDER é stata migliorata del 26,6%. Il codice C impiegava 6.04 secondi per eseguire 10485760 volte la funzione, il codice
assembler impiega 4.43 secondi.
6.4. RISULTATI
1-Definizione di costanti
h1, h5=5 costanti iniziali
y1, y4=4 costanti additive per round
2- Pad
in input riceve una bitstring di lunghezza b>=0
si aggiunge un pad per arrivare ad un input
composto da 16*m 32-bit words:x0, x1, x2. . . . x16m-1.
3-Inizializzione
(H1, H2, H3, H4, H5) <- (h1, h2, h3, h4, h5)
4-Esapnsione:
di definisce un vettore di 80 word X[80]
si copiano le prime 16 word di input in x[0]-x[15]
for j=16 to 79 do:
Xj<-((Xj-3^Xj-8^Xj-14^Xj-16)<<-1)
(dove <<-1 sta per shift left di uno(
5-Processing
inizializziamo le variabili usate
(A, B, C, D, E)<-(H1, H2, H3, H4, H5)
t variabile temporanea
le funzioni f, h, g sono:
f(B, C, D) = ((C^D)&B) ^D
h(B, C, D) = B^C^D
g(B, C, D) = (B&C) | ((B|C)&D)
(Round 1)for j=0 to 19 do
t<-((A<<-5)+f(B, C, D)+E+Xj+y1)
(A, B, C, D, E)<-(t, A, B<<-30, C, D)
(Round 2)for j=20 to 39 do:
t<-((a<<-5)+h(B, C, D)+E+Xj+y2)
(A, B, C, D, E)<-(t, A, B<<-30, C, D)
(Round 3)for j=40 to 59 do:
t<-((a<<-5)+g(B, C, D)+E+Xj+y3)
(A, B, C, D, E)<-(t, A, B<<-30, C, D)
(Round 4)for j=60 to 79
t<-((A<<-5)+h(B, C, D)+E+Xj+y4)
(A, B, C, D, E)<-(t, A, B<<-30, C, D)
(H1, H2, H3, H4, H5)=<-(1+A, H2+B, H3+C, H4+D, H5+E)
6-Final
H1, H2, H3, H4, H5 costituiscono il risultato finale
Figura 6.1: Pseudocodice semplificato di SHA-1
61
62
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
CAPITOLO 6. SHA-1
#define BODY_00_15(i,a,b,c,d,e,t,xi) \
(t)=xi+(e)+K_00_19+ROTATE((a),5)+F_00_19((b),(c),(d)); \
(b)=ROTATE((b),30);
for (;;)
{
BODY_00_15( 0,A,B,C,D,E,T,X( 0));
BODY_00_15( 1,T,A,B,C,D,E,X( 1));
BODY_00_15( 2,E,T,A,B,C,D,X( 2));
BODY_00_15( 3,D,E,T,A,B,C,X( 3));
BODY_00_15( 4,C,D,E,T,A,B,X( 4));
BODY_00_15( 5,B,C,D,E,T,A,X( 5));
BODY_00_15( 6,A,B,C,D,E,T,X( 6));
BODY_00_15( 7,T,A,B,C,D,E,X( 7));
BODY_00_15( 8,E,T,A,B,C,D,X( 8));
BODY_00_15( 9,D,E,T,A,B,C,X( 9));
BODY_00_15(10,C,D,E,T,A,B,X(10));
BODY_00_15(11,B,C,D,E,T,A,X(11));
BODY_00_15(12,A,B,C,D,E,T,X(12));
BODY_00_15(13,T,A,B,C,D,E,X(13));
BODY_00_15(14,E,T,A,B,C,D,X(14));
BODY_00_15(15,D,E,T,A,B,C,X(15));
Figura 6.2: stralcio del file primi 15 round
6.4. RISULTATI
A
63
B
C
D
E
A
B
C
D
T
A
B
C
D=Rotate(E,5)+f(T,A,B)+C+X3+y1
E
T
B
A
D
C
ROUND 4
C=Rotate(D,5)+f(E,T,A)+B+X4+y1
E=Rotate(E,30)
C
ROUND 3
D
T=Rotate(T,30)
D
ROUND 2
E
E=Rotate(T,5)+f(A,B,C)+D+X2+y1
A=Rotate(A,30)
E
ROUND 1
T=Rotate(A,5)+f(B,C,D)+E+Xj+y1
B=Rotate(B,30)
T
T
E
T
A
B
ROUND 5
B=Rotate(C,5)+f(D,E,T)+A+X5+y1
D=Rotate(D,30)
B
C
D
T
E
B
ROUND 6
A=Rotate(B,5)+f(C,D,E)+T+X6+y1
B=Rotate(B,30)
A
A
C
D
E
T
I cambiamenti di colori rappresentano i valori che vengono aggiornati ad ogni round
Figura 6.3: Struttura dei primi 6 round di SHA-1
ROUND 7
64
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
CAPITOLO 6. SHA-1
//espansione
//X[0]
xor loc52=loc34,loc37
xor loc51=loc43,loc48;;
xor loc34=loc51,loc52;;
shl loc52=loc34,1
shr.u loc51=loc34,31;;
or loc34=loc52,loc51;;
sxt4 loc34=loc34
//X[1]
xor loc52=loc36,loc38
xor loc51=loc44,loc49;;
xor loc36=loc52,loc51;;
shl loc52=loc36,1
shr.u loc51=loc36,31;;
or loc36=loc52,loc51;;
sxt4 loc36=loc36
Figura 6.4: SHA-1 espansione di 2 word in Assembler Itanium
Capitolo 7
AES (Rijndael)
7.1
Caratteristiche Principali
• ottimizzazione che riduce l’algoritmo a look up in tabella
• unitá minima usata é il byte
• molto parallelismo nel codice
• uso di molte load
L’algortimo AES non ha una struttura semplice come per esempio RC5, ci
sono piú fasi e operazioni da svolgere sulle word in input. Tuttavia, grazie
ad un’ottimizzazione giá apportata da Rijndael stesso, l’algortimo si riduce a
look up in tabella e a shift + and per selezionare i bit per fare il look up.
Le caratteristiche dell’algortimo cosı́ implementato sono perfette per Itanium.
Come si puó vedere dal codice nel file AESround.s, s0, s1, s2, s3 sono i valori di
input, e Te1, Te2, Te3 sono le tabelle su cui fare look up, in un round ci sono
16 load(i 16 accessi nelle tabelle), e le righe 2, 4, 6, 8 del primo round possono
essere eseguite tutte in parallelo.
7.1.1
Scelta dell’implementazione
Tra le implementazioni di AES ci sono 2 filoni distinti, uno che esegue tutte le
operazioni di AES una per una e l’altro che invece usa i look up in tabella. Dal
momento che Itanium puó eseguire fino a 6 istruzioni per colpo di clock, anche
la prima soluzione avrebbe potuto andare bene, perché anche se il numero di
istruzioni sarebbe piú alto rispetto alla soluzione con i look up in tabella, si
potrebbero comunque eseguire 6 operazioni per clock. Usando invece i look up
in tabella e le load, il numero di istruzioni é minore, ma ogni load impiega 2
colpi di clock per caricare il valore dalla memoria. Tuttavia, siccome Itanium
puó eseguire 2 load per colpo di clock, cioé 2 look up in tabella per colpo di
clock, é stata scelta l’implementazione con i table look up che risulta la piú
veloce su Itanium.
65
66
CAPITOLO 7. AES (RIJNDAEL)
State
Cipher Key
Add Round Key
1−Sub Bytes
2−Shift Rows
3−Mix Colums
Round Key 0−9
Add Round Key
1−Sub Bytes
2−Shift Rows
Round Key 10
Add Round Key
Figura 7.1: AES-struttura dell’algortimo
7.2
Ottimizzazione AES nel dettaglio
L’algortimo ha 4 fasi distinte per ogni round:
1. Bytes Sub
2. Shift Row
3. Mix Column
4. Add Round Key
Sub Bytes
In questa fase l’input di 128 bit viene considerato 1 byte alla volta. Ogni byte
viene sostituito tramite look up in tabella S-BOX in figura 7.1. I primi 4 bit
vengono usati come coordinate X, gli ultimi come coordinate Y. Per esempio il
byte 0x13 verrá sostituito con 0x7d. In realtá queste trasformazioni sono operazioni sui campi di Galuoise, ma i dettagli matematici qui non sono importanti.
Quello che conta é che l’unitá minima di bit usata in questa fase é 8 bit, quindi
anche se l’algoritmo prende in ingresso 128 bit in realtá qui li considera byte
per byte.
7.2. OTTIMIZZAZIONE AES NEL DETTAGLIO
hex
0
1
2
3
4
5
6
7
8
9
a
b
c
d
e
f
x
0
63
ca
b7
04
09
53
d0
51
cd
60
e0
e7
ba
70
e1
8c
1
7c
82
fd
c7
83
d1
df
a3
0c
81
32
c8
78
3e
f8
a1
2
77
c9
93
23
2c
00
aa
40
13
4f
3a
37
25
b5
98
89
3
7b
7d
26
c3
1a
ed
fb
8f
ec
dc
0a
6d
2e
66
11
0d
4
f2
fa
36
18
1b
20
43
92
5f
22
49
8d
1c
48
69
bf
5
6b
59
3f
96
6e
fc
4d
9d
97
2a
06
d5
a6
03
d9
e6
67
S-BOX
Y
6
7
6f c5
47 f0
f7 cc
05 9a
5a a0
b1 5b
33 85
38 f5
44 17
90 88
24 5c
4e a9
b4 c6
f6 0e
8e 94
42 68
8
30
ad
34
07
52
6a
45
bc
c4
46
c2
6c
e8
61
9b
41
9
01
d4
a5
12
3b
cb
f9
b6
a7
ee
d3
56
dd
35
1e
99
a
67
a2
e5
80
d6
be
02
da
7e
b8
ac
f4
74
57
87
2d
b
2b
af
f1
e2
b3
39
7f
21
3d
14
62
ea
1f
b9
e9
0f
c
f3
9c
71
eb
29
4a
50
10
64
de
91
65
4b
86
ce
b0
Tabella 7.1: AES S-BOX
Shift Rows
Considerando l’output di 128 bit della prima fase diviso in 4 righe da 32 bit
ciascuna. Le 4 righe vengono ruotate a destra di 0, 1, 2, 3 byte rispettivamente,
come si vede in figura 7.2. L’unitá minima di bit usata qui é la riga cioé 32 bit.
[ht]
d4
27
11
ae
e0
bf
98
f1
b8
b4
5d
e5
1e
41
52
30
d4
bf
5d
30
e0
b4
52
ae
b8
41
11
f1
1e
27
98
e5
Tabella 7.2: AES Shift Rows
d4
02
03
01
01
04
bf
01 02
03
01
66
5d
01
01 02
03
81
30
03
01
01
02
e5
Figura 7.2: AES-Mix colums
Mix Colums
In questa fase il blocco di 128 bit viene considerato in 4 colonne di 32 bit
ciascuna. Ogni colonna moltiplicata per una matrice, con una moltiplicazione
d
d7
a4
d8
27
e3
4c
3c
ff
5d
5e
95
7a
bd
c1
55
54
e
ab
72
31
b2
2f
58
9f
f3
19
0b
e4
ae
8b
1d
28
bb
f
76
c0
15
75
84
cf
a8
d2
73
db
79
08
8a
9e
df
16
68
d4
d4
d4
d4
CAPITOLO 7. AES (RIJNDAEL)
x
x
x
x
02
01
01
03
+
+
+
+
bf
bf
bf
bf
x
x
x
x
03
02
01
01
+
+
+
+
5d
5d
5d
5d
x
x
+
x
01
03
02
01
+
+
+
+
30
30
30
30
x
x
x
x
01
01
03
02
=
=
=
=
04
66
81
e5
Figura 7.3: AES-Operazioni di Mix Colums
matriciale. Come si puó vedere dalla figura 7.2, i valori della matrice sono solo
3. Da questa moltiplicazione tra matrici, si puó notare come un singolo byte
darun contributo a tutti i byte della colonna in output. Per esempio il byte d4
verrá moltiplicato per 02 nelle prima riga, per 01 nella seconda e nella terza riga
e per 03 nella quarta riga. L’unitá minima usata qui é la colonna, cioé 32 bit.
Add Round key
In questa fase il blocco da 128 bit viene messo in xor con la chiave del round di
128 bit. Il codice di schedulazione delle chiave usa le stesse operazioni dell’algoritmo di Shift Rows e Sub-Bytes. La generazioni delle chiavi per i round non
verrá analizzta, perché non é essenziale per l’ottimizzazione in quanto interviene
una solo volta all’inizio dell’algoritmo.
Last Round
La differenza dell’ultimo round é che manca la fase di Mix xolumns.
7.2. OTTIMIZZAZIONE AES NEL DETTAGLIO
7.2.1
69
Ottimizzazione dell’algoritmo
Come descritto sopra nella fase di Sub Bytes, ogni byte viene sostituito con il
suo corrispondente tramite S-box. Nella seconda fase di shift Rows si cambiano
semplicemente le posizioni all’interno delle righe dei singoli byte, ma non vi é
nessuna sostituzione di valore dei bytes. Inoltre, un byte iniziale dopo le prime
2 trasformazioni contribuisce per un solo byte in output, non ci sono variazioni
nel numero di byte. Quindi, le prime due fasi possono anche essere invertite,
si puó eseguire prima la fase di Shift Rows e poi la fase di Sub Bytes. La
terza trasformazione di MixColums é anch’essa fissa e indipendente dall’input.
Guardando la figura 7.2, si osserva che la colonna in input di 4 byte viene
moltiplicata in successione per ogni riga della matrice per generare una nuova
colonna. Osservando la figure 7.3, considerandola per colonne, si vede che la
prima colonna é il primo byte in input, (d4), la seconda la prima riga della
matrice, la terza é il secondo byte in input, la quarta la seconda colonna della
matrice e cosı́ via. Di conseguenza, il primo byte moltiplicato per la prima
colonna della matrice, il secondo byte per la seconda colonna della matrice e
cosvia. Ogni byte in input da un contributo ad ogni riga di figura 7.3, cioé ogni
byte da un contributo per ognuno dei byte in uscita. Le operazioni di somma
nella figura 7.3 sono in realtá operazioni di somma senza riporto quindi degli
xor. poiché il primo byte in input della colonna in input subirá sempre le stesse
operazioni di moltiplicazione, e lo stesso accade per il secondo e anche per gli
altri due, si puó usare un look up in tabella che restituisca il risultato. Si usano
4 tabelle, una per ogni byte in input. In queste tabelle si entra in input con un
byte e si ritorna con 32 bits di risultato. Questi 32 bits di risultato corrispondono
in figura 7.3 alle colonne della figura. Ottenuti i 4 risultati dei 4 look up, questi
verranno messi in xor tra di loro (perché le somme sono degli xor)e sará ottenuta
la colonna di output. Ora sappiamo che la terza fase é ottenuta tramite table
look-up. Considerando le prime tre fasi in cui avevamo invertito le prime due,
si puó notare che un byte in input subirá nella prima fase un cambiamento di
posizione, ma non verrá modificato nel suo valore. Nella seconda e terza fase
subirá 2 trasformazioni di fila: una quella di Sub Bytes e, successivamente, il look
up in tabella della terza fase. Per ottimizzare ulteriormente, invece che eseguire
separatamente le 2 trasformazioni, queste si possono unificare in un unico look
up in tabella. A questo punto le tabelle usate per il look up prenderanno il
posto delle operazioni di S-Boxes e di Mix Colomns. Per ottenere la prima fase
di Shift Rows si usano degli shift + and per selezionare i bytes. La qarta fase di
Add Round Key é semplicemente uno xor con la chiave del round. Esaminando
ora nuovamente il codice nel file AESround.s si possonono capire le singole
operazioni. Le tabelle Te0, Te1, Te2, Te3 sono le tabella che fanno le operazioni
di Sub-Bytes e di Mix-Colums, gli shift ¡¡ sono le operazioni di Shift Rows e gli
and 0xff selezionano i vari bytes uno per uno. I risultati dei look up in tabella
sono poi messi in xor tra di loro, gli xor rappresentano le somme della figura
7.3. I valori sono poi direttamente messi in xor con la chiave del round kr[y].
L’ultimo round usa una tabella diversa, la tabella Te4, perché non c’é la fase di
Mix Columns.
70
7.3
CAPITOLO 7. AES (RIJNDAEL)
Ottimizzazione In Itanium
Data la forte presenza di look up in tabella e quindi di load, le potenzialitá
di Itanium riguardante gli accessi in memoria é sfruttata appieno. C’é molto
parallelismo nel codice, e questo permette di sfruttare tutte le unitá funzionali di
Itanium e di conseguenza la possibilitdi eseguire 6 operazioni per colpo di clock.
Il fatto che, pur ricevendo in input 128 bit, l’algoritmo li elabora byte per byte,
porta a non avere vantaggi dall’architettura a 64 bit di Itanium, e a non poter
sfruttare i registri a 64 bit. Per selezionare i singoli byte, operazione che nel
codice C é eseguita con shift e and, si potrebbero usare le istruzioni di extr.u,
ma poiché queste sono molto limitanti perché si puó eseguire un solo extr.u per
colpo di clock si é preferito usare gli shifts. Gli S-Boxes e la fase di Mix Columns,
usano come input per i table look-up un singolo byte, ottenendo in output 32
bit. Su Itanium si puó ipotizzare l’uso di tabelle che prendano in input 16 bytes
e restituiscano in output 64 bit. A sfavore di questa possibile scelta ci sono vari
fattori: uno di questi é che la tabella risultante sarebbe troppo grossa, dovrebbe
essere di 216 word da 64 bits. L’accesso a questa tabella cosı́ grossa causerebbe
problemi anche su un’architettura come Itanium dotata di una cache grande e di
una singola linea di cache L1 lunga 32 bytes. Si correrebbe il rischio di ripetuti
miss nella cache di primo livello, portando a un enorme deterioramento delle
prestazioni del codice. Altro fattore negativo che si dovrebbero usare le load8
invece che load4, e queste potrebbero causare problemi se gli accessi in memoria
non fossero allineati. Pertanto, la soluzione di utilizzare tabelle che usino in
input 8 bit e ne restituiscano 32 in output sembra quella ottimale. La istruzioni
sono state combinate in modo da sfruttare al massimo le 2 porte di load per
l’accesso alla memoria da un lato, e dall’altro le 2 unitá funzionali Integer che
eseguono le istruzioni di shift. I risultati ottenuti sono un miglioramento delle
prestazioni attorno al 30%.
7.4. RISULTATI
7.4
71
Risultati
AES-cbc 128
10485760 times on 16 size blocks
2621440 times on 64 size blocks
655360 times on 256 size blocks
163840 times on 1024 size blocks
20480 times on 8192 size blocks
Time
5. 96s
5. 24s
5. 07s
5. 02s
5. 02s
Tabella 7.3: AES-openssl speed results
type
aes-128 cbc
16 bytes
28149. 69k
64 bytes
32017. 59k
256 bytes
33091. 16k
1024 bytes
33420. 75k
8192 bytes
33420. 75k
Tabella 7.4: AES-openssl speed results
AES-cbc 128
10485760 times on 16 size blocks
2621440 times on 64 size blocks
655360 times on 256 size blocks
163840 times on 1024 size blocks
20480 times on 8192 size blocks
Time
3. 79s
3. 57s
3. 53s
3. 52s
3. 53s
Tabella 7.5: AES-optimized code speed results
type
aes-128 cbc
16 bytes
44267. 06k
64 bytes
46995. 00k
256 bytes
47527. 52k
1024 bytes
47662. 55k
8192 bytes
47527. 52k
Tabella 7.6: AES-optimized code speed results
Il codice ottimizzato impiega 3.79 secondi per compiere 10485760 volte la
funzion AES encrypt, il codice C impiega 5.96 secondi. Il miglioramento é del
36%. In realtá usando la procedura AES encrypt all’interno di openssl, il
miglioramanto é minore perché il codice assembler compilato viene poi inserito
all’interno di altro codice C, quindi la parte di codice C rallenta le prestazioni.
72
CAPITOLO 7. AES (RIJNDAEL)
Parte IV
Appendix
73
Capitolo 8
Help Itanium/OpenVMS
8.1
Assembler Itanium
Per quanto riguarda lo scrivere in assembler Itanium, ampia spiegazione é giá
stata fornita prima. Qui verrá aggiunto un esempio di codice in assembler
Itanium che potrá essere usato per iniziare.
mask1=0x00000000ffffffff
.data
.text
.global encrypt_proc
.proc encrypt_proc
encrypt_proc:
alloc loc0=ar.pfs,3,26,0,0
movl loc15=mask1
add loc16=96, in1
add loc22=64, in1;;
add in1=128, in1
br.ret.sptk.many b0
.endp encrypt_proc
Si scrive un file tipo quello sopra in cui al posto di encrypt proc c’é il nome della procedura che si vuole implementare. Una volta scritto il file assembler Itanium con qualsiasi editor disponibile, puó essere salvato con qualsiasi estensioni,
meglio .s cosı́ non ci si confonda.
8.2
Compilare il codice
Il compilatore assembler disponibile é il compilatore dell’Intel IAS. Il compilatore gcc non era in grado di compilare il codice assembler. I comandi per
compilare il codice sono semplicemente
IAS nomefile. s -o libreria.o
Il compilatore, se non ci sono errori, compiú la il file in un file output oggetto di nome libreria.o. Se in questo file c’erano riferimenti esterni a funzioni
75
76
CAPITOLO 8. HELP ITANIUM/OPENVMS
o variabili esterne, queste non vengono considerate in suddetta fase perché non
sono ancora risolte.
8.3
Linking
A questo punto si deve eseguire il linking del file C, che richiama la funzione, e
di questo file appena compilato. La soluzione é scrivere un file di header .h in
cui c’é la firma della procedura sopra implementata e includerlo nel file C. Nel
file .h troveremo una linea tipo la seguente:
void encrypt proc(int a, int b);
A questo punto si puó compiú lare il tutto e linkare con gcc. L’istruzione del tipo:
gcc libreria.o main.c -o main.exe
Da notare che é importante specificare -o main.exe perché gli eseguibili in openVMS hanno estensione exe. Se non si mette l’estensione si rischia poi di fare
confusione sul file che si vorrá eseguire.(Anche perché openVMS conserva le versioni successive dei vari file salvati). Non resta che eseguire il file compilato e
linkato.
8.4
Debugger
Ora, per vedere come funziona il codice e come stato compilato useremo il debugger di openVMS GBD. Per usare il debugger é consigliabile aggiungere al
comando gcc il flag -g che compila il file con la tabella dei nomi, in modo da
poter poi settare dei break utilizzando direttamente i nomi delle funzioni. Il
comando per poter debuggare il codice é
RUN MAIN /DEBUG
run é il comando che fa eseguire il codice, main il nome dell’eseguibile senza
estensione, /debug indica che il codice va eseguito in modalitdebugger. Una
volta eseguito il comando si entra nell’ambiente GBD. Si possono trovare online sul sito dell’HP degli ottimi manuali di GBD, oppure si puó usare l’aiuto
del debugger semplicemente digitando HELP. I comandi principali sono:
1
2
3
4
5
SET BREAK NOME FUNZIONE
-->setta un break point
alla procedura di
nome nome_funzione
GO
-->salta al prossimo break
EXAMINE NOME\_FUNZIONE:NOME\_FUNZIONE+300 -->lista a video il codice
compilato tra le linee
agli indirizzi nome_funzione
e nome\_funzione+300
STEP/INSTRUCTION 10
-->avanza di 10 istruzioni
assembler
STEP
-->avanza di una riga C
8.4. DEBUGGER
6
EXAMINE/EXADECIMAL R43
7
EXAMINE/EXADECIMAL R32:R40
8
QUIT
77
-->visualizza il contenuto del
registro r43 in esadecimale
-->visualizza i contenuti dei
registri da r32 a r4 in hex
-->esce da GBD
E’ importante mettere in maiuscolo i nomi delle funzioni nei comandi, perché
questi vengono riconosciuti solo se scritti cosı́ . Il modoficatore /EXADECIMAL
puó anche essere sostituito con /BIN ed altri. Per la scrittura di codice usando
Explicit Bundle si consulti la sezione apposita.
78
CAPITOLO 8. HELP ITANIUM/OPENVMS
Capitolo 9
Summary
The power of Itanium consists of its capabilty in executing 6 istructions simultaneously;furthermore Itanium has an efficient architecture to access to cache
and memory. Itanium also has a large number of registers and assembler istructions. The algorithms that can improve their performances in a significant way
are those which have big parallelism in the code and those which use a lot of
memory accesses. I tryed to optimized the following algorithms:
• DES
• RC5
• AES
• SHA-1
9.1
DES
Main features:
• 32 bit block is the fundamental work unitá
• permutations
• expansions
• s-boxes
• little parallelism in the code, lots of data dependences
DES has very little parallelism in the code, so DES’s performances aren’t improved very much on Itanium, because the latter doesn’t use its 6 execution
units for DES contemporaneously, it only uses one or two execution units at
the same time. As far as Expansion IP and FP are concerned it hadn’t been
possible to optimize the code over 10 %.
9.1.1
DES Results
The implemented procedure is DES encrypt. By executing this procedure 167772160
times, the optimzed code needs 8.27 seconds to be over, whereas C code ends
in 9.19 seconds.
79
80
CAPITOLO 9. SUMMARY
9.2
RC5-32/12/16
Main features:
• semplicity
• variable rotate
• use of add
• little parallelism in the code, lots of data dependences
As in the case of DES, RC5 has not a lot of parallelism in the code, so it
can’t improve its performances significantly. Furthermore RC5 uses variable
rotate and Itanium doesn’t implemnent this istruction. So RC5 improves its
performances by 10% .
rc5
20971520 times on 16 size blocks
5242880 times on 64 size blocks
1310720 times on 256 size blocks
327680 times on 1024 size blocks
40960 times on 8192 size blocks
Time
14. 6s
13. 94s
13. 76s
13. 71s
13. 7s
Tabella 9.1: RC5-openssl speed results
type
rc5
16 bytes
22982. 49k
64 bytes
24070. 61k
256 bytes
24385. 49k
1024 bytes
24474. 42k
8192 bytes
24492. 29k
Tabella 9.2: RC5-openssl speed results
rc5
20971520 times on 16 size blocks
5242880 times on 64 size blocks
1310720 times on 256 size blocks
327680 times on 1024 size blocks
40960 times on 8192 size blocks
Time
11. 08s
10. 43s
10. 24s
10. 19s
10. 18s
Tabella 9.3: RC5-optimized code speed results
type
rc5
9.3
16 bytes
44267. 06k
AES
Main features:
64 bytes
46995. 00k
256 bytes
47527. 52k
1024 bytes
47662. 55k
8192 bytes
47527. 52k
9.3. AES
81
• expansion from 128 bits to 640 bit.
• fixed rotate
• lots of parallelism in the code
• only 2 of the 5 registers used are refreshed in each round
• use of many registers for optimized performances
AES is an algorithm that strongly improves its performances on Itanium, because AES uses all the 6 execution units . AES also uses fixed rotate istruction,
and Itanium has the support for that by using the istruction shrp. Because only
2 of the 5 registers used in one round are refreshed in each round, the istructions
of one round and the istructions of the next round can be partially overlapped.
AES-cbc 128
10485760 times on 16 size blocks
2621440 times on 64 size blocks
655360 times on 256 size blocks
163840 times on 1024 size blocks
20480 times on 8192 size blocks
Time
5. 96s
5. 24s
5. 07s
5. 02s
5. 02s
Tabella 9.4: AES-openssl speed results
type
aes-128 cbc
16 bytes
28149. 69k
64 bytes
32017. 59k
256 bytes
33091. 16k
1024 bytes
33420. 75k
8192 bytes
33420. 75k
Tabella 9.5: AES-openssl speed results
AES-cbc 128
10485760 times on 16 size blocks
2621440 times on 64 size blocks
655360 times on 256 size blocks
163840 times on 1024 size blocks
20480 times on 8192 size blocks
Time
3. 79s
3. 57s
3. 53s
3. 52s
3. 53s
Tabella 9.6: AES-optimized code speed results
type
aes-128 cbc
16 bytes
44267. 06k
64 bytes
46995. 00k
256 bytes
47527. 52k
1024 bytes
47662. 55k
Tabella 9.7: AES-optimized code speed results
8192 bytes
47527. 52k
82
CAPITOLO 9. SUMMARY
9.4
SHA-1
Main features:
• optimez C code reduces the algorithm to a lots of look up in table
• works on single byte
• lots of parallelism in the code
• use of many loads from memory(table looks up)
SHA-1, in its optimized form, is reduced to many look up in table. SHA-1
improves its performances on Itanium because it has many parallelisms in the
code and it uses many loads from memory. Because Itanium can execute 2 loads
at the same time, the code is executed fast. []
SHA1 128
10485760 times on 16 size blocks
2621440 times on 64 size blocks
655360 times on 256 size blocks
163840 times on 1024 size blocks
20480 times on 8192 size blocks
Time
6. 04s
5. 96s
5. 96s
5. 94s
6. 00s
Tabella 9.8: SHA-1:openssl speed results
type
sha1 128
16 bytes
27776. 85k
64 bytes
28149. 69k
256 bytes
28149. 69k
1024 bytes
28244. 47k
8192 bytes
27962. 03k
Tabella 9.9: SHA-1:openssl speed results
SHA1 128
10485760 times on 16 size blocks
2621440 times on 64 size blocks
655360 times on 256 size blocks
163840 times on 1024 size blocks
20480 times on 8192 size blocks
Time
4. 43s
4. 42s
4. 41s
4. 40s
4. 45s
Tabella 9.10: SHA-1:optimized code speed results
type
sha1 128
16 bytes
37871. 82k
64 bytes
37957. 50k
256 bytes
38043. 57k
1024 bytes
38130. 04k
Tabella 9.11: SHA-1:optimized code speed results
8192 bytes
37701. 61k
Bibliografia
[1] Intel. 245319-Istruction Set Reference. Intel, 2002.
[2] Intel. 245318-System Archutecture Guide. Intel, 2002.
[3] Handbook of Applied Cryptography. CRC Press Inc, 1997.
[4] David C. Feldmeier. A high-speed software des implementation. Technical
report, Computer Communication Research Group Bellcore,Morriston,NJ,
1989.
[5] Intel. 245317-Application Architecture Guide. Intel, 2002.
[6] Intel. 24536301-IA-64 Assembly Language Reference Guide. Intel, 2002.
[7] Intel. 24547403-Intel Itanium Processor Reference Manual fo rSoftware
Optimization. Intel, 2002.
[8] Intel. 2511103-Intel Itanium 2 Processor Reference Manual. Intel, 2002.
[9] Intel. Intel Itanium Architecture Assembly Language Reference Guide.
Intel, 2002.
[10] Intel. asmusrgd- IA-64 Assmbler. Intel, 2002.
[11] Itanium Software Optimization Strategies.
[12] IA-64 Architecture.
[13] Paul Berreto Vincent Rijmen, Antoon Bossolaers. rijndael-alg-fst.c -fast
code for rijndael cipher. Technical report, 2000.
[14] Ronald L. Rivest. The rc5 encryption algorithm. Technical report, MIT
laboratory.
83
Scarica
Openssl - the Netgroup at Politecnico di Torino

Presentazione

Come riconoscere se il proprio PC è un 32 bit o 64 bit (Windows 7)

Openssl - the Netgroup at Politecnico di Torino

Presentazione

Come riconoscere se il proprio PC è un 32 bit o 64 bit (Windows 7)

Presentazione Rete Sincrona

Keynote Giovanni De Caro - CSI – Incubatore Napoli Est

Diapositiva 1

Presentazione - Vacanzecroate.com

Document
