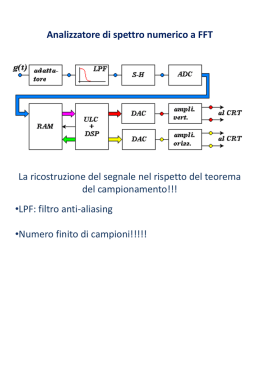
Identificazione dei sistemi:
modelli lineari e non lineari
Dai Dati alla Conoscenza
Nell’area dell’automatica il processo di identificazione ha
come obiettivo la ricerca di modelli dinamici di un sistema
(equazioni differenziali o alle differenze) che descrivono le
interazioni tra variabili di ingresso e di uscita, a partire da
dati osservati di ingresso-uscita
Sistema:
oggetto (parte di realtà) in cui variabili di differente natura
(ingressi e disturbi) interagiscono e producono effetti
osservabili (uscite)
identificazione a scatola nera:
si hanno a disposizione solo i dati I/O
le leggi che regolano i fenomeni sono sconosciute o molto complesse
la struttura del modello viene descritta generalmente da equazioni
(differenziali o alle differenze) ingresso-uscita
i parametri del modello non sono interpretabili fisicamente
identificazione a scatola grigia:
si dispone di informazioni aggiuntive
alcune parti del sistema sono modellate secondo leggi fondamentali,
altre come una scatola nera
alcuni parametri del modello possono essere interpretati fisicamente
identificazione a scatola trasparente:
(modellistica)
il sistema si può decomporre in sottosistemi di cui si conoscono le
leggi fisiche ed i parametri (unione di più modelli)
Esempio di struttura Gray-Box
Supponiamo di voler identificare un modello per le
variazioni della temperatura di una stanza al variare
della tensione applicata ad una stufa elettrica
Le leggi fisiche da considerare coinvolgerebbero le
equazioni relative alla potenza della stufa, la
trasmissione del calore per conduzione e convezione,
ecc…
Un modello Black-Box tra tensione e temperatura non dà
risultati soddisfacenti ma…
…la fisica elementare ci dice che è la potenza
della stufa piuttosto che la tensione che causa
le variazioni di temperatura!!!
un modello tra il quadrato della tensione e la
temperatura potrebbe quindi migliorare
sensibilmente le prestazioni
T (t )  a1T (t  1)a2T (t  2)  
 anT (t  n)  b1v 2 (t  1)    bm v 2 (t  m)
Classificazione dei modelli in base agli obiettivi:
•Modelli interpretativi:
Razionalizzano le informazioni disponibili sul comportamento
di un sistema sostituendo i dati con il meccanismo che li ha
generati, non è richiesta la capacità di generare altri set di dati,
hanno quindi un range di validità limitato (econometria, ecologia,
fisica).
•Modelli predittivi:
Sono sviluppati per predire il comportamento futuro del sistema
(in genere vengono utilizzati per individuare azioni di controllo)
•Modelli per la stima dello stato:
Consentono la stima di variabili interne a partire da misure I/O
affette da rumore (monitoraggio di processi naturali o industriali)
•Modelli per la diagnosi:
consentono di individuare situazioni di funzionamento anomale
(guasti nei sensori o nei componenti del processo)
•Modelli per la simulazione:
sostituiscono il sistema consentendo di valutare le prestazioni di
politiche di controllo e di valutare l’effetto di operazioni pericolose
o costose
(la possibilità di un effettivo utilizzo dipende fortemente dalla
accuratezza del modello)
A cosa serve un modello?
• Verifica immediata di ipotesi e teorie
• Predizione del comportamento futuro di un sistema
• Realizzazione di esperimenti altrimenti impossibili
• Risparmio di tempo, attrezzature, denaro
• Maggiore elasticità di progettazione
• Migliore comprensione dei fenomeni
• Correlazione tra teoria e sperimentazione
• Maggiore chiarezza nella presentazione dei risultati
• I modelli costituiscono in ogni caso una: ‘rappresentazione
abbastanza buona di alcuni aspetti del sistema’ di cui devono
essere stabiliti i limiti di validità
• Il grado di accuratezza richiesto al modello dipende dalla sua
applicazione
• Il grado di accuratezza è limitato anche dal grado di complessità
tollerabile, dal tempo a disposizione per sviluppare il modello, dalle
informazioni contenute nei dati, dalle conoscenze a priori, dal grado di
nonlinearità, dalla possibilità di effettuare esperimenti, dal costo delle
misure, dalla precisione dei sensori, dal rumore di misura
Rasoio di Occam (1300): tra i modelli che descrivono lo stesso
fenomeno si deve scegliere il modello più semplice
Popper (1900): tra i modelli che rappresentano le osservazioni
disponibili si deve scegliere quello che consente di spiegare ‘as little
else is possible’ (most powerful unfalsified model)
dim. matematica: se il modello è ricavato da dati incerti,
all’aumentare della complessità del modello aumenta l’incertezza sui
suoi parametri
Ipotesi:
Sistema tempo invariante a parametri concentrati
Modelli lineari o non lineari?
Tutti i sistemi reali sono, in misura più o meno accentuata, non lineari
Se sono rispettate alcune condizioni :
- variazioni delle grandezze piccole rispetto al punto di lavoro nominale
- è sufficiente avere un modello approssimato del sistema
- è possibile ricorrere ad una approssimazione lineare del sistema, ricorrendo
eventualmente a modelli diversi nei diversi punti di lavoro
in questo caso:
la teoria è in grado di prevedere le prestazioni del modello
le procedure numeriche sono più semplici
il progetto di un eventuale sistema di controllo è facilitato
Qualora tali approssimazioni non siano lecite è necessario ricorrere a strutture non lineari
(Quale struttura?)
ingredienti
• dati sperimentali
• insieme di modelli candidati
(scelti utilizzando tutte le informazioni a priori disponibili: ordine del
sistema, dinamiche lente o veloci, stabilità, presenza di ritardi,
frequenza di campionamento, grado e tipo di non linearità)
• regola con la quale determinare il modello nella classe
dei candidati sfruttando le informazioni contenute nei dati
• criterio per la valutazione della qualità del modello
ottenuto
Le Fasi del Processo di Identificazione
Conoscenza A Priori
Progetto
degli
Esperimenti
Ottenimento ed
Preprocessamento
dei Dati Sperimentali
Selezione della
Struttura del
Modello
Selezione del
Criterio
Stima del Modello
Not OK
Validazione del Modello
OK
(L. Ljung, 1999)
Cause di fallimento
• la procedura numerica non ha trovato il modello migliore
tra i candidati secondo il criterio scelto
(minimi locali nelle procedure di ottimizzazione,
malcondizionamento)
• il criterio non è adeguato
• la classe dei modelli non è adeguata
• i dati non contengono abbastanza informazioni (pochi
esperimenti, troppo rumore)
Scelta delle variabili di ingresso
Si può fare in base a:
Conoscenze sulla fisica del processo
Conoscenze empiriche degli operatori
Indici di correlazione
Trial and error
Scelta dei dati ed esperimenti
Lo scopo degli esperimenti è quello di collezionare dati in
grado di rappresentare l’intera dinamica del sistema
I modelli ottenuti non possono fornire più informazioni di
quante non ne siano contenute nei dati!!!
Progetto degli Esperimenti
Selezione del tipo di ingressi con i quali si ecciterà il
sistema. Devono essere sufficientemente ricchi al fine di
sollecitare tutti i modi del sistema (persistenza
dell’eccitazione)
Solo i modi osservabili e controllabili del sistema possono
essere identificati
Tipi comuni di ingressi: rumore bianco, pseudo-random
binary sequence, treni di gradini/impulsi, sinusoidi, forme
tipiche relative al processo in esame
Scelta del tempo di campionamento
•
I segnali (di ingresso e di uscita di un processo) possono essere
pensati come la sovrapposizione di segnali elementari (sinusoidi).
• ‘L’insieme’ di tali sinusoidi costituisce lo ’spettro del segnale’’
(determinabile utilizzando opportuni strumenti: analizzatore di spettro).
onda quadra
spettro
Lo spettro del segnale di uscita di un sistema dipende dal
corrispondente spettro del segnale in ingresso e dalle ‘proprietà
filtranti’ del sistema
Tutti i sistemi reali possono generare in uscita segnali che non si
estendono oltre una certa frequenza massima (banda passante del
sistema)
Teorema del campionamento
Se si campiona un segnale a frequenza almeno doppia rispetto alla
massima frequenza contenuta nel segnale, è possibile ricostruire,
senza perdita di informazione in segnale originale
se il teorema non viene rispettato si può incorrere in problemi di
aliasing e non è possibile ricostruire il segnale originario
partendo dai dati campionati
Sinusoide
campionata
a diverse
frequenze
Non rispetta
il teorema
di Shannon
Lo spettro di un segnale campionato è costituito da repliche dello
spettro del segnale originario, che si ripetono a un intervallo di
frequenza costante e pari alla frequenza di campionamento.
Se non è rispettato il teorema di Shannon tali repliche si
sovrappongono (Aliasing) e non è possibile risalire, a seguito di una
operazione di filtraggio allo spettro del segnale originario.
Frequenza di campionamento
Spettro del segnale
Campionamento
Frequenza di campionamento
Spettro del segnale
Spettro del segnale campionato
Campionamento
Spettro del segnale campionato
Altri criteri per la scelta del tempo di campionamento
Il segnale campionato deve rappresentare la dinamica del sistema
T=0.01
100 campioni
T=0.1
10 campioni
T=0.05 =ts/6
20 campioni
Sistema di primo ordine
Polo: -10
Costante di tempo
1/10=0.1
Tempo di salita 3* 0.1
T=0.1
80 campioni
T=0.2 =ts/5
40 campioni
Sistema del secondo ordine
T=1
8 campioni
ts=1 sec
ta=5 sec
Sistema del quarto ordine
T=0.1 sec
T=1 sec
T=0.2 sec=ts/6
T=4 sec
Criteri generali :
ts/5 < T < ts/10
ta/10 < T < ta/50
T < della più piccola costante di tempo
f=1/T > 2* fmax
Se T è troppo piccolo:
• occorre manipolare un numero eccessivo di dati
senza migliorare l’informazione che contengono
• si rischia di campionare il rumore
• dati troppo simili tra loro creano problemi numerici agli algoritmi
• il tempo di elaborazione aumenta
•Il costo di acquisizione aumenta
Come è possibile verificare se è stato rispettato
il Teorema del Campionamento?
• Se si hanno dubbi sulla correttezza del campionamento, si può calcolare
lo spettro del segnale campionato:
Se questo mantiene valori elevati a tutte le frequenze (nel discreto le
frequenze vanno da zero a 0.5 volte la frequenza di campionamento) è
ragionevole supporre che sia stata scelta una frequenza di
campionamento troppo bassa.
Se la banda occupata dallo spettro è una frazione piccola
dell’intervallo a disposizione è stata utilizzata una frequenza di
campionamento inutilmente elevata.
Può essere opportuno in tale caso procedere ad un filtraggio digitale
dei dati. Ciò permette di risparmiare risorse e elimina rumore (di
misura) a frequenze elevate.
Adeguatezza del Tempo di Campionamento
6
6
5.5
5.5
5
5
4.5
4.5
4
4
3.5
3.5
3
20
40
60
80
100
120
140
160
180
200
3
5
10
15
20
25
30
35
40
45
50
60
180
160
50
140
120
40
100
30
80
60
20
40
10
20
0
0
100
200
300
400
500
600
Tc adeguato
700
800
900
1000
0
0
50
100
150
200
250
Tc troppo grande
300
350