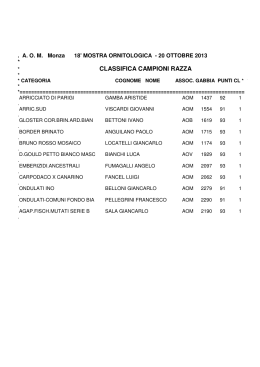
Teoria del
calcestruzzo armato
LIVELLI DI ANALISI
Sono possibili i seguenti livelli di analisi per le strutture in calcestruzzo armato:
I stadio:
• comportamento elastico lineare di calcestruzzo e acciaio;
• calcestruzzo
l
reagente a trazione.
i
II stadio:
• comportamento elastico lineare di calcestruzzo e acciaio;
• calcestruzzo non reagente a trazione.
III stadio:
• comportamento non lineare di calcestruzzo e acciaio;
• calcestruzzo non reagente a trazione.
AZIONE ASSIALE
Comportamento al I-II stadio di un elemento in calcestruzzo armato soggetto a sola
azione assiale N
Ipotesi per il dimensionamento del pilastro in c.a.:
1. Il calcestruzzo è un materiale omogeneo ed isotropo, con comportamento
elastico e lineare. Il suo modulo di elasticità (o modulo di Young) dipende dalla
composizione e risulta circa EC = 300000 kg/cm2.
2 Il modulo di elasticità dell
2.
dell’acciaio
acciaio è ES=2050000 kg/ cm2.
3. I due materiali utilizzati, pur avendo un differente modulo di elasticità, hanno la
medesima deformazione, a causa della perfetta adesione.
4. le sezioni trasversali rimangono piane anche dopo essere state deformate.
N
L’azione assiale di compressione N si ripartisce fra acciaio e calcestruzzo:
N = Ns + Nc.
Ricordando che: tensione × area = forza:
σ × A = F,
si ottiene che:
(σS⋅ AS) + (σC ⋅ AC) = N. (equilibrio)
Il pilastro sottoposto ad una forza di compressione N tende a deformarsi.
deformarsi
La deformazione ε sarà uguale sia per il calcestruzzo che per l’acciaio.
Pertanto:
ε = εC = εS = δ/l,
(congruenza)
dove δ è lo spostamento e l è la lunghezza iniziale della barra.
barra
Ricordando il legame costitutivo:
σC
εC =
,
EC
σ
εS = S .
ES
Si ottiene:
σC σS
=
,
EC ES
ES
σS =
⋅ σC .
EC
Il rapporto fra i moduli è il coefficiente di omogeneizzazione e viene
indicato con la lettera n.
Q
Quindi
sostituendo nella equazione
q
di equilibro
q
alla traslazione
verticale, si ottiene:
(n σC AS) + (σC AC) = N,
da cui:
N
.
σC =
n ⋅ AS + AC
Il valore del coefficiente di omogeneizzazione che si assume è n=15.
E’ doveroso chiedersi perché sia stato attribuito questo valore a n;
considerando che n è il rapporto tra i moduli di elasticità dei due materiali, il
suo valore dovrebbe essere:
E S 2050000
n=
=
≅7
EC
300000
La motivazione è che i moduli di elasticità sono misurati in laboratorio
istantaneamente, mentre gli edifici sono caricati con carichi prolungati nel
tempo. Il comportamento dei due materiali sottoposti a carichi di lunga durata
è molto
lt diverso:
di
mentre
t l’acciaio
l’ i i sii deforma
d f
e poii sii stabilizza,
t bili
il calcestruzzo
l t
evidenzia deformazioni differite.
Questo fenomeno per il calcestruzzo viene denominato viscosità e giustifica
un valore più elevato del coefficiente n. Per viscosità la deformazione nel cl
cresce nel tempo a sforzo costante, quindi anche la deformazione dell’acciaio
cresce e con essa lo sforzo nell
nell’acciaio;
acciaio; quindi con n=15 colgo la situazione
dopo lungo tempo.
Esempio: si consideri un pilastro di sezione trasversale quadrata, soggetto a
carico concentrato N di compressione.
compressione
I dati sono:
• N = 800 kN
• Lato pilastro = 35 cm
Si ipotizzi
i i i allora
ll
l’ ili
l’utilizzo
di quattro ferri
f i di diametro
di
φ = 12 mm; se ne
calcoli l’area totale e si confronti questo risultato con l’area del pilastro:
Abarre = nbarre ⋅ Abarra
⎛ 1,2 2 ⎞
⎟⎟ = 4.52 cm 2
= 4 ⋅ ⎜⎜ π ⋅
4 ⎠
⎝
Abarre 4.52
=
= 0.0037
AP
1225
La normativa prevede che la superficie delle sezioni trasversali delle barre sia:
0.003Ap < area barre < 0.06Ap
Ora si sostituiscano tutti i valori noti nella formula di verifica: si otterrà così il
valore dello sforzo cui è sottoposto il calcestruzzo.
calcestruzzo
Con N = 800 kN, n=15, Abarre= 4.52 cm2, AP= 1225 cm2, si ottiene:
σc = 6.2
6 2 MPa.
MP
LA FLESSIONE SEMPLICE
Comportamento al I e II stadio di un elemento in calcestruzzo armato soggetto a solo
momento flettente M (caso di flessione retta).
Si consideri una sezione, la cui altezza sia h e larghezza b, i cui ferri d’armatura di
area As (in zona tesa) e A′s (in zona compressa) distino dai bordi superiore ed inferiore
di una distanza c.
b
εc
σc
σ s′
ε′s
A′s
h
As
εs
σs
εt
σt
x
Ipotesi di comportamento al primo stadio:
1.
Le sezioni possono ruotare, ma rimangono piane (ipotesi di Navier);
2.
Perfetta aderenza tra calcestruzzo e acciaio sia in zona compressa che in zona tesa.
3.
Il calcestruzzo è omogeneo, isotropo, con comportamento elastico-lineare sia a
compressione che a trazione;
4.
L’acciaio è omogeneo, isotropo, con comportamento elastico e lineare;
b
εc
σc
σ s′ / n
ε′s
h
εs
σs/n
εt
σt
x
Per le ipotesi 1) e 2) posso scrivere (congruenza):
εc
x
εc
x
=
=
ε s′
x−c
εs
h−c− x
εc
x
=
εt
h−x
→
x−c
ε s′ =
εc
x
→
εs =
→
h−x
εt =
εc
x
h−c− x
εc
x
Per le ipotesi 3) e 4) posso scrivere (leg. costitutivo):
⎧σ c = Ecε c
⎪σ = E ε
⎪ t
c t
⎨
⎪σ s = Esε s
⎪⎩σ s′ = Esε s′
Segue che:
σ s′
Es
=
E x−c
x − c σc
x−c
→ σ s′ = s
σ c → σ s′ = n
σc
x Ec
Ec x
x
σs
Es h − c − x
h −c − x σc
h−c− x
σc → σs = n
σc
=
→ σs =
Es
x
Ec
Ec
x
x
σt
Ec
=
h − x σc
h−x
→ σt =
σc
x Ec
x
Impongo l’equilibrio orizzontale (Nint=0):
x
h−x
′
′
− σ c b − σ s As + σ s As + σ t
b=0
2
2
Sostituisco quanto trovato prima:
x
x−c
h−c− x
h−x h−x
′
−σc b − n
σ c As + n
σ c As +
σc
b=0
2
x
x
2
x
Da cui:
x
x−c
h−c− x h− x h− x
− b − nAs′
+ nAs
+
b=0
2
x
x
x
2
2
(
x2
h − x)
− b − nAs′ ( x − c ) + nAs (h − x − c ) +
b=0 → x
2
2
NB. La posizione dell’asse neutro è quella tale da annullare rispetto ad essa il momento
statico della sezione omogenizzata (calcestruzzo teso e compresso più area di acciaio
moltiplicata per il coefficiente n) cioè coincide con il baricentro della sezione
omogenizzata.
(
x2
h − x)
− b − nAs′ ( x − c ) + nAs (h − x − c ) +
b=0
2
2
x2
h2
x2
− b − nAs′ x + nAs′c + nAs (h − c ) − nAs x + b + b − hbx = 0
123
2
2
2
d
h2
b + nAs′c + nAs d
S om
2
x=
=
nAs′ + nAs + hb
Aom
2
Impongo l’equilibrio alla rotazione orizzontale rispetto all’asse neutro (Mint=M):
x ⎛2 ⎞
2 ⎝3 ⎠
σ c b⎜ x ⎟ + σ s′ As′ (x − c ) + σ s As (h − c − x ) + σ t
h−x 2
b (h − x ) = M
2
3
Sostituisco quanto trovato prima:
x ⎛2 ⎞
2 ⎝3 ⎠
x−c
h−c− x
σ c As′ (x − c ) + n
σ c As (h − c − x ) +
x
x
h−x h−x 2
+
σc
b (h − x ) = M
x
2
3
σ c b⎜ x ⎟ + n
Da cui:
3
⎡ x3
⎤
(
)
h
−
x
2
2
′
σ c ⎢ b + nAs ( x − c ) + nAs (h − c − x ) +
b ⎥ = Mx
⎣13444444444244444443443⎦
J om
Da cui:
M
σc =
x
J om
Sostituisco in quanto trovato prima:
σ s′ = n
M
(x − c )
J om
σs = n
M
(h − c − x )
J om
M
(h − x )
σt =
J om
All’aumentare del carico questa soluzione perde di validità in quanto il calcestruzzo,
avente scarsa resistenza a trazione si fessura.
p
della resistenza a trazione del calcestruzzo NON comporta
p
comunque
q il
Il superamento
collasso della sezione.
Ipotesi di comportamento al secondo stadio:
1.
Le sezioni possono ruotare, ma rimangono piane (ipotesi di Navier);
2.
Perfetta aderenza tra calcestruzzo e acciaio sia in zona compressa che in zona tesa.
3.
Il calcestruzzo è omogeneo, isotropo, con comportamento elastico-lineare a
compressione mentre non resiste a trazione (σt=0);
4.
L’acciaio è omogeneo, isotropo, con comportamento elastico e lineare;
b
εc
σc
σ s′
ε′s
h
εs
σs
εt
σt
x
Per le ipotesi 1) e 2) posso scrivere (congruenza):
εc
x
εc
x
=
=
ε s′
x−c
εs
h−c− x
→
x−c
ε s′ =
εc
x
→
εs =
h−c− x
εc
x
Per le ipotesi 3) e 4) posso scrivere (leg. costitutivo):
⎧σ c = Ecε c
⎪σ = E ε
⎪ s
s s
⎨
⎪σ s′ = Esε s′
⎪⎩σ t = 0
Segue che:
σ s′
Es x − c
x − c σc
x−c
′
′
=
→ σs =
σc → σs = n
σc
Es
x Ec
Ec x
x
σs
Es
=
E h−c− x
h − c − x σc
h−c− x
→ σs = s
σc → σs = n
σc
Ec
x
x
Ec
x
Impongo l’equilibrio orizzontale (Nint=0):
x
− σ c b − σ s′ As′ + σ s As = 0
2
Sostituisco quanto trovato prima:
x
x−c
h−c− x
′
−σc b − n
σ c As + n
σ c As = 0
2
x
x
Da cui:
x
x−c
h−c− x
− b − nAs′
+ nAs
=0
2
x
x
x2
− b − nAs′ ( x − c ) + nAs (h − x − c ) = 0 → x
2
NB. La p
posizione dell’asse neutro è q
quella tale da annullare rispetto
p
ad essa il momento
statico della sezione omogenizzata e parzializzata (calcestruzzo compresso più area di
acciaio moltiplicata per il coefficiente n)
Impongo l’equilibrio alla rotazione rispetto all’asse neutro (Mint=M):
x ⎛2 ⎞
2 ⎝3 ⎠
σ c b⎜ x ⎟ + σ s′ As′ (x − c ) + σ s As (h − c − x ) = M
Sostituisco quanto trovato prima:
x ⎛2 ⎞
x−c
h−c− x
σ c b⎜ x ⎟ + n
σ c As′ (x − c ) + n
σ c As (h − c − x ) = M
2 ⎝3 ⎠
x
x
Da cui:
⎡ x3
2
2⎤
′
σ c ⎢ b + nAs (x − c ) + nAs (h − c − x ) ⎥ = Mx
⎣1344444424444443⎦
J om
Da cui:
σc =
M
x
J om
Sostituisco in quanto trovato prima:
σ s′ = n
M
(x − c )
J om
M
M
(h − c − x ) = n (d − x )
σs = n
J om
J om
dove d = h - c è detta altezza utile della sezione
Nella flessione semplice il momento flettente agente viene quindi equilibrato
con una coppia interna formata dalla risultante degli sforzi di compressione
agenti nel calcestruzzo e nell’armatura compressa e dagli sforzi di trazione
agenti nella sola armatura tesa.
Sezione a T
Sono possibili due casi:
1. x<s: l’asse neutro taglia la soletta e la sezione si comporta come
rettangolare con b=bs;
2. x>s: le ali sono equivalenti ad un’area di acciaio Ase= (bs- b) s/n e c’=s/2;
la sezione si assume rettangolare con base uguale a b.
Ase
bs
x
s
xc
d
b
LA (TENSO) - PRESSO-FLESSIONE
Comportamento al II stadio di un elemento in calcestruzzo
armato soggetto Ad azione assiale combinata con momento
flettente M.
La condizione di sollecitazione più generale che produce
tensioni normali nei pilastri dei telai è la combinazione di
azione normale e flessione.
Lo stato di sollecitazione viene individuato dalla forza normale
N e dal ppunto P di coordinate xp yp, detto centro di
sollecitazione, intersezione della retta di azione di N con il
piano della sezione. In alternativa la stessa sollecitazione può
descriversi mediante N ed i due momenti baricentrici Mx, My
relativi agli assi principali di inerzia della sezione.
Nel seguito, nella parte dedicata al calcolo elastico, si farà di
solito riferimento agli assi principali dell
intera sezione
dell’intera
omogenizzata, che sono, quando la sezione è interamente
compressa, gli assi principali della sezione reagente.
Generalmente questi
q esti assi coincidono,
coincidono o differiscono di poco,
poco
dagli assi della sezione geometrica.
N
Mx
My
N
Piccola Eccentricità
Si considera il caso che l’azione normale sia di compressione; se, con
riferimento alla sezione omogenizzata, il centro di sollecitazione è interno al
nocciolo centrale di inerzia,
inerzia ll’asse
asse neutro è esterno alla sezione che pertanto
risulta interamente compressa e dunque reagente. In questo caso le
caratteristiche geometriche della sezione sono note a priori e per calcolare lo
stato di tensione si possono utilizzare
tili are le relazioni
rela ioni che si ottengono applicando la
sovrapposizione degli effetti, ben note dallo studio delle travi. Sempre con
riferimento agli assi principali di inerzia, la tensione in un generico punto della
sezione,
i
di coordinate
di
x, y è data
d dall’equazione:
d ll’
i
Nx p
Ny p
N
N
Ne
σc =
+
x+
y=
+
y
Aom I yom
I xom
Aom I xom
in cui xp, yp sono le coordinate del centro di sollecitazione e Ix, Iy i momenti
d’inerzia della sezione omogenizzata.
Grande eccentricità - Pressoflessione retta
Quando il centro di sollecitazione è esterno al nocciolo l’asse neutro taglia la
sezione che risulta parzializzata e, come nel caso della flessione, la sezione
reagente nel II stadio non è a priori determinata.
determinata
Se la sezione ha un asse di simmetria ed il centro di sollecitazione è uno dei
suoi punti l’asse neutro è ortogonale a questo asse, e la sua giacitura dunque è
nota; questo,
q esto come già fu
f visto
isto per la flessione,
flessione semplifica il problema che
tuttavia si può trattare in forma analitica solo per sezioni dalla geometria
semplice. Anche qui il caso più elementare e di maggior interesse pratico è
quello
ll delle
d ll sezioni
i i rettangolari.
l i
Se y è l’asse di simmetria su cui giace il centro di sollecitazione P, si indichi
con u la distanza di P dal bordo compresso della sezione, considerata positiva
quando P è esterno alla sezione, con yp la distanza (incognita) di P dall’asse
neutro e con yc l’altezza (incognita) della zona compressa si ha:
y p = yc + u
Con riferimento all’asse x perpendicolare ad y e passante per P, la condizione di
equilibrio alla rotazione della sezione richiede che:
∫
Aom
σy′dA = 0
dove y’ indica la distanza di un
punto generico della sezione
dall’asse x’. Se y è la distanza
distan a
dello stesso punto dall’asse
neutro, si avrà ovviamente
y = yp − y’
Tenendo presente che, per la
linearità del diagramma delle
tensioni,, si p
può p
porre:
σ = ky=k(yp − y’)
dalla equazione precedente si
ottiene:
yp ∫
Aom
y′dA − ∫
Aom
y′2 dA = 0
y’
che, sinteticamente, si può scrivere:
yp Sx’ − Ix’ = 0
in cui Sx’ e Ix’ sono il momento statico e quello d’inerzia della sezione
reagente omogenizzata, riferiti all’asse x’.
Sezione rettangolare
Per una sezione rettangolare
g
l’espressione
p
esplicita
p
di Sxx’ e Ixx’ è semplice:
p
(
)
(
)
1
S x′ = b y 2p − u 2 + nAs′ (d ′ + u ) + nAs (d + u )
2
1
2
2
I x′ = b y 3p − u 3 + nAs′ (d ′ + u ) + nA
As (d + u )
3
Sostituendo queste espressioni e riordinando i termini in funzione dell’unica
incognita yp che vi compare, si ottiene l’equazione cubica:
⎡ 6n
⎤
y + ⎢ [As′ (d ′ + u ) + As (d + u )] − 3u 2 ⎥ y p −
⎣b
⎦
⎡ 6n
2
2
3⎤
′
′
+⎢
As (d + u ) + As (d + u ) − 2u ⎥ = 0
⎣b
⎦
3
p
[
]
che si può scrivere in modo compatto:
yp3 + ypp − q = 0
ddove i coefficienti
ffi i ti p e q dipendono
di d
dalla
d ll geometria
t i della
d ll sezione,
i
dalle
d ll armature
t
e
dalla posizione del centro di sollecitazione.
La soluzione dell’equazione cubica è nota in forma esplicita:
Specificatamente al caso di sezione con un solo strato di armatura a trazione e a
compressione, l’equilibrio alla rotazione attorno al punto P, implica che:
σc
y
y’
y
σ = ky
k
σ c yc ⎛
σ c yc
yc ⎞
b⎜ u + ⎟ + σ s′ As′ (d ′ + u ) − σ s As (d + u ) = 0
2 ⎝
3⎠
σ s′
σs
-
}
64
4744
8
64748
ky c2 ⎛
yc ⎞
b ⎜ u + ⎟ + nk ( y c − d ′ ) As′ ( u + d ′ ) + nk ( d − y c ) As ( u + d ) = 0
2
3 ⎠
⎝
σ c yc
}
σ s′
σs
64
4744
8
64748
ky c2 ⎛
yc ⎞
b ⎜ u + ⎟ + nk ( y c − d ′ ) As′ ( u + d ′ ) +- nk ( d − y c ) As ( u + d ) = 0
2
3 ⎠
⎝
6n
y + 3uy + [As′ (d ′ + u ) + As (d + u )]yc −
b
6n
+ [d ′As′ (d ′ + u ) + dAs (d + u )] = 0
b
3
c
2
c
Da cui ricavare la posizione dell’asse neutro
yc
Dal valore di yp si determina quindi l’altezza della zona compressa yc = yp −
u Individuata la posizione dell
u.
dell’asse
asse neutro la sezione reagente risulta definita
e quindi si può procedere al calcolo delle sollecitazioni. Risulta comodo
utilizzare l’equazione monomia che si ricava dall’equilibrio alla traslazione:
∫ σdA = k ∫
Aom
Aom
ydA = kSom = N → k =
N
S om
σ c yc
σ s′
σs
}
64
4
744
8
64
4
744
8
2
k yc
b + n k ( y c − d ′ ) As′ − n k ( d − y c ) As = N
2
in cui si è fatto uso della relazione lineare σ = ky e si è indicato con Som il
momento statico della sezione
se ione omogenizzata
omogeni ata relativamente
relati amente all’asse neutro.
ne tro
Risolvendo ll’equazione
equazione rispetto a k e sostituendo la soluzione nella espressione di
σ = ky si ha:
σc =
N
y
S om
I valori delle tensioni nell’acciaio si ottengono con una relazione analoga
amplificata del fattore n:
N
σ s′ = n
( yc − d ′ )
Som
σs = n
N
( d − yc )
Som
u
-