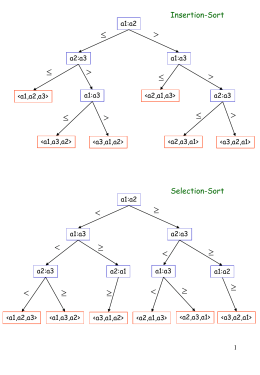
a1:a2

Insertion-Sort

a2:a3
a1:a3


a1:a3
<a1,a2,a3>
<a2,a1,a3>
<a1,a3,a2>
<a2,a3,a1>
<a3,a1,a2>


a2:a3

a2:a3
<a3,a2,a1>
Selection-Sort
a1:a3



a1:a2
<a1,a2,a3>
a2:a3







a2:a1
a1:a3



<a1,a3,a2>
<a3,a1,a2>
<a2,a1,a3>
a1:a2

<a2,a3,a1>

<a3,a2,a1>
1
Esercizio 2
Consideriamo una funzione f(n) tale che:
f(n) = (n log2(n))
La relazione precedente implica anche:
f(n) = (n logB(n))
B = base generica
----------------------------------------Infatti:
f(n) = (n log2(n))   c, n0 > 0 tali che  n  n0
0  c n log2(n)  f(n)
Notiamo che:
log2(n) = logB(n) / logB(2)
Posso definire c’ = c / logB(2). Vale allora la relazione:
n  n0
Da cui segue:
0  c’ n logB(n)  f(n)
f(n) = (n logB(n))
2
Esercizio – Fusione di due sequenze ordinate
Considerare il problema della fusione di 2 sequenze
ordinate di lunghezza n/2 in una sequenza ordinata di
lunghezza n. Scrivere un algoritmo, analizzarne la
complessità, valutare se l’algoritmo scritto è un
algoritmo ottimale.
Alcune domande preliminari:
- Lower bound ? Boh…quello banale è pari ad Ω(n)
- Upper bound ? Vediamo…parto con un algoritmo banale
Merge1(A,B)
For i 1 to n/2
do C[i]  A[i]
C[n/2+i]  B[i]
Insertion-Sort(C)
-L’algoritmo è corretto?
SI
- Complessità temporale e spaziale dell’algoritmo?
O(n2), come l’Insertion Sort
- L’algoritmo è ottimale?

Direi di NO…
3
Un altro algoritmo di fusione…
Merge2(A,B)
i 1
j1
While (i  n/2) and (j  n/2)
do if (A[i] < B[j])
then C[i+j-1]  A[i]
ii+1
else C[i+j-1]  B[j]
jj+1
If (i > n/2)
then for k  j to n/2
do C[k+n/2]  B[k]
else for k  i to n/2
do C[k+n/2]  A[k]
-L’algoritmo è corretto?
SI
- Complessità temporale e spaziale dell’algoritmo?
O(n)
- L’algoritmo è ottimale?
 SI!!
4
Algoritmi di ordinamento ottimali
Problema dell’ ordinamento per confronto:
Lower bound - (n log(n))
considerazioni teoriche
Upper bound – O(n2)
IS,SS
Proviamo a costruire un algoritmo ottimale.
Notiamo che:
IS e SS utilizzano un approccio incrementale
alla k-esima iterazione essi producono una sequenza
ordinata di k elementi
5
L’ approccio incrementale non è l’unico approccio possibile:
Approccio divide-et-impera (divide-and-conquer)
- Il problema è diviso in un certo numero di sottoproblemi (divide)
-I sottoproblemi vengono risolti separatamente (impera);
- Le soluzioni dei sottoproblemi vengono combinate per
ottenere la soluzione del problema iniziale (combina).
6
Algoritmo Merge-Sort
Merge-Sort(A, p, r)
If (p < r)
then q = (p+r)/2 
Merge-Sort(A, p,q)
Merge-Sort(A, q+1, r)
Merge(A, p, q, r)
Merge(A, p, q, r)
Assume che:
A[p …… q] ordinata
A[q+1 …… r] ordinata
Genera:
A[p …… r] ordinata
Per ordinare A si lancia Merge-Sort(A,1,n)
Funzionamento del Merge-Sort per n=8: valore dei
parametri p,r
p,r
Merge-Sort
1,8
1,4
1,2
1,1
2,2
5,8
3,4
3,3
5,6
4,4
5,5
7,8
6,6
7,7
8,8
7
Funzionamento del Merge-Sort: progressione delle
chiamate ricorsive
p1 =1
r1 =8
q1 =4
Merge-Sort
p2 =1
r2 =4
q2 =2
p3 =1
r3 =2
q3 =1
p4 =1
r4 =1
q4 =
p4 =2
r4 =2
q4 =
p2 =5
r2 =8
q2 =6
p3 =5
r3 =6
q3 =5
p3 =3
r3 =4
q3 =3
p4 =3
r4 =3
q4 =
p4 =4
r4 =4
q4 =
p4 =5
r4 =5
q4 =
p3 =7
r3 =8
q3 =7
p4 =6
r4 =6
q4 =
p4 =7
r4 =7
q4 =
p4 =8
r4 =8
q4 =
8
Funzionamento del Merge-Sort: un esempio
n =8
A = < 5,2,4,6,1,3,8,7 >
5,2,4,6,1,3,8,7
Merge-Sort
1,2,3,4,5,6,7,8
5,2,4,6
1,3,8,7
2,4,5,6
5,2
4,6
2
1,3
4,6
2,5
5
1,3,7,8
4
6
8,7
1,3
1
3
7,8
8
7
9
Complessità temporale del Merge Sort
Merge-Sort(A, p, r)
If (p < r)
then q = (p+r)/2 
Merge-Sort(A, p,q)
Merge-Sort(A, q+1, r)
Merge(A, p, q, r)
Ci aspettiamo che il comportamento asintotico del MergeSort sia migliore del comportamento asintotico di IS e
SS. Infatti, l’approccio ricorsivo dovrebbe aggirare i
problemi indotti dall’approccio incrementale.
10
Complessità temporale del Merge-Sort
Merge-Sort(A, p, r)
If (p < r)
then q = (p+r)/2 
Merge-Sort(A, p,q)
Merge-Sort(A, q+1, r)
Merge(A, p, q, r)
Il Merge-Sort è un algoritmo ricorsivo 
Il tempo di esecuzione del MS verifica un equazione di
ricorrenza
Tms(n) = d(n) + 2*Tms(n/2) + c(n)
d(n)  tempo necessario a dividere in
 (1)
2 sequenze lunghe n/2
c(n)  tempo necessario per combinare
 (n)
2 sequenze ordinate di n/2 elementi (Merge())
Tms(n) = 2 *Tms(n/2) + f(n)
f(n) = d(n) + c(n) = (n)
Questa equazione vale per tutti i valori di n eccetto che per
n=1:
Notare: Se conoscessi Tms(n/2), potrei determinare Tms(n).
11
Teorema principale
Siano a, b,c costanti non negative. La soluzione dell’
equazione di ricorrenza:
T(n) =
b
aT(n/c) + b n
per n = 1
per n > 1
è:
Θ(n)
T(n)= Θ(n log n)
Θ(n logca)
se a < c
se a = c
se a > c
12
Nel caso del Merge-Sort, a=b=2
 La complessità temporale dell’algoritmo Merge-Sort
è:
T(n) = (nlogn)
 Ciò implica che l’algoritmo Merge-Sort è un
algoritmo di ordinamento ottimale!!
13