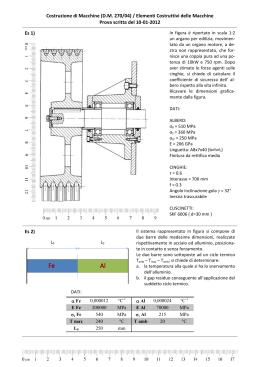
Si riporta di seguito la risoluzione di alcuni esercizi riguardanti il calcolo del momento resistente e
del dominio di pressoflessione di sezioni in cemento armato. In tutte le applicazioni successive si è
utilizzato per il calcestruzzo il legame rettangolo (stress block).
Esempio 1
Si consideri la sezione di un solaio latero-cementizio (1 m) di caratteristiche geometriche:
-
altezza geometrica h = 240 mm;
copriferro c = 40 mm;
altezza utile d = 200 mm;
interasse travetti i = 500 mm;
spessore travetti t = 100 mm;
altezza soletta s = 40 mm;
Sono impiegati un calcestruzzo di classe 25/30, caratterizzato da:
-
fck = 25 MPa; σ cd =
0,85 ⋅ 25
= 14,17 MPa
1,5
ed un acciaio B450C, caratterizzato da
-
fyk = 450 MPa; f yd =
455
= 391,3 MPa ; Es = 210 000 MPa.
1,15
Si procede al calcolo del valore del momento resistente in campata (momento positivo) supponendo
un armatura inferiore (per singolo travetto): As = 2 φ 12 mm = 226 mm2.
Nel caso di sezione a T, l’asse neutro può avere profondità tale da essere interno alla soletta o
interno all’anima della sezione. Si ipotizza in prima istanza che l’asse neutro sia interno alla soletta;
in tale caso la sezione a T può essere trattata come una sezione rettangolare di dimensioni
b=1000mm h=240mm (salvo poi verificare che l’asse neutro sia interno alla soletta di spessore
s=40mm). In tale ipotesi si ha:
ω=
As f yd
bhσ cd
=
2 ⋅ 226 ⋅ 391,3
= 0,0520 ⇒ y = h ⋅ ω = 240 ⋅ 0,0520 = 12,48 mm
1000 ⋅ 240 ⋅ 14,17
e quindi la profondità dell’asse neutro vale
x = 1.25 y = 15,6 mm < s
dunque l’asse neutro taglia la soletta e l’ipotesi assunta risulta valida. Il braccio della coppia interna
vale pertanto:
d * = d − 0,5 y = 200 − 0,5 ⋅ 12,48 = 193,76 mm
e quindi il momento resistente di progetto vale:
M Rd = T ⋅ d * = As f yd (d − 0,5 y ) = 226 ⋅ 391,3 ⋅ 193,76 = 17,13 ⋅ 10 6 Nmm (= 17,1 kNm)
Esempio 2
Si consideri una sezione in cemento armato di caratteristiche geometriche:
-
base b = 400 mm;
altezza geometrica h = 500 mm;
altezza utile d = 460 mm;
copriferro c = 40 mm;
armatura in trazione As = 1500 mm2;
Sono impiegati un calcestruzzo di classe 25/30, caratterizzato da:
-
fck = 25 MPa; σ cd =
0,85 ⋅ 25
= 14,17 MPa
1,5
ed un acciaio B450C, caratterizzato da
-
fyk = 450 MPa; f yd =
455
= 391,3 MPa ; Es = 210 000 MPa.
1,15
Si procede al calcolo del valore del momento resistente per la sezione in esame; si ha:
ω=
As f yd
bhσ cd
=
1500 ⋅ 391,3
= 0,2071 ⇒ y = h ⋅ ω = 500 ⋅ 0,2071 = 103,55 mm
400 ⋅ 500 ⋅ 14,17
Il braccio della coppia interna vale pertanto:
d * = d − 0,5 y = 460 − 0,5 ⋅ 103,55 = 408,23 mm
e quindi il momento resistente di progetto vale:
M Rd = T ⋅ d * = As f yd (d − 0,5 y ) = 1500 ⋅ 391,3 ⋅ 408,23 = 239,61 ⋅ 10 6 Nmm (= 240 kNm)
• Si supponga ora di considerare il legame elastico-incrudente per l’acciaio con k = 1.15 e k
= 1.35.
Caso a) k =
Il rapporto
ft
= 1,15, kf yd = 449,9 MPa
fy
x
è determinabile attraverso la relazione:
h
2
⎡
⎛ f
⎞⎤ x
⎛ f
⎞d
⎛x⎞
0,8⎜ ⎟ − ω ⎢1 − 0,08170⎜ t − 1⎟⎥ − ω ⋅ 0,05332⎜ t − 1⎟ = 0
⎜f
⎟⎥ h
⎜f
⎟h
⎝h⎠
⎢⎣
⎝ y
⎠⎦
⎝ y
⎠
2
x
x
⎛ x⎞
0,8⎜ ⎟ − 0,2045 − 0,0015 = 0 ⇒ = 0,263 ⇒ x = 0,263 ⋅ 500 = 131,5 mm
h
h
⎝h⎠
Il valore del momento resistente è pari a:
M Rd = 0,8σ cd bx(d − 0,4 x ) = 0,8 ⋅ 14,17 ⋅ 400 ⋅ 131,5 ⋅ (470 - 0,4 ⋅ 131,5) = 248,88 ⋅ 10 6 Nmm (= 249 kNm)
l’utilizzo del legame elastico incrudente con k=1,15 ha apportato, pertanto, un incremento di
momento resistente pari a:
∆=
M Rd ( k =1,15)
M Rd ( k =1)
Caso b) k =
=
249
= 1,037 (≅ 3,7%)
240
ft
= 1,35, kf yd = 528,3 MPa
fy
Si ha:
2
x
x
⎛ x⎞
0,8⎜ ⎟ − 0,2011 − 0,0036 = 0 ⇒ = 0,27 ⇒ x = 0,27 ⋅ 500 = 135 mm
h
h
⎝h⎠
M Rd = 0,8σ cd bx(d − 0,4 x ) = 0,8 ⋅ 14,17 ⋅ 400 ⋅ 135 ⋅ (470 - 0,4 ⋅ 135) = 254,65 ⋅ 10 6 Nmm (= 255 kNm)
l’utilizzo del legame elastico incrudente con k=1,35 ha apportato, pertanto, un incremento di
momento resistente pari a:
∆=
M Rd ( k =1,15)
M Rd ( k =1)
=
255
= 1,063 (≅ 6,3%)
240
• Si supponga ora di aggiungere un’armatura in compressione A’s = 500 mm2; e si consideri
per l’acciaio il legame elastico-plastico:
-
ω' =
A' s f yd
bhσ cd
base b = 400 mm;
altezza geometrica h = 500 mm;
altezza utile d = 460 mm;
copriferro c = 40 mm;
armatura in trazione As = 1500 mm2;
armatura in compressione A’s = 500 mm2.
=
500 ⋅ 391,3
= 0,069
400 ⋅ 500 ⋅ 14,17
Supponendo entrambe le armature snervate, si può calcolare y come:
y = h ⋅ (ω − ω ') = 500 ⋅ (0,207 − 0,0690) = 69,05 mm
L’ipotesi di armatura compressa snervata va controllata; l’armatura compressa è in campo elastico
solo se:
y ≤ 1,68c = 67,2 mm
e quindi, per il caso in esame, l’ipotesi di armatura compressa snervata è verificata.
La risultante di compressione è suddivisa nelle due componenti:
C1 = σ cd by = 14,17 ⋅ 400 ⋅ 69,05 = 391,38 ⋅ 10 5 N
C 2 = f yd A' s = 391,3 ⋅ 500 = 1,96 ⋅ 10 5 N
con risultante posizionata ad una distanza dal lembo superiore pari a:
dC =
C1 ⋅ 0,5 y + C 2 ⋅ c 391,38 ⋅ 0,5 ⋅ 69,5 + 1,96 ⋅ 40
= 34,77 mm
=
391,38 + 1,96
C1 + C 2
Quindi:
M Rd = T ⋅ d * = As f yd (d − d c ) = 1500 ⋅ 391,3 ⋅ (460 − 34,77) = 249,58 ⋅ 10 6 Nmm (= 250 kNm)
Esempio 3
Si consideri ancora la sezione dell’esempio 2 e si supponga di aggiungere uno sforzo normale Nsd
pari a 700 kN; si ha:
-
ν=
base b = 400 mm;
altezza geometrica h = 500 mm;
altezza utile d = 460 mm;
copriferro c = 40 mm;
armatura in trazione As = 1500 mm2;
armatura in compressione A’s = 500 mm2;
Sforzo normale Nsd = 700 kN
N sd
700 ⋅ 10 −3
=
= 0,247
bhσ cd 400 ⋅ 500 ⋅ 14,17
Supponendo entrambe le armature snervate, si può calcolare y come:
y = h ⋅ (ν + ω − ω ') = 500 ⋅ (0,247 + 0,2071 − 0,0690) = 192,55 mm
L’ipotesi di armatura compressa snervata va controllata; l’armatura compressa è in campo elastico
solo se:
y ≤ 1,68c = 67,2 mm
e quindi, per il caso in esame, l’ipotesi di armatura compressa snervata è verificata.
Inoltre, poiché risulta:
y < 0,522 d = 240,12 mm
anche l’ipotesi di armatura tesa snervata è verificata.
Quindi:
⎛h
⎞
⎛h− y⎞
M Rd = ybσ cd ⎜
⎟ + f yd ( As + A' s )⎜ − c ⎟ =
⎝2
⎠
⎝ 2 ⎠
⎛ 500 − 192,55 ⎞
6
= 192,55 ⋅ 400 ⋅ 14,17 ⋅ ⎜
⎟ + 391,3 ⋅ (1500 + 500 ) ⋅ (250 − 40 ) = 332 ⋅ 10 Nmm (= 332 kNm )
2
⎠
⎝
Esempio 4
Si consideri una sezione in cemento armato di caratteristiche geometriche:
- base b = 300 mm;
c= 4 cm
A's = 5φ16
h=60cm
- altezza utile d = 560 mm;
- copriferro c = 40 mm;
- armatura simmetrica (5φ16 = 10.05 cm2);
d=56cm
- altezza geometrica h = 600 mm;
c= 4 cm
As = 5φ16
b=30cm
Sono impiegati un calcestruzzo di classe 25/30, caratterizzato da:
-
fck = 25 MPa; σ cd =
0,85 ⋅ 25
= 14,17 MPa
1,5
ed un acciaio B450C, caratterizzato da
-
fyk = 450 MPa; f yd =
455
= 391,3 MPa ; Es = 210 000 MPa.
1,15
Si vogliono determinare le coordinate dei punti notevoli del dominio M-N (punti A-B- C-D-E).
Dominio M-N
300
D
"Metodo Rigoroso"
250
Punti notevoli
M (kNm)
200
150
E
C
100
50
A
-1000
ν=0
0
-500
0
ν=1
ν=0.5
500
1000
N (kN)
1500
2000
B
2500
3000
Punto A – (Trazione centrata)
A
A
N Rd
= −2 As f yd = −2 ⋅ 1005 ⋅ 391,3 = 786513 N = −786 kN; M Rd
=0
Punto B (Compressione centrata)
B
N Rd
= 2 As f yd + bhσ cd = 2 ⋅ 1005 ⋅ 391,3 + 300 ⋅ 600 ⋅ 14,17 =
B
= 786513 + 2550600 = 3337113 N = 3337 kN; M Rd
=0
Punto C (Flessione semplice) e Punto E
Il momento resistente può essere determinato in via approssimata mediante la seguente espressione:
C
E
M Rd
= M Rd
= As f yd (h − 2c ) = 1005 ⋅ 391,3 ⋅ (600 − 80) = 204493380 Nmm = 204,5 kN m
Si supponga adesso di voler effettuare il calcolo in via rigorosa.
Si osservi che in caso di armatura simmetrica è impossibile che l’armatura compressa sia snervata
in quanto in tal caso si arriverebbe all’assurdo che non ci sarebbe bisogno di calcestruzzo
compresso per l’equilibrio. Dunque in caso di armatura simmetrica sicuramente la profondità y deve
rispettare la disuguaglianza y ≤ 1,68c (ovvero armatura compressa in campo elastico).
cls
C1 = ybσ cd = 0.8 xbσ cd
acciao superiore
⎛ y − 0,8c ⎞
⎛
⎟⎟ = A' s E s ε cu ⎜1 −
C 2 = A' s σ s = A' s E s ε ' s = A' s E s ε cu ⎜⎜
y
⎝
⎝
⎠
(sfruttando la linearità del diagramma delle ε)
acciaio inferiore
T = As f yd
Eq. alla traslazione della sezione:
⎛
C1 + C 2 + T = 0 ⇔ 0.8 xbσ cd + A' s E s ε cu ⎜1 −
⎝
c⎞
⎟ − As f yd = 0
x⎠
moltiplicando tutto per x e sostituendo i valori numerici:
0.8bσ cd x 2 + (A' s E s ε cu − As f yd )x − A' s E s ε cu c = 0
3401x 2 + 345418 x − 2,95 ⋅ 10 7 = 0
La soluzione accettabile (> 0) è:
x=
− 345418 + (345418 2 + (4 ⋅ 3401 ⋅ 2,95 ⋅ 10 7 )
= 55,30 mm
2 ⋅ 3401
e quindi risulta ε ' s =
In definitiva:
x−c
55,30 − 40
ε cu =
⋅ 0,0035 = 0,00097 < εsy (= 0,00186).
x
55,30
c⎞
⎟
x⎠
T = As f yd = 1005 ⋅ 391,3 = 393256 N = 393 kN
C1 = 0,8 xbσ cd = 0,8 ⋅ 55,30 ⋅ 300 ⋅ 14,17 = 188064 N = 188 kN
⎛
C 2 = A' s E s ε cu ⎜1 −
⎝
40 ⎞
c⎞
⎛
⎟ = 204371N = 204 kN
⎟ = 1005 ⋅ 210000 ⋅ 0.0035 ⋅ ⎜1 −
x⎠
⎝ 55,30 ⎠
La risultante di compressione è posizionata a distanza dal lembo superiore pari a:
dC =
C1 ⋅ 0,4 x + C 2 ⋅ c 188 ⋅ 0,4 ⋅ 55,30 + 204 ⋅ 40
= 31,4 mm
=
188 + 204
C1 + C 2
e quindi il braccio della coppia interna risulta pari a:
d * = d − d C = 560 − 31,4 = 529 mm = 0,529 m
Dunque:
C
E
M Rd
= M Rd
= T ⋅ d * = 393 ⋅ 0.529 = 207,8 kN m
Dunque il calcolo per via approssimata conduce ad una sottostima del momento resistente pari a
∆ = 1−
204,5
= 1 − 0,98 = 0,02 (≅ 2%)
207,8
Punto E
E
N Rd
= bhσ cd = 300 ⋅ 600 ⋅ 14,17 = 2550600 N = 2550 kN
C
E
M Rd
= M Rd
= 207,8 kN m
Punto D
E
N Rd
= 1275 kN
2
E
N Rd
h
2550 0,6
C
= M Rd +
⋅ = 207,8 +
⋅
= 399,0 kN m
2 4
2
4
D
N Rd
=
D
M Rd
Dominio M-N
450
D
400
1275.0; 399.0
"Metodo Rigoroso"
Punti notevoli
350
M (kNm)
300
250
C
E
2550.0; 207.8
0.0; 207.8
200
150
100
50
A
-1000
ν=0
-786.0; 0.0
B
ν=1
ν=0.5
3337.0; 0.0
0
-500
0
500
1000
1500
2000
2500
3000
3500
4000
N (kN)
Un’ottima approssimazione del dominio (rispetto a quello ottenuto per via rigorosa si può avere:
-
unendo i punti A-C
-
utilizzando l’espressione M Rd = As f yd (h − 2c ) + N
h⎛
N ⎞
h
⎟⎟ = As f yd (h − 2c ) + N (1 − ν ) ⎜⎜1 −
2 ⎝ Nc ⎠
2
nel tratto C-D
unendo i punti D-E-B
Dominio M-N
450
D
400
"Metodo Rigoroso"
1275.0; 399.0
Punti notevoli
350
Costruzione semplificata dominio
300
M (kNm)
-
250
C
E
2550.0; 207.8
0.0; 207.8
200
150
100
50
A
-1000
-786.0; 0.0
-500
ν=0
B
ν=1
ν=0.5
3337.0; 0.0
0
0
500
1000
1500
N (kN)
2000
2500
3000
3500
4000