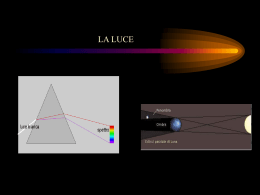
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
Riflessione, diffusione e rifrazione
Per meglio capire i princìpi della visione è necessario conoscere come si propaga la luce e come si
comporta quando incontra un “ostacolo”.
Una prima importante proprietà della luce consiste nel fatto che, se non viene ostacolata, essa si propaga in
linea retta.
Per rendersene conto basta osservare le ombre proiettate da oggetti illuminati da sorgenti di luce. Se le
sorgenti sono, o appaiono, piccole, le ombre sono più o meno nitide e la loro forma riproduce la sagoma
dell’oggetto illuminato. (Per avere un’ombra perfettamente nitida in qualunque situazione occorre avere una
sorgente di luce puntiforme. Le sorgenti di luce reali hanno una dimensione più o meno grande e questo
produce oltre alla zona d’ombra anche una zona di penombra la cui grandezza varia in funzione delle
dimensioni apparenti della sorgente e della distanza fra l’oggetto - l’ostacolo – e lo schermo sul quale
l’ombra viene proiettata.)
Un’altra dimostrazione di questa importante proprietà della luce: un oggetto si trova là dove lo vediamo
perché la luce che ci proviene da quell’oggetto è arrivata a noi seguendo un cammino rettilineo (se così non
fosse quando allunghiamo una mano per prenderlo non si troverebbe dove lo vediamo).
È chiaro che la luce può essere e viene deviata quando incontra un ostacolo; in queste pagine analizzeremo
alcuni modi in cui la luce cambia direzione. Per semplificare l’analisi selezioniamo un sottile pennello di luce,
un raggio di luce, che nelle rappresentazioni grafiche assimileremo a una retta.
Quando un raggio di luce incontra un ostacolo opaco o trasparente esso può essere riflesso, assorbito o
trasmesso (riflessione e assorbimento riguardano sia il corpo trasparente sia quello opaco, la trasmissione
solo quello trasparente).
La riflessione e la diffusione
Cominciamo con l’analizzare il comportamento della luce quando viene riflessa da un corpo di dimensioni
macroscopiche.
Se la superficie del corpo è liscia (ad
n o rm a le
esempio uno specchio o una superficie
metallica lucidata), allora la riflessione,
raggio incidente
raggio riflesso
nel caso ideale, è di tipo speculare e
segue la seguente legge: “il raggio
αi αr
riflesso giace sul medesimo piano
formato dal raggio incidente e dalla
normale
al
piano
di
Superficie riflettente
incidenza;
l’angolo fra il raggio incidente e la normale ha la medesima ampiezza di quello formato fra la
normale e il raggio riflesso cioè: angolo di incidenza uguale ad angolo di riflessione ( αi = α r )”.
Prof. M. Luraschi
Pagina 4
rev. aprile ’00
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
La riflessione speculare viene spesso indicata semplicemente con il nome di riflessione così che la legge
appena enunciata diventa la legge della riflessione.
Se la superficie del corpo è scabra (ad
n o rm a le
esempio un foglio bianco o la superficie
intonacata di un muro), allora la luce
raggio incidente
viene riflessa in modo diffuso e, nel caso
ideale, segue la legge di Lambert o
legge del coseno, vale a dire: “la luce
αi
viene riflessa in tutte le direzioni con
intensità che decresce secondo il
Superficie riflettente
coseno a partire dalla normale e
questo in modo indipendente dall’angolo di incidenza del raggio incidente ( I (α ) = I 0 ⋅ cos(α ) , dove
I 0 è l’intensità della luce diffusa in direzione perpendicolare alla superficie riflettente).”
La riflessione diffusa viene spesso indicata semplicemente con il termine di diffusione.
Se la superficie è quella di un corpo nero (ad esempio una superficie dipinta di nero fumo), allora il raggio di
luce non è né riflesso né diffuso ma viene assorbito e questo indipendentemente dall’angolo del raggio di
incidenza.
Naturalmente nessun corpo reale si comporta in assoluto come perfetto riflettore, perfetto diffusore o perfetto
assorbitore, ma i tre fenomeni, riflessione, diffusione e assorbimento sono presenti, in misura più o meno
importante, contemporaneamente. In particolar modo la porzione di luce riflessa specularmente o in modo
diffuso dipende dall’angolo di incidenza. Per la legge di conservazione dell’energia deve in ogni caso valere
che la somma della componente riflessa (specularmente o in modo diffuso) e della componente assorbita
deve corrispondere a quella incidente (indicata con
e con
1 l’intensità della luce incidente, con a quella assorbita
r quella riflessa vale: 1 = a + r ).
Si tenga inoltre presente che a tutto questo (in particolare per quel che riguarda la porzione di luce diffusa o
assorbita) si aggiunge la problematica colori.
Cosa succede quando il corpo colpito dalla luce ha dimensioni microscopiche?
Se le dimensioni dei corpuscoli sono ancora maggiori della lunghezza d’onda della luce (goccioline d’acqua,
cristallini di ghiaccio o particelle di fumo in sospensione nell’aria) allora la luce viene diffusa senza
distinzione di colore (le nuvole appaiono perciò bianche e il fumo bianco grigio).
Se a diffondere la luce è l’aria stessa (se la nostra atmosfera non diffondesse la luce, il cielo ci apparirebbe
anche di giorno nero come in una notte senza luna) allora la luce viene diffusa in proporzione alla quarta
potenza della propria frequenza (la definizione di lunghezza d’onda e frequenza verranno date in seguito;
per il momento basta sapere che una delle due grandezze è inversamente proporzionale all’altra); questo
spiega il colore azzurro del cielo e il colore rosso del sole al tramonto.
Prof. M. Luraschi
Pagina 5
rev. aprile ’00
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
La rifrazione
Esaminiamo ora cosa succede se il corpo sul quale la luce incide è trasparente.
Osserviamo ad esempio un raggio di luce che incide su una superficie d’acqua con angolo di incidenza
αi .
Dimenticando la diffusione (che è veramente trascurabile), si possono osservare chiaramente, oltre al raggio
incidente, un raggio riflesso e un raggio trasmesso (è evidentemente presente anche il fenomeno
dell’assorbimento, non osservabile in modo diretto, che trascuriamo in parte in questo paragrafo). L’intensità
dei raggi trasmesso e riflesso dipendono dall’angolo di incidenza
αi : si può facilmente osservare che
l’intensità del raggio riflesso, praticamente nulla con raggio incidente perpendicolare alla superficie, aumenta
con l’aumentare dell’angolo di incidenza; viceversa l’intensità del raggio trasmesso diminuisce con
αi . Analogamente a quanto visto per la riflessione a un corpo opaco, per la legge di
conservazione dell’energia, indicata con t la componente trasmessa, vale: 1 = a + r + t .
l’aumentare di
Interessiamoci ora della direzione del raggio trasmesso. Si può facilmente osservare che, come per la
riflessione, raggio incidente, raggio trasmesso e normale al piano di incidenza giacciono sul medesimo
piano; inoltre l’angolo che si forma fra il
raggio trasmesso e la normale alla superficie
di incidenza è sempre più piccolo di
αi .
raggio parzialmente
riflesso
raggio incidente
Quale relazione esiste fra i due angoli?
α
Questa relazione fu scoperta nel ‘600 dal
i
grande
pensatore
(Cartesio) e
francese
Decartes
indicando l’angolo fra il raggio trasmesso e la
normale con
aria
dal fisico olandese Snell;
acqua
α
α R vale:
R
sen (αi )
= n.
sen (α R )
raggio rifratto
(trasmesso)
Il fenomeno viene chiamato rifrazione, così
la relazione prende il nome di “legge della rifrazione” o “legge di Snell”, mentre
n che è una costante si
chiama indice di rifrazione e quello che finora avevamo chiamato raggio trasmesso diventa raggio rifratto e
α R angolo di rifrazione.
L’indice di rifrazione
n dipende dai due mezzi trasparenti (nel nostro esempio aia e acqua), detti mezzi di
propagazione (viene spesso indicato come indice di rifrazione relativo) nei quali avviene la rifrazione e può
essere determinato a partire dalla proprietà ottica di ciascun mezzo di propagazione chiamata indice di
rifrazione assoluto (vedremo, quando tratteremo il modello ondulatorio della luce, che l’indice di rifrazione
assoluto è associato con la velocità di propagazione della luce nel mezzo che è sempre più piccola della velocità della luce nel vuoto). Indicati i mezzi di propagazione con
sen (α1 ) n2
=
sen (α2 ) n1
Prof. M. Luraschi
oppure
1 e 2 , con α1 e α2 i rispettivi angoli vale:
n1 sen (α1 ) = n2 sen (α2 )
Pagina 6
rev. aprile ’00
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
Con la legge della rifrazione scritta in questo modo non ha più importanza conoscere in quale dei mezzi il
raggio incide oppure viene trasmesso.
Da notare che, fintanto che l’indice di rifrazione del mezzo in cui la luce incide è minore di quello in cui la
luce viene rifratta, la rifrazione è sempre possibile.
raggio parzialmente
riflesso
raggio incidente
raggio parzialmente
riflesso
raggio incidente
α
α
i
i
aria
aria
acqua
acqua
aria
raggio incidente
radente
acqua
α
α
α
raggio parzialmente
riflesso
R
R
R
raggio rifratto
raggio rifratto
raggio rifratto
Se invece l’indice di rifrazione del mezzo di propagazione del raggio incidente è maggiore di quello del
raggio rifratto, allora a partire da un angolo, detto angolo limite, non avremo più raggio rifratto ma solo raggio
riflesso detto raggio totalmente riflesso; tale fenomeno prende il nome di riflessione totale.
raggio rifratto
α
R
aria
aria
acqua
acqua
raggio rifratto
radente
acqua
α
α
aria
α
i
L
i
raggio incidente
raggio incidente
raggio parzialmente
riflesso
raggio totalmente
riflesso
raggio parzialmente
riflesso
raggio incidente
Per determinare il valore dell’angolo limite è sufficiente risolvere la relazione data dalla legge di Snell rispetto
all’angolo di incidenza (che in queste condizioni prende appunto il nome di angolo limite) ponendo l’angolo di
rifrazione pari ad un angolo retto, vale a dire:
n 
n1 sen (α L ) = n2 sen (90° ) da cui segue: α L = arcsen  2  .
 n1 
Nel caso del passaggio dall’acqua ( nacqua
Prof. M. Luraschi
= 1,33 ) all’aria ( naria ≅ nvuoto = 1 ) α L = arcsen( 1,133 ) = 48,7° .
Pagina 7
rev. aprile ’00
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
La dispersione dei colori
Quando un raggio di luce bianca subisce due volte la rifrazione entrando e uscendo da un prisma, si
produce quel fenomeno conosciuto come dispersione dei colori; si tratta di capire come questo avviene.
Cominciamo con il seguire il percorso di un raggio di
luce attraverso il prisma. Sia
n l’indice di rifrazione
γ
del prisma; con n = 1 per l’aria per la legge di Snell
si ha:
sen (αi ) = n sen (α R ) e n sen (βi ) = sen (β R ) .
Inoltre per ragioni geometriche
α
βi = γ − α R .
α
i
R
β
β
R
i
Combinando opportunamente le tre relazioni si
ottiene finalmente per
βR :
β R = arcsen (n sen (γ − arcsen (n1 sen αi ))) .
Se l’indice di rifrazione
n del prisma fosse costante
per tutti i colori non accadrebbe nulla di
particolare. In realtà l’indice di rifrazione
cambia (sia pure di poco) da colore a
colore (vedi tabella). Normalmente questa
piccola differenza non produce effetti visibili
salvo quando, in particolari situazioni, le
piccole differenze di indice di rifrazione
luce bianca
spettro
accentuano in maniera apprezzabile la
deviazione
dei
accade usando
colori,
un
come
appunto
prisma come nel
disegno.
Nella seguente tabella vengono riportati per due tipi di vetro e per i vari colori dello spettro i valori dell’indice
di rifrazione e tra parentesi l’angolo
Tipo di vetro
colore
flint
crown
β R per ciascun colore con αi = 60°
violetto
azzurro
verde
giallo
arancio
rosso
Indice di rifrazione 1,607
1,594
1,581
1,575
1,571
1,569
βR
(46,55)
(45,44)
(44,93)
(44,60)
(44,43)
Indice di rifrazione 1,532
1,528
1,519
1,517
1,514
1,513
βR
(41,08)
(40,37)
(40,21)
(39,98)
(39,90)
(47,67)
(41,41)
Si faccia attenzione che i colori indicati sono da intendere monocromatici; si sarebbe potuto tranquillamente
sostituire il nome di ciascun colore con la corrispondente lunghezza d’onda.
Prof. M. Luraschi
Pagina 8
rev. aprile ’00
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
Le lenti
In questo capitolo non si vuole analizzare come funziona una lente (rimandiamo questo a quanto già visto
nel corso si base), ma semplicemente riassumere le principali caratteristiche di una lente e come una lente
può essere utilizzata per produrre immagini reali o virtuali che siano.
Se facciamo passare un fascio di luce attraverso una lente, possiamo identificare le seguenti situazioni, a
seconda che si tratti di una lente convergente oppure divergente e che il fascio sia o meno parallelo all’asse
ottico,:
•
un fascio di luce (per fascio di
luce intendiamo un insieme di
lente
raggi di luce paralleli fra di loro)
incide su una lente convergente parallelamante all’asse ottico
(per asse ottico si intende quella
fascio di luce
distanza focale
asse ottico
retta che interseca perpendico-
fuoco
principale
larmente il centro geometrico
della lente). La luce convergerà
in un punto chiamato fuoco
principale della lente. La distanza, misurata sull’asse ottico,
fra il fuoco principale e il centro della lente viene chiamata distanza focale ed è, assieme al diametro
della lente, una delle caratteristiche principali della lente stessa.
La distanza focale può essere
più o meno grande a seconda
lente
della forma della lente e dal tipo
di materiale con cui è costruita.
Una
analisi
dettagliata
del
percorso di ciascun raggio di
fascio di luce
distanza focale
asse ottico
luce attraverso la lente può
fuoco
principale
essere fatta con la legge della
rifrazione. Senza entrare nei
dettagli si può comunque intuire
che, a parità di indice di rifrazione, più la lente è “panciuta”
più piccola è la distanza focale e viceversa.
Prof. M. Luraschi
Pagina 9
rev. aprile ’00
LUCE E VISIONE
•
I COLORI
APPUNTI DI FISICA
Un fascio di luce incide su una
lente convergente non paralle-
lente
lamente all’asse ottico. La luce
convergerà in un punto chiamato
fascio di luce
distanza focale
fuoco secondario. Con buona
approssimazione tutti i fuochi
asse ottico
secondari giacciono su un piano
fuoco
secondario
detto piano focale contenente il
fuoco principale. Dal punto di
vista geometrico il piano focale è
un piano perpendicolare all’asse
ottico contenente il fuoco principale.
•
Una lente può essere costruita
lente
per far divergere un fascio di
luce invece di farlo convergere;
in questo caso si parla di lente
divergente; il fuoco principale di
fascio di luce
distanza focale
asse ottico
una lente divergente è quel
punto sull’asse ottico dietro la
lente dal quale sembrano essere
originati
i
raggi
ottici.
fuoco
principale
Per
convenzione la distanza focale di
una
lente
divergente
viene
indicata con un valore negativo.
Individuate le principali caratteristiche di una lente occupiamoci ora di come una lente è in grado di produrre
immagini, siano esse reali, ad esempio quelle generate da un retroproiettore o da un proiettore per
diapositive o ancora quelle che l’obiettivo di un apparecchio fotografico produce sulla pellicola, siano esse
virtuali come ad esempio quelle ottenute guardando attraverso una lente di ingrandimento.
Prof. M. Luraschi
Pagina 10
rev. aprile ’00
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
L’immagine reale di una lente convergente
f e uno schermo sul quale
Se disponiamo nell’ordine, un oggetto, una lente convergente di distanza focale
osservare l’immagine generata
dalla lente si osserva che, una
lente
oggetto
volta fissata la distanza (indicata generalmente con
a ) fra
immagine
l’oggetto e la lente (vedremo
oggetto
che per ottenere una immagine
reale è necessario che valga
a > f ) esiste una sola distanza (indicata con b ) fra la lente
e lo schermo per avere una
lente
immagine
immagine “a fuoco”. Si osserva
inoltre che l’immagine è capo-
volta rispetto all’oggetto e che la sua dimensione e la sua distanza dalla lente dipendono dalla distanza fra
l’oggetto e la lente.
Il fatto che una lente è in grado di generare immagini nitide sullo schermo significa che i raggi di luce
generati da ogni singolo punto dell’oggetto devono convergere in un solo punto là dove si forma l’immagine
e questo deve valere per tutti i punti dell’oggetto. Per trovare dove questo avviene basta seguire il percorso
ottico dei singoli raggi attraverso la lente; dato che tutti i
lente
oggetto
raggi convergono nello stesso
1
punto basta seguire il percorso
immagine
3
di due che sceglieremo in base
2
alle proprietà delle lenti viste in
precedenza.
f
a
Dalla definizione di fuoco si può
f
b
dedurre che ogni raggio appartenente ad un fascio di luce parallelo all’asse ottico convergerà sul fuoco della lente (raggio no 1 nel
disegno); per simmetria ogni raggio di luce che passa per il fuoco di una lente uscirà parallelo all’asse
ottico (raggio 2). Esiste inoltre un terzo particolare raggio il cui percorso attraverso una lente è facilmente
descrivibile: si può infatti facilmente mostrare che un raggio di luce che passa per il centro della lente non
subisce alcuna deviazione (raggio 3).
Schematizzando in un nuovo disegno la situazione di una lente (doppia freccia), un oggetto di dimensione h
e la sua immagine di dimensione
H si può trovare, tramite la geometria dei triangoli simili, la relazione fra
a , b e f detta legge delle lenti sottili.
Prof. M. Luraschi
Pagina 11
rev. aprile ’00
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
a
b
f
f
A
h
F
F
H
A’
H
f
H b− f
H b
=
=
(triangoli con tratteggio chiaro),
(tratteggio medio),
(tratteggio scuro).
=
h a− f
h
f
h a
Da cui si può ricavare
1 1 1
= + la legge delle lenti sottili appunto.
f a b
Come già visto in modo sperimentale, quando l’oggetto si trova molto lontano dalla lente ( a
>> f ),
l’immagine, capovolta, si forma appena oltre il fuoco ed è molto piccola (questa situazione si presenta
tipicamente in un apparecchio fotografico, ammesso di poter assimilare ad una semplice lente convergente
la configurazione ottica dell’obbiettivo). Man mano che l’oggetto si avvicina alla lente si osserva che
l’immagine si allontana dalla lente e diventa via via sempre più grande (retroproiettore). Quando l’oggetto è
vicinissimo al fuoco, ma con
a > f , ci si trova nelle situazione tipica di un proiettore per diapositive (oggetto
molto piccolo e vicinissimo al fuoco della lente e immagine molto grande su uno schermo lontano).
L’immagine virtuale di una lente convergente
Che cosa succede ora se l’oggetto si trova
fra la lente e il fuoco? Come si può facilmente osservare i raggi di luce partenti da
lente
un punto dell’oggetto non convergono da
nessuna
parte.
Non
nessuna
immagine
si
reale
forma
1
3
perciò
dell’oggetto.
D’altro canto se si prolungano a ritroso gli
oggetto
immagine
virtuale
f
stessi raggi si osserva che i prolungamenti
f
a
convergono in un punto. Questo significa
b
che osservando l’oggetto attraverso la lente
lo si vede non nella posizione in cui si trova ma in quella da cui sembrano provenire i raggi di luce.
Prof. M. Luraschi
Pagina 12
rev. aprile ’00
LUCE E VISIONE
I COLORI
APPUNTI DI FISICA
Utilizzando una lente convergente in questo modo (lente di ingrandimento) si ottiene quella che viene detta
immagine virtuale di una lente convergente. Si osserva che l’immagine virtuale è sempre più grande
dell’oggetto e, contrariamente a quella reale che era capovolta, risulta diritta. Si può inoltre dimostrare che
anche in questa situazione vale la legge delle lenti purché si assuma come negativo il valore della
distanza b .
L’immagine (virtuale) di una lente divergente
Finora ci siamo occupati solo di lenti convergenti. Quale immagini produce una lente divergente?
Come per le lenti con-
lente
vergenti è possibile se-
1
guire il percorso degli
2
3
stessi raggi particolari.
Il raggio parallelo all’asse
ottico diverge come se
immagine
virtuale
oggetto
provenisse dal fuoco (1);
f
il raggio il cui prolungamento finisce sul fuoco
esce
parallelo
f
b
a
all’asse
ottico (2), mentre il raggio
che passa per il centro della lente non subisce deviazioni (3).
Come nel caso dell’immagine virtuale di una lente convergente non sono direttamente i raggi che
convergono in un punto bensì i loro prolungamenti. Si può facilmente osservare che per qualsiasi valore di
a l’immagine è sempre virtuale, diritta e rimpicciolita. Anche in questo caso vale la legge delle lenti perché
sia b che
f assumano valori negativi.
Prof. M. Luraschi
Pagina 13
rev. aprile ’00