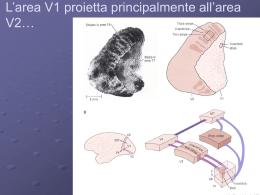
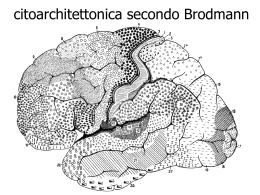
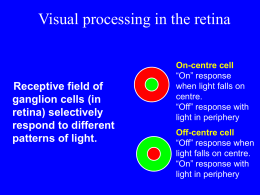
Analisi comportamentale del sistema
visivo
1
Modello lineare
Si puo mettere in evidenza il comportamento di un modulo a partire dalle relazioni note per
il campo recettivo . Ci interessa vedere il sistema come una sorta di "black box" (vedi g: 1)
Figura 1: Schema tipo "black-box" di un sistema
quindi determinare la relazione ingresso-uscita in modo da poter fare riferimento a questa per
simulare una elaborazione dell'informazione. In prima battuta siamo interessati a modelli lineari.
In proposito ricordiamo che un sistema e lineare quando:
vale il principio di sovrapposizione a cui corrisponde
s1 (t) ! e1 (t) =) s (t) + s (t) ! e (t) + e (t)
1
2
1
2
s2 (t) ! e2 (t)
a; b 2 <
as1 (t) + bs2(t) ! ae1 (t) + be2(t)
e vericata la continuita.
Se abbiamo una variazione parametrica dello stimolo in modo
continuo cio si riette parimenti sulla risposta.
sp (t)
! ep (t) =)
Z
sp (t)dp
!
Z
ep (t)dp
I principi di linearita sono applicabili sia allo spazio che al tempo. La rappresentazione del principio
Figura 2: La stimolazione di due punti distinti nel campo visivo provoca nell'ipotesi di linearita,
una risposta nel piano neurale pari alla somma delle risposte dovute a due stimoli presentati
singolarmente.
di sovrapposizione nello spazio e mostrato in (g: 2). Per lo studio comportamentale di un sistema
possiamo esaminare la risposta all'impulso h oppure la risposta in frequenza H . Sotto
l'ipotesi che un sistema sia lineare dato uno stimolo e una funzione di trasferimento possiamo
ricavare delle informazioni sulla risposta che tale sistema sara in grado di fornire. Se noi abbiamo
una funzione
Z
s(t) |{z}
! e(t) = h(t t0 )s(t0 )dt0
la risposta
1
Ragionando in termini di risposta in frequenza sottoponiamo il sistema a una serie di sinusoidi
note. In particolare pensiamo a delle sinusoidi come funzioni complesse nella forma
s(t) = ej!t = cos !t + j sin !t
(1)
e abbiamo come risposta
e(t) =
Z
ej!t` h(t t`)dt` =
e(t) =
Z
e
|
Z
ej!(t t`) h(t`)dt`
j!t` h(t`)dt`
{z
H (!)
ej!t
(2)
}
abbiamo cos individuato la funzione di trasferimento H (!) e la trasformata di Fourier della
risposta all'impulso come h(t). A livello sperimentale, nel caso della retina, si ricavano queste informazioni (nelle proprieta di risposta delle cellule visive alle diverse frequenze spaziali) utilizzando
come stimolo dei graticci di bande chiare e scure alternate in movimento (vedi g: ??.
Figura 3:
Pertanto in termini mono dimensionali otteniamo che dalla funzione
s(x; t) = ej(kx+wt)
(usata come stimolo) ricaviamo come risposta, sempre ragionando in termini di autofunzioni,
e(x; t) = H (k; w) ej(kx+wt)
dove con H (k; w) intendiamo
H (k; w) =
Z Z
e j(kx+wt) h(x; t)dxdt
e quindi la caratterizzazione della risposta in frequenza. Sfruttiamo invece una tecnica di indagine
impulsiva (dove gli impulsi sono delle singole barrette)sempre ipotizzando la presunta linearit
a del
sistema. Il passo seguente sara attuare un confronto diretto con i risultati del precedente studio
e vericare (attraverso la coincidenza dei risultati) la consistenza dell'ipotesi sulla linearita del
sistema in esame(vedi g: 4). Applicando l'ipotesi di linearita ad un sistema percettivo possiamo
descrivere la relazione tra un evento nel campo visivo ed una eccitazione nel piano neurale in
termini di funzione di trasferimento e risposta all'impulso. In un'analisi semplicemente temporale
notiamo che s(t) ! e(t) e per la linearita s(t t~) ! e(t t~) D'altra parte un discorso del genere
vale anche per lo spazio s(x) ! e(x) e per la linearita s(x x) ! e(x x)
In questo modo globalmente esprimiamo, una volta ssato nel piano neurale (x ; y )
e(x ; y ) =
Z
h (x0 ; y0; t t0 )s(x0 ; y0 ; t t0 )dx0 dy0 dt0
2
Figura 4: Schema a blocchi dell'analisi per la consistenza della linearita
e rileviamo che h dipende dalla posizione e cambia da punto a punto del piano neurale.
Diversamente se vale il principio di spazio-invarianza
e(x; y) =
2
Z
h (x x0 ; y0 y; t t0 )s(x0 ; y0; t t0 )dx0 dy0 dt0 :
Forma della risposta all'impulso
Se vogliamo dettagliare ulteriormente la risposta all'impulso notiamo che in alcuni casi possiamo pensare di separare la parte spaziale da quella temporale il che semplica ulteriormente la
trattazione. Possiamo cioe scrivere
h(x; y; t) = f (x; y) g(t)
La parte spaziale di tale funzione mostra la caratterizzazione del campo recettivo delle cellule
sensoriali. Con misure empiriche si e tentato di ricavare delle formule che approssimino i proli
di tali campi recettivi. L'elemento basilare di tali formulazioni e la forma geometrica Gaussiana
(a)
(b)
Figura 5: (a) Esempio di campi recettivi rappresentabili con una DOG e (b) prolo di una
Gaussiana.
(vedi g: 5).
G(x) =
A partire da questa deniamo:
p1 e
2
dierenze di gaussiane (DOG)
dierenze di gaussiane traslate (DOOG)
3
x2
2 :
derivate di gaussiane
Funzioni di Gabor
Il primo elemento consiste in DOG(x) = G(x; c )
G(x; s ) gracamente esposto in g: 6 In
Figura 6: La dierenza di due gaussiane permette di ottenere una DOG
presenza di uno stimolo costante l'integrale di tale dierenza si annulla. E` quello che verichiamo
in ambito retinico. Quando parliamo invece di DOOG arontiamo una descrizione che piu si
Figura 7: Dierenza di gaussiane traslate (DOOG) e campi recettivi associabili
avvicina alle cellule corticali (vedi g: 7). A livello analitico riportiamo
DOOG = A G(x; y; x ; y ) + B G(x xc ; y; x; y ) + C G(x + xc ; y; x ; y )
Un modello piu complesso che ricava le funzioni approssimanti dei campi recettivi derivando piu
volte una funzione Gaussiana G e il seguente.
Illustriamolo gracamente in g: 8.
Inne, per ultime (non per importanza), troviamo le funzioni di Gabor denite come (vedi
g: 9):
( 2x2x2 + 2y2y2 )
1
G(x; y) =
cos (2fo x + ')
e
2x y
Sono l'alternativa alle DOOG, alternativa migliore in quanto minimizzano l'incertezza nel
dominio dello spazio e della frequenza (massima risoluzione nello spazio e in frequenza).
L'incertezza e data dalla selettivita dei sistemi considerati, sia nello spazio, sia in frequenza.
x ; y ! Incertezza nello spazio. fx; fy ! Incertezza in frequenza.
x ; y ; fx; fy 161 ! si ha l'ugualianza solo con funzioni di Gabor.
3
Caratterizzazione in frequenza dei campi recettivi
La caratterizzazione dei campi recettivi in frequenza e la descrizione del comportamento del sistema
alle varie frequenze spaziali, per arrivare ad essa partiamo dalla conoscenza della forma del campo
recettivo nel dominio dello spazio per poi eettuarne la trasformata di Fourier.
Si ritiene opportuno continuare la trattazione servendosi di un esempio:
4
Figura 8: Derivate di gaussiane: varie combinazioni con relativi campi recettivi corrispondenti
Figura 9: Funzione di Gabor. ' = 0 ! Simmetria pari ' = 2
! Simmetria dispari.
Una funzione che possiede un campo recettivo nel dominio spaziale facilmente caratterizzabile
in frequenza e la funzione di Gabori (vedi g: 10:
G(x; y) =
( x2 + y2
1
e 2x2 2y2 cos(2fox + )
2x y
Applicando la trasformata di Fourier otteniamo (vedi g: 11:
FG^=G^(fx ; fy ) = 0:5e
22(x2 f2x +y2 f2y ) [ej Æ(fx
fo) + e jÆ(fx + fo )]
Gracamente eettuando la sezione lungo gli assi x e y del campo recettivo di Gabor nel
dominio della frequenza si ottiene la gura 12
Si possono individuare due parametri caratteristici:
la frequenza di picco;
la banda;
5
Figura 10: Campo recettivo di Gabor nel dominio dello spazio
Figura 11: Campo recettivo di Gabor nel dominio della frequenza
Circa la banda distinguiamo tra banda assoluta, la dierenza f = fh fl (tra la frequenza di
taglio superiore e quella inferiore calcolate come le frequenze per cui la frequenza di taglio raggiunge
valori pari a p12 del valore massimo), e la bada relativa. Come banda relativa intendiamo il rapporto
fra la banda assoluta e la frequenza portante f0 .
Bdf =
f
:
f0
Esiste pure la denizione di banda relativa in ottave denita come:
BOCT = log2 (fh ) log2 (fl )
Partendo da queste premesse traiamo degli strumenti per denire l'ottimalita dell'ampiezza della
banda. Dato un ltro molto selettivo nello spazio (vedi g: 13) e meno nelle frequenze possiamo
decidere di modicarlo. Elenchiamo le due alternative:
mantenere lo stesso inviluppo e modulare con una frequenza maggiore (f = cost: e f01 <
f02). Tutto cio aumenta il numero di lobi e privilegia la seletivita in frequenza (vedi g: 13).
ridurre l'inviluppo e contemporaneamente modulare con una frequenza piu piccola (vedi
g: 13.b). Una caratterizzazione in termini di bande assoluta e relative permette di osservare
nei due casi diversi comportamenti della banda relativa. (vedi g: 14)
Come criterio di ottimalita in questa scelta si cerca di avere BOCT = 1, infatti, ponendo BOCT = 1
si ottiene un buon compromesso tra selettivita nello spazio e in frequenza. Si tenga presente che
fh = f0 + 2f e fl = f0 2f per poter riscrivere
f + f
BOCT = log2 0 2f = 1
f0 2
Sviluppando si ottiene
2f0 + f
=2
2f0 + f
=)
2f0 + f = 4f0
6
2f
Figura 12: Tipico andamento in frequenza di un campo recettivo
(a)
(b)
(c)
Figura 13: Esempio di ltro e delle sue possibili trasformazioni : (b) stesso inviluppo e frequenza
modulante maggiore; (c) inviluppo ridotto e frequenza minore
2f0 = 3f
4
f
Il termine fo determina o meno una buona copertura in termini di frequenza (vedi g: 15:
In questo modo pensando all'espressione di una Gaussiana,
da modulare per ottenere il ltro di
q
log
2
1
g: 13, il valore della frequenza di taglio e pari a f = 2 e ricaviamo la frequenza ottimale
q
21
per modulare come f0 = 3 log
2 . Questi concetti trovano completa applicazione nelle funzioni
alla Gabor risultato di un prodotto di una gaussiana e funzione sinusoidale. L'utilizzo di tali
funzioni di Gabor come campo recettivo ci porta a un ulteriore incremento della complessita del
campo recettivo e delle prestazioni del modello percettivo relativo.
4
Modelli spazio varianti
Riprendiamo il discorso sulla funzione di trasferimento per quanto riguarda la caratterizzazione
rispetto ai piani retinico e corticale. Ribadiamo che in via del tutto generale la h dipende sia dalla
posizione sulla retina, sia dalla posizione sulla corteccia. Vogliamo ora esaminare nel dettaglio due
situazioni di trasformazioni da un piano all'altro:
Modello uno a uno: troviamo una corrispondenza biunivoca tra i punti dei due piani (vedi
7
(a)
(b)
Figura 14: Caratterizzazione in frequenza delle variazioni precedenti
Figura 15: copertura di un campo di frequenze: 4fof = COST (linea continua); 4fof = NON
COST (linea tratteggiata); in fo i due campi di copertura coincidono.
g: 16). Possiamo scrivere la trasformazione R : ! come
u = x
v = y
~x = (x; y) 2 e ~u = (u; v) 2
A questo scopo individuiamo anche un fattore di ingrandimento (Ma ) come determinante
dello jacobiano della trasformazione R:
Ma = jdetJR (~x)j
JR =
@Rx
@x
@Rx
@y
@Ry
@x
@Ry
@y
Modello molti a molti: si inttiscono i collegamenti ottenendo il modello di g: 16. In
questo caso posso pensare di ssare un punto sul piano e vedere come questo stesso va a
inuenzare l'attivita su , ottenendo la cosiddetta point spread function. Viceversa se
un punto e ssato sul piano corticale ottengo una denizione del campo recettivo:
h(~x; u ) = h (~x)
Considerazioni conclusive
Rileviamo che la selettivita dei campi recettivi puo essere legata a diversi parametri il piu
importante dei quali e certamente l'orientamento. A livello generale, denita una serie di parametri
p1 ; p2 ; :::; pn , senza escludere che questi stessi possano essere funzioni di ~u, una delle prime proprieta
da vericare e la dipendenza del campo recettivo dagli stessi (se un parametro varia con continuita
con la posizione o meno). Di conseguenza sara denita la funzione h(~x; p1 (~u); p2 (~u); :::; pn (~u))
8
(a)
(b)
Figura 16: I due modelli: a) modello uno a uno; b) modello molti a molti
Figura 17: Possibile evoluzione della g(t) e campi recettivi associabili
5
Comportamento temporale
Vogliamo ora esaminare quello che e il comportamento della funzione di trasferimento nel tempo, elemento nora trascurato avendo parlato diusamente della sola componente spaziale di
h(x; y; t) = f (x; y)g(t). A tal proposito possiamo rilevare come anche nel tempo non abbiamo un
comportamento statico ovvero assistiamo a una variazione della polarita che cambia le caratteristiche stesse di selettivita. Un esempio di prolo della funzione g(t) puo essere dato dalla g: 17
Figura 18: Esempio di campo recettivo che inverte la selettivita
6
Osservazione su blocchi non lineari in cascata
Si possono distinguere due tipi di non linearita:
9
6.1
Statiche
Dinamiche
Non linearita Statiche
Ricordiamo che una cellula nervosa non puo avere una frequenza di scarica negativa (una cellula
inibita, infatti semplicemente non rispondera). Per questo motivo le risposte negative ottenute
stimolando le sottoregioni negative dei campi recettivi lineari non hanno signicato siologico. Per
rendere piu coerente il modello di campi recettivi con la realta si possono introdurre dei blocchi
non lineari in cascata. Per comprendere il motivo della necessita di introdurre blocchi non lineari
in cascata consideriamo la classica funzione Gaussiana per l'approssimazione del campo recettivo
della retina:
Figura 19:
Supponiamo che la barretta eccitatrice (stimolo visivo) cada in una delle due regioni negative
della funzione, ne segue che la cellula non reagisce quindi non ottengo risposta.
Se introduciamo in cascata un blocco non lineare otteniamo risposta da parte della cellula in
quanto ad esempio il blocco introdotto potrebbe essere un raddrizzatore che eettua il ribaltamento
della zone dove la funzione e negativa.
Figura 20: Raddrizzatore a doppia semionda
Partiamo considerando la seguente situazione graca
Figura 21:
dove le risposte alla stimolazione (barretta), rispetto allo sfondo, sono di due tipi:
1) Stimoli piu chiari rispetto allo sfondo (risposta eccitatoria)
10
2) Stimoli piu scuri rispetto allo sfondo (risposta inibitoria)
Per avere una risposta corretta, bisogna fare in modo che non compaiono valori negativi. A
tal scopo si utilizza una serie di ltri (vedi g: 22):
Figura 22: sequenza di ltri lineari e non lineari
Retticazione a singola semionda: u = e+ = max(0; e). Questo tipo di retticazione viene
utilizzata per eliminare le parti negative della funzione considerata (vedi g: 23a.
Retticazione a doppia semionda: u = e+ e = max(0; e) + max(0; e). In tal caso si
ottiene il ribaltamento delle regioni negativi della funzione (vedi g: 23b.
Si impone anche una saturazione sull'uscita per evitare che il segnale cresca all'innito, e questo
lo si realizza tramite due tipi di funzioni lineari come ad esempio la funzione logica o sigmoidale.
Figura 23:
Funzione energia di un segnale
La funzione energia entra nel contesto in quanto e in grado di combinare le suddette simmetrie
(vedi g: 24):
Z
ec (x) = G(x0 )cos(x0 )s(x x0 )dx0
Z
G(x0 )sin(x0 )s(x x0 )dx0
hc (x0 ) = G(x0 )cos(x0 )
hs (x0 ) = G(x0 )sin(x0 )
es (x) =
Per rilevare la presenza di una barretta o di un graticcio con precisione non elevatissima, si
calcola, l'energia:
p
u = e2c + e2s
La precedente relazione prende il nome di "Funzione energia".
Ho dunque combinato due simmetrie per raccogliere piu elementi di una scena (vedi g: 25).
11
Figura 24: Funzioni di Gabor: (a) risposta pari; (b) risposta dispari.
Figura 25: Funzione energia
6.2
Non linearita dinamiche
Si rilascia l'ipotesi di tempo invarianza.
Si introducono sistemi adattivi (ltri adattivi).
Schema generale di un ltro adattivo (vedi:g 26)
Figura 26: s =segnale di ingresso, e =segnale di uscita,e =segnale di riferimento o condizionante
Esempio
12
Figura 27:
Se e e la risposta desiderata
Si parte da un problema di stima:
Vogliamo, " = e () e()
In generale, il segnale condizionante puo essere:
il contesto (rappresentato dalla risposta delle celle vicine)
{ caratteristiche dell'intorno
{ caratteristiche puntuali dello stimolo
{ la storia passata del sistema
informazioni a priori
{ un modello
{ una rappresentazione interna
Esempi
1) Normalizzatore
Figura 28:
13
2) Circuiti di eccitazione/inibizione
Figura 29: iterazione non lineare tra le risposte
14
Figura 30:
15