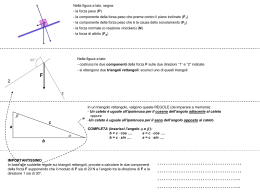
Teoremi sui triangoli rettangoli
Ai triangoli rettangoli possono essere applicati il TEOREMA DI PITAGORA, il PRIMO TEOREMA DI EUCLIDE e il
SECONDO TEOREMA DI EUCLIDE ma tali teoremi non permettono di determinare la misura degli angoli acuti del
triangolo. Noi ora vogliamo “risolvere un triangolo rettangolo”, cioè determinare la misura dei lati e degli angoli
acuti. Dobbiamo introdurre tre nuovi teoremi che permettono di risolvere il triangolo rettangolo, noti due dei
suoi elementi di cui almeno uno deve essere un lato.
Ricordando le definizioni di seno, coseno e tangente di un
angolo acuto e osservando l’angolo γ e la figura si ottiene :
senγ=
cosγ=
tangγ=
osservando l’angolo β si ottiene:
è la misura del lato opposto all’angolo
senβ=
cosβ=
tangβ=
che ha misura β,
c è la misura del lato opposto all’angolo …..
Dando denominatore comune si ottengono i tre teoremi dei triangoli rettangoli
b = senβ
c = senγ
In un triangolo rettangolo, un cateto è uguale all’ipotenusa per il seno
dell’angolo opposto al cateto
c = cosβ
b = cosγ
In un triangolo rettangolo, un cateto è uguale all’ipotenusa per il
coseno dell’angolo adiacente al cateto
b = c tangβ
c= b tangγ
In un triangolo rettangolo, un cateto è uguale all’altro cateto per la
tangente dell’angolo opposto al primo cateto.
Teoremi sui triangoli rettangoli
Ai triangoli rettangoli possono essere applicati il TEOREMA DI PITAGORA, il PRIMO TEOREMA DI EUCLIDE e il
SECONDO TEOREMA DI EUCLIDE ma tali teoremi non permettono di determinare la misura degli angoli acuti del
triangolo. Noi ora vogliamo “risolvere un triangolo rettangolo”, cioè determinare la misura dei lati e degli angoli
acuti. Dobbiamo introdurre tre nuovi teoremi che permettono di risolvere il triangolo rettangolo, noti due dei
suoi elementi di cui almeno uno deve essere un lato.
Ricordando le definizioni di seno, coseno e tangente di un
angolo acuto e osservando l’angolo γ e la figura si ottiene :
senγ=
cosγ=
tangγ=
è la misura del lato opposto all’angolo
che ha misura β,
osservando l’angolo β si ottiene:
senβ=
cosβ=
tangβ=
c è la misura del lato opposto all’angolo …..
Dando denominatore comune si ottengono i tre teoremi dei triangoli rettangoli
b = senβ
c = senγ
In un triangolo rettangolo, un cateto è uguale all’ipotenusa per il seno
dell’angolo opposto al cateto
c = cosβ
b = cosγ
In un triangolo rettangolo, un cateto è uguale all’ipotenusa per il
coseno dell’angolo adiacente al cateto
b = c tangβ
c= b tangγ
In un triangolo rettangolo, un cateto è uguale all’altro cateto per la
tangente dell’angolo opposto al primo cateto.