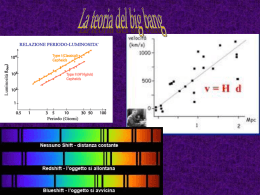
L’evoluzione delle galassie II
Amata Mercurio
INAF – OAC Napoli
“Due cose riempiono l’animo di
ammirazione e venerazione sempre
nuova e crescente, quanto più spesso
e più a lungo la riflessione si occupa
di esse: il cielo stellato sopra di noi e
la legge morale in noi.”
I. Kant
“…per quanto mi riguarda, io sono un ragazzo che
gioca sulla spiaggia e trova di tanto in tanto una pietra o
una conchiglia, più belli del solito, mentre il grande
oceano della verità resta sconosciuto dinnanzi a me…”
Isaac Newton
Res cogitans...
...Res extensa
L’uomo percepisce l’energia che pervade l’universo, ma
spesso non riusciamo a capirne l’origine.
• L’esistenza di una “causa prima”
• Il Big Bang
• Il problema cosmologico
• La materia dell’universo
“...se l’universo non avesse
avuto un inizio, ci sarebbe
stato un periodo di tempo
infinito prima di ogni
evento...”
I. Kant
“...se l’universo avesse
avuto un inizio, ci sarebbe
stato un periodo di tempo
infinito prima della sua
esistenza...”
I. Kant
Immanuel Kant
Edwin Powell Hubble
(1889-1953)
(1724-1804)
Nel 1926 Hubble fornisce
la prova definitiva che le
nebulose sono gli “universi
isola” di kantiana memoria.
Nel 1930 scopre la famosa legge di proporzionalità
tra la distanza e la velocità di recessione, detta
Legge di Hubble: V = Hd
…..ma prima del 1930
1916
La Relatività Generale interpreta la
gravità in modo nuovo:
non più come una forza misteriosa che
agisce a distanza fra corpi massicci, ma
come una proprietà dello spazio, il quale
risulterebbe deformato per la presenza
in esso della materia.
Lo spazio, pertanto è più quel contenitore vuoto e inerte entro il quale
agiscono gli oggetti materiali, ma diventerebbe esso stesso un prodotto
della materia.
Se prima di Einstein lo spazio poteva esistere anche senza la materia dopo
Einstein, se non ci fosse la materia, non esisterebbe nemmeno lo spazio.
Gli oggetti massicci, con il loro peso, deformano lo spazio,
provocano delle depressioni entro le quali tendono a scivolare
gli oggetti vicini.
L'attrazione tra gli oggetti non è prodotta da forze che
agiscono a distanza e istantaneamente, come pensava Newton,
ma è semplicemente la conseguenza di una particolare
configurazione che lo spazio assume a causa della presenza in
esso di oggetti massicci.
Se lo spazio tridimensionale tende spontaneamente ad incurvarsi, deve
disporre di una quarta dimensione entro cui poterlo fare.
Einstein pensò al tempo, ma non ad esso in quanto tale, bensì al tempo come
vera e propria dimensione spaziale. Questa quarta dimensione tuttavia
differisce dalle altre in quanto è caratterizzata da un’unica direzione: essa
va solo in avanti.
Dalla Relatività Generale, Einstein giunge al suo modello
di Universo
1917
Se la materia distorce localmente lo spazio, essa,
potrebbe conferire una curvatura generale all'Universo
intero, determinandone l'aspetto.
Modello di universo
statico

repulsione
attrazione
G
Dalla Relatività Generale, Einstein giunge al suo modello
di Universo
1917
Universo curvo quadridimensionale, illimitato ed infinito,
ma con dimensioni misurabili, anche se enormi.
Modello di universo
statico

repulsione
attrazione
G
Si andava facendo strada il
convincimento che l'Universo
non fosse fisso, immutabile ed
eterno, ma che si andasse
evolvendo nel tempo.
E infatti, proprio nel 1917
Willem de Sitter, dimostrò
che una soluzione delle
equazioni della Relatività
Generale suggeriva la
possibilità di un Universo in
espansione.
Il fisico e matematico russo
Aleksandr Friedmann chiarì
che le equazioni di Einstein
conducevano, in modo
spontaneo, ad una struttura
inequivocabilmente instabile di
Universo come potrebbe
essere ad esempio quella di
una matita in equilibrio sulla
punta.
La Teoria della Relatività Generale fornisce
dunque gli strumenti matematici per la
costruzione di quello che oggi viene definito
Modello Standard di Universo.
Il fisico russo Alexander Friedmann propone delle
equazioni, equivalenti alle equazioni del campo di
Einstein applicate al sistema-universo una volta che si
sia ipotizzato il principio cosmologico: L'universo è
omogeneo e isotropo, su di una scala opportunamente
grande.
Il Modello Standard, comunemente accettato,
è compatibile con le tre soluzioni di Friedmann.
In tale modello, l’Universo viene visto come una griglia la cui espansione
è descritta da una funzione a(t) detta fattore di scala, che dipende solo
dal tempo. Per esempio, se all’epoca attuale t0 la distanza d0 tra due
galassie è d0=l, all’epoca t (tt0) la distanza sarà d=a(t)l.
Il fattore di scala a(t), e quindi
l’evoluzione dell’universo, può avere
tre diversi andamenti, ognuno dei
quali dipende dal parametro di
densità misurato rispetto al valore
critico di densità dell’universo:
c*  10-29 gr/cm3.
 = oss. /c
*
c
= (3 H02)/(8G) con H0=75 km s-1 Mpc-1
Alle tre soluzioni di Friedmann corrispondono
tre diverse geometrie (modelli)
Gli universi “standard” di Friedmann
 c  densità critica


c
 1 aperto
 1 piatto
 1 chiuso
dimensione dell’universo
1922
aperti
chiuso
Geometrie
non euclidee
sferica
ora
tempo
piatta o
euclidea
iperbolica
Alexander Friedmann
(1888-1925)
UNIVERSO CHIUSO
Distanza tra due galassie
L’universo è finito ma non ha alcun
limite!
Big bang
Big crunch
tempo
MODELLO SFERICO (Tot< 1):
 L’espansione dell’Universo è lenta in modo che l’attrazione
gravitazionale tra galassie produca dapprima un rallentamento e
poi l’arresto.
 Il modello prevede una contrazione dell’Universo.
 All’inizio dell’espansione il raggio è zero (BIG BANG).
 Alla fine dell’espansione il raggio è zero (BIG CRUNCH).
 L’Universo ha curvatura positiva (K>0).
 Lo spazio è sferico, illimitato ma finito.
UNIVERSO PIATTO
Distanza tra due galassie
L’universo è infinito e l’espansione è tale
da evitare il suo collasso; è quindi piatto!
Big bang
tempo
MODELLO PIATTO (Tot= 1):
 L’espansione dell’Universo avviene con una velocità critica,
che è quella richiesta per impedirne la contrazione.
 Il modello prevede un’espansione dell’Universo senza fine, ma
sempre più lenta in quanto la velocità relativa tra le galassie
diminuisce senza mai annullarsi.
 All’inizio dell’espansione il raggio è zero (BIG BANG).
 L’Universo ha curvatura nulla (K=0).
 Lo spazio è piatto, illimitato ed infinito.
UNIVERSO APERTO
Distanza tra due galassie
L’universo è infinito, in continua
espansione e descrive una superficie “a
sella”!
Big bang
tempo
MODELLO IPERBOLICO (Tot> 1):
L’espansione dell’Universo avviene con una velocità sempre più
grande, e la forza di gravità non riuscirà mai ad arrestarla.
Il modello prevede un’espansione dell’Universo senza fine, con
le galassie che alla fine si espanderanno a velocità costante.
All’inizio dell’espansione il raggio è zero (BIG BANG).
L’Universo ha curvatura negativa (K<0).
Lo spazio ha la forma di una sella, è illimitato ed infinito.
Gli universi “standard” di Friedmann
 c  densità critica


c
 1 aperto
 1 piatto
 1 chiuso
Qualunque sia la soluzione è l’espansione iniziale
il primo motore
Il grande Scoppio
Big Bang
l’impulso è tale che il grave
sfugge per sempre
l’impulso è maggiore, ma non
ancora sufficiente
l’impulso è insufficiente
ed il grave ricade
massa M
Se la forza di
richiamo diminuisce,
uno stesso impulso
sortisce un effetto
maggiore
massa m < M
Edwin P.
Hubble
Nel 1929 Hubble, utilizzando il
più grande telescopio di quel
tempo, il riflettore di due metri e
mezzo di Monte Wilson, in
California, osservò lo
«spostamento verso il rosso» (red
shift) delle righe spettrali delle
galassie.
Questo fenomeno costituiva la
prova che quegli ammassi di stelle
si stanno allontanando da noi.
Hubble notò anche che quanto
maggiore era la distanza di una
galassia, tanto maggiore era la
sua velocità di allontanamento.
galassia
Questa relazione
lineare fra distanza
e velocità delle
galassie oggi si
chiama “legge di
Hubble” e può
essere espressa
nel modo
seguente: V = H·d,
dove V è la velocità
di allontanamento
della galassia, d la
sua distanza e H
una costante di
proporzionalità il
cui valore ha
subito nel tempo
numerose
correzioni e
aggiustamenti.
quella galassia.
Legge di Hubble
Distanza di luminosità
?
Quale dei modelli descrive il nostro universo?
Informazioni necessarie
Attuale velocità di espansione dell’universo
Attuale densità media dell’universo
Cosa sappiamo
• L’universo si espande del 5-10% per miliardo di anni
• La massa della materia luminosa + massa della
materia oscura = 1/10 della massa della materia
necessaria ad arrestare l’espansione dell’universo
• Non si può escludere che esista una qualche forma di
materia non ancora percepita da noi che sia in grado di
aumentare la densità media sino al valore critico.
• I dati disponibili indicano che l’universo è in perenne
espansione. Qualora dovesse nuovamente contrarsi, ciò
avverrà fra circa 10 miliardi di anni, tempo pari cioè al
periodo dell’attuale espansione.
• La relatività di Einstein può dimostrare che l’universo ha
avuto un inizio. Ma è insufficiente per svelarci in che modo
ciò sia avvenuto.
George Gamow
1948
Il fisico russo George Gamow
(allievo di Aleksandr
Friedmann), rifugiatosi per
motivi politici in Europa, e
successivamente trasferitosi
negli Stati Uniti, modernizzò e
perfezionò la teoria
dell'Universo in espansione di
Lemaître, che in seguito prese
il nome di «modello del Big
Bang»
George Gamow
1948
Se il big bang si verificò
effettivamente, dovrebbe
essere possibile rintacciare
ancora oggi il residuo delle
radiazioni elettromagnetiche di
quella gigantesca esplosione.
In particolare, 300 mila anni
dopo il big bang, quando
l'universo era ancora neonato, la
sua temperatura si sarebbe
abbassata fino a circa 4000
gradi.
George Gamow
1948
Ciò avrebbe reso possibile la
formazione degli atomi la palla di
fuco opaca dai primi momenti
sarebbe diventata via via più
trasparente, consentendo
all'universo di diventare visibile.
La luce di quell'epoca,che ancora
viaggia a causa dell'espansione
dell'universo, si sarebbe potuta
osservare sotto forma di
particolari onde
elettromagnetiche.
George Gamow
1948
Gamow suggerì l'esistenza di
una radiazione, residuo
raffreddato di quello che era
stato il globo di fuoco
dell'esplosione iniziale, come
effetto della continua
espansione e del conseguente
lento e graduale
raffreddamento dell'Universo.
George Gamow
1948
Secondo il modello del Big
Bang, insieme con l’espansione
dello spazio, avrebbe dovuto
dilatarsi anche l’onda
elettromagnetica, la quale, nei
primi istanti di vita
dell’Universo doveva essere
cortissima e carica di energia,
ma l’espansione la rese più
lunga fino a farla diventare
pari a quella che emergerebbe
da un corpo molto freddo (per
l’appunto alla temperatura di 3
gradi assoluti, cioè 270 °C
sotto zero).
Penzias & Wilson
1964
Nel maggio del 1964 quando due
ricercatori americani Arno Penzias e
Robert Wilson compiendo
esperimenti ai laboratori telefonici
BELL per la realizzazione di antenne
per comunicazioni satellitari
captarono interferenze sonore che
non si riusciva in alcun modo a
spiegare.
George Gamow
Penzias & Wilson
1964
In particolare captarono delle strane
micro onde della lunghezza d'onda di
3.2 cm che giungevano da ogni parte
dell'uiverso.
George Gamow
Penzias & Wilson
1964
Con l'aiuto del fisico Robert Dicke
dell'università di Princeton che
aveva ripreso la teoria di Gamow e
Bethe perfezionandola, si capì
finalmente che doveva trattarsi
proprio della fatidica radiazione di
fondo chiamata anche radiazione
fossile prevista dalla teoria del big
bang.
George Gamow
Penzias & Wilson
intensità
1964
Dati di COBE
rappresentati con un
Corpo Nero a
T = 2.736° K
lunghezza d’onda
George Gamow
COBE
Cosmic Background Explorer
Sulla base dell'osservazione
della radiazione cosmica di
fondo si può quindi
ragionevolmente affermare
che l'Universo era "nato"
molto caldo (Big Bang) e
poi si era progressivamente
raffreddato sino a
raggiungere "oggi" una
temperatura di 2.75 °
Kelvin e che, data la sua
estrema isotropia, le
ipotesi di isotropia ed
omogeneità erano
certamente valide almeno
fino al momento del
disaccoppiamento tra
radiazione e materia.
In un intervallo di tempo variabile
tra 1 sec < t Univ. < 3 minuti dall'inizio
del Big Bang. la densità e la
temperatura si riducono e la quantità
di barioni rimane "congelata" (se si
esclude il lento decadimento
spontaneo dei neutroni). Questo
avviene dopo circa 30 secondi dal Big
Bang e l'Universo ha dimensioni
paragonabili all'anno luce.
Dopo 100 secondi diventano efficaci
le reazioni nucleari. Protoni e
neutroni "fondono" tra loro dando
luogo al Deuterio (un isotopo
dell'Idrogeno composto da un
protone e un neutrone, e il cui
simbolo è 2H per indicare appunto la
presenza di due particelle), l'Elio
4He (composto da due protoni e due
neutroni), l'Elio 3He (un isotopo
dell'Elio con due protoni ed un solo
neutrone) e il 7Li (un isotopo del Litio
con quattro neutroni e tre protoni).
A questo punto la trasmutazione
degli elementi termina e la materia,
comprende quasi totalmente gli
elementi leggeri , ovvero i barioni
presentano un'abbondanza in massa
di circa il 77 % d'Idrogeno ed il 23%
di Elio.
Del Litio ci sono solo tracce mentre
tutti gli elementi pesanti (indicati
come "metalli" dagli astrofisici) sono
assenti; infatti essi verranno
prodotti molto tempo dopo tramite
le reazioni nucleari all'interno delle
stelle. Non c'è tempo per produrre i
"metalli" dal momento che
l'espansione riduce in fretta la
densità e la temperatura sotto la
soglia critica per l'innesco delle
reazioni nucleari.
Del Litio ci sono solo tracce mentre
tutti gli elementi pesanti (indicati
come "metalli" dagli astrofisici) sono
assenti; infatti essi verranno
prodotti molto tempo dopo tramite
le reazioni nucleari all'interno delle
stelle. Non c'è tempo per produrre i
"metalli" dal momento che
l'espansione riduce in fretta la
densità e la temperatura sotto la
soglia critica per l'innesco delle
reazioni nucleari.
Tutti gli elementi pesanti che
conosciamo vennero sintetizzati
successivamente all’interno delle
stelle, e rimessi in circolazione
dalle esplosioni stellari note come
supernovae.
Benché prodotto in scarsa quantità,
gli astronomi sono in grado di
misurarne l’abbondanza presente nel
gas interstellare in regioni
scarsamente "inquinate" dalle
successive esplosioni di supernovae.
Si può dunque risalire all’abbondanza
originale di deuterio e da questa, per
quanto detto prima, alla densità di
materia ordinaria. Essa risulta
essere circa quattro volte superiore
a quella luminosa.
Valori di :
 Dalla nucleosintesi
 Tot~ 10-1
E' noto già da alcuni decenni che la massa delle galassie deve essere
molto maggiore – fino a 10 volte – di quella luminosa (cioè stelle e
gas). Benché non la si possa vedere direttamente, possiamo dedurre la
presenza di questa massa in eccesso dai suoi effetti gravitazionali: le
stelle nelle galassie hanno velocità così alte che la gravità dovuta alla
loro mutua attrazione non sarebbe sufficiente a trattenerle e le
galassie si smembrerebbero rapidamente. Analogamente, le galassie in
un ammasso si allontanerebbero velocemente le une dalle altre se a
trattenerle non fosse una gravità superiore a quella data dalla loro
reciproca attrazione. Pertanto, negli ammassi deve essere presente più
materia scura di quella associata alle singole galassie.
Inoltre, questa materia "misteriosa" potrebbe trovarsi anche negli spazi
tra galassie ed ammassi di galassie.
Calcolo della massa M di una galassia all’interno di
una data distanza radiale R:
vR
MR

R
NGC 1035
G m MR = m VR2
R2
m
R
NGC 2998
 MR = R VR2
G
forza centrifuga
forza gravitazionale
Raggio
VR
MR
VR
MR
(kpc) (km/s) (1010 MO) (km/s) (1010 MO)
G = 6.670 x 10-8
0.5
39
0.018
87
0.088
1.0
65
0.098
102
0.24
2.0
91
0.39
126
0.74
1 pc = 206265 U.A.
3.0
107
0.80
142
1.40
1 U.A. = 1.496x1013 cm
5.0
123
1.80
182
3.90
8.0
135
3.40
204
7.70
1 pc=3.086x1018 cm
20.0
214
21
30.0
214
32
(dyn cm2 g-2)
1 MO = 1.989x1033 g
Curva di rotazione
Esprime la velocità di rotazione delle stelle all’interno di
una galassia in funzione della loro distanza dal centro
Si costruisce utilizzando le righe d’emissione (se presenti
 componente gassosa) e/o d’assorbimento (componente
stellare) dello spettro della galassia
I()  profilo osservato di una riga

0

I(o)  profilo in laboratorio della
stessa riga
La riga osservata sarà spostata per effetto Doppler di 
rispetto alla riga di laboratorio
Parametri cinematici: si derivano dallo studio spettroscopico
Componenti di uno spettro:
Continuo stellare
Righe d’assorbimento
(componente stellare)
Righe d’emissione
(componente gassosa)
 La fenditura dello spettrografo può essere posta lungo
uno qualsiasi degli assi della galassia .
 Generalmente, viene posta lungo l’asse maggiore che
coincide con la linea dei nodi e lungo la quale si ha la
massima velocità di rotazione della galassia .
 vc è la velocità del baricentro della galassia. Ad ogni
distanza x dal centro della riga corrisponde un volumetto
di stelle dV posto a distanza R dal centro della galassia
che si muove con velocità vi e dispersione di velocità i
(corrispondente all’allargamento della riga in quel punto).
 In questo modo è possibile costruire un grafico ponendo in
ascissa la distanza dal centro della galassia (posto come
origine) ed in ordinata la corrispondente velocità di
rotazione media: vi = c(i - c)/c.
Un grafico analogo può essere costruito con le dispersioni
di velocità i.
Tipico profilo delle
dispersioni di velocità
Curva di rotazione
tipica
si ha: gas  star  vgas  vc
Componente gassosa  struttura “fredda”
Componente stellare  struttura “calda”
UGC 2936
[NII] H
[NII]
dispersione
-10”
0
10”
6640 Ǻ blueshift
6650 Ǻ redshift
300 km/s
200
100
0 + Vel. Sist.
-100
-200
-300
Radius
Dispersione
Lungo la fenditura
6640 Ǻ blueshift
6650 Ǻ redshift
NGC 5746
M83
NGC 5236
dispersione
NGC 4111
Nucleo contro-rotante
NGC 3593
Lo spettro può essere
realizzato anche attraverso
una successione continua di
immagini monocromatiche
della fenditura.
Sia S ( ) lo spettro di una
sorgente uniforme
attraverso una fenditura
infinitamente sottile.
Attraverso una fenditura lo
spettro é:
NGC 891
F ( ;  )
s ( )  S ( )  F ( ;  ) 

 S (t ) F (  t;  )dt

Curva di
rotazione della
Via Lattea
all’osservatore
linea dei nodi
k
s e n sono due versori

n s
 i
V  (r ) n  r
r

V




Vlos  V  s  (r ) n  r  s  (r ) s  n  r 
 
 (r ) k  r sin i  (r ) cos  sin i
z
A

B
i
A
B
V ( R,  )  Vsys  V ( R) sin i cos 
300
Orbita kepleriana
200
100
Sol
e
Velocità orbitale (km/s)
Curva di rotazione della Galassia
20.000
40.000
Distanza dal centro galattico (anni luce)
60.000
Interpretazione della curva di rotazione:
vR
(c)
(a)
(b)
R0
R
Le curve di rotazione delle galassie presentano un andamento
come sopra: si possono distinguere le due componenti a e c :
 tratto (a) : la velocità di rotazione cresce linearmente con
la distanza fino ad R0;
 tratto (c) : per R > R0, al crescere della distanza, la velocità
resta costante o diminuisce lievemente.
Il tratto (b), per R > R0, corrisponde al moto kepleriano e non
è osservato
Significato fisico:
M

R
P
Nel tratto (a) la galassia si comporta come un corpo
rigido: in ogni punto P posto a distanza 0<R<R0 dal centro
della galassia si ha equilibrio tra forza di gravità e
forza centrifuga  la materia esterna a tale punto non
esercita alcuna forza su di esso.
Nel punto P posto a distanza 0<R<R0 dal centro della
galassia sarà:
v2/R = G(M/R2)
con
M = (4/3)  q R3 
v2 = (4/3)  G q R3  R2
posto: K = [(4/3)  G q R3 ]1/2 = cost.
si ha: v = K R
In questo modo è spiegato il tratto (a) della curva
di rotazione.
Dalla relazione precedente segue:
 = (3 K2)/(4  G q R3) = cost.
la
densità
all’interno del volume di raggio R = R0 è costante.
Un punto P’ posto a distanza R’ > R0 dal centro della galassia si
muoverà per effetto della forza esercitata su di esso dalla
massa contenuta all’interno dell’ellissoide avente a = R = R0.
Per tutti questi punti si dovrebbe osservare un moto
kepleriano, un moto la cui velocità decresce al crescere
della distanza dal centro del moto secondo la seguente legge:
v2/R = G(M/R2)
ma: (GM)1/2 = cost
v = K’ R-1/2 con K’ = (GM)1/2 = cost.
M = cost.
In questo tratto non è la densità che resta costante ma è
la massa che resta costante
M = cost  (4/3)  G q R3 = K’’  = [(3 K’’)/4 G q] R-3
  R-3
 nel tratto (b) la densità di massa è una funzione che
decresce come il cubo della distanza.
Cosa ci dicono le osservazioni:
 La velocità non decresce in modo kepleriano (v  R-2)
 La velocità resta pressoché costante
v2/R = G(M/R2)  v2 = (4/3)  G q R2 
da cui segue:
v =cost    R-2
 nel tratto (b) la densità di massa è una funzione che
decresce come il quadrato della distanza
 In questo tratto la densità decresce meno rapidamente di
quanto previsto dal moto kepleriano
Presenza di materia oscura che fa crescere il rapporto
M(R)/L(R) verso l’esterno.
(R)
 tratto (a) :  = cost.
(a)
(c)
(b)
R0
 tratto (b) :   R-3
 tratto (c) :   R-2
R
 Il tratto kepleriano (b) della curva di rotazione,
corrispondente a v  R-2 e   R-3, non viene osservato.
 Dopo il tratto (a) di corpo rigido (v  R e  = cost.) le
velocità di rotazione restano costanti o, in pochi casi,
diminuiscono più lentamente (  R-2) rispetto a quanto
previsto dal moto kepleriano (  R-3)  esiste materia
oscura nelle regioni esterne delle galassie
Qual è il valore della
Problema della
densità dell’universo?
massa mancante
Evoluzione dell’universo
Galassie lontane
Problema dell’osservazione di template e galassia
Stella
Galassia
Problema dell’osservazione di template e galassia
Lo spettro osservato della galassia è la somma degli
spettri delle singole stelle che contribuiscono lungo la
linea di vista
2
Moto delle stelle
 Vr  vr 2 
n(vr )  exp  

2
2 r 

Distribuzione gaussiana
Spettro di una stella
Si(x)
S1(x - ũi)
x = ln λ
+
S2(x - ũi)
+
otteniamo
S3(x - ũi)
+
.....
G (x)
Spettro osservato di una stella
con velocità vi=c · zi
Si(x - ũi)
ũi = ln (1+zi)
SN(x - ũi)
Spettro di una galassia
G (x) = Σi=1N Si(x - ũi)
N→∞
G (x) = ∫B(ũ) S(x - ũ) d ũ
B(x) ⊗ S(x)
B(x) (broadening function) rappresenta la distribuzione di velocità delle
stelle lungo la linea di vista:
B(x) ∝ exp ( - x2 / 2σ2)
σ = dispersione di velocità
Determinazione della massa di una galassia
….sostituendo nel teorema del viriale, si ottiene:
- GM/<R> = <v>2
Le quantità fisiche presenti in questa espressione, possono essere legate
alle quantità osservate:
σ2 ∝ <v>2
r ∝ <R>
Ottenendo, così, una stima della massa:
M = - r σ2 /G
Valori di :
 Dalla dinamica
 Dalla nucleosintesi
 Tot~ 10-1
 Tot~ 10-1
La nostra Galassia fa parte del Gruppo Locale di cui è il membro più grande
insieme alla galassia di Andromeda e ad una trentina di galassie
nane. Ebbene, tutte queste galassie – un autentico torrente di stelle – si
muovono a 600 km/s verso un punto del cielo ribattezzato il Grande
Attrattore; tuttavia, puntando i telescopi in questa direzione non si nota
nulla di particolare.
Potrebbe dunque esserci un enorme aggregato di materia scura che ci
attrae in questa direzione.
In generale, il conteggio di galassie in grandi volumi di universo
osservabile indicano che la materia scura è circa 30 volte più
abbondante di quella luminosa.
Si tratta di capire quale sia la natura di questa materia
scura. Potrebbe essere composta da una miriade di piccoli oggetti delle
dimensioni di pianeti, oppure buchi neri, che risulterebbero del tutto
invisibili ai nostri telescopi.
In realtà gli astronomi sospettano che la maggior parte della materia
scura non sia formata dall’ordinaria materia barionica (protoni e
neutroni) ma da qualche forma di materia non ordinaria.
Materia scura calda
Durante il Big Bang sono state create enormi quantità di neutrini. Benché la
loro massa sia molto piccola, il loro numero è tale che immensi "nuvoloni"
iniziali di neutrini avrebbero potuto sviluppare una gravità tale da collassare su
sé stessi, formando le prime strutture. Essendo molto leggeri, i neutrini si
muovono a velocità vicine a quella della luce. In analogia ai gas ordinari, in
cui la velocità di agitazione termica determina la temperatura, questo tipo di
materia scura viene detta "calda".
Materia scura fredda
Le attuali teorie sulle particelle elementari prevedono che, nelle condizioni
presenti nei primi istanti del Big Bang, si formino particelle genericamente
denominate WIMPS (Weakly Interacting Massive Particles). Contrariamente ai
neutrini, la reale esistenza di queste particelle non è stata ancora verificata nei
laboratori di fisica. A causa della loro massa elevata, infatti, la produzione di
tali particelle richiede energie enormi non ancora disponibili negli attuali
acceleratori di particelle. Essendo più pesanti dei neutrini, queste particelle si
muovono più lentamente, e la materia scura in questo caso viene detta
"fredda".
Dark matter
Not dark matter
Nel quadro della materia scura calda, strutture di piccola massa non
sono inizialmente in grado di collassare a causa dello "sciamare" dei
neutrini in ogni direzione. In questo caso si sarebbero formate
dapprima le grandi strutture, quali gli ammassi di galassie. Solo
successivamente queste si sarebbero "frammentate" in oggetti più
piccoli come le galassie.
Questo schema gerarchico viene detto top-down (dall’alto in
basso). La materia ordinaria (protoni e neutroni) che compone le
galassie che osserviamo è poco abbondante ed esercita una gravità
trascurabile. Essa si aggrega non a causa della propria gravità, ma a
causa della formazione delle strutture di materia scura verso cui è
attratta.
Dark matter
Not dark matter
Nello scenario della materia scura fredda, invece, i WIMPS, più
lenti e pesanti, formano dapprima strutture relativamente piccole
all’interno delle quali viene attratta la materia ordinaria che dà
luogo a piccoli ammassi stellari o galassie nane. Solo
successivamente, in un processo detto merging, queste strutture
più piccole si attraggono formando galassie ed ammassi di galassie.
Merging di galassie vengono effettivamente osservati, ma non
sappiamo se si tratta di episodi isolati o di un processo generale che
sta alla base della formazione delle galassie più grandi.
Questo schema di formazione delle strutture viene detto bottomup (dal basso in alto).
Dark matter
Not dark matter
Le simulazioni numeriche tramite grandi calcolatori mostrano che la
materia scura calda, a causa di questa sua caratteristica, è "restia"
a collassare in strutture relativamente piccole. Dopo 15-20 miliardi
di anni (l’età stimata dell’universo) le simulazioni mostrano una
presenza eccessiva di grandi strutture ed una penuria di strutture
minori rispetto alle osservazioni dell’universo su larga scala. Al
contrario, la materia scura fredda, nonostante alcune difficoltà di
cui non ci occupiamo in queste pagine, sembra riprodurre bene la
distribuzione osservata di materia luminosa.
http://www.galletta.it/gg/conferenze/filmati.htm
Dark matter
Not dark matter
WIMP esotici, come il fotino, sono stati predetti da una teoria detta
supersimmetria (SUSY). Questa teoria prevede, per ogni particell,a
l’esistenza del suo corrispettivo –ino. Queste particelle, però, hanno vita
molto breve e “esistono” solo nell’Universo primordiale. Infatti vivono
solo in un Universo governato da altissime energie: 100 GeV. L’Universo,
nel raffreddarsi rompe la supersimmetria.
Nel nostro Universo, potrebbero ancora sopravvivere, come, per
esempio partners del fotone, ma con masse tra 10 e100 volte quella del
protone, senza carica, e con un’interazione debolissima con la materia,
quindi davvero difficili da rivelare.
Dark matter
Not dark matter
Ci sono forti evidenze in favore di SUSY dagli esperimenti
condotti al CERN, che misurano la forza delle interazioni nucleari.
Ma, ovviamente, non si arriva alle enormi energie dell’Universo Già
energie da10 a15 GeV sono molto più alte di quelle che si possono
raggiungere negli esperimenti. Solo SUSY arriva a descrivere le
altissime energie, e potrebbe fornire una struttura teorica al
problema della inevitabile grande unificazione delle forze.
Dark matter
Not dark matter
Pertanto gli astronomi sono portati a preferire l’ipotesi di una
materia scura fredda, nonostante quest’ultima, al contrario dei
neutrini, sia solo ipotizzata dalle attuali teorie sulle particelle
elementari e non sia stata ancora osservata. I futuri sviluppi nello
studio dell’infinitamente piccolo saranno illuminanti per la
comprensione dell’infinitamente grande.
Dark matter
Not dark matter
La presenza di materia oscura ha importanti conseguenze
sull’evoluzione dell’Universo e della sua struttura. La quantità totale
di massa e di energia, infatti, determinano il valore di , e ci dicono
se l’Universo è chiuso, piatto o aperto.
Gli universi “standard” di Friedmann
 c  densità critica


c
 1 aperto
 1 piatto
 1 chiuso
Nota: La dinamica dell’Universo non è determinata interamente dalla
geometria, in quanto esso non contiene solo materia. Infatti il valore
di  viene in maggior parte dalla l’energia, in particolare dalla
cosiddetta dark energy.
Modello di universo

repulsione
attrazione
G
Nota: La dinamica dell’Universo non è determinata interamente dalla
geometria, in quanto esso non contiene solo materia. Infatti il valore
di  viene in maggior parte dalla l’energia, in particolare dalla
cosiddetta dark energy. Quindi, per capire davvero cosa accade
all’universo, dobbiamo calcolare il suo “fattore di espansione per i
casi specifici della densità di materia e dell’energia.
Valori di :
 Dalla dinamica
 Dalla nucleosintesi
 Dalla teoria dell’inflazione
 Tot~ 10-1
 Tot~ 10-1
 Tot= 1
Scenari evolutivi
Esistono due scenari che cercano di spiegare i processi di formazione ed
evoluzione delle galassie:
Scenari evolutivi
Collasso monolitico.
In questo scenario (Larson, 1974,
MNRAS, 166, 585), la formazione
delle galassie avviene in un’epoca
remota, quando la formazione
stellare ha inizio simultaneamente
per tutte le galassie.
L’evoluzione delle galassie è
passiva, cioè è conseguenza
dell’evoluzione delle stelle che
popolano le galassie.
Scenari evolutivi
“Merging” gerarchico
In questo scenario, sistemi più
piccoli che si sono formate in
epoche remote, si fondono per
formare sistemi sempre più grandi
col trascorrere del tempo.
L’evoluzione
delle
galassie
è
attiva, cioè è conseguenza degli
incontri e/o delle fusioni tra
galassie.
Gli episodi di fusione tra galassie
sono osservati sia nell’universo
vicino (in misura minore) che
nell’universo lontano (in misura
maggiore).
Scenario del “merging” gerarchico
 Inizi degli anni ’70: punto di partenza della teoria del “merging”
gerarchico per spiegare i processi di formazione
delle galassie ellittiche (Toomre& Toomre, 1972,
ApJ, 178, 623). Tale teoria si basa sia su dati
osservativi che teorici.
Secondo questa teoria, le galassie che si osservano (sia ellittiche
che spirali) sono il risultato di un processo di assemblaggio a
partire da sistemi sempre più piccoli.
Scenario del “merging” gerarchico
A seconda delle masse coinvolte nei processi di fusione, si possono
avere due diversi tipi di “merging”:
1.“Merging” minore: le masse dei sistemi coinvolti sono molto
differenti tra di loro (10:1, 100:1, 1000:1, …): il risultato finale sarà
la galassia maggiore con i segni del “merging”.
2.“Merging” maggiore: le masse dei sistemi coinvolti sono confrontabili
tra di loro (da 1:1 a 5:1): il risultato finale sarà una nuova galassia
completamente diversa dalle due hanno dato origine al “merging”.
Lo scenario del “merging” gerarchico si basa sul paradigma della
“Cold Dark Matter” (CDM).
Formazione delle galassie ellittiche
Scenario del collasso monolitico:
Le galassie ellittiche si sono formate dal collasso di una gigantesca
nube di gas;
 la nube collassa in modo omogeneo, formando le stelle e consumando
quasi del tutto il gas presente, dando origine agli oggetti che noi oggi
osserviamo (Peebles, 2002; Chiosi & Carraro, 2002);
 questo spiegherebbe facilmente l’omogeneità delle
osservate nelle galassie ellittiche (Jimenéz et al., 1998);
proprietà
Formazione delle galassie ellittiche
Scenario del collasso monolitico:
le galassie ellittiche sono sistemi vecchi, che si sono formati a
z > 2 e che evolvono passivamente (Peebles, 2002; Chiosi &
Carraro, 2002);
 le galassie ellittiche che si sono formate come conseguenza di
un merging sono poche rispetto a quelle “normali”;
 nello scenario del collasso monolitico, il “merging” non riveste
un ruolo chiave nel processo di formazione delle galassie
ellittiche.
Formazione delle galassie ellittiche
Scenario del “merging” gerarchico:
 le galassie ellittiche sono il risultato di un “merging” maggiore
tra due dischi, dopo che il sistema finale si sia completamente
rilassato (virializzazione del sistema);
 le galassie ellittiche possono essere viste come l’ultimo stadio
dell’evoluzione delle galassie (Baugh et al., 1996, MNRAS, 283,
1361);
 le galassie ellittiche sono sistemi relativamente giovani, che si
sono formati a z < 2 (Baugh et al., 1996, MNRAS, 283, 1361;
van Dokkum et al., 1999, ApJ, 520, L95), mentre le stelle di
cui sono composte possono essere più vecchie.
Formazione delle galassie ellittiche
Esistono evidenze osservative a supporto di entrambi gli
scenari:
ad alzo z si osservano le così dette Ultra Luminous Infrared
Galaxies (ULIG’s) che possono essere sia il risultato di un
collasso monolitico, che il risultato di “merging” tra galassie
(Genzel et al., 2001, ApJ, 563, 527);
 è stato osservato che il “merging” tra galassie è più frequente
nel passato che nel presente (Burkey et al., 1994, ApJ, 429,
L13);
 c’è un’evoluzione nel numero di sistemi sferoidali osservati nel
centro degli ammassi;
 mentre nel passato si osserva un numero maggiore di sistemi a
disco, ad epoche recenti si osserva un numero maggiore di
galassie “early-type”, soprattutto nelle regioni centrali degli
ammassi  l’ambiente svolge un ruolo determinante
nell’evoluzione delle galassie.
“Ram Pressure Stripping”
Si definisce “Ram Pressure Stripping” la perdita del gas
presente in una galassia (ISM – Interstellar medium) per
effetto della sua interazione col gas caldo presente all’interno di
un ammasso (ICM – intercluster medium) .
Per una galassia che si muove all’interno di un ammasso, l’effetto
che subisce è analogo a quello di un vento che strappa il gas in
essa contenuto solo se la sua forza è tale da vincere la forza
gravitazionale della galassia che tiene il gas legato a sé.
Il risultato finale della “Ram Pressure Stripping” è una galassia
che contiene solo una piccola quantità di gas freddo  questo
processo può alterare in modo drammatico la storia evolutiva di
una galassia.
Nelle simulazioni che seguono, fatte nel sistema di riferimento
solidale con la galassia in movimento, viene rappresentata la
variazione della densità del gas in funzione del tempo per una
galassia a disco che si muove all’interno di un ammasso ricco,
come quello di Coma, ad una velocità di 2000 km/s (Mach 1.9). Il
tempo-scala tipico di queste simulazioni è di 108 anni.
“Galaxy strangulation”
“Galaxy strangulation” rappresenta un altro processo
efficiente attraverso il quale le galassie che si trovano
all’interno di un ammasso possono perdere il loro gas.
Quando una galassia entra in contatto per la prima
volta con l’ambiente di un ammasso, il potenziale
gravitazionale di quest’ultimo crea effetti mareali che
portano alla perdita del gas presente all’interno della
galassia.
Man mano che questo gas si disperde all’interno
dell’ammasso con l’ICM, viene a mancare sempre più il
carburante necessario per la formazione stellare
all’interno della galassia, che quindi diminuisce fino ad
arrestarsi.
In poche parole, la formazione stellare cessa perché la
galassia, privata del proprio gas, viene strangolata.
“Galaxy harassment”
All’interno degli ammassi le intererazioni tra galassie sono abbastanza
frequenti.
Si definisce “galaxy harassment” un passaggio ravvicinato tra due
galassie a velocità sostenuta.
Il “galaxy harassment” può disturbare o addirittura modificare
radicalmente le morfologie delle galassie coinvolte, dando anche luogo
a nuovi episodi di formazione stellare.
Alcuni effetti prodotti dal “galaxy harassment” da un punto di vista
osservativo sono:
 presenza di galassie asimmetriche;
 presenza di galassie disturbate;
 presenza “warps” nelle strutture delle galassie;
 presenza di barre;
 presenza di code mareali.
“Galaxy harassment”
Lo studio di galassie che hanno subito “harassment” è importante
per almeno due motivi:
1) gli effetti prodotti dal “galaxy harassment” possono essere
usati per determinare la distribuzione della materia, sia
oscura che luminosa, per le galassie coinvolte;
2) Il “galaxy harassment” ed altri tipi di interazione possono
giocare un ruolo importante nella storia evolutiva delle
galassie.
Perché studiare le galassie negli ammassi
Lo studio delle galassie d’ammasso costituisce un efficace strumento per
vincolare i meccanismi che stanno alla base dei processi di formazione ed
evoluzione delle galassie attraverso:
1) analisi della LF  fornisce informazioni sui processi stellari che avvengono
nelle galassie;
2) analisi della relazione “colore – magnitudine”, della relazione “Mg2 - 0”,
e dei “gradienti di colore”  forniscono informazioni sulle proprietà delle
popolazioni stellari nelle galassie in funzione della distanza dal centro, quali:
a) età; b) metallicità; c) contenuto di polveri.
3) analisi delle relazioni tra parametri strutturali  fornisce informazioni
sulle proprietà delle galassie a diversi redshift, sia attraverso lo studio di
correlazioni che attraverso l’analisi di come queste quantità dipendano da .
Funzione di luminosità delle galassie
Introduzione
Definizioni:
Funzione di luminosità delle galassie
 la funzione di luminosità (LF) (M)dM rappresenta il numero di galassie per unità di
volume e di magnitudine;
 la quantità (M)dM è proporzionale al numero di galassie che hanno magnitudine
assoluta compresa nell’intervallo (M, M+dM);
 la quantità (M)dMdV = N, rappresenta il numero N di galassie nel volume V;
 la LF viene normalizzata ponendo:  (M)dM = N/V = , dove  è il numero di galassie
per unità di volume.
Proprietà:
 la LF è un utile strumento per confrontare l’universo reale con quello ottenuto mediante
le simulazioni cosmologiche;
 l’evoluzione della LF con il redshift permette di ottenere informazioni sull’evoluzione
delle galassie;
 gli effetti dell’ambiente sulla LF permettono di discriminare i possibili meccanismi che
possono dar luogo alla trasformazione delle galassie.
Dipendenza:
 dalla banda fotometrica.
 dai parametri strutturali delle galassie;
 dalla distanza.
La LF può essere rappresentata mediante data la funzione di
Schechter (Schechter, 1976, ApJ, 203, 297):
(M) = 0.4ln(10) *10 0.4 (M* - M) ( + 1) exp[-10 0.4 (M* - M) ]
Nella funzione precedente, *, M*,  sono tre parametri liberi
scelti in modo da interpolare nel modo migliore possibile i dati
osservativi.
La formula precedente assume un aspetto più semplice se, invece
delle magnitudini, si considerano le luminosità.
Se si assume che sia (L)dL il numero di galassie con luminosità
compresa nell’intervallo (L, L+dL), la LF assume la seguente forma:
Dove L* è la luminosità di una galassia avente magnitudine assoluta
M*.
Nella funzione di Schechter,  è la pendenza della LF a basse
luminosità; * è il fattore di normalizzazione spaziale, cioè il
numero N di galassie per Mpc3;
L* (M*) è la luminosità
(magnitudine assoluta) corrispondente al cosiddetto “ginocchio”
della LF.
Dipendenza dei parametri della LF:
  può dipendere dalla posizione spaziale (campo, ammasso) e dal
redshift;
  ed L* (M*) possono dipendere dal tipo morfologico e dal
redshift.
, , L* (M*) contribuiscono separatamente alla LF totale.
Ci danno informazioni sulla formazione delle galassie.
Andamento della LF:
1) il numero di galassie diminuisce “monotonicamente” con il crescere
della luminosità;
2) alle magnitudini assolute più deboli, (M) decresce in modo
esponenziale fino ad una certa magnitudine caratteristica M*, in
prossimità della quale si ha una netta variazione di tendenza.
Nelle 3 figure a lato è
mostrato come varia la
LF al variare dei tre
parametri liberi.
Esempio di LF in diverse bande fotometriche:
LF per galassie dell’universo vicino (z < 0.1) ottenute utilizzando dati della
SDSS nelle 5 diverse bande fotometriche della survey.
In basso a ciscuna LF è riportata la distribuzione delle magnitudini
assolute delle galassie utilizzate per determinare la corrispondente LF.
(Blanton et al., 2001, AJ, 121, 2358)
Dipendenza della LF dal redshift (dati SDSS):
Dai dati della SDSS
emerge che non c’è alcuna
dipendenza dal redshift
(evoluzione
temporale)
fino a z = 0.15.
z = 0.15
z = 0.05
Con i dati della SDSS è stato possibile produrre la LF nell’universo vicino (z < 0.1).
Per studiare una possibile evoluzione della LF col redshift è necessario utilizzare
osservazioni pù profonde che ci consentano di arrivare a redshift elevati, per es. a z ~
5.
Bisognerà tenere in considerazione il fatto che a redshift così elevati, la radiazione
sarà anche “spostata verso il rosso” rispetto a z = 0.
Nella tabella che segue viene riportata la banda corrispondente ad un dato redshift,
diverso rispetto a quello di riposo:
U
B
V
R
U
B
V
R
I
J
H
K
L
M
(3650 Å)
(4450 Å)
(5510 Å)
(6580 Å)
(8060 Å)
(12200 Å)
(16300 Å)
(21900 Å)
(34500 Å)
(47500 Å)
0
0.22
0.51
0.80
1.21
2.34
3.47
5.00
8.45
12.01
0
0.24
0.48
0.81
1.74
2.66
3.92
6.75
9.67
0
0.19
0.46
1.21
1.96
2.97
5.26
7.62
0
0.22
0.85
1.48
2.33
4.24
6.22
Per esempio, la radiazione emessa nell’UV (3650 Å,) a z = 5 viene vista in banda K (21900 Å)
LF a diversi intervalli di z:
I dati delle curve a lato sono tutti
compatibili con  = 1.15.
I valori degli altri due parametri  e M*
evidenziano una chiara evoluzione della LF
col redshift.
In particolare, M* diminuisce con z: 
nella banda UV ( = 2800 Å) le galassie, una
volta, erano molto più brillanti.
Poiché la luminosità UV a  = 2800 Å è
legata al tasso di formazione stellare della
galassia dalla relazione:
SFR (M☼ / yr) = 1.27x10-28 L(UV) erg s-1 Hz-1
Le curve sono spostate di 1 dex in
ordinata per ogni intervallo di z.
è possibile studiare come è variato il tasso
di formazione stellare alle varie epoche.
(per esempio, Madau et al., 1998, ApJ, 498, 106)
Dipendenza della LF
dal tipo morfologico
LF risultante per galassie di
campo di diverso tipo morfologico
LF risultante per galassie di
ammasso di diverso tipo morfologico
E’ possibile derivare la LF per
ciascun tipo morfologico.
Dipendenza della LF dal tipo morfologico:
La LF ottenuta con i dati della “Las Campanas Redshift Survey” è diversa per le
galassie i cui spettri non hanno righe di emissione (E – S0) e per le galassie i cui
spettri hanno righe di emissione (Sa – Irr) (Lin et al. ApJ, 464, 60)  esiste una
dipendenza morfologica della LF;
LF per diversi tipi morfologici (Jerjen & Tammann, 1997, AA, 321, 713):
(Sa – Sc)  gaussiana con <MB> = -16.8 + 5 log h e B = 1.4;
S0  gaussiana con <MB> = -17.5 + 5 log h e B = 1.1;
E  gaussiana modificata per tener conto di un eccesso di galassie brillanti, con:
<MB> = -16.9 + 5 log h e B = 2.2 se MB < <MB> oppure B = 1.3 se MB > <MB>;
Irr  grossolanamente con una Schechter con parametri:
 = -0.3 e MB* = -15 + 5 log h;
dE
 LF simile a quella delle Irr, con parametri:
 = -1.3 e MB* = -16 + 5 log h;
Non è ancora chiaro se esista una LF universale per ciascun tipo
morfologico;
se dovesse esistere una LF universale per ciascun tipo
morfologico, essa dovrebbe contenere informazioni sull’origine
della classe di oggetti cui si riferisce;
se dovesse esistere una LF universale per ciascuna classe di
galassie, essa potrebbe essere utilizzata come indicatore di
distanza;
l’esistenza o meno di una LF universale per ciascun tipo
morfologico resta un problema dell’astronomia extragalattica.
LF negli ammassi di galassie
Le galassie d’ammasso si trovano in un ambiente completamente diverso
dalle galassie di campo per quanto riguarda i processi di formazione ed
evoluzione.
Diventa interessante confrontare la LF delle galassie di campo con la LF
delle galassie appartenenti, per esempio, ad ammassi ricchi.
Vantaggi nella determinazione della LF per galassie in ammasso:
le galassie dell’ammasso sono distribuite in su una regione limitata di cielo,
per cui è più facile ottenere la fotometria;
le galassie si trovano tutte alla stessa distanza, per cui basta conoscere la
distanza dell’ammasso per ricavare le magnitudini assolute.
Problemi:
 Gli ammassi ricchi sono rari e distanti  diventa difficile ottenere la
fotometria per le galassie più deboli.
Risultati del confronto tra LF di campo e ammasso (banda B):
La forma è la stessa (funzione di Schechter) ma cambiano i parametri:
 * è più grande, a causa della maggiore densità di galassie presenti in un
ammasso;
 M* = -19.5  0.1 + 5 log h è simile al valore delle galassie di campo;
  = -1.27  0.04 è minore rispetto al valore trovato per le galassie di campo 
sebbene la magnitudine M* di cut-off sia simile, la pendenza della parte più
debole della LF è più ripida per le galassie d’ammasso;
 la LF non sembra variare molto da ammasso ad ammasso e sembra essere
riproducibile, in modo ragionevole, da una semplice funzione di Schechter anche
se la presenza di sotto-struture, diverse da ammasso ad ammasso, può rendere
complicata la rappresentazione con una semplice funzione di Schechter (Lugger,
1986, ApJ, 303, 535);
 in molti ammassi, la LF si discosta da una semplice Schechter a causa della
presenza di un avvallamento a MB ~ 16 + 5 log h, e ad un eccesso di galassie nella
parte più brillante;
 la presenza di questo eccesso di galassie brillanti negli ammassi era stata
evidenziata anche da Schechter nel suo lavoro originale (Schechter, 1976, ApJ,
203, 297);
 il problema è capire se la presenza di quest’eccesso di galassie brillanti sia una
caratteristica di tutti gli ammassi.
Evidenza osservativa:
Effetti dell’ambiente
le galassie “early-type” si trovano più facilmente e con maggiore
frequenza negli ammassi piuttosto che come oggetti isolati, al
contrario delle galassie “late-type”;
esiste una correlazione tra la frazione f(E) di galassie ellittiche
presenti in un ammasso e la forma dell’ammasso: gli ammassi con
grande f(E) hanno una struttura regolare e simmetrica, con una
ellittica gigante al loro centro, mentre ammassi con piccola f(E)
presentano un aspetto irregolare (Oemler, 1974, ApJ, 194, 1);
all’interno degli ammassi regolari, esiste una segregazione dei
tipi morfologici, nota come relazione morfologia-distanza, nel
senso che la quantità di spirali, all’interno di un ammasso
regolare, diminuisce dall’esterno verso l’interno, fino ad
annullarsi nel core. Un andamento opposto si ha per le ellittiche;
la segregazione morfologica comporta, come conseguenza, una
differenza cinematica tra i diversi tipi morfologici;
Evidenza osservativa:
Effetti dell’ambiente
il fatto che le spirali si trovino preferibilmente all’esterno
dell’ammasso significa che seguono orbite più energetiche e
quindi, ad una certa distanza dal centro, le loro dispersioni di
velocità sono più elevate rispetto a quelle delle ellittiche  le
spirali sono in fase di caduta verso il core virializzato
dell’ammasso.
Dressler (1980, ApJ, 236, 351): primo studio sistematico sulla
segregazione morfologica su un campione di ~ 6000 galassie in 55
ammassi.Trova che f(Sp) cresce con R e, più in generale, una
relazione tra tipo morfologico ed ambiente.
Relazione Morfologia - Densità
La relazione morfologia-densità è una relazione di
tipo osservativo tra il tipo morfologico delle galassie
e l’ambiente, definito come il numero di galassie vicine
per Mpc3.
Dalla relazione morfologia-densità si ricava che le
gallasie early-type (ellittiche e S0) si trovano,
preferenzialmente, in ambienti molto densi, mentre
le galassie late-type (spirali) preferiscono gli
ambienti meno densi.
 Le galassie a spirale sono rare nelle regioni più
dense degli ammassi, e si trovano più
abbondantemente nelle regioni meno dense o
come oggetti isolati.
 Le galassie early-type abbondano nelle regioni più
dense (centro degli ammassi) e si trovano molto
di rado nella periferia degli ammassi o come
oggetti isolati.
Si crede che la relazione morfologia-densità sia una
consequenza del fatto che l’evoluzione delle galassie
possa essere in qualche modo influenzata
dall’ambiente in cui si trovano. In particolare, molte
evidenze osservative ci indicano che la formazione
stellare all’interno delle galassie viene inibita dagli
ambienti molto densi (ammassi).
Relazione morfologia-densità per galassie spirali, S0,
ed ellittiche. Man mano che si procede da ambienti
meno densi ad ambienti più densi la popolazione di
galassie dominante cambia da late (spirali) ad early
(S0 ed ellittiche).
La causa di ciò non è ancora ben nota.
Alcuni tra i processi più efficienti che si pensa
possano essere la causa dell’inibizione della
formazione stellare sono:
a) ram pressure stripping;
b) galaxy harassment;
c) galaxy strangulation.
Proprietà generali delle galassie in funzione dell’ambiente
(Sorrentino, Delogu & Rifatto, 2006
 La luminosità è un parametro cruciale quando si vogliono studiare le proprietà
delle galassie in funzione dell’ambiente;
 in media, un ambiente “sotto-denso” (vuoto) è popolato da galassie più blu
rispetto a quelle che si trovano in ambienti molto densi (ammassi);
 in media, galassie deboli (Mr > -21) sono più blu se si trovano in ambienti “poco
densi” rispetto a quando si trovano in ambienti “densi”. La transizione di colore
dal blu al rosso, man mano che si passa da ambienti “poco densi” ad ambienti
“molto densi” è più pronunciata quando si considerano galassie più deboli (Mr > 21);
 sebbene la transizione da ambienti “poco densi” ad ambienti “molto densi” sia più
pronunciata per le galassie deboli, non sembra che ci sia discontinuità nelle
proprietà delle galassie;
 le variazioni nella distribuzione del colore (u – r) sono legati all’ambiente, alla
luminosità ed alla morfologia. Infatti, in media, le galassie “più deboli” (Mr > -21)
sono più blu, late-type e si trovano in prevalenza in ambienti “poco densi”
rispetto alle galassie più brillanti (Mr < -21) che sono, in media, più rosse, earlytype ed in ambienti prevalentemente “più densi”;
 non esiste dunque alcuna discontinuità nelle proprietà delle galassie quando si
passa da ambienti “poco densi” ad ambienti “molto densi”, al contrario di quanto
precedentemente asserito da Peebles (2001, ApJ, 557, 495).
Evoluzione del tipo morfologico
 La relazione morfologia - densità potrebbe essere spiegata come
dovuta agli effetti dell’interazione tra galassie.
 Ma se questa è la spiegazione, perché non si nota alcuna evoluzione di
questa relazione da z = 0.5 (circa il 60% dell’età dell’universo) ad oggi?
Il problema consiste nel fatto che non è possibile osservare lo stesso
ammasso man mano che evolve.
Il tempo evolutivo delle galassie all’interno di un ammasso dipende dalla
sua densità  se si osserva un ammasso ricco ad alto redshift e lo si
confronta con un ammasso vicino di analoga ricchezza, in realtà si
confrontano ammassi con età evolutiva simile  non sorprende il fatto
che non si osservi alcuna evoluzione nella relazione morfologia – densità.
I tipi morfologici potrebbero dunque evolvere a causa delle interazioni
tra galassie, ma la scelta dei campioni di ammassi a redshift diversi non
è semplice e quindi rende difficile il confronto.
Evoluzione del tipo morfologico (z > 1):
Per z > 1 lo studio dell’evoluzione morfologica di una galassia presenta
problemi aggiuntivi legati, per esempio, al fatto che bisogna applicare la
cosiddetta correzione K morfologica, ossia al fatto che il tipo morfologico
di galassie uguali osservate nella stessa banda ma a redshift diversi
apparirà diverso.
L’esperienza “locale” ci dice che il tipo morfologico di una galassie dipende
molto dalla banda d’osservazione:
M81:
M81:
FUV – NUV
bande g,r, i
(1516 – 2267 Å)
(5000 – 7200 Å)
GALEX
Palomar, 1.5m
(2006, astro-ph/6440G)
(1996, AJ, 111, 174)
Il modo corretto per fare le osservazioni è quello di scegliere una banda (per esempio,
B) ed usarla ad ogni redshift.
Nel visibile è possibile studiare l’evoluzione della morfologia delle galassie fino a z = 1.
Per andare a redshift più alti bisogna ricorrere alle osservazioni nell’IR.
Dipendenza della LF dal tipo morfologico (dati SDSS):
(Nakamura et al., 2003, AJ, 125, 1682)
MDLF nella banda r*
per tre classi morfologiche
rappresentate da simboli diversi: cerchi vuoti ( E - S0),
triangoli pieni (S0a – Sb), e quadrati vuoti (Sbc – Sd). Le
corrispondenti LF sono indicate con una linea continua, con
una linea a tratti corti e con una linea a punti,
rispettivamente. La LF corrispondente alle galassie irregolari
è indicata con una linea a tratti e punti, mentre la LF totale è
indicata con i simboli a croce ed una linea a tratti lunghi. Gli
istrogrammi sottostanti rappresentano la distribuzione in
magnitudine delle galassie in ciascun campione.
MDLF per galassie early-type e late-type classificate
utilizzando l’indice di concentrazione C. I cerchi aperti
rappresentano i dati per le galassie early-type (C < 0.35),
mentre i triangoli pieni rappresentano i dati relativi alle
galassie late-type (C > 0.35), con le corrispondenti LF
(linea piena e tratteggiata, rispettivamente). I dati relativi
al campione totale sono rappresentati con le croci e la
corrispondente LF con una linea a tratti lunghi. Gli
istogrammi sottostanti rappresentano le distribuzioni in
magnitudini dei campioni di galassie usate.
Dipendenza della LF dalla brillanza superficiale e dal
colore (dati SDSS):
LF per diversi intervalli di
brillanza superficiale
LF per diversi intervalli del
colore (g* - r*)
LF nel super ammasso di Shapley (Mercurio et al., 2006, MNRAS, 368, 109):
 Area di 2 gradi quadrati a z ~ 0.05;
 campione di galassie completo a B = 22.5 (N = 16588) e R = 22.0 (N = 28008);
LF totale
 la LF non può essere descritta da una semplice funzione di Schechter (S) ma dalla
combinazione di una gaussiana (G) per la parte brillante e da una Schechter per la
parte più debole;
 questo risultato è determinato dalla presenza di un avvallamento presente a B ~ 17.5
(R ~ 17.0) e ad una chiara risalita a B e R ~ 18.0
LF relativa all’intera area considerata in banda B (sinistra) e R (destra). Le linee
tratteggiata e continua si riferiscono all’interpolazione di una S e di una G+S,
rispettivamente
Effetti dell’ambiente
 regioni a bassa densità: la LF deve essere rappresentata mediante una
combinazione G+S in entrambe le bande;
 regioni a densità intermedia: la rappresentazione della LF mediante una
combinazione G+S è migliore di una semplice S in entrambe le bande;
 regioni ad alta densità: la LF può essere rappresentata con una semplice S;
 la LF varia in modo significativo man mano che si procede da ambienti poco
densi ad ambienti molto densi, in entrambe le bande  gli effetti
dell’ambiente del superammasso sono molto forti nelle regioni poco dense.
LF del superammasso di Shapley in banda B (sinistra) e banda R (destra) per tre diversi
ambienti:
1) densità elevata (linea nera); 2) densità intermedia (linea rossa); 3) densità bassa
(linea blu)
LF in banda R per tre diverse regioni di densità.
LF in banda B per tre diverse regioni di densità.
Dipendenza della LF dalla popolazione di galassie
 La
popolazione di galassie è stata selezionata in base al colore (B - R);
 la distribuzione delle galassie rosse nelle tre regioni a diversa densità
viene descritta meglio dalla LF totale essendo presente un avvallamento a
B ~ 17.0;
 per la popolazione blu la LF è bene rappresentata da una semplice S in
tutti gli ambienti considerati  questa popolazione non ha ancora
interagito con l’ambiente del superammasso.
LF per la popolazione di galassie rossa (cerchi aperti – linea
tratteggiata) e blu (cerchi pieni – linea continua) nei tre diversi
ambienti considerati.
Relazione “colore – magnitudine”
Il colore di una galassie è correlato alle proprietà delle popolazioni
stellari di cui è composta e al contenuto di polveri;
una galassia si dice “rossa” o “blu” a seconda che essa emetta più
radiazione, e quindi sia più luminosa, nella regione rossa o blu dello
spettro;
l'interpretazione dei colori delle galassie ellittiche è complicata
dalla così detta degenerazione età-metallicità;
seguire l’evoluzione dei colori delle galassie permette di capire
come evolvono le popolazioni stellari al loro interno, e quindi come
cambia la loro storia di formazione stellare;
Nel diagramma “colore – magnitudine” (CM) le galassie early-type seguono
una relazione ben definita, nel senso che le galassie più luminose sono
anche più rosse;
lo studio della variazione della pendenza di questa relazione a redshift
diversi potrebbe fornire utili informazioni per quanto riguarda la causa
dell’arrossamento delle galassie e rompere quindi la degenerazione “etàmetallicità”: bisognerebbe però saper distinguere gli effetti dovuti all’età
da quelli dovuti alla metallicità;
 si osserva che la pendenza resta pressoché costante fino a z ~ 1, mentre
varia il punto zero, in accordo con le previsioni dello scenario monolitico
(popolazione stellare che evolve passivamente): in ogni caso, i risultati non
escludono la possibilità del merging gerarchico come scenario di
formazione.
Relazione Mg2 - 0
Per studiare le proprietà delle popolazioni stellari delle galassie early-type
si può utilizzare l’indice di metallicità Mg2;
Mg2 è una quantità che si ricava dalle righe di assorbimento del magnesio,
facilmente visibili nello spettro ottico di una galassia ellittica: non misura
in modo diretto la quantità di metalli presenti nelle stelle, ma risulta ben
correlata con essa.
Riga del MgI
(5175)
anche per la relazione Mg2 - 0 esiste la degenerazione età –
metallicità, in quanto sia l’età che la metallicità producono effetti
simili sul colore e su Mg2;
La linea tratteggiata in figura rappresenta la relazione:
Mg2 = 0.20 log 0.
I simboli diversi si riferiscono a galassie ellittiche con diverse
proprietà cinematiche. Le galassie in cui è evidente la presenza di
stelle giovani o di età intermedia sono indicate col nome.
(Bender et al., 1993, ApJ, 411, 153)
Mg2 e 0 sono due parametri che si riferiscono alla stessa regione
centrale dello spettro (~ 2” – 3”);
Burstein et al. (1988) hanno dimostrato che esiste una relazione tra il
colore (B – V)0 e l’indice di metallicità Mg2;
poiché il colore è riferito all’intera galassia mentre l’indice Mg2 è
riferito alla regione centrale, il fatto che esista questa relazione
significa che le popolazioni stellari del centro della galassia sono
rappresentative dell’intero sistema.
la conseguenza della relazione precedente è che esiste anche una stretta
correlazione tra il colore (B – V)0 e la dispersione di velocità centrale 0.
Possibili spiegazioni e interpretazioni delle relazioni precedenti tra
proprietà delle popolazioni stellari (colore e indice Mg2) e proprietà
strutturali delle galassie ellittiche (0) in: Bender et al., 1993, ApJ,
411, 153.
Gradienti di colore
 Le galassie vicine hanno, in media, gradienti di colore negativo  le
popolazioni stellari diventano più blu andando verso l’esterno (Peletier
et al., 1990, AJ, 100, 1091; Peletier et al., 1990, AA, 233, 62);
i gradienti di colore evolvono poco col redshift  nelle galassie
ellittiche i gradienti di colore delle popolazioni stellari sono una
conseguenza dei gradienti di metallicità (Saglia et al., 2000, AA, 360,
911; Tamura & Ohta, 2000, AJ, 120, 533; La Barbera et al., 2002, ApJ,
571, 790; La Barbera et al., 2003, AA, 409, 21), anche se non è da
escludere a priori la presenza di un gradiente d’età (Saglia et al., 2000,
AA, 360, 911; La Barbera et al., 2003, AA, 409, 21);
La presenza dei gradienti di metallicità è compatibile sia con lo scenario
del “collasso monolitico” che con lo scenario del “merging gerarchico”
per quanto riguarda il processo di formazione delle galassie ellittiche;
La Barbera et al. (2004) non trovano alcun gradiente di colore
nell’ottico per l’ammasso A2163B (z ~ 0.2), mentre per i colori “ottico –
NIR” trovano un gradiente medio di -0.48  0.06  questo risultato è
difficilmente spiegabile nell’ambito dello scenario del “collasso
monolitico”, mentre trova una migliore spiegazione nell’ambito dello
scenario del “merging gerarchico”.
Popolazioni stellari
Con il termine popolazione stellare si è soliti indicare un insieme
di stelle di diversa massa ma che hanno in comune alcune
caratteristiche, come l'età (supponendo che tutte le stelle di
quella popolazione si siano formate alla stessa epoca) e la
composizione chimica.
Le galassie sono composte da stelle con proprietà fisiche differenti  la
distribuzione spettrale della luce di una galassia corrisponde a queste
differenti proprietà;
dall'evoluzione stellare sappiamo che le proprietà delle stelle dipendono,
essenzialmente, dalla loro massa  stelle di grande massa hanno una vita
breve (~ 108 anni) ed emettono la maggior parte della radiazione nella
regione blu dello spettro ( ~ 3000 - 5000 Å); viceversa, stelle di piccola
massa hanno una vita lunga (~ 1010 anni) ed emettono la maggior parte della
radiazione nella regione rossa dello spettro ( ~ 7000 - 9000 Å);
lo spettro di una galassia è la somma degli spettri delle sue stelle  le
proprietà degli spettri delle galassie si ottengono combinando gli spettri
delle stelle di diversa massa di cui sono composte, pesando il contributo
delle stelle di una data massa con il numero di queste (sintesi delle
popolazioni stellari).
Una popolazione stellare giovane è composta, principalmente, da stelle di
grande massa e di colore blu:
1) sarà caratterizzata, complessivamente, da un colore blu;
2) poiché le stelle di grande massa vivono per un breve periodo, la loro
presenza indica che la popolazione stellare di cui fanno parte è "giovane",
cioè è stata formata di recente;
3) le galassie dominate da popolazioni stellari giovani mostrano un colore blu.
Disco di galassia
a spirale.
Lo spettro a
fianco mostra
la distribuzione
spettrale di un
disco,
particolarmente
intensa
nella
regione blu.
Nelle galassie ellittiche, in cui prevale la presenza di una popolazione
stellare vecchia, lo spettro sarà dominato dalla radiazione emessa nella
regione rossa.
Galassia
ellittica
Spettro tipico
di una galassia
ellittica,
più
intenso
nella
regione rossa.
Le proprietà osservate delle galassie dipendono anche dalle proprietà
chimiche delle stelle che le compongono;
le galassie con stelle ricche di metalli, cioè di elementi piu pesanti
dell'idrogeno e dell'elio, dette galassie di "elevata metallicità",
mostrano colori rossi;
le galassie povere di metalli, dette galassie di "bassa metallicità",
mostrano colori blu;
la teoria dell'evoluzione stellare permette di calcolare le proprietà
(come il colore) di una intera popolazione stellare in funzione di
parametri quali l'età e la metallicità;
i modelli di sintesi di popolazioni stellari consentono di creare una
corrispondenza tra le proprietà fisiche (età e metallicità) delle
galassie e le caratteristiche degli spettri luminosi emessi da queste, in
particolare dei colori;
lo studio delle popolazioni stellari nelle galassie consiste nel misurare
le caratteristiche degli spettri emessi dalle galassie e, utilizzando
questa corrispondenza, derivare le proprietà fisiche delle popolazioni
stesse.
Degenerazione età - metallicità
Il colore rosso di una galassia può essere dovuto a due effetti:
1) galassia intrinsecamente più ricca di metalli;
2) galassia più vecchia.
Infatti, in una galassia “vecchia”, le stelle di seconda
generazione si sono formate da un gas arricchito di metalli, residuo
dall’esplosione delle stelle di prima generazione, e quindi sono rosse per la
metallicità. Analogamente, una galassia “giovane” le cui stelle si sono
formate da un gas arricchito di metalli sarà “rossa” per lo stesso
effetto.
il colore della popolazione stellare è determinato dal colore del punto
di “turn-off” della “sequenza principale” (MSTO);
 due popolazioni, di cui una un po' più vecchia ed una un po' più
metallica, hanno lo stesso MSTO e quindi mostrano quasi esattamente
lo stesso spettro  non è facile capire se la relazione coloremagnitudine sia dovuta ad una differenza in età o in metallicità. Per
rompere la degenerazione ci sono diverse tecniche:
Si possono osservare le galassie ellittiche lontane, nel
momento in cui erano più giovani, rivelando così in modo
diretto eventuali differenze di età:  il punto delicato
consiste
nel
confrontare
osservazioni
locali
con
osservazioni di galassie lontane;
per le galassie locali si possono utilizzare i dettagli fini degli
spettri, come i rapporti tra alcune righe particolari, che
dipendono in modo diverso da età e metallicità (indici di riga):
 i risultati però dipendono dai modelli utilizzati per
interpretare le popolazioni stellari;
si possono osservare le galassie nel vicino IR, dove gli effetti
di età e metallicità cominciano a distinguersi:  anche in
questo caso, i risultati vengono interpretati alla luce dei
modelli di popolazione stellare.
Relazioni tra parametri strutturali
Per le galassie esistono relazioni strutturali, analoghe al diagramma
HR per le stelle, che le portano ad occupare regioni limitate in un
certo spazio dei parametri.
A differenza delle stelle però queste relazioni non sono generali ma
valgono per classi limitate di galassie, e sono in genere di
interpretazione complessa.
In particolare, per le ellittiche valgono una serie di relazioni, quali
la CM e la Mg2 - 0 che, come visto, permettono di ottenere utili
informazione sulle proprietà di queste galassie, nel loro insieme.
Una relazione particolare tra parametri delle galassie ellittiche è il
così detto “Piano Fondamentale” (Dressler et al., 1987, ApJ, 313,
42; Djorgovski & Davis, 1987, ApJ, 313, 59), che definisce uno
spazio 3-D tra i seguenti osservabili: la dispersione centrale di
velocità 0, il raggio efficace re, e la brillanza superficiale e.
Poiché di questi 3 parametri solo uno (re) dipende dalla distanza,
questa relazione può essere utilizzata in modo efficace come
“indicatore di distanza”.
Queste tre quantità non si dispongono nello spazio in modo casuale,
ma definiscono un “piano sottile” che nella banda r di Gunn assume la
seguente forma (Jørgensen et al., 1996, MNRAS, 280, 167):
log Re = 1.24 log 0 - 0.82 e + ’
L’esistenza del “Piano Fondamentale” (FP) per le galassie ellittiche
può essere spiegato in modo semplice a partire dal teorema del
Viriale, che permette di ricavare il seguente “Piano Fondamentale
teorico”:
log Re = 2 log 0 - 0.4 e + log (CrCv) – log (M/L) + 
dove Cr e Cv sono due costanti di struttura adimensionali e M/L è il
rapporto “massa – luminosità” delle galassie.
Il piano teorico è leggermente diverso da quello osservato, nel senso
che tra i due piani esiste un’inclinazione meglio conosciuta col
termine di “tilt del piano fondamentale”.
Possibili spiegazioni del “tilt del FP”:
1. le galassie ellittiche sono strutture omologhe ed il rapporto
M/L è una funzione della massa M;
2. le galassie ellittiche non sono strutture omologhe
Nel caso 1., tutte le galassie ellittiche sono tra di loro simili, sia per
quanto riguarda la struttura che la cinematica, per cui i parametri Cr e
Cv sono costanti ed il “tilt” è dunque dovuto alla dipendenza del
rapporto M/L da M.
Nel caso 2., le galassie ellittiche non sono tra di loro simili, per cui i
parametri Cr e Cv non sono costanti ed a ciò è da imputare il “tilt” del
piano fondamentale. In questo caso, il rapporto M/L è una costante.
Altro aspetto importante del FP:
pur essendo un piano “sottile”, è presente una dispersione non
spiegabile esclusivamente con gli errori di misura sulle grandezze
coinvolte  questo costituisce ancora un puzzle non risolto del FP.
 Si crede che il FP sia una conseguenza dei processi di
formazione ed evoluzione delle galassie ellittiche;
 la sua origine fisica non è ancora chiara;
 se i profili di luminosità e la struttura dinamica delle
galassie ellittiche sono tra di loro simili (omologia),
allora il teorema del viriale implica che il rapporto M/L
sia una funzione di re, <e>, 0. Ma se la funzione che
lega M/L con re, <e>, 0 è unica ed è esprimibile con
una legge di potenza, allora ci si aspetta una relazione
come il piano fondamentale;
 l’eventuale processo fisico che porta a questa
relazione unica tra M/L e re, <e>, 0 non è noto;
Proiezioni del piano fondamentale:
1) Relazione di Kormendy:
(log re , <e>)
Questa relazione ci dice che
tanto più le galassie ellittiche
sono grandi e luminose, tanto
meno sono dense.
Essa dovrà essere spiegata
dalle teorie di formazione
delle galassie.
Una possibile interpretazione
è che le galassie ellittiche di
bassa luminosità si siano
formate dissipando più gas
rispetto a quanto abbiano
fatto le galassie ellittiche
giganti.
Versione originale della relazione di Kormendy (1977)
Per
una
discussione
sulle
implicazioni derivanti da una
dipendenza della pendenza da z,
si veda: La Barbera et al. (2003,
ApJ, 595, 127).
2) Relazione Faber-Jackson:
(MT , log 0)
Maggiore è la dispersione di velocità
centrale di una galassia ellittica,
maggiore è la sua luminosità:
L  04
Questa
relazione
può
essere
utilizzata
come
indicatore
di
distanza, quando viene confrontata
con la stessa relazione ottenuta per
galassie di distanza nota.
Relazione di Tully-Fisher:
Stessa relazione ottenuta per le
galassie a spirali, sostituendo alla
dispersione centrale la velocità
massima di rotazione:
L  vmax4
3) Relazione di Dressler: (Dn , 0)
 Questa relazione è equivalente alla Faber-Jackson e alla
Tully-Fisher e rappresenta il piano fondamentale visto
di “taglio”;
 si usa la correlazione tra la dispersione di velocità
centrale ed il diametro angolare dell’isofota avente una
certa brillanza superficiale: per questo motivo può
essere considerata come un miglioramento della
relazione di Faber-Jackson;
 la sua calibrazione è più difficoltosa rispetto alla TullyFisher in quanto ci sono solo poche galassie ellittiche
giganti vicine;
 questa relazione è un ulteriore esempio di come il piano
fondamentale possa essere utilizzato come indicatore di
distanza.
Il piano fondamentale come indicatore di distanza
 L’equazione:
log re =  log 0 +  <e> + 
lega una quantità che dipende linearmente dalla distanza (re)
a quantità che sono indipendenti dalla distanza (0 e <Ie> =
L/(2re2)).
 Misurando re in arcsec (e) e determinandone il valore in kpc
tramite l’equazione del piano fondamentale si determina la
distanza D della galassia con una precisione del 20% (D =
(206265 x re)/e).
 Una stima indipendente della distanza si ottiene con la legge
di Hubble: DH = cz/H0.
 La differenza tra la velocità di recessione e D, espressa in
km/s, ci fornisce la velocità peculiare:
vpec = cz - D/H0
I coefficienti del piano fondamentale:
Per un sistema in equilibrio vale il teorema del viriale:
2E + U = 0
L’energia cinetica per unità di massa per una galassia ellittica
vale: E  02.
L’energia potenziale gravitazionale per unità di massa per una
galassia ellittica vale: U  -GM/r.
Per il teorema del viriale deve dunque valere una relazione del
tipo: 02  GM/r
Essendo:
L = c1 <Ie> re
M = c2 re 02
L
c1 <Ie>
= c  2 re
2
0
M
re = c2 1 02 1
c1 M/L
<Ie>
c1 e c2 sono due costanti strutturali che dipendono dalla
densità e dalla dinamica della galassia
Se: c2/c1  Lb
(b = 0  strutture omologhe  tutte le galassie
ellittiche hanno la stessa struttura dinamica)
Se:
(a = 0  tutte le galassie ellittiche hanno le
stesse popolazioni medie)
M/L  La
re  Lb L-a 02 <Ie>-1 = L(b-a) 02 <Ie>-1  (re2 <Ie>)
(b-a)
02 <Ie>-1 = re2(b-a) <Ie>(b-a) 02 <Ie>-1
re(1+2a-2b)  <Ie>(b-a -1) 02  (1+2a-2b) log re  2 log 0 + (b-a-1) log <Ie>
log re  [2/(1+2a-2b)] log 0 + [(b-a-1)/(1+2a-2b)] log <Ie>
Posto:  = [2/(1+2a-2b)]
 = [(b-a-1)/(1+2a-2b)]
i valori:  = 1.25 e  = - 0.82 si ottengono per a = 0.3 e b = 0.
Fine