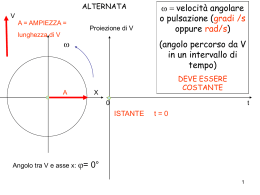
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
(angolo percorso da V
in un intervallo di
tempo)
w
A
w = velocità angolare
o pulsazione (gradi /s
oppure rad/s)
DEVE ESSERE
COSTANTE
X
0
t
ISTANTE
Angolo tra V e asse x: =
t=0
0°
1
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
X
=30°
0
t
t1
ISTANTE
Angolo tra V e asse x :
w=30/ t1
t = t1
= 30°
2
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
X
=60°
0
t
t1
t2
ISTANTE
Angolo tra V e asse x : =
w=60/ t2
t = t2
60°
3
ALTERNATA
V
Proiezione di V
A = AMPIEZZA =
lunghezza di V
A = AMPIEZZA =
w
lunghezza di V
X
=90°
0
t
t1
t2
t3 = T/4
ISTANTE
Angolo tra V e asse x : =
t = t3 = T/4
90°
w=90/ t3= 90°/(T/4)=360°/T= 2p/T
4
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
X
=120°
0
t
t1
t2
t3 = T/4
t4
ISTANTE
Angolo tra V e asse x : =
w=120/ t4
t = t4
120°
5
ALTERNATA
V
Proiezione di V
A = AMPIEZZA =
lunghezza di V
w
=150°
X
0
t
t1
Angolo tra V e asse x : =
w=150/ t5
t2
t3 = T/4
t4
t5
ISTANTE
t = t5
150°
6
ALTERNATA
V
Proiezione di V
A = AMPIEZZA =
lunghezza di V
Semionda positiva
w
=180°
X
0
t
t1
t2
t3 = T/4
t4
ISTANTE
Angolo tra V e asse x : =
t5
t6 = T/2
t = t6 = T/2
180°
w=180/ t1=180°/(T/2)=360°/T= 2p/T
7
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
=210°
X
t7
t
t6
ISTANTE
Angolo tra V e asse x : =
w=210/ t7
t = t7
210°
8
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
=240°
t7
X
t8
t
t6
ISTANTE
Angolo tra V e asse x : =
w=240/ t8
t = t8
240°
9
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
AMPIEZZA =
lunghezza di V
=270°
t7
X
t8
t9 = 3T/4
t
t6
ISTANTE
Angolo tra V e asse x : =
t = t9 = 3T/4
270°
w=270/ t9=270°/(3T/4)=360°/T = 2p/T
10
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
=300°
t7
X
t8
t9 = 3T/4
t10
t
t6
ISTANTE
Angolo tra V e asse x : =
w=300/ t10
t = t10
300°
11
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
=330°
t7
X
t8
t9 = 3T/4
t10
t11
t
t6
ISTANTE
Angolo tra V e asse x : =
w=330/ t11
t = t11
330°
12
ALTERNATA
V
A = AMPIEZZA =
lunghezza di V
Proiezione di V
w
t7
X
=360°
Angolo tra V e asse x : =
w =2p/T
t8
t9 = 3T/4
ISTANTE
t10
t11
t = t12= T
t12 = T
t
t6
360° =2p
Semionda negativa
13
Proiezione di
V
RIEPILOGO
t9 = 3T/4
t7
t1
t2
t3 = T/4
t4
LE DUE SEMIONDE
(POSITIVA E NEGATIVA)
INSIEME FORMANO
UNA ALTERNANZA
t5
t8
t12 = T
t10
t11
t6 = T/2
w =2p/T
T = PERIODO
T = è l’intervallo di tempo che occorre al
vettore V per effettuare un giro
completo (2p) del cerchio
trigonometrico
T = è anche l’intervallo di tempo che
occorre per descrivere le semionde
14
LA FREQUENZA
w =2p/T
t
ESEMPIO: Supponiamo che questo intervallo di tempo duri 1
secondo;
Domanda: quante alternanze vi sono contenute?
Risposta: 8
DEFINIZIONE DI FREQUENZA:
è il numero di alternanze contenute in 1 secondo
UNITA’ DI MISURA DELLA FREQUENZA: HERTZ (Hz)
Nell’esempio precedente la frequenza è 8 Hz.
15
ESERCIZI
1.
Una sinusoide presenta un periodo T = 1 ms. Quante
alternanze ci sono in un secondo (cioè la frequenza)?
Soluzione: siccome un secondo è formato da 1000 ms,
vuol dire che in un secondo entrano 1000 alternanze.
Quindi la frequenza vale f = 1000 Hz.
2. Una sinusoide presenta una frequenza di 50 Hz.
Quanto vale il suo periodo T?
Soluzione: 50 Hz significa che la sinusoide presenta 50
alternanze in 1 secondo. Quindi per conoscere il
periodo T occorre dividere l’intervallo di 1 secondo
in 50 parti. T = 1/50 = 0,02 s = 0,02*1000 ms = 20
ms.
16
FORMULE TRA PERIODO E FREQUENZA
Nel secondo esercizio appena eseguito
abbiamo ricavato con un semplice
ragionamento una relazione tra periodo
“T” e frequenza “f”.
Possiamo generalizzarla.
• T = 1/f
• f = 1/T
• ATTENZIONE: se T è in secondi f è in
Hertz
17
FORMULE TRA PERIODO, FREQUENZA E PULSAZIONE
Troviamo ora un’ultima formula.
Sappiamo già che: w =2p / T (rad/s)
Siccome abbiamo ricavato che: T = 1/f, possiamo
sostituire questa formula in quella della
pulsazione. Otteniamo quindi:
2p
2p
2p  f
w=
=
=
= 2p  f
T
1
1
 
f 
18
FASE INIZIALE: (il vettore V è disegnato nella sua posizione all’istante t = 0)
X
 = 30°
X
 = 60°
X
 = 90°
In queste tre figure
abbiamo il vettore V
in posizioni angolari
diversi all’istante
t=0.
Nella prima figura il
vettore V forma un
angolo iniziale di
30°, nella seconda
un angolo di 60°,
nella terza un
angolo di 90°.
Le tre sinusoidi
iniziano da un
valore che non è
zero, ma deve
essere calcolato con
la trigonometria.
19
FASE INIZIALE: (il vettore V è disegnato nella sua posizione all’istante t=0)
X
 = 180°
In queste ultime due
figure abbiamo il
vettore V che forma
un angolo iniziale di
180° ed uno di 270°.
X
 = 270°
DEFINIZIONE: l’angolo  che il vettore V forma con l’asse x all’istante t =0, è
chiamato FASE INIZIALE
20
FORMULA DELLE SINUSOIDI
In questi ragionamenti
supponiamo che V abbia
una lunghezza A = 1
0,5
0,866
X
X
Consideriamo ora alcune situazioni.
1. Quando il vettore V ha una fase iniziale  = 0° ,
la sua proiezione sull’asse y è zero.
 = 30°
2. Quando il vettore V ha una fase iniziale  = 30° ,
la sua proiezione sull’asse y è sen(30°) = 0,5.
 = 60°
3. Quando il vettore V ha una fase iniziale  = 60° ,
la sua proiezione sull’asse y è sen(60°) = 0,866.
4. Quando il vettore V ha una fase iniziale  = 90° ,
la sua proiezione sull’asse y è sen(90°) = 1.
21
FORMULA DELLE SINUSOIDI
t=0
Per ricavare la formula supponiamo che la
0,5
 = 30°
X
fase iniziale sia 
= 30°.
Supponiamo che il vettore V abbia una
pulsazione w
= 10°/s.
Ciò significa che il vettore percorre un
angolo di 10° al secondo.
Ci possiamo ora chiedere quale sia
l’angolo che forma il vettore V (con
l’asse x) ad un istante qualsiasi.
0,64
X
 = 40°
1. All’istante t=1 s l’angolo  sarà 30° +
10° * 1 = 40°. Quindi possiamo
calcolare la proiezione di V sull’asse y:
sen(40°) = 0,64
Continua ./.
22
FORMULA DELLE SINUSOIDI
0,77
X
0,866
X
 = 50°
2. All’istante t=2 s l’angolo  sarà 30° + 10° * 2 =
50°. Quindi possiamo calcolare la proiezione di
V sull’asse y: sen(50°) = 0,77
 = 60°
3. All’istante t=3 s l’angolo  sarà 30° + 10° * 3 =
60°. Quindi possiamo calcolare la proiezione di
V sull’asse y: sen(50°) = 0,866.
Possiamo trarre alcune conclusioni generali:
1. dopo un intervallo di tempo “t” l’angolo  che forma il vettore V con l’asse X si
calcola con la formula:  = ( 
+ w * t)
2. Il valore della proiezione di V sull’asse y si calcola con la formula conosciuta
dalla trigonometria: sen ()
= sen (  + w * t)
23
FORMULA DELLE SINUSOIDI
I ragionamenti precedenti sono stati fatti considerando che la lunghezza del
vettore V sia di valore A = 1.
Adesso consideriamo che il vettore abbia una lunghezza qualsiasi, cioè A.
La formula che abbiamo trovato per rappresentare una sinusoide si può scrivere
nella forma più generale possibile:
y = A * sen (  + w * t)
Ricordiamo le altre formule:
T = 1/f
f = 1/T
2p
w=
= 2p  f
T
24
Unità di misura degli angoli
Il radiante (simbolo rad) è l'unità di misura degli angoli del
Sistema internazionale di unità di misura. Tale misura
rappresenta il rapporto tra la lunghezza di un arco di
circonferenza spazzato dall'angolo, diviso per la lunghezza
del raggio di tale circonferenza.
25
Unità di misura degli angoli
Utilità della scelta del radiante
La misura del radiante consente di
avere formule trigonometriche
molto più semplici di quelle che si
avrebbero adottando come unità
di misura per gli angoli i gradi
sessagesimali.
Formule di conversione:
1 rad = 57,29 gradi
1 grado = 0,0174 rad
gradi
radianti
0
0
15
(1/12) π
30
(1/6) π
45
(1/4) π
60
(1/3) π
90
(1/2) π
120
(2/3) π
135
(3/4) π
150
(5/6) π
180
π
210
(7/6) π
225
(5/4) π
240
(4/3) π
270
(3/2) π
300
(5/3) π
315
(7/4) π
330
(11/6) π
360
2π
26
ESERCIZI SULLE SINUSOIDI
1.
Una sinusoide ha la frequenza di 100 Hz, l’ampiezza A=5, la
fase iniziale =15°. a) Quanto vale T ? b) Quanto vale w?
c)Quale angolo  è formato dal vettore V con l’asse “x” dopo
un intervallo t = 1 ms? d) Quale valore assume la sinusoide
dopo che è trascorso intervallo t = 1 ms?
RISPOSTA: a)T = 1/f = 1/100 = 0,01 s = 10 ms. b) w = 2pf =
6,28*100 = 628 rad/s. c) = + w*t (occorre trasformare i
gradi in radianti  = 15° = (1/12) π), = (1/12) π + 628*0,001 =
0,2617+0,628 = 0,8897 rad = 0,8897 * 57,29 = 50,97 °.
d) y = A * sen (
 + w * t) = 5*sen (0,8897) = 5*sen(50,97) =
5*0,7768 = 3,884
27
VALORE MEDIO DELLE SINUSOIDI
+2
+1
+3
+2
+1
T
-1
-2
-1
-3
-2
Quando si parla di valore medio si intende una operazione matematica del tipo:
(A+B) / 2. Nel caso di una sinusoide si deve considerare un intervallo di tempo pari
al periodo T e al suo interno si deve fare l’operazione precedente ripetuta per tutti i
valori che la sinusoide stessa assume. Infatti si tratta di sommare i numeri che
sono rappresentati nel grafico aventi lo stesso colore e poi dividere per 2. È
evidente che le somme risulteranno tutte uguali a zero. Infatti: (+1-1)/2 =0; (+2-2)/2
=0; (+3-3)/2 =0; ecc.
La conclusione di questo ragionamento è che una sinusoide ha
VALORE MEDIO = 0
28
SINUSOIDI CON VALORE MEDIO DIVERSO DA ZERO
+3
+2
+4
+3
+2
+1
+1
+1
0
0
0
-1
-2
-1
In questo secondo caso la sinusoide è stata traslata verso l’alto (di +1). Il risultato del
calcolo del valore medio ora non è più zero.
Un calcolo approssimativo ci fornisce il seguente risultato:
(+1+1)/2=+1; (+2+0)/2=+1; (+3-1)/2=+1; (+4-2)/2=+1; (+3-1)/2=+1; (+2+0)/2=+1;
In effetti un calcolo matematico più rigoroso (che però va oltre le conoscenze di
questo corso) ci fornisce lo stesso risultato, cioè +1.
Si può concludere che il valore medio di una sinusoide è pari al valore “n”(positivo o
negativo) di cui è stata traslata verso l’alto o verso il basso.
29
T
SINUSOIDI CON VALORE MEDIO DIVERSO DA ZERO
Un calcolo più preciso del valore medio si può fare graficamente. Occorre calcolare
la superficie colorata. Per evitare calcoli troppo complicati si ricorre ad operazioni
grafiche controllabili visivamente.
30
SINUSOIDI CON VALORE MEDIO DIVERSO DA ZERO
1
2
In questa diapositiva le zone colorate di verde sono uguali ma di segno opposto e
quindi la loro media è zero:quindi possiamo cancellarle. Le zone colorate di giallo
invece sono entrambe positive e di uguale superficie. Possiamo quindi “tagliare”
la zona
1 “incollarla” nella zona 2. Si ottiene quindi la figura successiva.
31
SINUSOIDI CON VALORE MEDIO DIVERSO DA ZERO
Come si nota dalla figura, dopo avere eliminato le parti positive e negative, ma
di uguale valore, resta una parte del grafico originale che è costante. La
conclusione di tutto il ragionamento grafico è che una sinusoide traslata verso
l’alto o verso il basso di “n” ha valore medio proprio uguale ad “n”. Nel nostro
32
esempio quindi il valore medio è +1.
VALORE EFFICACE DI UNA SINUSOIDE
Il valore medio appena discusso ha poca importanza pratica. Si studia poiché è
necessario per comprendere il nuovo valore chiamato “EFFICACE”. Questo
nuovo parametro è invece fondamentale nello studio delle grandezze elettriche
alternate che inizieremo tra poco. La sua importanza sarà chiara più avanti nel
corso. Possiamo anticipare che con questo “valore efficace” potremo trattare
l’alternata come se fosse una “continua”, con una facilitazione dei calcoli e dei
ragionamenti.
Anche in questo caso tratteremo l’argomento in modo grafico, poiché
matematicamente risulterebbe al di fuori della portata delle cognizioni attuali della
classe.
Supporremo di avere una sinusoide come quella utilizzata per il calcolo del
valore medio.
La sinusoide ha la seguente espressione:
Y = 3*sen(2*p * f * t)
La cosa importante è il valore di ampiezza che vale 3. Si tratta ovviamente di un
esempio, quindi in seguito il valore numerico 3 sarà sostituito dal valore generico
A.
33
VALORE EFFICACE DI UNA SINUSOIDE
Per determinare il “valore efficace” di una sinusoide occorre procede come indicato di
seguito.
1.
Calcolare il quadrato di una sinusoide;
2.
Calcolare il valore medio del quadrato appena calcolato.
3.
Fare la radice quadrata del valore medio calcolato al punto 2.
Consideriamo il punto 1.
Cosa significa calcolare il quadrato di una sinusoide?
Supponiamo di considerare l’espressione precedente:
Y = 3*sen(2*p * f * t)
Il suo quadrato si calcola matematicamente in questo modo:
Y2 = [3*sen(2*p * f * t)]2 = 9*[sen(2*p * f * t)]2
Invece di effettuare il calcolo matematicamente, lo effettueremo graficamente.
Il grafico risultante dovrà avere un valore massimo uguale a 9 e dovrà essere
sempre di valore positivo (per effetto dell’operazione di elevazione al quadrato)
Vediamo graficamente il risultato dell’operazione di elevazione al quadrato di una
sinusoide.
34
VALORE EFFICACE DI UNA SINUSOIDE
4
3
2
1
0
-1
0
1
2
3
4
5
6
7
Questa è la sinusoide
originale (di ampiezza = 3)
-2
-3
-4
Questo è il risultato
della operazione di
elevazione al quadrato
(notare ampiezza = 9
e valori tutti positivi,
cioè la curva sta tutta
sopra l’asse x).
10
9
8
7
6
5
4
3
2
1
0
0
1
2
3
4
5
6
7
Infine si nota anche un
raddoppio della
frequenza.
35
VALORE EFFICACE DI UNA SINUSOIDE
10
9
8
4,5
7
6
5
4
3
2
1
0
0
1
2
3
4
5
6
7
Passiamo adesso a considerare il punto 2.
Una prima osservazione su questo grafico ci dice che il valore medio è pari a 4,5
(la metà dell’ampiezza che è 9). Questa osservazione si può verificare come è
stato già fatto in precedenza, quando abbiamo parlato del valore medio di una
sinusoide.
36
VALORE EFFICACE DI UNA SINUSOIDE
Anche in questo caso possiamo ripetere le stesse considerazioni fatte in
precedenza sul valore medio e troveremo che esso è proprio 4,5.
Successivamente vedremo come calcolare la superficie colorata in blu in
modo semplice e quindi calcolare il valore efficace.
37
VALORE EFFICACE DI UNA SINUSOIDE
Da questa figura si comprende perché il valore medio è 4,5. Basta spostare le parti
di colore uguale come indicato e avremo il risultato della figura successiva.
Inoltre si nota facilmente che la superficie della curva originale (in blu) non cambia.
38
VALORE EFFICACE DI UNA SINUSOIDE
Abbiamo dimostrato che il valore medio del quadrato di una sinusoide è pari alla
metà della sua ampiezza. In questo caso l’ampiezza è (3)2 = 9 e quindi il valore
medio è 4,5. Più in generale possiamo stabilire la seguente formula:
Dato che A è l’ampiezza della sinusoide, il valore medio del quadrato di una
sinusoide è (A)2 / 2.
Notiamo da questa figura che la superficie è rimasta inalterata. Adesso però si tratta 39
di calcolare l’area di un rettangolo, molto più semplice rispetto a prima.
VALORE EFFICACE DI UNA SINUSOIDE
Infine consideriamo il punto 3.
Ricordiamo che abbiamo fatto il quadrato di una sinusoide, poi abbiamo
calcolato il valore medio della nuova funzione, ora dobbiamo fare la radice
quadrata di questo valore medio, per ritornare alla sinusoide iniziale.
Quindi il valore efficace di una sinusoide è ottenuta con la formula seguente:
V
EFF
A
A
A2
=
=

 0,707  A
2
2 1,414
40
VALORE EFFICACE DI UNA SINUSOIDE
Applichiamo la formula appena trovata alla sinusoide da cui eravamo partiti.
Y = 3*sen(2*p * f * t)
L’ampiezza è A = 3.
Il valore efficace si calcola:
VEFF = 0,707*A = 0,707*3 = 2,121
2,121
3
2,7
2,4
2,1
1,8
1,5
1,2
0,9
0,6
0,3
0
-0,3
-0,6 0
-0,9
-1,2
-1,5
-1,8
-2,1
-2,4
-2,7
-3
1
2
3
4
5
6
7
41
SOMME E DIFFERENZE CON LE SINUSOIDI
In elettrotecnica è frequente effettuare somme e differenze tra sinusoidi avente
la stessa frequenza “f”. Il calcolo con le regole della trigonometria è lungo
e spesso complesso, quindi occorre trovare una tecnica rapida e
semplice.
Facciamo un esempio:
1.
Y1 = 3*sen(2*p * f * t) = 3*sen(2*p * 50 * t)
2.
Y2 = 4*sen(2*p * f * t) = 4*sen(2*p * 50 * t)
Abbiamo due sinusoidi con la stessa frequenza f = 50 Hz (deve essere sempre
così !!), la stessa fase iniziale  = 0, ampiezze diverse A1 = 3 ed A2 = 4.
Calcoliamo ora la somma e la differenza delle due sinusoidi:
YS = Y1 + Y2
YD = Y1 - Y2
Nella prossima diapositiva visualizzeremo i risultati ottenuti con EXCEL, senza calcolare
matematicamente in modo diretto le formule.
Vedremo nello stesso istante ( t = 0,005 s) l’ampiezza della nuova curva e trarremo
conclusioni.
42
SOMMA TRA SINUSOIDI
Y1
3
Y2
4
4
6
3
4
2
2
1
t
0
-1 0
0,005
0,01
0,015
0,02
0,025
t
0
-2 0
-2
-4
-3
-6
0,005
0,01
0,015
0,02
0,025
-4
Ys
7=3+4
8
6
4
2
0
-2 0
-4
-6
-8
t
0,005
0,01
0,015
0,02
0,025
La somma è
ancora una
sinusoide,
avente la
stessa
frequenza e
avente
come
ampiezza la
somma
delle
ampiezze.
43
DIFFERENZA TRA SINUSOIDI
+1 = - 3 - (-4)
Yd
1,5
1
0,5
t
0
-0,5 0
0,005
0,01
0,015
0,02
0,025
-1
-1,5
-1=3 - 4
La differenza è ancora una sinusoide, avente la stessa frequenza e avente
come ampiezza la differenza delle ampiezze.
44
RIEPILOGO DELLA SOMMA E DIFFERENZA TRA SINUSOIDI
Ys
8
Y2
6
Y1
4
2
t
0
-2
0
0,005
0,01
0,015
0,02
0,025
-4
-6
-8
Yd = Y1 – Y2
Conclusioni: somme e differenze tra sinusoidi isofrequenziali, sono ancora
sinusoidi di stessa frequenza, ma con ampiezze diverse (o somma o differenze tra
le ampiezze originarie). La fase iniziale, supposta zero, resta ancora zero.
NOTA: la differenza Yd si poteva ottenere anche facendo Yd = Y2 – Y1, ma la
sinusoide risultante sarebbe stata ribaltata (sfasata di 180°).
45
SOMMA E DIFFERENZA TRA SINUSOIDI: METODO VETTORIALE
La tecnica grafica non è utilizzabile praticamente in elettrotecnica. Il metodo
vettoriale è invece molto più facile e veloce. Vediamo in cosa consiste.
VETTORI IN FASE
Y1 = 3
Y2 = 4
Come già descritto in precedenza, ogni vettore
rotante descrive una sinusoide. Quindi
utilizziamo i vettori sommandoli o sottraendoli
tra loro per ottenere le sinusoidi corrispondenti.
Di conseguenza possiamo sostituire le
operazioni trigonometriche con operazioni
vettoriali.
YS = 3+4 = 7
YD = -1
46
ESEMPI DI CALCOLO VETTORIALE
Nei seguenti esempi tratteremo alcuni casi notevoli di somma o differenza tra vettori e
successivamente tracceremo le sinusoidi corrispondenti.
VETTORI IN QUADRATURA (1° caso)
Y2=1
YS = ?
Y1 ed Y2 sono due vettori sfasati di 90°
(si dicono in quadratura), e la loro
somma YS avrà un modulo ed una fase
calcolati di seguito.

Y1=2
y
S
=y y
1
2
modulo della somma =
y
= y 1  y 2 = 12  22 = 5 = 2,236
S
y2
1
fase della somma =  = arctg ( ) = arctg ( ) = arctg (0,5) = 26,56
y1
2
2
2
47
CORRISPONDENZA TRA VETTORI E SINUSOIDI
Y2=1
Y1
YS = 2,236
3
 =26,56°
2
1
t
Y1=2
0
-1 0
0,005
0,01
0,015
0,02
0,025
-2
-3
Ys
2,236
3
2
Y2
1
1,5
t
0
1
-1 0
0,5
t
0
-0,5
0
0,005
0,01
0,015
0,02
0,025
0,005
0,01
0,015
0,02
0,025
-2
-3
-1
-1,5
Confrontare i vettori con le rispettive sinusoidi e riconoscere la
corrispondenza tra ampiezze e tra le fasi iniziali.
48
ESEMPI DI CALCOLO VETTORIALE
VETTORI IN QUADRATURA (2° caso)
Y1
2,5
2
1,5
1
0,5
0
-0,5 0
-1
-1,5
-2
-2,5
Y1=2
 = - 26,56°
t
0,005
0,01
0,015
0,02
Y2=1
0,025
YS = 2,236
Ys
Y2
3
1,5
2
1
1
0,5
t
0
-0,5 0
-1
-1,5
0,005
0,01
0,015
0,02
0,025
t
0
-1 0
0,005
0,01
0,015
0,02
0,025
-2
-3
Anche ora confrontare i vettori con le rispettive sinusoidi e riconoscere la
corrispondenza tra ampiezze e tra le fasi iniziali.
49
ESEMPI DI CALCOLO VETTORIALE
VETTORI IN OPPOSIZIONE DI FASE
Y2= 1
Y1
 = 180°
2,5
2
1,5
1
0,5
0
-0,5 0
-1
-1,5
-2
-2,5
Y1=2
YS = Y1 - Y2
YS = 1
t
0,005
0,01
Ys
0,02
0,025
Y2
1,5
1,5
1
1
0,5
0,5
t
0
-0,5 0
0,015
0,005
0,01
0,015
0,02
0,025
t
0
-0,5 0
-1
-1
-1,5
-1,5
0,005
0,01
0,015
0,02
0,025
50
CONCLUSIONI
Al calcolo tra sinusoidi aventi la stessa
frequenza (isofrequenziali), si sostituisce il
calcolo tra vettori, più facile e veloce.
Per il calcolo tra vettori si utilizzano le
tecniche già studiate con i numeri
complessi.
51