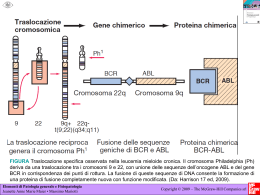
PROBLEMI STRUTTURALI
NELL’INGEGNERIA DELLE DIGHE
Progetti PRIN 2004-2006
Unità di Ricerca:
Politecnici di Milano e di Torino
Università di Padova
Roma 1
Trento
Trieste
Elenco delle pubblicazioni ottenibile da ItCOLD via e-mail ([email protected])
Unità di Ricerca Milano - Politecnico
R. Ardito, G. Bolzon, G. Cocchetti, C. Comi, R. Fedele,
A. Ghisi, G. Maier (Coordinatore), S. Mariani, U. Perego
TEMI dei PRIN 2004-2006
I - Diagnosi locale con martinetti piatti
II - Diagnosi globale con carico idrostatico stagionale: identificazione di rigidezze come indici di danno
III - Caratterizzazione meccanica di geomembrane con “membranometro”
IV - Modellazione costitutiva anelastica del cls e dei processi di danneggiamento
V - Calcolo a rottura generalizzato, anche con diffuse fessure sature
VI - Diagnosi globale con carico dinamico (collaborazione con UdR Trento e Trieste,
che riferiscono a parte)
Pubblicazioni citate nel Sommario, ottenibili per e-mail ([email protected])
ACCADEMIA NAZIONALE DEI LINCEI
CONVEGNO SU PROBLEMI STRUTTURALI
NELL’INGEGNERIA DELLE DIGHE
Roma, 12 e 13 aprile 2007
Riassunto delle presentazioni
Premessa. - Questa sessione è dedicata a presentazioni delle ricerche svolte con il supporto del MIUR negli anni 2004-2006 in sei
università italiane. Le presentazioni sono tenute dai Coordinatori delle Unità di Ricerca (UdR) dei PRIN e riguardano contributi
accademici all’innovazione nell’ingegneria strutturale delle dighe in calcestruzzo. Altri contributi e vari dettagli sui temi trattati in
questa Sessione e su altri risultati emersi da tali PRIN sono reperibili nelle pubblicazioni citate nell’elenco bibliografico già diffuso
per posta elettronica dall’ITCOLD e disponibile sul suo sito.L’auspicabile trasferimento di risultati della ricerca tecnico-scientifica
agli ambienti della pratica ingegneristica è scopo primario di questo Convegno Linceo e del precedente (febbraio 2004); è stato
anche lo scopo di numerose comunicazioni a congressi e dell’attiva partecipazione di due UdR al Network europeo sul tema
“Integrity Assessment of Large Dams” (IALAD) conclusosi all’inizio dell’anno scorso. Questa comunicazione brevemente
sintetizza i risultati che si ritengono di maggiore interesse applicativo tra quelli conseguiti dall’UdR del Politecnico di Milano, e
tende ad evidenziarne la potenziale utilità pratica raggiungibile con future collaborazioni tra università ed industrie. Dettagli sulle
ricerche svolte nel 2004 sono reperibili nelle pubblicazioni qui citate e in quelle in preparazione che saranno specificate tramite
l’ITCOLD.
Metodi di diagnosi globale. - Problematica attualmente prioritaria in Europa per ovvia incisività socio-economica concerne il
diffuso degrado delle dighe esistenti (dovuto a lenti processi chimico-fisici nel calcestruzzo e/o a carichi eccezionali sismici o da
piena) e gli eventuali interventi di ripristino. La metodologia diagnostica quasi-statica studiata dalla UdR in precedenti PRIN
presentava le seguenti peculiarità: carico per variazione “rapida” (circa una settimana) del livello d’invaso; misure di spostamenti
anche mediante radar; modellazione per elementi finiti; analisi inversa per l’identificazione deterministica dei moduli elastici quali
indici di danno strutturale nelle varie zone della diga. Nell’ambito del recente PRIN sono state indagate le innovazioni seguenti,
economicamente vantaggiose, [1] [5] [7]: impiego di economiche variazioni di invaso stagionali; conseguente messa in conto degli
effetti termici sfruttandone la periodicità stagionale mediante sviluppi in serie di Fourier e basandosi su misure termometriche
interne; impiego di reti neurali; identificazione stocastica con approcci Monte Carlo e bayesiano. Alla tradizionale diagnostica con
eccitazione dinamica mediante vibrodine e con misure accelerometriche, sono stati apportati i seguenti ampiamenti metodologici
in collaborazione con le UdR di Trento e Trieste (i cui Coordinatori riferiscono nelle loro comunicazioni): per il preliminare
calcolo delle “masse aggiunte” economico impiego del metodo degli elementi di contorno, in particolare nella versione simmetrica
“alla Galerkin”; messa in conto delle non-linearità dovute a giunti; identificazione stocastica sequenziale dei parametri elastici di
danno mediante filtro di Kalman nella versione più recente detta “unscented”.
Riassunto delle presentazioni
Metodi di diagnosi locale. - Da decenni si effettuano esperimenti intesi cogliere localmente proprietà meccaniche del calcestruzzo
di dighe suscettibili di degrado. Con riferimento alla tradizionale strumentazione dei martinetti piatti, gli studi condotti nella UdR
di Milano hanno sviluppato un procedimento le cui peculiarità innovative si possono così delineare, [4] [6]: (a) le stime ottenibili
riguardano non solo due moduli di Young e due tensioni normali, come nella prassi attuale, ma anche modulo di elasticità e
tensione tangenziali, resistenze a compressione e a trazione ed energia di frattura; (b) simulazioni delle prove ed analisi inverse
sono confinate ad una fase preparatoria da svolgere una tantum in laboratorio numerico per l’addestramento di reti neurali
artificiali da impiegare per uso ripetuto in situ. Il metodo concepito e numericamente validato nella ricerca potrebbe comportare
notevoli vantaggi in pratica dopo marginali modifiche richieste nell’apparecchiatura sperimentale. Per diagnosi locali in profondità
atte a fornire lo stesso insieme di dati utili alla progettazione di eventuali interventi, è stato concepito e numericamente convalidato
un metodo diagnostico detto “dilatometrico dei due fori”, [7] [8]. Tale metodo, sostanzialmente non distruttivo, è fondato come il
precedente sull’analisi inversa e su reti neurali per il suo impiego di routine autonomo ed economico in situ, ma richiederebbe
alcune non marginali varianti nella strumentazione attualmente disponibile.
Simulazione degli effetti della reazione alcali-aggregati (AAR) e modellazione costitutiva. - Nell’ambito del PRIN più recente le
ricerche nella UdR di Milano sui modelli costitutivi, sia di interfaccia che di materiale, si sono focalizzate sui fenomeni di
danneggiamento e frattura, [2] [3] [9]. Inoltre è stato sviluppato un nuovo modello accoppiato chemio – elasto – danno per la
simulazione ad elementi finiti della lenta reazione tra gli alcali presenti nella pasta cementizia e gli aggregati e delle sue
conseguenze strutturali. In molte dighe esistenti da qualche decennio tale reazione può avere prodotto gel espansivo nei pori e
fessurazione diffusa e conseguenti autotensioni e perdita di resistenza e rigidezza, cioè i danni la cui diagnosi è il tema degli studi
menzionati in precedenza.
Altre ricerche svolte nella UdR di Milano nel periodo 2004-2006. - Membrane per impermeabilizzazione di dighe in terra e in
calcestruzzo vengono di solito sottoposte a prove di scoppio. Uno studio tutt’ora in corso nella UdR ha dimostrato che
“scoppiometro” abbinato a profilometro laser e connesso con analisi inversa o con rete neurale “addestrata” con analisi diretta,
consente di determinare economicamente e rapidamente proprietà elastiche e plastiche delle geomembrane. Un prototipo della
nuova attrezzatura sperimentale detta “membranometro” è stato realizzato in collaborazione col Dipartimento di Meccanica del
Politecnico. Il calcolo a rottura classico fondato su massimizzazione del fattore di carico sotto vincoli di equilibrio e di
ammissibilità plastica offre vantaggi di semplicità concettuale e computazionale, ma soffre delle note limitazioni alla “plasticità
perfetta”. Tali limitazioni sono in gran parte superate dal nuovo metodo diretto (“analisi limite generalizzata”) sviluppato nel
recente PRIN e caratterizzato dalle seguenti circostanze: “linearizzazione a tratti” del modello olonomo di elasto-plasticità o poroplasticità a saturazione totale; aggiunta di vincoli di congruenza e costitutivi; ricorso a programmazione matematica con vincoli di
complementarietà (MPEC) e relativi algoritmi di ottimizzazione non convessa.
[1] Ardito R., Cocchetti G., "Statistical approach to damage diagnosis of concrete dams by radar monitoring", Engineering Structures,
vol.28, 2036-2045, 2006.
[2] Benallal, A., Comi, C., “On interfacial properties in gradient damaging continua”, C.R. Mècanique, vol.333, 319-324, 2005.
[3] Comi, C., Mariani, S. and Perego, U., “An extended FE strategy for transition from continuum damage to mode I cohesive crack
propagation”, International Journal of Numerical and Analytical Methods in Geomechanics, vol.31(2), 213-238, 2007.
[4] Fedele, R., Maier, G., Miller, B., “Identification of elastic stiffness and local stresses in concrete dams by in situ tests and neural
networks”, Structure and Infrastructure Engineering, vol. 1(3), 165-180, 2005.
[5] Fedele, R., Maier, G., Miller, B., “Health assessment of concrete dams by overall inverse analyses and neural networks”, Int. J. of
Fracture, vol. 137, 151-172, 2006.
[6] Fedele, R., Maier, G., “Flat jack tests and inverse analysis for the identification of stress states and elastic properties in concrete dams”,
Meccanica, 2007 (in stampa).
[7] Maier, G., Ardito, R., Fedele, R., “Inverse analyses problems in structural engineering of concrete dams”, SemiPlenary Lecture, World
Congress of Computational Mechanics (WCCM VI), Beijing, in: Z. H. Yao, M. W. Yuan and W. X. Zhong Eds., Computational Mechanics,
Springer, 97-107, 2005.
[8] Maier, G., Bocciarelli, M., Bolzon, G., Fedele, R., “Inverse analyses in fracture mechanics”, Int. J. of Fracture, vol. 138, 47-73, 2006.
[9] Puntel, E., Bolzon, G., Saouma, V.E., “Fracture mechanics based model for joints under cyclic loading”, Journal of Engineering
Mechanics, vol.132, 1151-1159, 2006.
Giulio Maier
Dipartimento di Ingegneria Strutturale, Politecnico di Milano
e-mail: [email protected]
I – DIAGNOSI LOCALE CON MARTINETTI PIATTI
NOVITÀ
 disposizione dei tagli
 simulazione
 analisi inversa con reti neurali
 tre tensioni e tre rigidezze con due tagli
 energia di frattura e resistenza a trazione e compressione
 analisi di sensibilità
VANTAGGI
 molte più informazioni sul cls
 economicità
 tutto in situ
PROSPETTIVE
 martinetti con membrane
 controllo del volume d’olio
 “Digital Image Correlation” (DIC)
 ottimizzazione di geometria e modellazione
 applicazione a casi reali (?)
Effects of Alkali-Silica Reaction
Laboratory tests on concrete by Swamy and Al-Asali (1986)
tensile strength
elastic modulus
N/mm2
kN/mm2
40
30
20
0
3
6
9
Time, months
12
10
0
3
6
Time, months
+ expansion and, hence, self-stresses
9
12
Inverse analysis
forward operator
experiment
measured quantities
y
H (x)
model
parameters
computed quantities
exp
y comp
discrepancy function  minimized
*
x = arg min
x
( w (x) =
y
exp
-y
comp
(x)
2
)
Identification of elastic moduli and stresses
Step 1) measurement bases positioned
2) vertical and horizontal slots; displacements monitored;
3) flat-jack inserted and pressurized;
displacements monitored:
1)
2)
3)
25 cm
p
p
Identification of strength and fracture parameters
4) other slots generated
5) flat-jack pressurized in the “notch” to induce fracture
6) two flat-jacks to induce compressive failure
4)
5)
p
(  wedge-splitting test)
6)
( or separately)
Discrete cohesive crack model in mode I
t
 tt0
k
k
o

t2
0
2Gf
w
Gf
3 x 5 = 15
experimental data:
y
exp
least-square identification :
T
{s , k }
t*
0
*
æ
çç w = y exp - y comp (s 0t , k )
= arg min
s 0t , k ç
è
2
ö÷
÷÷
ø
Bayes batch identification
covariance matrix of experimental data :
C
exp
 s2l1




0
s
2
 l2
0

0


 y comp
L
 xT

ˆ L LC
ˆ L C
K C
0
0
T
ˆ
ˆ0,C
x
0
“sensitivity” matrix:
gain matrix :
T
a priori information :
exp

xˆ 0
1
residuals
xˆ  xˆ 0  K ( y
*
exp
y
*
ˆ
ˆ  K LC
ˆ
C C
0
0
comp
(xˆ 0 ) )
Kalman
filter is
sequential
Neural Network
trained by “patterns” generated by direct analyses
• input layer
• experimental data
yKI
hidden layers (architecture to optimize)
• output layer
• estimates
xO
Neurons with “weights” and “biases”
identified by genetic and backpropagation algorithms
Monte Carlo simulations combined with neural networks
H
experimental data randomly perturbed m times, m=1000
Bonferroni’s
y
exp j
95 % domain
ANN
ˆx j
sample of
m individuals
j  1... m  1000
95 % uncertainty
V
neural networks
ìï y exp üï
ï ï
í ý
ïï Ê ïï
îï þï
{s
t
0
Gf
T
}

t
0
training
testing
training
testing
estimates
estimates
Gf
ANN
16-4-2
back-propagation training identifies:
68 weights +6 biases
exact values [MPa]
not identifiable !
exact values [N/mm]
New dilatometric tests
A
stage 
hole A
D
stage 
B
A
• a hole B dug parallel to A
• diameter variations measured in A
0o
D
identification of stresses
stage 
• pressurization of A and B
• diameter variations measured
in A and B
B
A
p
p
identification of elastic moduli, tensile strength. fracture energy
II – DIAGNOSI GLOBALE CON CARICO IDROSTATICO STAGIONALE:
IDENTIFICAZIONE DI RIGIDEZZE COME INDICI DI DANNO
NOVITÀ
 condizioni al contorno identificate con termometri interni
 effetti termici periodici con sviluppi in serie
 radar confrontato con misure tradizionali
 approcci stocastici
 analisi di sensibilità
VANTAGGI
 risparmi anche computazionali
 ruolo del radar quantificato
 sensibilità orienta il progetto delle prove
PROSPETTIVE
 nonlinearità dei giunti
 diagnosi stocastica sequenziale con filtri di Kalman
 applicazione ad un caso reale
Overall modelling
Young moduli in ten homogeneous zones are assumed
as damage parameters
Loading conditions:
self weight
hydrostatic pressure upstream
hydrostatic pressure on the
reservoir bottom
thermal load
constrained
boundary
Monitoring by radar DInSAR
(Differential Interferometry
Synthetic Aperture Radar)
DISPLACEMENTS
Interferogram
RADAR
280 cm
monitoring 786 nodes on the downstream surface
Alternative loadings for static diagnostic analyses
“FAST” TEST

Reservoir level is changed
in a few days
“SEASONAL” TEST
°C
Service changes of
reservoir level
are exploited
Thermal effects must be considered
Thermal boundary conditions
Malla & Wieland (‘99)
Tup = d Tair – e
Tdown =  Tair + 
T [°C]
H
Tf = cost. = h
Bofang & Zhanmei (‘91)
Tw = c + (Ttop - c)e -fy
Tbot - e-fH Ttop
c=
1 - e-fH
y [m]
6 unknown parameters ,,d,e,f,h
Identification of thermal boundary conditions
Six unknown parameters
Experimental data:
internal temperatures by thermometers
thermometers
( 30 )
deterministic least-square
inverse analysis
Results of Fourier thermal analyses: annual periodicity
Temperature in nodes
steady-harmonic
Temperature [ °C ]
transient
Time [ Days ]
Monte Carlo results: radar vs traditional monitoring
Errors of mean values (250 samples)
Some sensitivity maps
2.5E-11
0.
duˆ m
dE j
Computed by direct differentiation
-2.5E-11 -5.E-11 -7.5E-11 -1.E-10 -1.25E-10 -1.5E-10 -1.75E-10 -2.E-10 -2.25E-10 -2.5E-10
 mm 
 MPa 
dam center high
2.5e-5
2.5E-11
0.
-2.5E-11
2.5E-11
2.5E -11
-2.5e-5
-5.e-5
-7.5e-5
-1.E-4
-1.25e-4
-1.5e-4
-1.75e-4
-2.e-4
-2.25e-4
-2.5E -11 -5.E -11 -7.5E -11 -1.E -10 -1.25E
-10 -1.5E
-10 -1.75E
-10 -2.E
-10 -2.25E
-10 -2.5e-4
-2.5E -10
duˆ m
dx2
dam center low upstream
Sensitivity of displacement in radar direction
Young modulus of zone "Dam Center High"
Z
Y
0.
0.
0.
-2.5E-11 -5.E-11 -7.5E-11 -1.E-10 -1.2
-5.E-11 -7.5E-11 -1.E-10 -1.25E-10 -1.5E-10 -1.75E-10 -2.E-10 -2.25E-10 -2.5E-10
X
2.5E-11
0.
-2.5E-11 -5.E-11 -7.5E-11 -1.E-10 -1.25E-10 -1.5E-10 -1.75E-10 -2.E-10 -2.25E-10 -2.5E-10
Sensitivity of displacement in radar direction
Young modulus of zone "Dam Center Low Upstream"
Z
Y
X
pulvino right
dam left low
III – CARATTERIZZAZIONE MECCANICA DI GEOMEMBRANE
CON “MEMBRANOMETRO”
NOVITÀ
 profilometro laser abbinato a scoppiometro
 simulazione e analisi inversa
 rete neurale
 quantificate proprietà elastiche, plastiche e viscose
(anche anisotrope!)
 approcci stocastici
 analisi di sensibilità
VANTAGGI
 molte informazioni
 prova biassiale (variabile con forma del foro)
 economicità
PROSPETTIVE
 controllo del volume d’olio
 “Digital Image Correlation” (DIC)
 realizzazione di prototipo ad hoc (?)
Present characterizasion technique
Reference norm: prEN 14151
Hypoteses:
Mariotte’s spherical geometry
Uniform strain along meridians
Undeformed thickness
pressurized vessel
strain vs. stress
pressure vs. max. displacement
60006
nominal stress [ MPa ]
1.8
1.6
pressure [ bar ]
tested membrane
50005
1.4
40004
1.2
1
3
3000
0.8
0.6
2
2000
0.4
1
1000
0.2
0
0
0
0
50
100
150
200
max. displecement [ mm ]
250
0
0
0.5
50
1.0
100
nominal strain
1.5
150
2.0
200
Experimental setup
Elastic-plastic-viscous model
Direct analyses
( Ramberg-Osgood )
σ
E
ee
ep
 
ε  1   S  1  2  pI  3   q 
E
2  k0 
S
3
SijSij   0 e p 
2
q
cr
e e&
n 1

2 cr cr
ε&ij ε&ij  A q m t -r
3
Identification: elastic-plastic range
viscous range
(Trust region alghoritm)
1.2
E/E0
/0
1.1
1
α/α0
n/n0
0.9
0.8
adim. parameters
adim. parameters
1.4
1.2
1
0.8
A/A0
m/m0
r/r0
0.6
0.4
0
10
20
30
iterations
40
50
0
10
20
iterations
30
40
IV - MODELLAZIONE DEL DANNO PRODOTTO DA AAR
NOVITÀ
VANTAGGI
 modello costitutivo multifase a danneggiamento per il cls
 effetti dell’evoluzione del campo termico nel corpo della diga
 effetti quali la dipendenza dell’evoluzione del fenomeno
dallo stato di sforzo preesistente sono automaticamente tenuti
in conto
 user material routine per il codice Abaqus
 approccio meccanicamente coerente
 relativamente pochi parametri addizionali da definire
rispetto ad un modello di cls monofase
 possibilità di uso in un codice commerciale ad ampia
diffusione
PROSPETTIVE
 comportamento anisotropo del cls
 viscosità del calcestruzzo
 tecniche di regolarizzazione più efficienti per
limitare l’influenza della mesh
Alkali-silica reaction (ASR-AAR)
The two phases of ASR development:
Silica of aggregates
(SiO2)
Alkali-silica gel
+ Alkali in concrete
Na+, K+
+ Water
1 aggregate over
10-20 reacts
Alkali-silica gel
Alkali-silica gel swelling
Non-homogeneous,
localised ASR development
1mm
100 m
Damage of mechanical material
properties
cement
mortar
aggregate
The AAR process consists basically of three periods:
• Initiation (less than 10 years): silica gel is produced by the reactive mineral phases
(disordered structures of poorly crystallized silica)
• Development (10 ÷ 30 years): silica gel exerts an increasing internal pressure as
result of a not univocally defined cause, i.e. absorption or imbibition of water or
osmotic pressure
• Rest: starts with the depletion of one of the three basic reactive components
(namely reactive silica, alkalis and water)
Pian Telessio dam, Central Plumbline (concio 4/6)
70
Measuring station 1
Measuring station 2
Measuring station 3
Measuring station 4
Crest Displacement
Crest Displacement Mean 12
Monte (mm)
60
50
40
20
10
1999
1990
1980
-10
1970
0
14/01/1970
08/07/1970
13/01/1971
13/07/1971
19/01/1972
06/07/1972
11/01/1973
03/07/1973
08/01/1974
03/07/1974
14/01/1975
01/07/1975
14/01/1976
15/07/1976
23/02/1977
29/08/1977
07/02/1978
25/08/1978
10/05/1979
26/11/1979
24/07/1980
08/01/1981
07/07/1981
12/01/1982
09/09/1982
12/05/1983
14/11/1983
15/05/1984
06/11/1984
07/05/1985
09/12/1985
13/06/1986
07/01/1987
07/07/1987
25/02/1988
12/10/1988
10/05/1989
06/11/1989
04/05/1990
09/01/1991
04/07/1991
09/01/1992
02/07/1992
09/02/1993
13/09/1993
04/03/1994
17/10/1994
29/05/1995
06/11/1995
02/05/1996
14/11/1996
02/07/1997
07/01/1998
05/08/1998
08/02/1999
Valle (mm)
30
Basic idea by Ulm – Coussy (2000)
Chemo-elastic plastic model
(Ulm, Peterson, Lemarchand, 2002)
concrete with expanding gel
bi-phase material
homogenized
concrete
skeleton
pressurised
gel
gel pressure
effective stress
macro stress
Biot’s coefficient
Basic idea by Ulm - Coussy
uniaxial model:
 macro   skeleton  bpgel
e
Eskeleton
Egel
gel

skeleton
pgel
 skeleton
ASR in a gravity dam
over-topping wave
14.8 m
37 m
ASR
air
91 m
103 m
reservoir
reservoir
pressure
selfweight
Geometry of Koyna dam
70 m
8000 4-nodes plane- strain elements (16300 dof)
over-topping
wave
14.8 m
air
19.2 m
winter
1  cos(t )
reservoir
summer
37 m
2
55 m
1.8
1.6
1.4
103 m
1.2
1
0.8
hydrostatic
loading
summer
0.6
winter
0.4
0.2
0
0
100
200
300
400
500
600
time [days]
4°
self-weight
10°
91.7 m
6°
70 m foundation
700
800
T
o
[ C]
20
15
10
5
0
0
100
200
300
400
time [ days ]

P
1
0.8
0.6
0.4
0.2
0
0
2
4
6
8
time [ year ]
10
12
14
16
over-topping height
135
hwave
hcrest
hwave [m]
130
1.26
125
1.20
120
115
110
12 year ASR
1.20
105
without ASR
100
95
-75
-60
-45
-30 -15 0
15
crest displacement
30
45
60
75
ucrest [mm]
60
0
30
crest displacement [mm]
1970
1980
time
reservoir
crest displacement
140
1990
2000
120
100
ucrest
80
[ mm ]
60
40
20
t
0
[ years ]
-20
valley
0
2
4
6
8
10
12
14
16
• Two-phase chemo-elastic-damage model for concrete
• Assuming full saturation the kinetic of ASR only
depends on temperature
• The proposed model allows for a good qualitative
description of ASR experimental tests
V – CALCOLO A ROTTURA GENERALIZZATO,
ANCHE CON DIFFUSIONE DI FESSURE SATURE
NOVITÀ
 massimizzazione del fattore di carico
vincolata non solo da equilibrio e plasticità
 programmazione matematica nonconvessa (MPEC)
 poroplasticità con saturazione totale
VANTAGGI
 coefficiente di sicurezza rispetto a:
collasso plastico a frattura o eccesso di deformazione
 ammesso attrito interno (non-associatività)
 è colto il ruolo delle infiltrazioni d’acqua
 risparmi computazionali
PROSPETTIVE
 implementazione in codice
 applicazione a un caso reale (?)
Applicazione a una diga a gravità
Diga di Ternay
(in muratura - Francia, 1864)
fessurazione diffusa
materiale bi-fase
(poroplasticità)
- materiale con scarsa duttilità
- spostamento al coronamento
inferiore al limite di esercizio
Programmazione Matematica
con “Vincoli di Equilibrio” (MPEC)
moltiplicatore
dei carichi
fattore
di sicurezza
congruenza + legame
costitutivo elastico
1


Cu

D
s Vl
problema di


T
ˆ
ˆ
programmazione
C s   t  t0


matematica


T
j  N s Hl Y  0

non lineare,
s  max  

 ,u , s , l , j
l 0
non convessa,




non regolare
B
l

L




j Tl 0
equilibrio
condizioni di
attivazione
fessurazione
variabili per
controllo
apertura
fessure
limitazioni su apertura
delle fessure
Valutazione della capacità portante,
con limitazione dello spostamento al coronamento
Stato piano di deformazione
Cond. di attivazione: Mohr-Coulomb
overtopping
PARAMETRI MECCANICI:
DIGA
peso proprio:
20 kN/m3
modulo di Young:
14 GPa
coeff. di Poisson:
0.15
coesione:
2 MPa
angolo attrito interno: f = 50°
angolo di dilatanza: 
FONDAZIONE
senza peso proprio
modulo di Young:
coeff. di Poisson:
coesione:
angolo attrito interno:
20 GPa
0.15
1.0 MPa
f = 30°
Mesh EF: 174 elementi, 395 nodi
variabili MPEC: 34199
vincoli MPEC:
34200
Valutazione della capacità portante,
con limitazione dello spostamento al coronamento
fattore di amplif.: 26
Valutazione della capacità portante,
con limitazione dello spostamento al coronamento
arresto prematuro
(dovuto al controllo di carico)
analsi incrementale (ABAQUS)
MPEC (=f=50°)
Stato piano di deformazione
Condizione di attivazione di Mohr-Coulomb
Valutazione della capacità portante,
con limitazione dello spostamento al coronamento
 = 30°
arresto prematuro
(dovuto al controllo di carico)
 = f = 50°
 = 10°
analsi incrementale (ABAQUS)
MPEC (=f=50°)
MPEC (<=f)
 = 0°
Stato piano di deformazione
Condizione di attivazione di Mohr-Coulomb
angolo
di attrito
interno
angolo di
dilatanza
Modello poroplastico con saturazione totale
Representative
volume
Solid skeleton
Fluid phase
variabili cinematiche
• Scheletro solido:
campo di spostamenti u
• Fase fluida:
flusso q (qi= volume che fluisce
secondo la direzione i attraverso
una superficie unitaria ortogonale
ad i nella unità di tempo)
variabili di deformazione
• Scheletro solido:
• Fase fluida:
deformazione media e=ee e p
contenuto fluido  =  e   p
(volume di fluido
per unità di volume rappresentativo)
variabili di sforzo
• Volume rappresentativo: sforzo “totale” 
• Fase fluida:
pressione del fluido p
Programmazione Matematica con “Vincoli di Equilibrio” (MPEC)
formulazione in ambito poroplastico
fattore
di sicurezza
moltiplicatore
dei carichi
congruenza + legame
costitutivo poro-elastico

Cu  D1 s D1R p ss  V l  equilibrio


T
ˆ
ˆ
C s   t  t0

 condizioni di

 attivazione
T
T
j  N s  N p p ss  H l Y  0 

s  max  
 fessurazione
 ,u , s , l , j
l 0



 variabili per
Bl L

 controllo
apertura
T


j l 0
 fessure
problema di programmazione matematica
non lineare, non convessa, non regolare
limitazioni su apertura
delle fessure
Valutazione della capacità portante,
con limitazione dello spostamento al coronamento
Modello semplificato (basato sulla diga di Ternay)
Stato piano di deformazione
5m
Cond. di attivazione: Drucker-Prager
40 m
overtopping
PARAMETRI MECCANICI:
DIGA
peso proprio:
modulo di Young:
coeff. di Poisson:
resistenza a compressione:
angolo “attrito interno”:
20 kN/m3
14 GPa
0.15
4 MPa
f = 25°
angolo di dilatanza:
=f
coeff. permeabilità: kx=10-11 m4/Ns
ky=10-12 m4/Ns
FONDAZIONE rigida
27 m
Mesh EF: 174 elementi, 395 nodi
variabili MPEC: 433
vincoli MPEC:
434
Overtopping (m)
[m]
overtopping
60
40
Exact integration
carico di collasso
LDA by MPEC
analisi incrementale
MPEC Collapse load
20
0
0
200
400
600
Crestdisplacement
displacement (mm)
crest
[mm]
Fine della sintesi dei risultati ottenuti dalla UdR-Polimi nei PRIN
su problemi strutturali delle dighe in calcestruzzo nel periodo 2004-2006