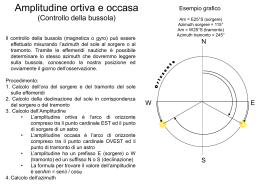
Analisi sulle Stagioni (Sole e sfera celeste)
Località: Civitavecchia (42°N)
•
Disegniamo la sfera celeste
•
Posizioniamo Zenit, Nadir e Orizzonte
•
A partire dallo zenit tracciamo la nostra
latitudine
•
Tracciamo l’equatore
•
Posizioniamo Pn (elevato) e Ps
(depresso)
•
Tracciamo i punti cardinali e i mezzicieli
•
Dato che la massima declinazione del
sole è 23°27’ (sia nord che sud)
tracciamo le due traiettorie del sole nei
due momenti (giorni) di massima
declinazione
Z
Ms
Pn
E
N
S
W
Ps
d = 23°27’N
Mi
d = 23°27’S
Z’
Analisi sulle Stagioni (Sole e sfera celeste)
Z
Ms
Pn
h
E
N
S
W
Ps
d = 23°27’N
Mi
Z’
Analizziamo il Giorno di massima declinazione
Nord (Solstizio d’Estate)
•
Il Sole Sorge in un punto tra Nord ed Est
(calcolabile con l’amplitudine, senAm =
send / cosj, Am = E 29,8 N, Az = 060,2)
•
Arriva al passaggio in meridiano (Il
calcolo dell’altezza del sole al passaggio
in meridiano è molto semplice, h = 90° - j
+ d = 90° - 42° + 23°27’ = 71°27’, la
declinazione si aggiunge perché
“omonima” della latitudine)
•
Il Sole tramonta in un punto tra Nord e
Ovest (calcolabile con l’amplitudine,
senAm = send / cosj, Am = W 29,8 N, Az
= 299,8)
•
Evidentemente la durata del giorno è la
maggiore dell’anno
Analisi sulle Stagioni (Sole e sfera celeste)
Z
Ms
Pn
h
E
N
S
W
Ps
Mi
d = 23°27’S
Z’
Analizziamo il Giorno di massima declinazione
Sud (Solstizio d’inverno)
•
Il Sole Sorge in un punto tra Sud ed Est
(calcolabile con l’amplitudine, senAm =
send / cosj, Am = E 29,8 S, Az = 119,8)
•
Arriva al passaggio in meridiano (Il
calcolo dell’altezza del sole al passaggio
in meridiano è molto semplice, h = 90° - j
- d = 90° - 42° - 23°27’ = 24°33’, la
declinazione si sottrae perché
“eteronima” della latitudine)
•
Il Sole tramonta in un punto tra Sud e
Ovest (calcolabile con l’amplitudine,
senAm = send / cosj, Am = W 29,8 S, Az
= 240,2)
•
Evidentemente la durata del giorno è la
minore dell’anno
Analisi sulle Stagioni (Sole e sfera celeste)
Analizziamo i due giorni di declinazione nulla
(d = 0°, il sole passa sull’equatore,
equinozi di primavera e di autunno)
•
Il Sole Sorge ad Est
•
Arriva al passaggio in meridiano (Il
calcolo dell’altezza del sole al passaggio
in meridiano è molto semplice, h = 90° - j
= 90° - 42° = 48°)
•
Il Sole tramonta ad Ovest
•
Evidentemente la durata del giorno è
uguale a quella della notte (non per caso
si chiamano “EQUInozi”)
Z
Ms
Pn
h
E
N
S
W
Ps
d = 0°
Mi
Z’
Analisi sulle Stagioni (Sole e sfera celeste)
Località: Wellington (Nuova Zelanda 42°S)
•
Disegniamo la sfera celeste
•
Posizioniamo Zenit, Nadir e Orizzonte
•
A partire dallo zenit tracciamo la nostra
latitudine
•
Tracciamo l’equatore
•
Posizioniamo Ps (elevato) e Pn
(depresso)
•
Tracciamo i punti cardinali e i mezzicieli
•
Dato che la massima declinazione del
sole è 23°27’ (sia nord che sud)
tracciamo le due traiettorie del sole nei
due momenti (giorni) di massima
declinazione
Z
Ms
Ps
W
S
N
E
Pn
d = 23°27’S
Mi
d = 23°27’N
Z’
Analisi sulle Stagioni (Sole e sfera celeste)
Z
Ms
Ps
h
W
S
N
E
Pn
d = 23°27’S
Mi
Z’
Analizziamo il Giorno di massima declinazione
Sud (Solstizio d’Estate)
•
Il Sole Sorge in un punto tra Sud ed Est
(calcolabile con l’amplitudine, senAm =
send / cosj, Am = E 29,8 S, Az = 119,8)
•
Arriva al passaggio in meridiano (Il
calcolo dell’altezza del sole al passaggio
in meridiano è molto semplice, h = 90° - j
+ d = 90° - 42° + 23°27’ = 71°27’, la
declinazione si aggiunge perché
“omonima” della latitudine)
•
Il Sole tramonta in un punto tra Sud e
Ovest (calcolabile con l’amplitudine,
senAm = send / cosj, Am = W 29,8 S, Az
= 240,2)
•
Evidentemente la durata del giorno è la
maggiore dell’anno
Analisi sulle Stagioni (Sole e sfera celeste)
Z
Ms
Ps
h
W
S
N
E
Pn
Mi
d = 23°27’N
Z’
Analizziamo il Giorno di massima declinazione
Nord (Solstizio d’inverno)
•
Il Sole Sorge in un punto tra Nord ed Est
(calcolabile con l’amplitudine, senAm =
send / cosj, Am = E 29,8 N, Az = 60,2)
•
Arriva al passaggio in meridiano (Il
calcolo dell’altezza del sole al passaggio
in meridiano è molto semplice, h = 90° - j
- d = 90° - 42° - 23°27’ = 24°33’, la
declinazione si sottrae perché
“eteronima” della latitudine)
•
Il Sole tramonta in un punto tra Nord e
Ovest (calcolabile con l’amplitudine,
senAm = send / cosj, Am = W 29,8 N, Az
= 299,8)
•
Evidentemente la durata del giorno è la
minore dell’anno
Analisi sulle Stagioni (Sole e sfera celeste)
Analizziamo i due giorni di declinazione nulla
(d = 0°, il sole passa sull’equatore,
equinozi di primavera e di autunno)
•
Il Sole Sorge ad Est
•
Arriva al passaggio in meridiano (Il
calcolo dell’altezza del sole al passaggio
in meridiano è molto semplice, h = 90° - j
= 90° - 42° = 48°)
•
Il Sole tramonta ad Ovest
•
Evidentemente la durata del giorno è
uguale a quella della notte (non per caso
si chiamano “EQUInozi”)
Z
Ms
Ps
h
W
S
N
E
Pn
d = 0°
Mi
Z’
Analisi sulle Stagioni (Sole e sfera celeste)
1° Caso particolare: osservatore tra i due tropici
Z
Ms
h
E
Pn
N
S
W
Mi
d = 23°27’N
d = 23°27’S
Z’
Ps
Località: Puerto Lempira (15°N - Honduras)
•
Disegniamo la sfera celeste
•
Posizioniamo Zenit, Nadir e Orizzonte
•
A partire dallo zenit tracciamo la nostra
latitudine
•
Tracciamo l’equatore
•
Posizioniamo Pn (elevato) e Ps
(depresso)
•
Tracciamo i punti cardinali e i mezzicieli
•
Dato che la massima declinazione del
sole è 23°27’ (sia nord che sud)
tracciamo le due traiettorie del sole nei
due momenti (giorni) di massima
declinazione
•
Considerando le stesse procedure delle
lastrine precedenti e tralasciando il
calcolo dell’azimuth al sorgere ed al
tramonto, dal disegno emergono alcune
considerazioni importanti:
• Per due giorni all’anno il sole passa
sullo zenith (h = 90°)
• Per alcuni giorni vicini al giorno del
solstizio d’estate (prima e dopo) il
calcolo dell’altezza si fa allo stesso
modo ma viene maggiore di 90° (es:
90° - 15° + 23°27’ = 98° 27’).
Ovviamente bisogna calcolare
l’angolo supplementare (h = 180° 98° 27’ = 81°33’). Vedere il disegno.
• Si nota che l’altezza del sole, la
durata del giorno e l’angolo di
incidenza dei raggi solari variano di
poco. In questo caso le stagioni
sono 2, stagione umida e stagione
secca.
Analisi sulle Stagioni (Sole e sfera celeste)
2° Caso particolare: osservatore in zona circolo polare
Z
Pn
E
Ms
N
Mi
S
W
d = 23°27’N
d = 23°27’S
Z’ Ps
Località: Isola Jan Mayen (71°N – Mare Artico)
•
Disegniamo la sfera celeste
•
Posizioniamo Zenit, Nadir e Orizzonte
•
A partire dallo zenit tracciamo la nostra
latitudine
•
Tracciamo l’equatore
•
Posizioniamo Pn (elevato) e Ps (depresso)
•
Tracciamo i punti cardinali e i mezzicieli
•
Dato che la massima declinazione del sole è
23°27’ (sia nord che sud) tracciamo le due
traiettorie del sole nei due momenti (giorni) di
massima declinazione
•
Considerando le stesse procedure delle
lastrine precedenti e tralasciando il calcolo
dell’azimuth al sorgere ed al tramonto, dal
disegno emergono alcune considerazioni
importanti:
• Per alcuni giorni vicini al giorno del
solstizio d’inverno (prima e dopo) il sole
è sempre sotto l’orizzonte (non si può
dire, ma l’altezza viene negativa).
• Per alcuni giorni vicini al giorno del
solstizio d’estate (prima e dopo) il sole
non tramonta mai (è sempre sopra
l’orizzonte. Ovviamente se ci si trova
proprio sul polo (impossibile con una
nave per ovvi motivi) ci sono due periodi
di sei mesi (“notte polare” e “giorno
polare”)
• Si nota che l’altezza del sole è sempre
molto bassa, così come l’angolo di
incidenza dei raggi solari è quasi
tangente. Anche qui non esistono le
quattro stagioni.