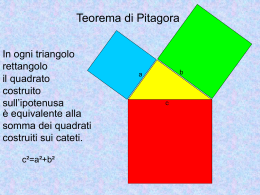
IL TEOREMA DI PITAGORA
La prima dimostrazione di questo teorema è stata
attribuita al matematico greco Pitagora di Samo (570-500
a. C.). Non si sa, però, come Pitagora abbia condotto la
sua dimostrazione perchè nulla è rimasto delle sue opere.
La prima dimostrazione che conosciamo fu data da
Euclide (300 a. C.) nei suoi Elementi . Da quel momento
molti matematici e non matematici, sono stati così attratti
da questo teorema che hanno sentito il bisogno di
elaborare un ingegnoso e alternativo modo per
dimostrarlo. Elisha Scott Loomis nel suo libro The
Pythagorean Proposition pubblicato nel 1940, riporta ben
370 diverse dimostrazioni di questo teorema. Nessun altro teorema ha ricevuto tanta
attenzione e tante dimostrazioni, nonostante ciò ogni anno vengono pubblicate, dalle
riviste matematiche, nuove dimostrazioni.
Perché c'è stato tanto interesse su questo teorema? Ha un enunciato semplice e una
facile dimostrazione e può essere pienamente compreso da un ragazzo di tredici anni.
Ha numerose applicazioni e spesso è indispensabile per risolvere molti tipi di
problemi. Eppure questo teorema così comprensibile ha cambiato radicalmente il
corso della matematica. Grazie a questo teorema la matematica, che era nata per
soddisfare esigenze concrete legate alla realtà pratica, si è trasformata in una scienza
che abitua a ragionare. Nella geometria euclidea, questo teorema, è fondamentale. Ha
permesso di scoprire l'esistenza di segmenti incommensurabili.
Questa conoscenza ha fatto capire che gli oggetti geometrici non possono essere
identificati come degli oggetti concreti e che il punto geometrico non può avere
dimensioni. E' un teorema geometrico, eppure ha permesso di scoprire i numeri
irrazionali. Da questa conoscenza si è capito che i numeri naturali sono adatti a
rappresentare solo grandezze discrete. Per rappresentare grandezze continue
occorrono oltre ai numeri razionali anche i numeri "irrazionali". Gli egiziani hanno
usato questo teorema per costruire un angolo retto, i greci l'hanno utilizzato per
costruire una vasta rete di idee matematiche. Nel corso dei secoli è stato utilizzato per
costruire alcune branche della matematica moderna. E' stato il suggeritore di proficue
ricerche nel campo della teoria dei numeri.
Verifichiamo il
Teorema di Pitagora
EnunciatoEnunciato:
In un triangolo rettangolo il
quadrato costruito
sull’ipotenusa è equivalente
alla somma dei quadrati
costruiti sui cateti
IL TRIANGOLO RETTANGOLO
IPOTENUSA
CATETO
MINORE
i
C2
C1
CATETO
MAGGIORE
Quadrato costruito
sull’ipotenusa
Quadrato costruito
sul cateto minore
Quadrato costruito
sul cateto maggiore
i
Costruiamo 3 quadrati :
c1
c2
G
R
V
l=i
l = c2
l = c1
Sistemiamo al loro posto i quadrati
G
V
V
R
R
e infine
Prima
Poi ililVERDE
ilGIALLO
ROSSO
V
Q
R
Scomponiamo i quadrati per mezzo del quadratino Q
G
V
Q
R
Riportiamo i quadratini uno per uno su quello GIALLO
G
Q
V
R
prima i ROSSI
G
V
Q
R
G
Q
R
V
Q
G
Q
R
V
Q
poi i VERDI
G
R
V
Q
G
V
R
il quadrato GIALLO è stato riempito totalmente
dal ROSSO e dal VERDE
Q
Pertanto:
GIALLO
VERDE
GIALLO = ROSSO + VERDE
ROSSO
Ma
GIALLO
VERDE
GIALLO = i
2
2
ROSSO = c 1
ROSSO
2
VERDE = c2
Allora
GIALLO
2
2
1
i =c +c
VERDE
Da cui:
ROSSO
2
2
Allora
GIALLO
VERDE
i=
c12 + c22
2
2
c1= i - c2
ROSSO
c2=
2
2
i c1
Teorema di Pitagora applicato ad un
problema
Problema
In un triangolo rettangolo i cateti
misurano rispettivamente cm 4 e cm 3.
Trova il perimetro.
Dati:
i
c1
c1= cm 4
c2= cm 3
Richiesta: P = c1+c2+i
c2
incognita
Soluzione
i=
c21 + c2 2 = cm 42 +32
= cm 25
= cm 16 +9
=cm 5
P = c1+c2+i= cm(3+4+5)= cm12
Applicazione
del
teorema
alle figure
piane
Applicazione
del
teorema
alle figure
piane
Altra applicazione del T. di Pitagora
Problema
In un triangolo isoscele la base e
l’altezza misurano rispettivamente cm 10
e cm 12.
Trova il perimetro.
b= cm 10
h= cm 12
Dati:
cateto
l
l
h
b
ipotenusa
Richiesta:
b/2
P = 2l+b
incognita
cateto
Soluzione
l=
(b/2)2 + h2
= cm
25 +144
= cm
= cm
52 +122
169
=cm 13
P = 2l+b= cm(13x2+10)= cm36