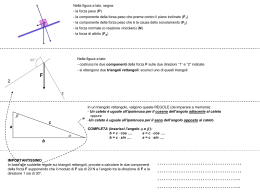
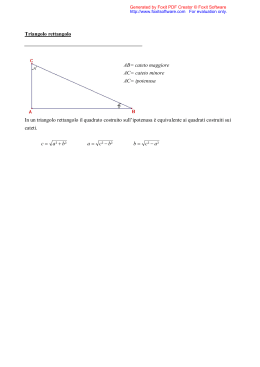
2
C
2
c
2
i
+ =
2
2
2
8 +6 =i
64 + 36 = 100
i  C c
2
2
Q1
Q1+ Q2
c2
i2
C2
Q2
Q1 + Q2
Q1
Q2
I pezzi della figura accanto
corrispondono alla somma di
quella verde e quella gialla.
Q1 + Q2
Formula diretta
c
a
t
e
t
o
i 
C c
2
2
Formule inverse
cateto
C
i c
2
c
i C
2
2
2
a
l
t
e
z
z
a
base
d h b
2
c
a
t
e
t
o
2
h  d b
2
b  d h
2
2
cateto
2
l
a
t
o
lato
d  l l
2
2
 l x2  l 2
l  d :2  d : 2
2
2
2
l  (b / 2)  h
h
b/2
C
a
t
e
t
o
=
h Cateto =b/2
h  l - (b / 2)
2
b/2  l - h
2
2
2
2
Teorema di Pitagora applicato al triangolo isoscele.
Dati
C
h=12cm
b=10cm
lato=?
P=?
CH=altezza=cateto
h=12cm
HB=1\2base=cateto
A
B
H
CB=lato=ipotenusa
b=10cm
CB  HB  CH  5  12  25  144  169  13
2
2
2
2
13*2=26 cm 2 lati
perimetro= base + 2 lati = 10 +26= 36 cm
l  ( D / 2)  (d / 2)
2
D/2
D / 2  l - (d / 2)
2
d/2
d / 2  l - (D/2)
2
c
a
t
e
t
o
cateto
2
2
2