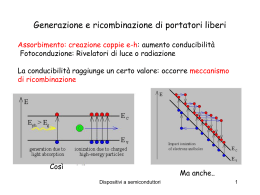
A.A. 2013 – 2014 ESPERIMENTAZIONI DI FISICA 3 Programma del corso • • • • • Dispositivi a semiconduttore. Transistor. Amplificatori. Elettronica digitale. Rumore elettrico. Testi di riferimento: -Millman Grabel Microelectronics Mc Graw-Hill (fuori stampa) - Appunti in rete. Esp- 3 - Semiconduttori AA13-14 1 Dispositivi a semiconduttori Semiconduttori Conduzione nei metalli Conduzione nei semiconduttori Drogaggio dei semiconduttori Giunzione pn Esp- 3 - Semiconduttori AA13-14 2 STRUTTURE DEI SOLIDI • Classificazione generale dei solidi AMORFO CRISTALLINO Esp- 3 - Semiconduttori AA13-14 POLICRISTALLINO 3 SOLIDI CRISTALLINI • I solidi di cui ci occupiamo hanno una struttura cristallina: gli atomi sono disposti in modo regolare (reticolo) • Gli atomi sono legati medianti gli elettroni più esterni (elettroni di valenza) Esp- 3 - Semiconduttori AA13-14 4 STRUTTURA ATOMICA • Elettroni di valenza 3s2 2s2 1s2 Z=14 A=28.1 • Gruppi di più elettroni circondano il nucleo negli «orbitali» (modello atomico di Bohr). • Gli elettroni più esterni 2p6 determinano le proprietà chimiche e di conduzione dell’atomo 3p2 Esp- 3 - Semiconduttori AA13-14 5 FORMAZIONE DELLE BANDE Forma del potenziale (app.) NUCLEO LIVELLI ENERGETICI POSSIBILI Esp- 3 - Semiconduttori AA13-14 6 FORMAZIONE DELLE BANDE Energia BANDA DI CONDUZIONE 3p2 GAP 3s2 BANDA DI VALENZA Passo reticolare Esp- 3 - Semiconduttori AA13-14 7 CLASSIFICAZIONE DEI SOLIDI Energia Banda di conduzione Banda proibita “GAP’’ Eg Banda di valenza Isolante Metallo Semiconduttori alla temperatura ambiente Esp- 3 - Semiconduttori AA13-14 8 IL MODELLO DI DRUDE della CONDUZIONE ELETTRICA Assunzioni: Gli elettroni in un conduttore 1. Non interagiscono tra loro (gas perfetto) 2. L’interazione tra gli elettroni e gli atomi del reticolo è istantanea 3. Dopo l’urto direzione è casuale e la velocità (modulo) dipende dalla temperatura Esp- 3 - Semiconduttori AA13-14 9 LA CORRENTE ELETTRICA NEL MODELLO DI DRUDE Moto degli elettroni di conduzione E=0 uE uE u : velocità di deriva Mobilità ut Nq n(u t S )q t t qnuS I S E≠0 j I 1 qnu qn E E E ( A / m 2 ) S S 1 I qn ESl / l (qn ) V V l R Esp- 3 - Semiconduttori AA13-14 10 LA CONDUZIONE ELETTRICA nei METALLI • Nei metalli i portatori di carica “liberi” sono solo gli elettroni, per cui la densità di corrente si scrive: j qnud qnE E ( A / m 2 ) ud E m / s n: densità di portatori (elettroni) disponibili per la conduzione ~ 1021 cm-3 ud: velocità di deriva dei portatori (elettroni) σ: conduttività del materiale ~ 105 (Ω cm)-1 µ: mobilità dell’elettrone ~ 500 cm2(Vs)-1 Esp- 3 - Semiconduttori AA13-14 11 LA CONDUZIONE ELETTRICA nei METALLI e nei SEMICONDUTTORI METALLO (Cu) SEMICONDUTTORE Atomi per cm3 8.5 1022 CONCENTRAZIONE PORTATORI 5 10 21 MOBILITA’ 500 (cm2/V s) 1400 – 450 (cm2/V s) CONDUCIBILITA’ 105 (Ω cm)-1 2.5 10-6 (Ω cm)-1 (cm-3) (cm-3) Esp- 3 - Semiconduttori AA13-14 5 1022 (cm-3) 1.45 1010 (cm-3) 12 SEMICONDUTTORI (intrinseci) Esp- 3 - Semiconduttori AA13-14 13 SILICIO intrinseco Struttura cristallina con cella elementare cubica a facce centrate Proprietà Valore Numero atomico 14 Elettroni di valenza 4 Atomi per cm3 5 1022 Eg @ 300K (eV) 1.12 Conc. intr.@ 300K (cm-3) 1.45 1010 Conduttività @ 300K (Ωcm)-1 5 10-6 Esp- 3 - Semiconduttori AA13-14 +4 +4 +4 +4 +4 +4 +4 +4 +4 +4 +4 +4 14 Conduzione mediante le «LACUNE» Energia La mancanza di un elettrone è simulata da una carica positiva detta “lacuna” o “buca” Campo elettrico Livello energetico della Banda di conduzione L’elettrone si muove con la sua mobilità n Eg Atomo Eg Elettrone Altri elettroni possono occupare la buca libera + + + + + + + La “lacuna” si muove con la sua mobilità, p, in senso opposto agli elettroni Esp- 3 - Semiconduttori AA13-14 16 Portatori di carica nei semiconduttori •Nei semiconduttori sia gli elettroni sia le lacune contribuiscono, indipendentemente, alla conduzione. •I meccanismi cui sono soggetti elettroni e lacune nel reticolo sono differenti e di conseguenza le mobilità dei due tipi di portatori sono differenti. Esp- 3 - Semiconduttori AA13-14 17 La densità di corrente elettrica nei semiconduttori Carica dell’elettrone Campo elettrico j q (n n p p ) E Concentazione di elettroni Concentazione di lacune Mobilità delle lacune Mobilità degli elettroni Nei semiconduttori i portatori di carica sono sia gli elettroni sia le lacune Esp- 3 - Semiconduttori AA13-14 18 La corrente di diffusione Nei semiconduttori ci può essere un accumulo di portatori (elettroni o lacune): la densità dei portatori dipende dalla coordinata. Ad esempio per le lacune p=p(x) p(x) x Il numero dei portatori che attraversano una sezione ideale del semiconduttore, nel senso che va dalla concentrazione più alta a quella più bassa è maggiore di quelli che vanno in senso inverso. Questo fenomeno definisce la corrente di diffusione, la cui espressione è (per le lacune): (dettagli) dp j qD p dx D: coefficiente di diffusione . Si misura in (m2/s) Esp- 3 - Semiconduttori AA13-14 19 Corrente di diffusione T ≠0 p(x) u: velocità media dei portatori t : tempo di collisione l l: cammino libero medio u t p ,left right Materiale aggiuntivo p ,rightleft -l 0 l x 1 u p (l ) p p ,left right p ,right left 1 u [ p(l ) p(l )] 2 2 1 u p (l ) lu p(l ) p(l ) lu dp( x) 2 2l dx dp ( x) dp qD p dx dx dn( x) dn jn ( x) qlu qDn dx dx j p ( x) qlu corrente di diffusione lacune corrente di diffusione elettroni Esp- 3 - Semiconduttori AA13-14 20 La corrente di diffusione (cont.) Per gli elettroni l’espressione della corrente di diffusione ha il segno opposto perché gli elettroni hanno carica negativa: dn j qDn dx In generale le correnti di lacune ed elettroni in un semiconduttore saranno la somma della corrente di deriva e di quella di diffusione: dp j p q p p E D p dx dn jn q n n E Dn dx Esp- 3 - Semiconduttori AA13-14 21 Semiconduttori intrinseci • I semiconduttori puri (intrinseci) sono pessimi conduttori a temperatura ambiente. • Esempio. Resistenza a 300 K di: • (Tabella resistività) Si 100 µm 1 mm 2 mm 1 2 2 S 10 10 cm 3 R 2.3 105 cm 1 2 . 3 10 1 l 2 10 cm • Resistenza per il rame 1 2 2 10 10 cm 9 R 1.69 106 cm 1 8 . 5 10 1 2 10 cm Esp- 3 - Semiconduttori AA13-14 22 Semiconduttori estrinseci o drogati • Inserendo delle impurità nel semiconduttore (atomi diversi da quelli che lo formano) la sua conducibilità elettrica può cambiare sensibilmente. • Un semiconduttore nel quale sono inserite delle impurità viene detto estrinseco o drogato. • La frazione di atomi sostituiti tipicamente è compresa nell’intervallo10-3 – 10-9 • Il drogaggio può essere fatto in due modi: – Con atomi pentavalenti (donori) – Con atomi trivalenti ( accettori) Esp- 3 - Semiconduttori AA13-14 23 Semiconduttori drogati di Tipo n • Drogati con atomi pentavalenti (Antimonio, Fosforo e Arsenico) diventano semiconduttori di tipo n Silicio elettrone libero Impurezza pentavalente +4 +4 +4 +4 +4 +4 +4 +4 +4 +5 +4 +4 Esp- 3 - Semiconduttori AA13-14 24 Semiconduttori drogati di Tipo p • Drogati con atomi trivalenti (Boro, Gallio e Indio) diventano semiconduttori di tipo p Silicio +4 +4 +4 +4 lacuna +4 +4 +4 +4 Impurezza trivalente +4 +3 +4 +4 Esp- 3 - Semiconduttori AA13-14 25 Semiconduttori drogati • Le impurezze aggiunte al semiconduttore sono tutte ionizzate (E=0.05eV) quindi contribuiscono alla conduzione • La concentrazione delle impurezze è dell’ordine di 1 atomo (donore o accettore) per 108 atomi di semiconduttore. • Quindi la concentrazione di portatori dovuti alle impurezze è: 5x1014 cm-3 • questo numero va confrontato con la concentrazione intrinseca 1.5x1010 cm-3: 104 volte più piccola! (La conduttività è 0.1 (Ω cm)-1) Esp- 3 - Semiconduttori AA13-14 26 Legge di azione di massa In un semiconduttore, intrinseco o drogato, avvengono i seguenti fenomeni: 1. sono create in continuazione coppie elettrone – lacuna con una velocità C che dipende dalla temperatura:=C(T) 2. ogni volta che un elettrone e una lacuna si incontrano avviene un fenomeno di annichilazione o ricombinazione ed entrambi i portatori scompaiono (in realtà l’elettrone non scompare ma assume una posizione fissa nel cristallo e non è più disponibile per la conduzione). Indichiamo con R il numero di queste ricombinazioni nell’unità di tempo; R dipenderà sia dalla temperatura sia dal prodotto delle concentrazioni di elettroni (n) e lacune (p) : R= n p f(T) 3. All’equilibrio la creazione di coppie e la loro ricombinazione dovranno essere uguali: R= C, per cui il prodotto np dipende solo dalla temperatura e non dal drogaggio. Potremo quindi uguagliare np a ni2 dove ni è la concentrazione del semiconduttore intrinseco. 4. La legge di azione di massa di esprime quindi come: np ni2 Esp- 3 - Semiconduttori AA13-14 27 La giunzione pn tipo p - - - tipo n - - + + + + + + + + + + + + + + + + + + + + diffusione delle buche nella zona tipo-n e ricombinazione diffusione degli elettroni nella zona tipo-p e ricombinazione lacune Impurezze trivalenti elettroni Zona di svuotamento (depletion region) Esp- 3 - Semiconduttori AA13-14 Impurezze pentavalenti 28 tipo p La giunzione pn Si ottiene giustapponendo due semiconduttori uno di tipo p e l’altro di tipo n tipo n d 2V dx 2 x E ( x) wp ( x' ) dx' Barriera di potenziale Esp- 3 - Semiconduttori AA13-14 29 La giunzione pn concentrazione lacune ed elettroni - tipo p log( n, p) - - - - + + + + + + + + + + + + + + + + + + + + NA ND n ni2 /NA tipo n p ni2 /ND Portatori Maggioritari minoritari x applet giunzione pn • http://oes.mans.edu.eg/courses/SemiCond /applets/education/pn/pnformation/pnfor mation.html Esp- 3 - Semiconduttori AA13-14 31
Scaricare