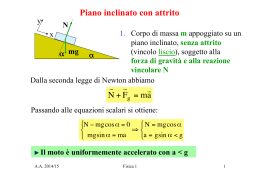
Polo per la Chimica e le Biotecnologie Ambientali e
Sanitarie
Istituto d’Istruzione Superiore
Ada Gobetti Marchesini – Luigi Casale
– Torino
Orientamento Formativo in collaborazione con
il Politecnico di Torino
Prof. Pietro MANTELLI
[email protected]
LEZIONE 4
Tratta da materiale didattico predisposto dal Politecnico di
Torino
Orario delle lezioni:
dal 11/11/2014 al 16/12/14
martedi -14:30 – 15:50 aula 2 lim
http://orienta.polito.it/OrientamentoFormativo.html
ENERGY- ENERGIA
“quel
bambino
ha tanta
energia”
“il giocatore è
rimasto senza
energia alla fine
della partita”
Energia - deriva dal greco “en-ergon”, letteralmente
“capacità di svolgere lavoro”
L’energia è un numero!
L’energia nel SI si misura in
joule
J
Energia
a) meccanica
d) elettrica
b) termica
e) chimica
c) eolica
f) nucleare
Che cos’è l’ENERGIA?
“E’ una cosa astratta, puramente
matematica, un numero che non
cambia col tempo. Non riesco a
spiegarvelo meglio di così!”
Richard Feynman, premio Nobel per la fisica, 1965.
Una madre lascia giocare il figlioletto con dei dadi. Nonostante alcuni
movimenti (dadi sotto il tappeto, in una scatola chiusa, nellacqua della vasca
da bagno, fuori dalla finestra) alla fine la madre osserva che il numero dei
dadi è sempre lo stesso.
1963: Richard Feynman “Dennis (Pierino) e i dadi”
(vedi anche: La legge fisica, Boringhieri, cap.3)
Uno studente di medicina fa l’esame di laurea.
I professori in toga gli chiedono: “perché l’oppio fa dormire?”
Lo studente è incerto, tentenna.
Improvvisamente ha una ispirazione: l’oppio fa dormire
perché ha la “virtus dormitiva” (capacità di far dormire)!
I professori sono molto soddisfatti, lo studente è promosso.
Gli spettatori ridono perché pensano sia una pseudospegazione.
Molière 1673: “Il malato immaginario”
WORK - LAVORO
Il lavoro è l’energia trasferita a un corpo per
mezzo di una forza.
E2
E1
v2
Energia ceduta al corpo
-
lavoro > 0
Energia ceduta dal corpo
-
lavoro < 0
LAVORO DI UNA FORZA
Applicando una forza non equilibrata ad una massa se ne determina uno
spostamento e una variazione di velocità.
Si definisce LAVORO il prodotto scalare fra la FORZA applicata e lo
SPOSTAMENTO compiuto

B
A
Eseguendo il prodotto scalare si ottiene
7
LAVORO DI UNA FORZA
casi
1)
2)
3)
4)
Se -90°< θ < 90° il LAVORO è positivo (L > 0)
Se 90°< θ < 270° il LAVORO è negativo (L < 0)
Se θ = 90°; θ = -90° il LAVORO è nullo (L = 0)
Se θ = 0 il LAVORO assume il valore massimo
L AB   FABcos    FAb AB

B
A
8

B
A
L AB  0
B
A
9
LAVORO FATTO DALLA FORZA PESO
P
h
s
LAVORO FATTO DALLA FORZA PESO SUL PIANO INCLINATO
y
A
x
m 
Pt  mgsin
h
Pn  mgcos


C
B
P
Il lavoro non dipende dall’inclinazione, ma solo dal “dislivello” fra i punti A e B.
Il lavoro è indipendente dal percorso! Il lavoro fatto su un percorso chiuso è
sempre uguale a zero: LA FORZA DI GRAVITA’ E’ CONSERVATIVA
LAVORO DELLA FORZA DI ATTRITO
Fd
s
La forza di attrito svolge un LAVORO sempre NEGATIVO perché forza e
spostamento hanno sempre verso opposto.
LAVORO FATTO DALLA FORZA DI ATTRITO SUL PIANO INCLINATO
y
Il lavoro dipende
dal percorso!
Il lavoro fatto su
un percorso chiuso
è diverso da zero:
LA FORZA DI
ATTRITO NON E’
CONSERVATIVA
m 
x
Fd = m d N = m d mgcosJ


A
h
Pn  mgcos
C
B
P
LAVORO FATTO DA UNA FORZA COSTANTE
F
B
A
C
D
0
s
1
s
s
2
LAVORO FATTO DA UNA FORZA VARIABILE
Esempio: il moto avviene su una retta (asse x), la forza è parallela
all’asse x e il suo modulo dipende dalla posizione.
F(x)
Li = Fi Dxi
F0
Fi = costante
F1
Fi L
i
A
xi
In un diagramma F(x), il lavoro
è rappresentato dall’area della
superficie sotta la curva.
L = lim
B
xi
x
L=
B
0
i
Fi x i
ò F(x)dx = area
A
ESERCIZIO
Determinare il lavoro svolto da una persona per trascinare in salita
(senza attrito e con attrito, μd = 0.3) un corpo di massa m = 10kg su
un piano inclinato di angolo α = 30°, con una velocità costante, da un
punto A situato alla base del piano inclinato fino ad un punto B situato ad
una altezza h = 5m.
LAVORO FATTO DALLA FORZA ELASTICA
F = -kDx
L0
Fel
A
x
B
A
Fe
-k∆x
LA FORZA ELASTICA’ E’ CONSERVATIVA
Fel
1
1
LBA = (-kDx)(Dx) = kDx 2
2
2
∆x
∆x
L0
1
1
LAB = (-kDx)(Dx) = - kDx 2
2
2
∆x
∆x
Lavoro = area sotto la linea
che descrive Fel (x)
x
A
-k∆x
Fe
1
1
LABA = kDx 2 - kDx 2 = 0
2
2
Forze non conservative:
forza di attrito, forza di resistenza dell’aria, forza magnetica
Forze conservative:
forza elastica, forza di gravità, forza elettrostatica
SE IL CAMPO E’ CONSERVATIVO IL LAVORO DIPENDE SOLO DALLA
POSIZIONE INIZIALE E FINALE
POTENTIAL ENERGY
UN CORPO SOGGETTO A FORZE CONSERVATIVE POSSIEDE UNA
ENERGIA CHE DIPENDE SOLO DALLA SUA POSIZIONE:
QUESTA ENERGIA SI CHIAMA POTENZIALE
CORRISPONDE AL LAVORO CHE LE FORZE DEL CAMPO FANNO
PER FARGLI CAMBIARE POSIZIONE
ENERGIA POTENZIALE GRAVITAZIONALE
EP = mgh
h1
h2
ENERGIA POTENZIALE ELASTICA
1 2
EP = kx
2
L0
A
∆x
B
A
Fe
∆x
L0
A
KINETIC ENERGY

v1

v2
L’energia cinetica è l’energia associata alla VELOCITÀ di un corpo
1 2
K = mv
2
CONSERVAZIONE DELL’ENERGIA
Che cos’è l’ENERGIA?
“E’ una cosa astratta, puramente matematica,
un numero che non cambia col tempo.
Non riesco a spiegarvelo meglio di così!”
Richard Feynman, premio Nobel per la fisica, 1965.
ENERGIA MECCANICA
Energia potenziale
Energia cinetica
Energia meccanica
L’ENERGIA MECCANICA SI CONSERVA ?
SOLO IN PRESENZA DI FORZE CONSERVATIVE
NO IN PRESENZA DI ATTRITO
TEOREMA DELL’ENERGIA CINETICA
Energia cinetica
iniziale
Lavoro compiuto
Energia cinetica a
lavoro compiuto
1 2 1 2
L = K B - K A = mv B - mv A = DK
2
2
Se agiscono più forze su un corpo, il
lavoro totale è la somma dei lavori
EP = _______
EC = _______
ESERCIZI:
CONSERVAZIONE ENERGIA MECCANICA
(senza attriti)
E M = _______
v
=0
h
= _______
EP = _______
EP =
EC =
EC = _______
EM =
v=
EP = _______
EC = _______
E M = _______
v
= 8m / s
h
=0
E M = _______
h=
v
= _______
h
= 1m
EP = _______ EP = _______ EP = _______ EP = _______ EP = _______
EC = _______ EC = _______ EC = _______ EC = _______ EC = _______
EM = _______ EM = _______ EM = _______ EM = _______ E M = _______
v = 15m / s
v = _______ v = _______ v = _______ v = _______
h = 2m
h = 10m
h = 5m
h =0
h = 7m
EP = _______ EP = _______ EP = _______ EP = _______
EC = _______ EC = _______ EC = _______ EC = _______
E M = _______ E M = _______ E M = _______ E M = _______
v
= _______ v
= 8m / s
v
=
v
= 6m / s
h
= 4m
= 3m
h
=0
h
= _______
h
Racing balls- skiers
PROVARE!
Two balls roll down two different lowfriction tracks near the Earth's surface. The
user is invited to predict which ball will reach
the end of the track first. This problem is
difficult for many beginning Physics students.
http://www.upscale.utoronto.ca/Gen
eralInterest/Harrison/Flash/ClassMec
hanics/RacingBalls/RacingBalls.html
The "Racing Balls" animation which is
accessed via the above line sometimes
triggers cognitive dissonance and
rejection in beginning students. For
some of these, changing the balls to
skiers helps to clarify the situation, and
that is what this animation does. The
"Racing Balls" one should be used with
students first.
http://www.upscale.utoronto.ca/Gen
eralInterest/Harrison/Flash/ClassM
echanics/RacingSkiers/RacingSkier
s.html
Esercizi:
1. Determinare la velocità con la quale un corpo, che parte da
fermo dal punto più alto di un piano inclinato di angolo α = 30° e
di altezza h = 3 m, arriva alla base del piano inclinato: a) in
assenza di attrito e b) con attrito, μd = 0.3.
2. Determinare la velocità di un corpo di massa m = 0.5 kg
attaccato ad una molla di costante k = 200 N/m quando passa
per la posizione di equilibrio (molla in posizione di riposo) se si
conosce che al momento iniziale l’allungamento della molla è
∆x = 5 cm.
Esercizio:
Un cavallo trascina a velocità costante una slitta di massa m = 100 kg
lungo una salita coperta di neve, inclinata di un angolo α = 30°
rispetto all’orizzontale,
superficie.
esercitando
una
forza
parallela
alla
Il coefficiente di attrito dinamico tra la slitta e la neve è 0.15.
Sapendo che la potenza sviluppata dal cavallo è W = 300 watt, calcolare la
velocità con cui sale la slitta.
