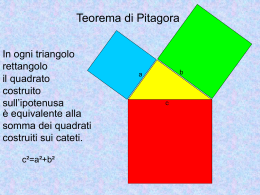
Chi era, ma soprattutto cosa ha
fatto…
Pitagora (Samo, c. 570 a.C. – Metaponto, c. 495 a.C.) è stato
un matematico, legislatore, filosofo, astronomo, scienziato e politico
greco antico secondo quanto tramandato dalla tradizione.
Pitagora viene ricordato ancor oggi per essere stato il fondatore
storico della scuola a lui intitolata nel cui ambito si svilupparono le
conoscenze matematiche e le sue applicazioni come il noto teorema di
Pitagora.
« Quanto Pitagora comunicava ai discepoli più stretti, nessuno
è in grado di riportare con sicurezza: in effetti presso di loro, il
silenzio era osservato con grande cura. »
La figura storica di Pitagora, messa in discussione da diversi studiosi, si
mescola alla leggenda narrata nelle numerose Vite di Pitagora, composte
nel periodo del tardo neoplatonismo e del neopitagorismo dove il filosofo
viene presentato come figlio del dio Apollo. Secondo la leggenda, il nome
stesso di Pitagora risalirebbe etimologicamente ad una parola che trova
il suo significato in "annunciatore del Pizio", e cioè di Apollo. Si riteneva
infatti che egli, autore di miracoli e profeta, guaritore e mago, fosse figlio
del dio stesso.
È quasi impossibile distinguere, nell'insieme di dottrine e frammenti a noi
pervenuti, non solo ciò che sicuramente appartiene al pensiero di
Pitagora ma neppure, nonostante i tentativi di John Burnet[3], di separare
il pensiero del primo da quello successivo.
pitagorismo Anche Aristotele, che possiamo considerare il primo storico
della filosofia, nella difficoltà evidente di identificare la dottrina del
maestro, parla genericamente de «i cosiddetti pitagorici» [4]
La vita di Pitagora è avvolta nel mistero. Di lui
sappiamo pochissimo e la maggior parte delle
testimonianze che lo riguardano sono di epoca
più tarda.
Alcuni autori antichi o suoi contemporanei come
Senofane, Eraclito ed Erodoto ci danno
testimonianze tali da far pensare alla effettiva
esistenza storica di Pitagora pur se inserita nella
tradizione leggendaria[6].
Secondo queste fonti Pitagora nacque nell'isola di
Samo nella prima metà del VI secolo a.C. dove fu
scolaro di Ferecide e Anassimandro subendone
l'influenza nel suo pensiero.
Da Samo Pitagora si trasferì nella Magna Grecia
dove fondò a Crotone, all'incirca nel 530 a.C., la
sua scuola. Dei suoi presunti viaggi in Egitto e a
Babilonia, narrati dalla tradizione dossografica,
non vi sono fonti certe e sono ritenuti, almeno in
parte, leggendari.
Sulla sua morte i resoconti dei biografi non
coincidono: essendo scoppiata una rivolta dei
democratici contro il partito aristocratico
pitagorico, la casa dove si erano riuniti gli
esponenti più importanti della setta fu
incendiata. Si salvarono solo Archippo e Liside
che si rifugiò a Tebe.
L'astensione dalle fave
Una versione della morte di Pitagora è collegata alla nota idiosincrasia del filosofo e della sua Scuola per le fave:
non solo si guardavano bene dal mangiarne, ma evitavano accuratamente ogni tipo di contatto con questa pianta.
Secondo la leggenda, Pitagora stesso, in fuga dagli scherani di Cilone di Crotone, preferì farsi raggiungere ed
uccidere piuttosto che mettersi in salvo attraverso un campo di fave.[9]
A proposito di questo divieto pitagorico di cibarsi di fave, Giovanni Sole nel libro Pitagora e il tabù delle fave
(Rubettino editore) ne dà un'interpretazione fisica e una spirituale. La prima è collegata al favismo che secondo
studi medici era diffuso proprio nella zona del crotonese[10], mentre la seconda fa riferimento a credenze antiche,
messe in luce da Levi Strauss, secondo cui le fave erano considerate connesse al mondo dei morti, della
decomposizione e dell'impurità (op. cit., pp. 142 e sgg.) dalle quali il filosofo si deve tenere lontano.
Il vegetarismo
Pitagora è tradizionalmente considerato l'iniziatore del vegetarismo in Occidente grazie ad alcuni versi delle
Metamorfosi di Ovidio, che lo descrivono come il primo degli antichi a scagliarsi contro l'abitudine di cibarsi di
animali, reputata dal filosofo un'inutile causa di stragi, dato che già la terra offre piante e frutti sufficienti a nutrirsi
senza spargimenti di sangue; Ovidio lega inoltre il vegetarismo di Pitagora alla credenza nella metempsicosi,
secondo cui negli animali non vi è un'anima diversa da quella degli esseri umani.[11]
Quello che modernamente conosciamo come teorema di Pitagora viene
solitamente attribuito al filosofo e matematico Pitagora. In realtà il suo
enunciato (ma non la sua dimostrazione) era già noto[1] ai babilonesi,
ed era conosciuto anche in Cina e forse in India. La dimostrazione del
teorema è invece con ogni probabilità successiva a Pitagora.
.
la somma dei quadrati
costruiti sui cateti è uguale
al quadrato costruito
sull’ipotenusa.
La dimostrazione classica del teorema di Pitagora completa il primo libro
degli Elementi di Euclide, e ne costituisce il filo conduttore. Dato che
richiede il postulato delle parallele, esso non vale nelle geoetrie noneuclidee e nella geometria neutrale. Nel testo di Euclide la dimostrazione
del teorema è immediatamente preceduta dalla dimostrazione della
costruibilità dei quadrati. L'esistenza stessa dei quadrati dipende infatti dal
postulato delle parallele e viene meno nelle geometrie non euclidee. Questo
aspetto del problema è in genere trascurato nella didattica contemporanea,
che tende spesso ad assumere come ovvia l'esistenza dei quadrati.
La dimostrazione del teorema di Pitagora consiste nel riempire uno stesso
quadrato di lato uguale alla somma dei cateti prima con quattro copie del
triangolo rettangolo più il quadrato costruito sull'ipotenusa e poi con
quattro copie del triangolo rettangolo più i quadrati costruiti sui cateti,
come in figura.
Essendo il teorema uno dei più noti della storia della matematica, ne
esistono moltissime dimostrazioni, in totale alcune centinaia, opera di
matematici, astronomi, agenti di cambio, per esempio un presidente
americano James A. Garfield e Leonardo da Vinci. Questo numero così alto
accomuna il teorema di Pitagora a quello della reciprocità quadratica[senza
fonte], per questo teorema sono state classificate dallo scienziato americano
Elisha Scott Loomis 371 differenti dimostrazioni, che sono state pubblicate
nel 1927 nel suo libro The Pythagorean Proposition.
Esiste anche una dimostrazione in forma poetica,
dell'astronomo Sir George Airy, in inglese:
"I am, as you can see,
a² + b² - ab
When two triangles on me stand,
Square of hypothenuse is plann'd
But if I stand on them instead
The squares of both sides are read."
di cui una traduzione letterale è
"Come potete vedere, sono
a² + b² - ab
Quando ci sono due triangoli sopra di me
È rappresentato il quadrato dell'ipotenusa
Ma se invece sto io sopra di loro
Si leggono i quadrati dei due lati"
I versi si riferiscono alla parte bianca: i primi due
triangoli sono quelli rossi, i secondi quelli blu.
Sia quella di Perigal che quest'ultima sono interessanti,
in quanto sono puramente geometriche, ossia non
richiedono alcuna definizione di operazioni aritmetiche,
ma solo congruenze di aree e di segmenti.
La dimostrazione attribuita al
matematico e astronomo persiano Abu'lWafa verso la fine del X secolo d.C.[2][3] e
riscoperta dall'agente di cambio Henry
Perigal (trovata nel 1835-1840[4],
pubblicata nel 1872 e successivamente
nel 1891[5]) si basa sulla scomposizione
del quadrato costruito sul cateto
maggiore, in giallo nell'immagine:
tagliandolo infatti con due rette passanti
per il suo centro, una perpendicolare ed
una parallela all'ipotenusa, si può
ricomporre in maniera da incorporare
l'altro quadrato, e formando il quadrato
sull'ipotenusa, come nella figura. Questo
procedimento è legato al problema della
trisezione del quadrato.
La scuola pitagorica, appartenente al periodo presocratico, fu fondata da Pitagora a Crotone intorno al 530
a.C., sull'esempio delle comunità orfiche e delle sette religiose d'Egitto e di Babilonia, terre che, secondo la
tradizione, egli avrebbe conosciuto in occasione dei suoi precedenti viaggi di studio.
La scuola di Crotone ereditò dal suo fondatore la dimensione misterica ma anche l'interesse per la matematica,
l'astronomia, la musica e la filosofia.
Simbolo utilizzato
dai pitagorici, come
“riconoscimento”.
Astieniti dalle fave
Non raccogliere ciò che è caduto
Non toccare un gallo bianco
Non spezzare il pane
Non scavalcare le travi
Non attizzare il fuoco con il ferro
Non addentare una pagnotta intera
Non strappare le ghirlande
Non sederti su di un boccale
Non mangiare il cuore
Non camminare sulle strade maestre
Non permettere alle rondini di dividersi il tuo tetto
Quando togli dal fuoco la pignatta non lasciare la sua traccia
nelle ceneri, ma rimescolale
Non guardare in uno specchio accanto ad un lume
Quando ti sfili dalle coperte, arrotolale e spiana l'impronta del
corpo.
(«Si noti come la regola 4 non possa logicamente coesistere
con la 7.»
La scuola, che poteva essere frequentata anche dalle
donne[2], offriva due tipi di lezione: una pubblica e una
privata.
Durante quella pubblica, seguita dalla gente comune, il
maestro spiegava nel modo più semplice possibile, così che
fosse comprensibile a tutti, la base della sua filosofia basata
sui numeri. Quella privata era invece di più alto livello e
veniva seguita prevalentemente da eletti iniziati agli studi
matematici.
Pitagora infatti aveva diviso i suoi discepoli, in due gruppi:
I matematici (mathematikoi), ovvero la cerchia più stretta
dei seguaci, i quali vivevano all'interno della scuola, si erano
spogliati di ogni bene materiale e non mangiavano carne ed
erano obbligati al celibato. I "matematici" erano gli unici
ammessi direttamente alle lezioni di Pitagora con cui
potevano interloquire. A loro era imposto l'obbligo del
segreto, in modo che gli insegnamenti impartiti all'interno
della scuola non diventassero di pubblico dominio;
Gli acusmatici (akusmatikoi), ovvero la cerchia più esterna
dei seguaci,ai quali non era richiesto di vivere in comune, o
La chiarificazione della natura dei numeri si pose
come domanda imprescindibile a Pitagora e ai suoi
seguaci. Essi si interrogarono sulle proprietà dei
numeri pari e dispari, dei numeri triangolari e dei
numeri perfetti e lasciarono un'eredità duratura
a coloro che si sarebbero occupati di matematica.
Secondo il mito, ai pitagorici si devono le seguenti
scoperte:
che la somma degli angoli interni di un triangolo è
pari a due angoli retti. Più in generale, nel caso di
un poligono di n lati la somma degli angoli interni
è uguale a 2n-4 angoli retti;
che in un triangolo rettangolo, il quadrato
costruito sull'ipotenusa è equivalente alla somma
dei quadrati costruiti sui cateti, ossia l'enunciato
(ma non la dimostrazione) del teorema noto come
teorema di Pitagora[13][14];
la soluzione geometrica di alcune equazioni
algebriche;
la scoperta dei numeri irrazionali;
la costruzione dei solidi regolari.
10 coppie di opposti, conosciuti
come opposti pitagorici:
bene e male
limite ed illimite
dispari e pari
rettangolo e quadrangolo
retta e curva
luce e tenebre
maschio e femmina
uno e molteplice
movimento e stasi
destra e sinistra
L'avanzata astronomia pitagorica è stata attribuita a Filolao di Crotone e Iceta di
Siracusa i quali pensavano che al centro dell'universo vi fosse un immenso fuoco,
chiamato Hestia: chiara la similitudine con il sole che i pitagorici si raffiguravano
come una enorme lente che rifletteva il fuoco e dava calore a tutti gli altri pianeti
che giravano attorno ad esso.
Il primo dei pianeti ruotanti è l'Anti-Terra, poi la Terra, che non è immobile al
centro dell'universo ma è un semplice pianeta, poi il Sole, la Luna, cinque pianeti
e infine il cielo delle stelle fisse. L'idea del'esistenza dell'Anti-Terra probabilmente
nasceva con la necessità di spiegare le eclissi ed anche, come sostiene Aristotele [15],
per far arrivare a dieci, il numero sacro, segno della tetrakis, dell'armonia
universale, i pianeti ruotanti intorno al fuoco centrale.
Keplero per il suo eliocentrismo si rifece, e ne diede testimonianza, alla teoria
cosmologica pitagorica che per primo concepì l'universo come un cosmo[16] un
insieme razionalmente ordinato che rispondeva anche ad esigenze mistiche
religiose.
I pianeti compiono movimenti armonici secondo precisi rapporti matematici e
dunque generano un suono sublime e raffinato. L'uomo sente queste armonie
celestiali ma non riesce a percepirle chiaramente, in quanto immerso in esse fin
dalla nascita.
Secondo Alcmeone anche l'anima umana è immortale, poiché della stessa natura
del Sole, della Luna e degli astri e, come questi si genera dall'armonia musicale di
quegli elementi opposti di cui parlerà Simmia, il discepolo di Filolao, nel Fedone
platonico.
Il divino è l'anima del mondo e l'etica nasce dall'armonia che è nella giustizia
rappresentata da un quadrato che risulta dal prodotto dell'uguale con l'uguale.
L'anima immortale dell'uomo, attraverso successive reincarnazioni, si ricongiungerà
all'anima del mondo, alla divinità ma per questo fine il pitagorico dovrà
esercitarsi alla contemplazione misterica, derivata dall'orfismo, basata sulla
sublime armonia del numero.
La vita contemplativa (bìos theoretikòs) per la prima volta assumeva nel mondo
greco un'importanza primaria.
La scoperta, tenuta segreta, delle grandezze incommensurabili, come ad esempio l'incommensurabilità
della diagonale con il lato del quadrato, causò la crisi di tutte quelle credenze basate
sull'aritmogeometria, sulla convinzione che la geometria trattasse di grandezze discontinue come
l'aritmetica.
La leggenda narra che Ippaso di Metaponto avesse rivelato questa segreta difficoltà, confermata dal
fatto che l'aritmogeometria non riusciva a risolvere i paradossi del continuo e dell'infinito che per es.
erano alla base delle argomentazioni di Zenone di Elea.
L'aritmetica e la geometria si divisero e divennero autonome.
La crisi della scuola si originava anche da motivi politici: i pitagorici sostenitori dei regimi aristocratici
che governavano in numerose città della Magna Grecia furono travolti dalla rivoluzione democratica del
450 a.C. e furono costretti a cercare rifugio in Grecia dove fondarono la comunità pitagorica di Fleio o si
stabilirono a Taranto dove con Archita rimasero fino alla metà del IV secolo a.C. A Siracusa operarono
Ecfanto e Iceta, a Tebe Filolao, Simmia e Cebete, a Locri Timeo.[