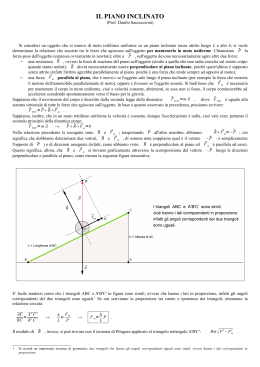
IL PIANO INCLINATO
IL MOTO LUNGO IL PIANO
INCLINATO E LE SUE COMPONENTI.
CENNI STORICI
Galileo e il piano inclinato
I contributi più importanti alla sua comprensione sono attribuiti a Galileo Galilei.
Galileo eseguì l'esperimento del piano inclinato nel 1604.
Con questo esperimento Galileo dimostra che un corpo in caduta libera si muove
di moto rettilineo uniformemente accelerato. Galileo utilizzò questo esperimento
per spiegare la caduta dei gravi, inclinando un piano per poter rallentare la
"caduta" così da poterla osservare in modo più acuto e dettagliato. Nel Seicento
per spiegare la caduta dei gravi si faceva riferimento alla teoria di Aristotele,
secondo la quale la velocità di caduta è direttamente proporzionale al peso del
corpo.
Galileo ha avuto il coraggio di mettere in dubbio ciò che diceva Aristotele, la cui
autorità all'epoca era indiscutibile.
Con l'esperimento del piano inclinato Galileo modifica radicalmente l'idea
aristotelica del moto, concentrando l'attenzione sull'accelerazione, un livello del
moto ignorato da Aristotele e dalla maggior parte dei suoi successori.
Galileo fece rotolare delle sfere lungo il piano inclinato.
In questo modo si poteva creare un'approssimazione alla caduta libera dei gravi.
Su un piano inclinato, con una pendenza minore, una palla sarebbe scesa più
lentamente, mentre sarebbe scesa più velocemente lungo un piano più ripido.
RAPPRESENTAZIONE GRAFICA
TRIANGOLI IN PROPORZIONE
Consideriamo il triangolo che rappresenta geometricamente il piano inclinato
ed il triangolo ottenuto considerando la forza peso e le sue componenti.
Questi due triangoli sono simili, in quanto hanno gli angoli ordinatamente
congruenti.
I lati corrispondenti di questi due triangoli sono in proporzione tra
loro. Quindi si potrà scrivere
P : l= P// : h
LE COMPONENTI: P,P//,P⊥
Su un corpo di massa che si muove lungo un piano inclinato liscio agisce la forza peso
perpendicolare al terreno,
(determinata da massa e accelerazione di gravità ovvero P=mg) e la forza normale
perpendicolare al piano inclinato.
La forza peso si può scomporre in due componenti, una parallela al piano (che
chiameremo P//) e una a esso perpendicolare (che chiameremo P⊥).
La prima componente si ottiene moltiplicando il modulo della forza peso per il seno
dell’angolo di inclinazione del piano .
La seconda coinvolge invece il coseno dell’angolo
L’ACCELERAZIONE
Per calcolare l’accelerazione prendiamo in considerazione l’unica forza che è
parallela al piano e quindi la componente
In questo caso l’accelerazione con cui il corpo scende lungo il piano è
completamente determinata dall’accelerazione di gravità e dall’angolo infatti:
Riassumendo, l’accelerazione con cui un corpo scivola lungo un piano inclinato senza
attrito è:
• Diretta parallelamente al piano (verso il basso)
• Direttamente proporzionale all’accelerazione di gravità g e al seno dell’angolo del
piano, ma sempre minore dell’accellerazione di gravità.
Il problema dell’equilibrio
Come può un corpo restare in equilibrio su un piano inclinato?
Se c’è abbastanza attrito ….. PUO’
Per questo prendiamo in considerazione la forza di attrito statico ( Fa ), che
mantiene il corpo in equilibrio.
Anche l’inclinazione del piano gioca un ruolo importante.
Ad ogni modo, se ci mettiamo nella condizione di ASSENZA DI ATTRITO la
risposta non può che essere:
un corpo posto su un piano inclinato non può restare in equilibrio, scivolerà
verso il basso, a meno che non venga applicata una forza equilibrante la cui
intensità dipende naturalmente dall’ inclinazione del piano stesso.
PROBLEMA (SENZA ATTRITO)
Determinare l’accelerazione di un corpo che scivola lungo un piano
inclinato senza attrito.
L’angolo che il piano forma con il suolo è di 30°.
Svolgimento:
L’accelerazione alla quale è sottoposto il corpo è espressa dalla
relazione:
a= gsenα
Sostituendo il valore di α si ha:
a= gsen30° a=4,4 m/s*.
PROBLEMA (CON ATTRITO)
Un corpo rimane in equilibrio su un piano inclinato fino a che l’angolo
di inclinazione non supera 30°. Quanto vale il coefficiente di attrito
statico tra il corpo e il piano?
Svolgimento:
Fa=kFn
Fn=P ⊥
Fa=ma
m∙a=k∙m∙g∙cos
a
gcos
4,9:(9,8 ∙0,866)= 0,6
FINE
Realizzato da
Francesca Russo
E
Flavio Nunzi