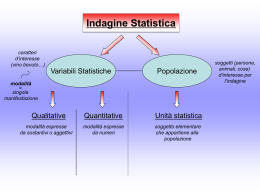
DATI E PREVISIONI
Marzo 2011
Rappresentazioni grafiche
 Cartogrammi
 Ideogrammi
 Diagrammi a torta
 Ortogrammi
 Diagrammi cartesiani
Rappresentazioni grafiche
 Cartogrammi: rappresentazione grafica nella quale il fenomeno viene
rappresentato su cartine geografiche mediante l’uso di colori o simboli.
Rappresentazioni grafiche
 Ideogrammi: rappresentazione grafica nella quale il fenomeno
viene rappresentato facendo ricorso a una particolare figura ripetuta
tante volte quant’è il valore che si vuole rappresentare.
Rappresentazioni grafiche
 Diagrammi a torta: rappresentazione grafica costituita da un
cerchio diviso in settori. L’intero cerchio rappresenta la totalità del
fenomeno mentre i settori indicano come è suddiviso il fenomeno
stesso.
Rappresentazioni grafiche
 Ortogrammi: è una rappresentazione grafica in cui i dati sono
raffigurati da rettangoli tutti di base uguale ma con altezza
proporzionale alla frequenza (numero di volte con cui un dato si
ripete).
Rappresentazioni grafiche - esercizi
 Dei 36 film in programmazione, 18 sono di fantascienza, 9 di
guerra e i rimanenti sono cartoni animati. Rappresenta
queste informazioni con un diagramma a torta
 Su 90 insetti raccolti, 45 sono formiche, 30 sono mosche, 10
sono api e i rimanenti lucciole. Rappresenta questa situazione
con un diagramma a torta.
Rappresentazioni grafiche - esempi
Il seguente ortogramma rappresenta il numero di libri letti da Mario.
 In quali mesi ha letto il minor numero di libri?
 Quanti libri ha letto a luglio?
 Quanti libri ha letto in totale?
7
6
5
4
3
2
1
0
Series1
Rappresentazioni grafiche - esercizi
Come trascorri la tua giornata? Scrivi quante ore passi in
media al giorno per:
 stare a scuola
 giocare da solo
 mangiare
 giocare con gli amici
 ascoltare musica
 fare sport
 fare i compiti
 guardare la TV
 dormire
 altro
Rappresentazioni grafiche – soluzione esercizi
9
8
7
6
5
4
3
2
1
0
s—
tare a
scuola
giocare da
—
solo
mangiare g—
—
iocare con —
ascoltare
gli amici
musica
fare sport
—
f—
are i
compiti
guardare la
—
TV
dormire
—
altro
—
Statistica
è la scienza che studia qualsiasi fenomeno di tipo collettivo,
cioè costituito da una grande quantità di oggetti che hanno almeno una
caratteristica in comune.
 Popolazione statistica: gruppo di elementi che hanno almeno


-
una caratteristica in comune
Unità statistica: è un elemento della popolazione statistica
Variabili statistiche: indicano le caratteristiche studiate ed
analizzate in statistica
qualitative, se sono esprimibili solo a parole (film preferito, titolo di
studio, …)
quantitative, se sono esprimibili con numeri (altezza, peso, età, …)
Indagine Statistica
è lo studio di un fenomeno collettivo utilizzando metodi e strumenti
matematici. Si sviluppa in 4 fasi
1. Individuare una popolazione
2. Raccogliere informazioni sul fenomeno (dati statistici)
3. Elaborare i dati
4. Interpretare quanto si è ottenuto
Esercizi…
Vuoi fare un’indagine statistica all’interno della classe per
conoscere quante ore al giorno tu e i tuoi compagni dedicate
allo studio.
1. La popolazione statistica è rappresentata da? (alunni
maschi?, tutti gli studenti della classe?, dagli insegnanti?)
2. Da chi è rappresentata l’unità statistica?
3. Da quante unità statistiche è composta la popolazione?
Esercizi…
Individua tra tutte, le variabili statistiche quantitative:
Gli sms spediti in un giorno da ogni alunno
b) Il cantante preferito da ciascun alunno
c) Il colore dei capelli di ogni alunno
d) Il peso di ogni alunno
e) I giorni di assenza di ogni alunno
f) La marca di scarpe preferite da ogni alunno
a)
Indagine Statistica
La prima fase consiste nell’individuare una popolazione.
Se la popolazione è un insieme non molto grande puoi considerare
ogni suo elemento, altrimenti devi considerarne solo una parte.
 Indagine statistica completa: quando si considera ogni
elemento della popolazione statistica
 Campione significativo: parte di popolazione statistica
selezionata per rappresentare le caratteristiche dell’intera
popolazione
 Indagine per campione: indagine in cui si considera solo un
campione significativo.
Esercizi…
Nei casi seguenti, è opportuno fare
un’indagine completa o per campione?
a) Gusto di gelato preferito dagli italiani
b) Gusto di gelato preferito nella tua classe
c) Squadra di calcio preferita nel tuo gruppo di amici
d) Squadra italiana che conta più tifosi nella tua nazione
Indagine Statistica
La seconda fase consiste nel raccogliere i dati (es. con interviste
e questionari), che devono poi essere organizzati in tabelle
e grafici (es. istogrammi, torte,…)
La FREQUENZA ASSOLUTA (f)
è il numero delle volte con cui un dato si ripete.
Esempio:
Ore di
studio
Ragazzi
1
1
1,5
2
2
8
2,5
7
3
5
1. quanti sono i ragazzi intervistati?
2. quanti ragazzi studiano 2,5 ore al giorno?
3. quale frequenza assoluta corrisponde a 3 ore
di studio?
4. quale dato corrisponde alla frequenza più alta?
Frequenza
La FREQUENZA RELATIVA (fr)
è il rapporto tra frequenza assoluta e numero di dati raccolti.
È sempre un numero compreso tra 0 e 1
Esempio:
Colore
preferito
dai clienti
Frequenza
Frequenza
relativa
Rosso
2
0,2
Bianco
2
0,2
Nero
1
0,1
Blu
5
0,5
Giallo
0
0
fr = 5/10 = 0,5 è un’informazione
completa che suggerisce al negoziante
cosa comprare. Più il valore si avvicina
a 1, più è “preferito”
Frequenza
La FREQUENZA PERCENTUALE (f%)
è la frequenza relativa per 100
f% = fr x 100
È sempre un numero compreso tra 0 e 100
Esempio:
Colore
preferito dai
clienti
Frequenza
Frequenza
relativa
Frequenza
percentuale
Rosso
2
0,2
20%
Bianco
2
0,2
20%
Nero
1
0,1
10%
Blu
5
0,5
50%
Giallo
0
0
0%
Indici di posizione
sono i valori attorno ai quali si concentrano i dati:
 MODA è il dato che ha frequenza assoluta maggiore
 MEDIA ARITMETICA può essere calcolata solo se i dati si
riferiscono a variabili statistiche quantitative. Per calcolarla devi
addizionare il valore numerico di tutti i dati e dividere il risultato
per il numero dei dati stessi:
Media = somma dati : numero dati
Indici di posizione
sono i valori attorno ai quali si concentrano i dati:
 MODA è il dato che ha frequenza assoluta maggiore
 MEDIA ARITMETICA può essere calcolata solo se i dati si
riferiscono a variabili statistiche quantitative. Per calcolarla devi
addizionare il valore numerico di tutti i dati e dividere il risultato
per il numero dei dati stessi:
Media = somma dati : numero dati
Esercizio:
calcola la media tra i dati 7, 2, 1,3, 2
7+2+1+3+2=15
15:5=3
Indici di posizione
Una variabile qualitativa si dice ordinata se i dati
che ad essa si riferiscono sono ordinabili
 MEDIANA può essere calcolata solo se i dati si riferiscono a
variabili quantitative o qualitative ordinate. Nella sequenza dei dati,
ordinati in ordine crescente, la mediana è il dato che sta in posizione
centrale se i dati sono in numero dispari, la media tra i due valori
centrali in caso di dati in numero pari.
Esercizio:
calcola la mediana tra i dati 7, 3, 5,4, 2, 1, 9
Scrivo in ordine crescente 1, 2, 3, 4, 5, 7, 9
Poiché sono in numero dispari, la mediana è il dato centrale, 4.