MODERNI IMPIEGHI DELLA STATISTICA NEGLI AMBITI
ECONOMICO, DEMOGRAFICO E SOCIALE
Torino, 28 ottobre 2002
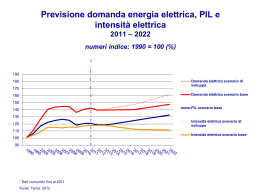
Rappresentare e simulare il
comportamento individuale con
modelli statistici: un po’ di teoria
e qualche esempio
Ugo Colombino
Baia di San Francisco
Primi anni ‘70...
• BART = Bay Area
Rapid Transit
• Introdotto nei
primi anni ‘70
Prima del BART…
Mezzi utilizzati nella Baia per recarsi al
lavoro
Rilevazione 1972
60
50
40
30
20
10
0
% uso
Auto
Bus
Carpool
55,6
23,1
21,3
Modello di scelta degli utenti
• Con i dati raccolti nel 1972 venne
sviluppato un modello econometrico
• Il modello permette di simulare la scelta
del mezzo di trasporto da parte degli
utenti
• Il modello permette anche di prevedere
la % di scelta di un mezzo non ancora
esistente nel 1972, cioe’ il BART
Uso effettivo e previsioni del modello
dopo l’introduzione del BART (1975)
60
50
40
30
20
10
0
Uso effettivo
Previsioni
Auto
Bus
Carpool
BART
59,9
55,8
12,2
14,9
21,7
22,9
6,2
6,4
Modello Logistico Multinomiale
M mezzi alternativi (1, …, M)
U(j) = “utilita’ ” del mezzo j
=V(Tempo(j), Prezzo(j), …; ) + 
= V(j; ) + 
Modello Logistico Multinomiale
Prob(  u) = exp(-exp(-u))
Distribuzione di valore estremo del
Io tipo
(Gumbel, Weibull,…)
Modello Logistico Multinomiale
Prob(U(j) = max{U(1), …, U(M)}
= exp(V(j;)/kexp(V(k;))  P(j;
)
1927 Thurnstone
1950 Marschak
1959 Luce
1968 McFadden
Stima dei parametri
Campione di N individui
jh= indice dell’alternativa scelta
dall’individuo h
Stime di Massima Verosimiglianza:
ML = argmax(hlnP(jh; ))
Specificazione empirica
V(j;) = 1TT(j) + 2WT(j) + C(j) + ...
= -0.041 TT(j) -0.147 WT(j) -2.24 C(j) + …
TT(j) = tempo di percorrenza
TW(j) = tempo casa - accesso al mezzo
C(j) = costo del percorso
1/  = disponibilita’ a pagare per un minuto in
meno di tempo di percorrenza ($ 1975)
Estate 2002, Sito Archeologico di Paestum
•
•
•
Ricerca del Dipartimento di
Scienze Economiche di
Salerno
Indagine presso circa 800
visitatori
Obiettivo: Stimare
preferenze e disponibilita’ a
pagare per caratteristiche e
servizi del sito
Esempio di scheda presentata all'intervistato, che deve indicare lo scenario preferito
Attributi
Scenario
1
SI
Scenario
2
NO
Scenario
3
NO
Audio - guide per gli scavi ed il
Museo
SI
SI
NO
Visite guidate da esperti
SI
N0
NO
Bar-caffetteria interno
NO
SI
NO
Mostre tematiche
SI
SI
NO
Eventi culturali
SI
NO
NO
per
NO
NO
NO
Proiezione audiovisivi lungo il
percorso nel Museo e negli scavi
Centro
di
documentazione
informatizzato
SI
SI
NO
NO
NO
NO
13
8
5.5
Orario di apertura prolungato
Laboratorio
didattico
bambini e ragazzi
Costo biglietto d'ingresso
Applichiamo il Modello Logistico
Multinomiale
3 scenari alternativi
U(j) = “utilita’ ” dello scenario j
=V(x1(j), …, x9(j), C(j); ) + 
Prob(U(j) = max{U(1),U(2),U(3)} = P(j)
= exp(V(j;)/kexp(V(k;))
Specificazione empirica
V(j;) = 1x1(j) + … + 9x9(j) + C(j)
xi(j) = valore dell’attributo i nello scenario j
C(j) = costo del biglietto d’ingresso nello scenario j
i/ = disponibilita’ a pagare per l’attributo i
Attributi
Parametri
stimati
Orario di apertura prolungato
0.661
(x1)
Disponibilita' a pagare
Reddito=10000
Reddito=30000
3.6
4.9
Audio - guide per gli scavi ed il
Museo (x2)
Visite guidate da esperti (x3)
0.461
2.5
3.4
0.818
4.4
6.0
Bar-caffetteria interno (x4)
-0.212
-1.1
-1.5
Mostre tematiche (x5)
0.284
1.5
2.1
Eventi culturali (x6)
0.470
2.5
3.5
Laboratorio didattico (x7)
0.718
3.9
5.3
Proiezione audiovisivi (x8)
0.491
2.7
3.6
Centro di documentazione
informatizzato (x9)
Costo biglietto d'ingresso (C ):
Reddito = 10000 Euro
Reddito = 20000 Euro
Reddito = 30000 Euro
0.408
2.2
3.0
-0.185
-0.160
-0.136