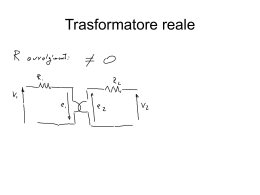
MODELLO ELETTRICO DEI
TRASFORMATORI
DEFORMAZIONE DI AVVOLGIMENTI A SEGUITO DI cto-cto
CIRCUITO EQUIVALENTE DEL
TRASFORMATORE MONOFASE
Nella ipotesi di linearità del circuito, il trasformatore monofase
può essere descritto da un doppio bipolo mediante le equazioni:
Vp   A B  Va 
 
I  = 

 p   C D  I a 
Vp = jwL p  I p + jwM  I a
Equazioni dell’equilibrio elettrico: 
Va = jwM  I p + jwLa  I a
Valori delle costanti del doppio bipolo:
A =
C =
Vp
Va
=
Ia =0
Ip
Va
Ia =0
Lp
M
1
=
jw M
B =
D =
Vp
Ia
= jw
Va = 0
Ip
Ia
M 2 - La L p
Va = 0
La
= M
M
TRASFORMATORE IDEALE
Equazioni del doppio bipolo:
 Va 
Vp   1
0
 
I  =  K
*
 p   0 -K   I a 
Caratteristica fondamentale del trasformatore ideale
è quella di trasferire le potenze senza alcun assorbimento:
(
)
N p + N a = Vp  I*p + Va  I*a = Va K  - I*a  K + Va  I*a = 0
Il circuito equivalente può quindi essere considerato come
la serie di un trasformatore ideale e di una rete passiva detta
anche “rete equivalente” del trasformatore. I parametri della
rete equivalente dipendono dalla scelta di “K” (esistono
quindi infinite reti equivalenti) e possono così essere
calcolati:
(K)
(K) *

(K)
(K)
A
1
K


B
A B A B 
0
K


K
=

=


C D  (K) (K)
*  (K)
(K) *

 C D   0 K  C

K
D
 K
La scelta del rapporto “K” è arbitraria tuttavia è opportuno
sceglierlo in maniera tale che il doppio bipolo rappresentativo
della rete equivalente risulti simmetrico; ossia in maniera tale che:
(K)
(K)
A =-D
e ciò è possibile se :
D
K K = A
*
RETI EQUIVALENTI DEL TRASFORMATORE MONOFASE
a) Rete equivalente a “”
b) Rete equivalente a “T”
CALCOLO DELLE REATTANZE DELLE RETI EQUIVALENTI
Le reattanze presenti nelle reti equivalenti del trasformatore
possono essere calcolate dalle prove a vuoto ed in cortocircuito
tenendo conto che Xcc << Xm .
a) dalla prova a vuoto
Xm
@
Vp,n
Ip,0
xm,p .u .
=
1
i0
b) dalla prova in corto circuito
Xcc =
Vp,cc
Ip,n
xcc ,p .u . = vcc
IL TRASFORMATORE IDEALE
I2
I1
U1
U2
RELAZIONI DI UN
TRASFORMATORE IDEALE
U2 = K  U1

1
I2 =  I1
K

U1I1* + U2I2* = 0

2
 Z 2 = K Z1
Tale scelta dei valori di base consente di
“eliminare i trasformatori ideali ” nei
modelli circuitali delle reti elettriche.
L’eliminazione dei trasformatori consiste
nel fatto che i valori in p.u. delle
grandezze risultano indipendenti dal lato
del trasformatore cui esse si riferiscono.
SCELTA DEI VALORI DI BASE
P
U1
1
2
Base sul lato 1
P1n = P

U1n = U1
Base sul lato 2
P2n = P

U2n = U2
U2
RELAZIONI TRA I DUE SISTEMI DI VALORI
DI BASE
P1n = P2n

1
U1n =
 U2n
K


I = P1n = K P2n = K  I
1n
2n

U1n
U2n

2
2
 Z = U1n = 1  U2n = 1  Z
2n
2
2
 1n
P1n
K P2n
K
CALCOLO DEI VALORI IN P.U.

V1
V1  K
V2
=
=
= V2u
 V1u =
U1n
U1n  K
U2n


I1
I1  K
I2
=
=
= I2u
I1u =
I1n
I1n  K
I2n


Z1
Z1  K 2
Z2
=
=
= Z 2u
 Z1u =
2
Z1n
Z 2n

Z1n  K
Nel circuito equivalente in p.u. il
trasformatore ideale è perfettamente
“trasparente” in quanto lascia inalterati i
valori in p.u. sui due lati di potenze,
tensioni, correnti e impedenze (o
ammettenze).
Ciò consentirà di descrivere un sistema
elettrico con più sottosistemi a diversa
tensione e collegati da trasformatori,
mediante una rete equivalente in p.u.
“senza trasformatori ”.
SIMILITUDINE DELLE RETI
ELETTRICHE
Due reti elettriche si dicono “simili “ quando
grandezze omogenee dell’una e dell’altra rete
sono tra loro proporzionali.
Per ogni coppia di grandezze omogenee
esisterà quindi un coefficiente di similitudine;
indicando con e senza pedice le grandezze
delle due reti dovrà valere:
SIMILITUDINE DELLE RETI
ELETTRICHE
V'
= V
V
I'
= I
I
Z'
= Z
Z
P'
= P
P
SIMILITUDINE DELLE RETI
ELETTRICHE
• Non tutti i coefficienti di similitudine possono
essere scelti ad arbitrio. Solo due sono
indipendenti (con usuale scelta dei coefficienti
di proporzionalità della potenza e della
tensione), e da essi ne derivano gli altri.
• Interessante è la similitudine “a potenza
invariante”, con coefficiente di similitudine
unitario per le potenze. In tal caso l’unico
grado di libertà è costituito dalla scelta del
coefficiente di similitudine per le tensioni.
SIMILITUDINE A POTENZA INVARIANTE
Fissato V e con P = 1 , si ottiene:
1
I =
V
Z =
2
V
SIMILITUDINE DELLE RETI
ELETTRICHE
• Una rete elettrica può essere analizzata
studiando una sua rete “simile”. Una volta
calcolate le diverse grandezze della rete
simile si potranno infine calcolare i valori
effettivi attraverso moltiplicazioni per i
coefficienti di similitudine.
I2
I1
K
R1
V1
V2
V1 = V2 /K
I1 = I2 K
R2
I1
R1
V1
I’2
K’=1
V’2
R’2
V=1/K
V1 = V2 /K = V’2
I1 = I2 K = I’2
R1
I1
I’2
V1
V’2
R’2
V=1/K
Si passa quindi ad una rete
in p.u. con una base scelta
ad arbitrio: Pn , Un
OSSERVAZIONE SUL CALCOLO DELLA RETE P.U.
PER L’ELIMINAZIONE DEI TRASFORMATORI
• Il calcolo in p.u. della rete R1 viene effettuato
direttamente utilizzando una base prefissata
che chiameremo (P1n , U1n)
• Il calcolo in p.u. della rete R2 viene
logicamente effettuato in due passi:
- passaggio ad una sua rete simile (V=1/K)
- applicazione della base prefissata.
• I due passi sono equivalenti al calcolo in p.u.
della rete R2 applicando ad essa una base
che differisce da (P1n , U1n) per il valore base
della tensione U2n = U1n K
CIRCUITI EQUIVALENTI DEI
TRASFORMATORI TRIFASI
• Trasformatori trifasi a due avvolgimenti
- banchi trimonofasi
- con nucleo a cinque colonne
- con nucleo a tre colonne
TRASFORMATORI TRIFASI
COSTITUITI DA UN BANCO DI TRE
TRASFORMATORI MONOFASE
BANCO DI TRE
TRASFORMATORI MONOFASE
TIPI DI COLLEGAMENTO
• a stella
• a triangolo
COLLEGAMENTO STELLA-STELLA
Ia1
Ip1
Ip2
Vp1
Ia2
Ip3
Ia3
Vp2
Va2
Vp3
Zp0 Za0
Va3
Va1
COLLEGAMENTO STELLA-TRIANGOLO
Ip1
Ip2
Ia1
Ia2
Va1
Vp1
Ip3
Ia3
Vp2
Va2
Vp3
Zp0
Va3
TRASFORMATORI TRIFASI CON
NUCLEO A TRE COLONNE
2
1
3
1
2
3
TRASFORMATORE TRIFASE
A CINQUE COLONNE
DETERMINAZIONE DEI
PARAMETRI DELLA RETE
EQUIVALENTE DI SEQUENZA
DIRETTA O INVERSA DALLE
PROVE DI COLLAUDO
DATI DI TARGA DI UN TRASFORMATORE
TRIFASE
• Dalla prova a vuoto (tensioni concatenate e
correnti di linea):
Vpn/Van [V]; Ip0 [A]; P0 [W]; ip0%; p0%; ip0; p0;
• Dalla prova in cortocircuito (tensioni concatenate
e correnti di linea):
Vcc [V]; Pcc [W]; vcc%; pcc%; vcc; pcc;
CALCOLO DI “Kn”
Kn
Van
=
Vpn
CALCOLO DI “Xm”
Ip0
Vpn
CALCOLO DI “Xm”
a) in valori assoluti
Vpn
3 Ip0
= Xm
X cc
+
@ Xm
2
[ ]
b) in p.u.
x m,p.u.
Vpn
3Ipn 100
Xm
1
=
@

=
=
Zb
ip0 % ip0
3 Ip0 Vpn
CALCOLO DI “Xcc”
Ipn
Vpcc
CALCOLO DI “Xcc”
a) in valori assoluti
Vpcc
3 Ipn
2X m X cc
=
@ X cc
2X m + X cc
[ ]
b) in p.u.
x cc,p.u.
Vpcc
3Ipn v pcc %
X cc
=
@

=
= v pcc
Zb
100
3 Ipn Vpn
Z
[%]
20
Y
[%]
4
16
3
12
2
8
1
4
.01
.1
1
10 100 1000 [MW]