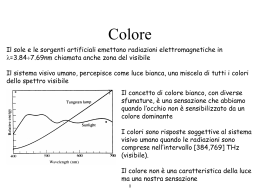
Modelli del colore
1 - Fondamenti
Daniele Marini
1
Gli attributi del colore
• Tinta - se non c’è tinta il colore è acromatico
• Saturazione - percentuale della componente acromatica di un
colore (cresce al calare di questa)
• Cromaticità - attributo della percezione del colore composto dagli
attributi tinta e saturazione
• Luminosità - si applica solo per gli oggetti che sono considerati
isolati e la luce raggiunge l’occhio solo dall’oggetto preso in
considerazione, scientificamente è meglio espressa da uno dei
seguenti attributi:
• Chiarezza - prodotta dalla presenza di un secondo stimolo e
comunemente implica una comparazione è tipica delle superfici riflettenti
• Brillanza - quantità di livello di grigio o di fluorescenza (livello di grigio
negativo) in relazione a ciò che circonda l’oggetto è tipica delle superfici
che emettono luce (sorgenti)
2
La tinta
•
•
Nella tavolozza del pittore le tinte pure sono distribuite ad
arco
Una tinta pura è:
–
–
–
un colore monocromatico dell’arcobaleno ovvero
una luce monocromatica composta da una sola lunghezza d’onda
ovvero un colore completamente saturo
Ruota dei colori
3
Saturazione
Quantità di tinta pura che deve essere mescolata al bianco per
produrre il colore percepito
Non basta la ruota dei colori, occorre una seconda
dimensione: il grigio/bianco è al centro
4
Luminosità
Intensità della luce
Non basta il cerchio dei colori, occorre una terza dimensione:
Lo spazio
dei colori
5
Sistemi di ordinamento del colore
• Atlanti colore:
–
–
–
–
Munsell
DIN 6164
OSA
NCS
• Campionari colore
– Pantone, Ral, commerciali……
6
Sistema di Munsell
(1904)
7
8
9
Munsell Book
10
Sistema di Munsell
Elegante ed intuitivo
Soggettivo
Problema:
Ambientare i colori in uno spazio oggettivo (misurabile)
con le caratteristiche positive del sistema di Munsell (intuitività)
11
Colore: fisica o psiche?
• Le teorie del colore si contrastano su due
posizioni estreme:
– Newton: il colore come stimolo di origine fisica
– Goethe: il colore come fenomeno psicofisiologico
• Edwin Land (Polaroid): tenta la sintesi con
la teoria Retinex
12
La teoria del Tristimolo
Hermann von Helmholz
1867, Heidelberg
Ottica Fisiologica
Per primo individua coni
e bastoncelli e formula la
teoria del tristimolo
Verso una definizione
matematica del colore!
13
La percezione: la retina
•
1.
2.
Le cellule che compongono la retina si suddividono in
due categorie:
I bastoncelli: sono sensibili ai livelli di luminanza
I coni: sono di tre tipi:
I. I coni sensibili alle lunghe lunghezze d’onda (rosso)
II. I coni sensibili alle medie lunghezze d’onda (giallo verde)
III. I coni sensibili alle corte lunghezze d’onda (blu)
14
Sensibilità spettrale dei coni
15
Log sensibilità spettrale dei coni
16
Altre teorie del colore
Helmholz era consapevole del problema della costanza
cromatica
Teoria dei colori opposti di Hering: 6 stimoli cromatici:
rosso, verde, blu, e tre coppie antagoniste: bianco/nero,
giallo/blu rosso/verde :
Impossibile concepire un “rosso verdastro” o un “giallo
bluastro”
17
Tristimolo: Color matching
Esperimenti di Wright (1928) e Guild (1931)
18
Risultati di Wright
(1928)
Risultati di Guild
(1931)
19
•I valori negativi delle curve indicano che in alcuni casi
occorre spostare un primario nell’area campione, il che
corrisponde a sottrarlo dal campo di test
•L’esperimento dimostra che per ottenere un colore
bastano tre primari (legge di Grassmann)
•Lo spazio dei colori è uno spazio lineare: un colore può
essere espresso come combinazione lineare dei primari.
•I primari sono stati derivati dall’esperimento W-G
definendo l’osservatore standard CIE - Commission
Internationale de l’Eclairage nel 1931
20
Tristimolo: l’osservatore standard CIE
•
1.
2.
3.
4.
Le curve ottenute da Wright e Guild furono
trasformate matematicamente per ottenerne altre
tre equivalenti in cui:
I valori negativi furono eliminati
La curva del verde fu imposta uguale a V()
Quella del blu fu posta = 0 per un ampio tratto
Per tutte e tre le curve fu imposto di avere area
sottesa uguale (ovvero pari energia)
21
Tristimolo: l’osservatore standard CIE
•
Il risultato è un tris di funzioni dette di
sensibilità dell’osservatore standard CIE
(color matching function)
x ( )
y ( )
z ( )
22
I valori di tristimolo CIE XYZ
•
Data una luce di radianza spettrale (colore)
Le() si ottengono i valori di tristimolo X Y
Z dalle formule (dove K(555) =
Kmax=683lm/W)

Y  K (555 ) 
Z  K (555 ) 
X  K (555 )
780
380
780
Le ( )  x ( )d
Le ( )  y ( )d
380
780
380
Le ( )  z ( )d
23
L’osservatore standard CIE
•
•
I valori di tristimolo corrispondono ad una misura
numerica di tinta, saturazione e luminosità?
Risposta:
– Y è la luminanza Lv (luminosità)!! Infatti:
780
Y  K max
780
 L ( ) y ( )d   L ( ) K
e
380
e
380
max
V ( )d 
780
 L ( ) K ( )d  L
e
v
380
– X e Z purtroppo non sono tinta e saturazione
•
I ricercatori cercarono di ottenere i valori di tinta e
saturazione con un passaggio ulteriore
24
Lo spazio del colore CIE
•
Nello spazio colore X Y Z dei valori di
tristimolo si osserva sperimentalmente che tutti i
colori percepibili stanno dentro un cono
deforme
25
Le coordinate cromatiche CIE
•
•
X+Y+Z=1 è l’equazione di un piano su
cui la luminanza è costante
Dai valori di tristimolo X Y Z si ottennero
le coordinate cromatiche x y z tramite la
trasformazione:
X
Y
Z
x
; y
; z
X Y  Z
X Y  Z
X Y  Z
26
Il diagramma di cromaticità CIE
•
x e y sono le
coordinate di un
sistema cartesiano su
cui si rappresenta una
sezione del cono dei
colori a prescindere
dalla luminanza Y: Il
diagramma di
cromaticità CIE
27
Definizione matematica del colore (x y Y)
•
•
•
x e y non sono purtroppo tinta e saturazione,
tuttavia
Tramite il diagramma di cromaticità da x e y si
ottengono la tinta e la saturazione
Quindi un colore risulta completamente definito
dalla tripletta di valori (x y Y): coordinate
cromatiche più luminanza
A partire dalle terna (x, y, Y) è possibile ricavare i valori di
tristimolo X, Y e Z attraverso le relazioni:
X = x Y/y , Y = Y, Z = (1- x - y) Y/y
28
Proprietà diagramma CIE
• Linearità
• Purezza
• Lunghezza d’onda
dominante
• Lunghezza d’onda
complementare
• Colori complementari
29
Problema: Metamerismo
30
Problema: Metamerismo
Non esiste corrispondenza biunivoca tra
distribuzione spettrale di radianza e valori di
tristimolo
Le ( )
X   Le ( ) x ( )d
Y   Le ( ) y ( )d
Z   Le ( ) z ( )d
31