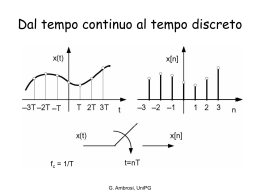
Equazioni di analisi e sintesi
(segnali periodici a tempo continuo)
Analisi
Sintesi
(nota: X_k è in generale complessa)
G. Ambrosi, UniPG
Segnali aperiodici a tempo continuo
G. Ambrosi, UniPG
Cosa succede alla serie di Fourier e ai relativi coefficienti Xk quando To ->?
G. Ambrosi, UniPG
Spettro di ampiezza di xp(t)
G. Ambrosi, UniPG
To   (1)
Definiamo:
Passando al limite per To  
G. Ambrosi, UniPG
To   (2)
To   kfo – (k-1)fo = fo  0
Definiamo:
G. Ambrosi, UniPG
To   (3)
Passando al limite per To  
Trasformata continua di Fourier del segnale x(t)
Spettro di fase
Spettro di ampiezza
G. Ambrosi, UniPG
Equazione di sintesi
Segnale periodico
Segnale aperiodico
G. Ambrosi, UniPG
Equazioni di analisi e sintesi
segnali continui
Eq. di analisi
Eq. di sintesi
G. Ambrosi, UniPG
Teoremi (proprietà) della trasformata di
Fourier
Teorema della linearità:
Teorema di dualità:
Teorema del ritardo:
G. Ambrosi, UniPG
Filtri (?)
G. Ambrosi, UniPG
G. Ambrosi, UniPG
Passiamo al dominio frequenziale
Abbiamo bisogno di un apparato con caratteristiche di
selettività delle differenti componenti frequenziali
del segnale: un filtro
G. Ambrosi, UniPG
Dal tempo continuo al tempo discreto
fc = 1/T
G. Ambrosi, UniPG