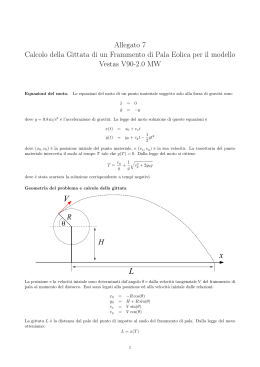
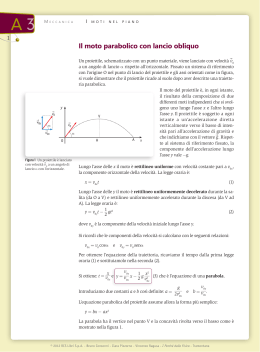
CONSIDERAZIONI SULLA
DIVULGAZIONE
ESEMPIO DI
SEMPLIFICAZIONE
DIDATTICA:
IL MOTO PARABOLICO DEI
GRAVI
IL PROGRESSO DELL’ERA MODERNA
RICHIEDE:
• Continui aggiornamenti dei mestieri e delle
professioni;
• Conoscenze scientifiche per operare scelte
decisive nella società;
• Trasferimento tecnologico e prodotti di
qualità per rendere competitive le aziende.
I GIOVANI
• Intendono utilizzare l’apprendimento in
situazioni concrete;
• Disertano alcune facoltà scientifiche perché
offrono ridotte prospettive di lavoro (si
rischia nel futuro di rendere incontrollabili
le conoscenze già acquisite).
LA RICERCA
• Pubblica dispone di fondi insufficienti;
• Privata viene svolta in poche aziende,
perché le altre (PMI) sono orientate soltanto
verso la produzione.
LE TEORIE SCIENTIFICHE AVANZATE
• Sono complesse ed ampie;
• Contengono una mole enorme di
conoscenza ancora da tramutare in
applicazioni utili.
NELLA SCUOLA SUPERIORE SI
INSEGNA POCO LA FISICA MODERNA
PER
•
•
•
•
•
Difficoltà intrinseche;
Costi proibitivi delle apparecchiature;
Sistemazione parziale della didattica;
Carenze in vari programmi ministeriali;
Esiguo numero di ore per l’insegnamento
della materia.
LA DIVULGAZIONE SCIENTIFICA PUO’
•
•
•
•
•
•
•
•
•
Rendere comprensibili le concezioni portanti della teoria;
Svegliare l’interesse dei giovani;
Soddisfare la curiosità delle persone;
Fornire importanza alla scienza;
Servire a tutti, anche al ricercatore che vuole avvicinarsi ad
altri settori del sapere;
Favorire la ricerca;
Snellire alcune procedure fruibili con competenze
adeguate;
Essere didattica;
Essere popolare, scorrevole, correlata.
PER LA DIVULGAZIONE DIDATTICA
DELLA FISICA MODERNA
• Esiste molto materiale, ma manca un
orientamento unitario;
• Diverse spiegazioni sono qualitative perché
il formalismo è improponibile.
NELLA DIDATTICA DELLA FISICA
CLASSICA
• Si trovano svariate applicazioni nella vita
quotidiana da interpretare;
• Gli studenti si pongono molti quesiti desueti;
• Si possono eseguire ed escogitare tanti esperimenti;
• Vi sono diversi problemi esterni e interni ai
programmi da risolvere;
• Alcuni concetti si possono semplificare, ma questo
comporta spesso l’esplorazione di numerosi
percorsi;
• Se i risultati diventano possibili e facili, si ottiene
un progresso nella razionalità ed un agevolazione
all’apprendimento.
MOTO PARABOLICO DEI GRAVI
SEMPLIFICAZIONE
• Fenomeno comune;
• Trattato nei testi del biennio in modo discorsivo;
• Utilizza la trigonometria (duplicazione generata
dall’addizione);
• Nei licei la trigonometria viene trattata
successivamente;
• Si possono esperire percorsi alternativi istruttivi ed
equivalenti.
COMPOSIZIONE DEGLI SPOSTAMENTI
L
y
g t2 /2
Vo

S
O
t
S po s tam en t i
pa rz ai li
to at el
o
t
n
e
po s tam
x
A
COMPOSIZIONE DELLE VELOCITA’
TRAIETTORIA PARABOLICA DI UN GRAVE
L’EQUAZIONE DELLA PARABOLA
CONSERVA LA SUA FORMA
s  v 0t
1
z  gt 2
2
gs2
z
2
2v 0
• s = percorso nella direzione di lancio;
• z = percorso nella direzione verticale.
AL VARIARE DEL PUNTO DI TANGENZA,
CAMBIA SOLTANTO Vo.
• LA MATEMATICA VIENE UTILIZZATA
PER SPIEGARE I FENOMENI FISICI;
• LA FISICA PUO’ SUGGERIRE NUOVI
PROCEDIMENTI MATEMATICI.
LO STESSO RISULTATO SI PUO’
OTTENERE CON METODI ANALITICI
IN COORDINATE CARTESIANE:
 Ricavando il coefficiente angolare della
tangente;
 Scrivendo l’equazione della tangente;
 Sottraendo le ordinate della tangente e della
parabola.
LA PROCEDURA FISICA RISULTA PIU’
IMMEDIATA PERCHE’ BASATA SULLA
TANGENZA DELLA VELOCITA’ ALLA
TRAIETTORIA.
L’EQUAZIONE DELLA PARABOLA
RIMANE INVARIATA
x  v 0x t
1
z  gt 2
2
g x2
z
2
2v 0x
• x = ascissa dal punto di tangenza;
• z = segmento verticale tra parabola e tangente.
CAMBIANDO IL PUNTO DI CONTATTO, Vox
RISULTA COSTANTE.
VERIFICA DELLA PROPRIETA’ PER ALCUNE
TANGENTI DELLA PARABOLA y = 4x – x^2
DALLA TANGENTE ORIZZONTALE SI
OSSERVA CHE:
o La curva è simmetrica rispetto al suo asse
verticale;
o I tempi di salita e discesa sono uguali.
DALLA TANGENTE INIZIALE DERIVA
CHE:
 I tempi suddetti valgono Voy/g;
 L’altezza massima (Voy)²/(2g) cresce con
l’angolo di tiro.
OB  AD Vo t  AD 2Vo  AD 2Vo  GE 2Vo  c
Gittata  OA 




2
AB
gt
g
g
gt / 2
LA GITTATA E’ PROPORZIONALE A “c”. DIVENTA
MASSIMA PER c = Vo/2 ED UN ANGOLO DI TIRO
DI 45°.
Vo
c
Vx
Vo
45 °
45 °
Vo
/2
A
ng
o
lid
i ti
ro
ANDAMENTO DELLA GITTATA CON
L’ANGOLO DI TIRO
Vo
METODO ALGEBRICO
Per Vox = Voy, cioè per un lancio a 45°, la
gittata è massima.
2 Vo  c  2 Vox  Voy  Vox  Voy  ( Vox  Voy ) 
2
 Vo  ( Vox  Voy )
2
2
2
2
TRAIETTORIE PER ANGOLI DI LANCIO DI
15°, 30°, 45°, 60°, 75°
APPLICAZIONE DEL 1° TEOREMA DI
EUCLIDE
s 2 Vo  t 2


2
z gt /2
2
B
s
2
2Vo

 BN 
g
 cos tan te
QUESTA COSTANTE
PERMETTE DI
CONSIDERARE LA
GITTATA COME UNA
SEMICORDA DELLA
STESSA
CIRCONFERENZA.
z
O
A
N
CONSEGUENZE DIRETTE
LA GITTATA:
•SI PUO’
MISURARE;
•CRESCE FINO AD
UN ANGOLO DI
TIRO DI 45° E POI
DIMINUISCE;
•AL MASSIMO E’
IL RAGGIO.
CONSEGUENZA DIRETTA
LA GITTATA E’ LA
STESSA PER
ANGOLI
COMPLEMENTARI.
CONSEGUENZA DIRETTA
L’ALTEZZA
MASSIMA
AUMENTA CON
L’ANGOLO DI
LANCIO.
VERIFICHE POSSIBILI CON UN GETTO
D’ACQUA
•
•
•
•
CONTINUITA’ DELLA TRAIETTORIA;
FORMA DELLA CURVA;
VARIAZIONE DELLA GITTATA;
MASSIMA QUOTA.
PASQUALE CATONE
ITIS-LS IOANI
CASETA