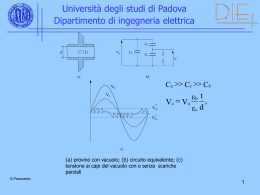
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Correnti di elevato valore
• DC - HVDC – Galvaniche
Shunt – Accoppiamento galvanico
Misuratori ad effetto HALL
• AC – Impianti AC, spesso bt
TA – offrono separazione galvanica
Problemi di non linearità nel caso di prove di breve durata
• Impulsive
• Prove su scaricatori
• Studio effetti correnti di fulmine
G.Pesavento
1
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Generazione di impulsi di corrente
Forme d'onda
Prove sugli scaricatori
Impulsi di corrente di grande ampiezza (da 1 a 100 kA)
Le forme d'onda più caratteristiche si distinguono in onde impulsive
doppio-esponenziali, simili agli impulsi di tensione ma con minor
rapporto fra la durata all'emivalore e la durata del fronte (onde 1/20,
4/10, 8/20, 30/80 s etc.
Onde rettangolari, con durate dell'ordine delle migliaia di s; le
ampiezze di queste ultime, nell’ambito delle prove sono, di norma,
relativamente basse (qualche centinaio di A).
Per tutte queste forme d'onda, la normativa fornisce le definizioni e le
tolleranze in modo analogo a quello adottato per le tensioni. La durata
del fronte viene determinata sui punti al 10 e al 90% (T1=1,25 T); sui
parametri temporali e sul valore di cresta la tolleranza è tipicamente del
10%.
G.Pesavento
2
Università degli studi di Padova
Dipartimento di ingegneria elettrica
1,0
B
0,9
0,5
0,1
C
0
O1
T
T1
T2
1,0
0,9
Td
0,1
0
Tt
G.Pesavento
3
Università degli studi di Padova
Dipartimento di ingegneria elettrica
L
E
R
C
SH
i
Schema di generatore di correnti impulsive
G.Pesavento
4
Università degli studi di Padova
Dipartimento di ingegneria elettrica



t  C
1
2
i( t )  exp(  ) E

sin ωn t 1  z 
T  L 1  z2

z=
R
2
C
L
ωn 
L
VC
1
LC
T=2L/R.
R
C
i
G.Pesavento
5
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Circuito per la generazione di correnti impulsive
G.Pesavento
6
Università degli studi di Padova
Dipartimento di ingegneria elettrica
i (t)
vm(t)
Rm
Zo
Circuito per la misura di una corrente i(t)
G.Pesavento
7
Università degli studi di Padova
Dipartimento di ingegneria elettrica



t  C
1
2
i( t )  exp(  ) E

sin ωn t 1  z 
T  L 1  z2

z=
R
2
C
L
n
L
VC
=
1
LC
T=2L/R.
R
C
i
G.Pesavento
8
Università degli studi di Padova
Dipartimento di ingegneria elettrica
i (t)
i (t)
Rm
Rm
C
vm (t)
L
vm (t)
L
Influenza degli elementi parassiti
G.Pesavento
9
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Le dimensioni dello shunt sono determinate dal
sovrariscaldamento permesso, essendo diverse le
considerazioni da fare nel caso di shunt per la misura di
correnti alternate ed impulsive.
Es. shunt di 0,1  per 500 A efficaci; la potenza dissipata
è di 2500 W e richiederà un raffreddamento forzato.
Nel caso di shunt per correnti impulsive si può invece
trascurare la trasmissione di calore all'esterno e
considerare il riscaldamento adiabatico.
Ciò comporta, fissato la massima temperatura
ammissibile, un minimo per il volume dello shunt.
G.Pesavento
10
Università degli studi di Padova
Dipartimento di ingegneria elettrica

W   Ri 2 dt  cγvΔθ
da cui
v  W/cγθ
o
dove v è il volume,  rappresenta il salto di temperatura, c il calore specifico
e  il peso specifico del materiale.
E’ quindi possibile che gli shunt debbano essere massicci, con problemi legati
allo spessore di penetrazione.
G.Pesavento
11
Università degli studi di Padova
Dipartimento di ingegneria elettrica
i
r
i
vm
i
d
i
i
l
Shunt coassiale
G.Pesavento
ρl
R
2 πrd
12
Università degli studi di Padova
Dipartimento di ingegneria elettrica
i (t)
vm(t)
Rm
Zo
Circuito per la misura di una corrente i(t)
G.Pesavento
13
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Nell'ipotesi che sia d«r, la densità di corrente sulla
superficie interna varia nel tempo con la legge


 n 2 t 
n

G  G o 1  2  1 exp  
 T 

n 1


Io
Go 
2πrd
G.Pesavento
e T
μd 2
π 2ρ
14
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Risposta normalizzata di shunt coassiale
1
0.9
0.8
0.7
[g]
0.6
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
[t/T]
6
7
8
9
10
Risposta normalizzata ad un gradino di shunt coassiale
G.Pesavento
15
Università degli studi di Padova
Dipartimento di ingegneria elettrica
La tensione misurata vale:
2 



n
t
n

Vt   ρ1G  RI o 1  2  1 exp 
 T 

n 1


La costante di tempo generalizzata vale:


2 

n
t
To   η t  dt    2  1n exp  
dt
 T 


o
o n 1

 1n
n 1
n2
 2T 
G.Pesavento

 π 2  μd 2

 2T 
 12  6


16
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
17
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Shunt a gabbia – 250 kA
G.Pesavento
18
Università degli studi di Padova
Dipartimento di ingegneria elettrica
i(t)
vi(t)
Sonda di Rogowski
vi (t) = M di(t)/dt
G.Pesavento
19
Università degli studi di Padova
Dipartimento di ingegneria elettrica
vi(t)
i2(t)
Z0
~
L
R
Z0
Vm(t)
Rs
ωL >> R+Rs
di 2
vi(t)=L
dt
v m  Ri 2 
G.Pesavento
1
da cui i 2 =  vi (t)dt
L
R
R
v
(
t
)
dt

Mi1 ( t )

L i
L
20
Università degli studi di Padova
Dipartimento di ingegneria elettrica
vi(t)
Z0
~
L
R
Z0
C
Vm(t)
ωRC>>1 limite inferiore
ωL << Z limite superiore
vm 
G.Pesavento
1
RC
 v i (t )dt 
M
i1 ( t )
RC
21
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Sonda di Rogowski
FESSURA
RIVESTIMENTO
DI ALLUMINIO
BOBINA DI
ROGOWSKI
IN RESINA
RESISTENZA
DI CARICO
G.Pesavento
r
d
a
22
Università degli studi di Padova
Dipartimento di ingegneria elettrica
A
v
G.Pesavento
23
Università degli studi di Padova
Dipartimento di ingegneria elettrica
z
Sz
Sy
Sx
x
G.Pesavento
y
24