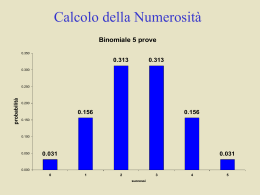
4) DISTRIBUZIONI
NOTEVOLI
4.1) La v.c. Binomiale
Caratteristiche dello spazio campionario
La v.c. Binomiale è utile quando l’esperimento casuale
presenta le 3 caratteristiche seguenti:
1. Si estrinseca in un numero finito n di prove fra loro
indipendenti;
2. Ciascuna prova può avere 2 soli esiti necessari ed
esaustivi, ad esempio “Successo” ed “Insuccesso”;
3. È nota la probabilità  del successo e tale probabilità
è costante per tutte le n prove.
Il corrispondente spazio campionario  contiene eventi
elementari che sono delle n-uple composte da un numero
x di Successi ed (n - x) Insuccessi.
Valori e f.p.
Sia X = “n. di successi sulle n prove indipendenti”, allora
i valori di X sono x = 0, 1, …, n cioè X è v.c. discreta e
la sua f.p. è:
 n x
n x
P X  x        1   
 x
Dove:
(1 - ) rappresenta la probabilità dell’Insuccesso (evento
complementare del Successo).
 n
 
 x
è il coefficiente binomiale che conta il
numero di n-uple che, fra tutte quelle che possono
presentarsi, contengono x Successi ed (n - x) Insuccessi in
qualunque ordine.
X è detta v.c. Binomiale con parametri n (numero delle
prove indipendenti) e  (probabilità di Successo);
brevemente si scrive: X  Bin (n, ).
Valore atteso e varianza della v.c. Binomiale
Se si immagina di ripetere n volte indipendentemente la
prova che ha dato origine alla v.c. di Bernoulli, allora la
v.c. Binomiale è data dalla somma di n v.c. Bernoulliane
identiche, brevemente si scrive
n
X  Binn,     X i
i 1
con
Xi  Bern 
indipendenti.
Da tali considerazioni si possono ricavare la media e la
varianza di una Binomiale:
n
 n
 n
  E  X   E   X i    E  X i     n
 i1  i1
i 1
 n

  V X   V   Xi  
 i1 
2
n
n
i 1
i 1
per
l’indipendenza
 V  X i     1     n 1   
4.2) V.c. di Bernoulli
Nel caso particolare di un’unica prova, la v.c. X  Bin (n
= 1, ) è detta v.c. di Bernoulli, brevemente si scrive X 
Bern (), e ha f.p.
P X  x    x  1   
1 x
o anche più esplicitamente:
x
p(x)
0
(1-)
1

Media e varianza della v.c. di Bernoulli sono:
1
  E  X    x  p x   0  1     1   
x 0
1
 2  V  X   E  X       x   2  p x  
2
x 0
 0     1     1         (1   )
2
2
4.3) Distribuzione
uniforme (o
rettangolare)
Nel discreto, si dice “uniforme” una variabile
casuale che assume i valori di cui è suscettibile con
probabilità (o frequenze) tutte uguali a 1/n. Nel
continuo, è una variabile dotata di densità costante
entro il suo campo di esistenza.
La rappresentazione nel discreto è il seguente
diagramma a canne:
1/n -
1
2
3
4
n
Nel continuo si ha il seguente istogramma:
1/(b-a) -
a
b
La distribuzione cumulativa (schema di
ripartizione) si esprime, in campo discreto,
nella seguente “gradinata”:
1-
0
1
mentre è descritta, nel continuo, dal seguente
grafico:
1-
a
b
I valori notevoli della funzione di densità
f(x)=1/(b-a)=C sono:
1) per x<a:
f(x)=0
2) per a<x<b:
f(x)=C=1/(b-a)
4.4) La v.c. casuale
normale (o Gaussiana)
È la più importante fra le v.c. continue perché si presta a
ben interpretare molti fenomeni statistici reali.
Caratteristiche della v.c. normale
1. Assume tutti i valori reali x  , cioè
- < x < +.
2. È caratterizzata da 2 parametri  e 2 che coincidono
con la media e la varianza di X, cioè  = E(X) e 2 = V(X),
brevemente si scrive XN(, 2).
3. La f.d. (x) di X ha forma “campanulare”, simmetrica
rispetto a  e cambia concavità nei punti x =  -  e x = 
+  (flessi); graficamente:
(x)



x
4. (x) è f.d., quindi l’area sottesa alla campana
rappresenta la probabilità di X. L’area totale è 1.
5.  rappresenta anche la moda di X (punto a maggior
densità di probabilità) e la mediana di X ((x) è
simmetrica rispetto a , cioè P(X) = P(X) = 0.5).
6. Variazioni del valore di  rappresentano “traslazioni”
(movimenti orizzontali) di (x). Cioè: dati 1< 2< 3 e
2 fisso, graficamente si ha:
  N ( 2 /  2 )
  N ( 1 /  2 )
  N (3 /  2 )
(x)
1
2
3
x
7. Variazioni del valore di 2 rappresentano variazioni
nella forma di (x) (innalzamento o appiattimento). Cioè,
dati 12 < 22 < 32 e  fisso, graficamente si ha:
  N ( /  1 )
2
  N ( /  2 )
2
(x)
  N ( /  3 )
2

x
e l’area totale sottesa alle curve sempre pari a 1.
8. Come per tutte le v.c. continue, dati due numeri a e b
con a < b si ha:
P(a < X < b) = area sottesa a (x) nell’intervallo (a,b) =
(b) - (a).
(b)- (a)=P(a<X<b)
(b)
(x)
(x)
(x)
(a)
ab 
x
ab 
x
ab
x
Standardizzazione e v.c. Normale standardizzata
La “standardizzazione” è un’operazione che si effettua
sulla v.c.. Consiste nel sottrarre alla v.c. la sua media  e
dividerla per la radice quadrata della sua varianza  =
scarto quadratico medio.
La standardizzazione ha l’effetto di rendere la media nulla
e la varianza unitaria. La standardizzazione è un caso
particolare di trasformazione lineare.
Se si effettua la standardizzazione su una v.c. XN(, 2)
si ottiene la v.c. Normale standardizzata:
X 

 Z  N 0,1
con:
X 
 1 




E Z   E 
  E    X   E   
  
  

 
1
 1
 
 E   X      E  X      0
 
 


X 
   1  X  V   
V Z   V 

V





  
  

 
1
1
1


 V   X   0  2 V  X   2   2  1




Le tavole della Normale standardizzata
La v.c. ZN(0,1) è v.c. Normale e come tale possiede le
caratteristiche descritte. Inoltre la f.r. (z) di ZN(0,1) è
stata completamente tabulata. Dalla tavola 1 (tratta da: S.
Kokoska - C. Nerison “Statistical Tables and Formulae”;
Springer - Verlag, 1988) si possono ricavare le seguenti
informazioni:
• La prima colonna a sinistra intestata ai valori z riporta le
prime 2 cifre dei valori delle v.c. ZN(0,1) compresi tra 0 e
3.4.
• La prima riga in alto (anch’essa intestata ai valori z)
riporta la seconda cifra decimale da accostare alle prime 2
cifre per ottenere un valore z composto da una cifra intera e
2 cifre decimali.
•All’interno della tabella sono riportati i valori della f.r.
(z)delle v.c. ZN(0,1). Ad esempio, all’incrocio fra la 5°
riga e la 4° colonna, cioè in corrispondenza del valore z =
0.42, si legge: (z) = (0.42) = 0.6628.
(x)
(z)=P(Z<z)
z
x
Le tavole della Normale standardizzata possono essere
utilizzate:
• in via diretta per determinare la probabilità di un
intervallo (a,b) di qualunque v.c. XN(,2).
La regola generale:
a X  b

Pa  X  b   P




 
 
a
b
b
a



 P
Z
  
  
.
 
 
  
  
Si cercano sulle tavole i valori z=(a-)/ e z = (b -)/ e
si leggono i valori  corrispondenti all’interno delle
tavole.
• in via indiretta per determinare il valore x di una
qualunque v.c. X~N(,2) corrispondente ad una data
probabilità p, cioè tale che:
P(Xx) = (x) = p
con 0<p<1
la regola generale è:
X  x

p  P  X  x   P


 
 
x
x
 P Z 





 

  
con p noto e x incognita.
All’interno delle tavole si cerca il valore p e all’incrocio
della riga e della colonna corrispondenti si legge il valore
zp.
Si pone zp = (x-)/ e si ha: x = zp·  + .
• le tavole non riportano valori z negativi (z<0) perché si
possono ottenere da quelli positivi sfruttando la simmetria.
La regola generale è:
(-z) = 1- (z) e (z) = 1- (-z)
Graficamente:
(x)
1(-z)
(-z)
-z
0
z
x
Esempio: il peso di un neonato può essere
interpretato come una v.c. Normale con media
=3 kg e scarto quadratico medio =0.5 kg. Si è
interessati a conoscere la probabilità che, scelto a
caso un neonato fra quelli del reparto maternità di
un ospedale, questo abbia peso “regolare”, cioè
compreso tra 2.7 e 3.7 kg.
Sia X la suddetta v.c. Normale interprete del peso.
La probabilità richiesta risulta P(2.7<X<3.7).
Procedendo alla standardizzazione e consultando
la tavola 1 si ottiene:
2.7  3
3.7  3
Z
)
0.5
0.5
P(0.6  Z  1.4)  (1.4)  (0.6) 
P(2.7  X  3.7)  P(
 0.91924  0.27425  0.64499