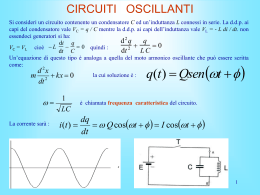
Esercizio 1
Un condensatore piano di area A=40 cm2 e distanza tra i
piatti d=0.1 mm, e` stato caricato collegandolo
temporaneamente ad un generatore di fem di 1000 V.
a) Trovare la ddp ai capi del condensatore dopo che la
distanza tra i piatti e` stata portata a 2d.
b) Trovare il lavoro speso nell’allontanamento dei piatti.
c) Determinare se il lavoro e` stato fatto dal campo o contro
il campo.
Infine si inserisce tra i piatti una lastra di materiale
dielettrico di area A, spessore 2d e costante dielettrica
relativa uguale a 2.
d) Trovare il nuovo valore della capacita`,
e) il lavoro speso per inserire la lastra e
f) determinare se il lavoro e` stato fatto dal campo o contro
il campo.
• Soluzione dell’esercizio 1
•
Troviamo innanzitutto la capacita` del condensatore:
0 A
8.85 10 12  40 10 4
C1 

 354 pF
3
d1
0.110
•
e la carica accumulata
Q  C1V1  354 1012 103  354 109 C
•
Dopo la separazione dei piatti la capacita` diviene:
C2 
•
0 A
1
 C1  177 pF
2d1 2
Per trovare la nuova ddp ci basiamo sul principio di
conservazione della carica. Cioe` la carica rimane
costante nel processo:
Q 354 10 9
V2 

 2000V
12
C2 177 10
•
Per calcolare il lavoro, il metodo piu` naturale
sembrerebbe quello di usare la sua definizione di
integrale della forza per lo spostamento.
 
  F  ds
f
L12
i
•
c’e` pero`una difficolta`: non sempre e` facile conoscere
l’espressione della forza. Vedi l’approfondimento 1 per
maggiori dettagli.
•
Il lavoro speso nell’allontanamento dei piatti si puo`
calcolare piu` semplicemente usando il principio di
conservazione dell’energia: il lavoro e` uguale alla
variazione di energia elettrostatica (cambiata di segno)
tra stato finale e stato iniziale:
L12  U 2  U1 
•
L’energia iniziale e finale sono:
1
1
U1  QV1  354 10 9 103 
2
2
 177 10 6 J
1
1
U 2  QV2  Q 2V1  QV1  2U1
2
2
•
Il lavoro e` dunque:
L12  U1  177 106 J
•
Il segno negativo significa che il lavoro e` stato fatto
contro il campo.
•
l’inserimento del dielettrico cambia il valore della
capacita`:
0 A
C1
C3   r
  r C2   r
 C1
2d1
2
•
Il lavoro compiuto si trova di nuovo mediante il principio
di conservazione dell’energia. Per l’approccio alternativo
che fa uso della forza, vedi l’approfondimento 2.
L2 3  U 3  U 2 
•
L’energia dello stato 3 e`:
1 Q2 1 Q2
U3 

 U1
2 C3 2 C1
•
E quindi il lavoro e`:
L2  3  U1  177 10 6 J
•
Il segno positivo significa che il lavoro e` stato fatto dal
campo.
• Approfondimento 1
•
Consideriamo la forza che il piatto positivo esercita su
quello negativo. L’espressione della forza che viene
spontaneo scrivere e`:
F   EQ 
•
V
Q
QQ
Q   Q   
d
dC
0 A
Ove E e` il campo elettrico nel condensatore.
Riscriviamo il campo come somma dei campi dovuti al
piatto positivo e a quello negativo:
F  E  E Q  EQ  EQ
•
•
E` evidente da questa espressione che il secondo
termine non puo` comparire, in quanto significa che il
piatto negativo eserciterebbe una forza su se stesso.
L’espressione corretta e`:
F  EQ
•
Per la simmetria tra i piatti, il campo dovuto al piatto
positivo e` meta` del campo totale, quindi:
F  
1 Q Q
2 0 A
• Alternativamente consideriamo la superficie di
Gauss tratteggiata in giallo in figura. Le zone in
colore rosso e blu rappresentano l’estensione
lungo x (molto piccola) delle cariche sui piatti.
+
-
x
• Il campo sulla base A della superficie di Gauss
contenuta nel piatto negativo e` dovuto a tutte le
cariche positive piu` una parte delle cariche
negative contenute entro tale superficie. Il flusso
sulla base si scrive:
 E ( x )   E ( x ) A 
Q  q ( x)
0
•
La forza e` dunque:
x
x
x
Q
q ( x)
F    E ( x)dq ( x)    dq ( x)   
dq ( x)
A 0
A 0
0
0
0
x
Q
1 1 2 
Q Q 1 Q2

Q 
q ( x )  


A 0
A 0  2
A 0 2 A 0
0
Q2 1 Q2
1 Q2



A 0 2 A 0
2 A 0
•
•
E` da notare che la forza e` indipendente da x. Inoltre e`
diretta nel verso x negativo e un aumento della distanza
tra i piatti (spostamento del piatto negativo nel verso x
positivo) comportera` un lavoro negativo.
Il lavoro e` quindi:
f


  F   dx    F  dx   F   x2  x1 
f
L1  2
i
i
1 Q2
1 Q 2 x2 1 Q 2 x1
x2  x1   


2 A 0
2 A 0 2 A 0
1 Q2 1 Q2


2 C2 2 C1
•
Cioe` esattamente uguale al valore ottenuto con la
conservazione dell’energia.
• Approfondimento 2
•
Consideriamo la lastra di dielettrico mentre entra nel
condensatore. Il campo elettrico al bordo
(rappresentato dalle linee nere) e` tale da indurre forze
(frecce viola) con risultante diretta verso il
condensatore. Queste forze sono responsabili del moto
del dielettrico, cosa che ci dice anche che il lavoro
sara` positivo.
+
---------- ------------+++++++++++++++++++
-
•
In questo caso non e` semplice scrivere la forza, per
cui il metodo della conservazione dell’energia si
impone.
Esercizio 2
Calcolare la ddp tra i punti A e B del circuito seguente
A
2V
3W
3W
6W
12W
8V
2W
B
2W
2V
• Soluzione dell’esercizio 2
•
Osserviamo innanzitutto che le due resistenze centrali
sono in parallelo, conviene semplificare il circuito
sostituendole con la resistenza equivalente:
1
1 1 
Req      4W
 6 12 
•
Dopodiche’ notiamo che il circuito e` formato da due
maglie identiche. Questo significa che le correnti che
scorrono nelle maglie sono uguali e che bastera`
risolvere una sola delle due maglie.
A
3W
E1=2V
I1
3W
4W
I2
2V
E2=8V
2W
•
B
2W
Applichiamo la 2a legge di Kirchhoff alla maglia di
sinistra e imponiamo l’uguaglianza delle correnti:
E1  E2  I1 3  2  I1  I 2 4
I1  I 2
•
Otteniamo:
 6  13I
•
Quindi le correnti valgono:
I1  I 2  0.462 A
•
La ddp tra A e B e` uguale alla fem E2 meno la caduta
di potenziale sulla resistenza posta su AB (tenendo
conto che su AB scorre una corrente somma delle
correnti che circolano sulle due maglie):
VA  VB  E2  2  I  4  8  2   0.462 4  4.31A
Esercizio 3
Una bobina rettangolare di N=100 spire e dimensioni
a=2 m e b=1 m, ruota con velocita` angolare w=120p
rad/s attorno ad un asse mediano in un campo B
uniforme di 1 Tesla perpendicolare all’asse.
a)Trovare l’ampiezza della fem generata
Le estremita` dell’avvolgimento sono collegate,
tramite contatti striscianti, ad un carico puramente
resistivo R di 100 Ohm.
b) Trovare la potenza dissipata e
c) il momento meccanico necessario per generare
questa potenza
B
w
b
a
• Soluzione dell’esercizio 3
•
Per trovare la fem, consideriamo il flusso del campo
magnetico attraverso la bobina:
( B)  NBA cos 
q B
b
F
•
F
Dove A = ab e` l’area della spira e q  wt e` l’angolo
all’istante t. La fem e` data dalla legge di Faraday:
d ( B )
E
  NBAw sin wt
dt
•
L’ampiezza e` dunque:
E0  NBAw  100 1 2 1120p  7.54 10 4 V
•
•
La potenza dissipata nella resistenza e`:
2
2
E
E
P  i2R 
 0 sin 2 wt
R
R
Il cui valore medio nel tempo e`:

1 E02 1 7.54 104
P 

2 R 2
100

2
 2.84 107 W
•
Il momento meccanico e` dovuto alle forze agenti sui lati
‘a’:
M  Fb sin   NBai (t )b sin wt 
E0
 NBA sin 2 wt  M 0 sin 2 wt
R
•
La cui ampiezza e`:
E0 E02 2 P
2  2.84 107
M 0  NBA



 1.51105 Nm
R wR
w
120p
•
E il cui valor medio e`:
M  M 0 sin 2 wt 
1
M 0  7.55 10 4 Nm
2
Esercizio 4
Un’antenna e` accoppiata, tramite un’induttanza, ad un
circuito LC di sintonizzazione. L’induttanza L del circuito
vale 2 H, la capacita` C, variabile, dev’essere scelta in
modo da raccogliere onde di lunghezza d’onda di 1 km.
Trovare il valore di C.
L
C
• Soluzione dell’esercizio 4
•
Troviamo innanzitutto la frequenza dell’onda incidente:
3 108
5
 

3

10
Hz
3

10
c
•
La mutua induzione tra le induttanze dell’antenna e del
circuito indurra` una fem nel circuito. Questa fem genera
una corrente tanto maggiore quanto piu` la frequenza
naturale del circuito e` vicina a quella dell’onda. Si
trattera` dunque di scegliere opportunamente C in modo
tale da uguagliare queste due frequenze (o pulsazioni):
1
 2ponda
LC
wcircuito 
•
Da cui si determina il valore di C:
C

1
4p 
2

2
onda
1
4p 3 10
2
L

2
5 2
 1.4110 13 F