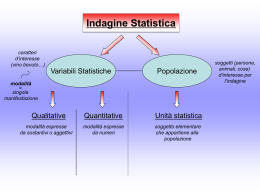
STATISTICA
descrittiva
Le origini della statistica e della
probabilità risalgono alla metà del
XVIII secolo, quando si iniziarono ad
affrontare con metodo scientifico le
osservazioni
relative
alle
caratteristiche demografiche delle
popolazioni umane e ai giochi
d‘azzardo.
Statistica e probabilità hanno un‘origine
piü recente delle tradizionali discipline
matematiche; Esse sono collegate alla
variabilità ed all‘incertezza dei fenomeni
della realtà e si propongono di introdurre
tecniche rigorose per prendere decisioni
razionali laddove la complessità o la
natura stessa delle situazioni sembrano
rendere
imprevedibile
e
caotico
il
susseguirsi degli eventi.
Con il progresso scientifico, sociale ed
economico emerse con forza l‘utilità di
acquisire sempre piu' numerosi dati
statistici sui quali i politici, gli economisti e
gli scienziati in genere potessero basare e
confrontare le loro decisioni e le loro
teorie. Il termine statistica deriva da
stato, infatti è nato per indicare la
scienza dello stato
Raccolta dati
La statistica
nasce dalla necessità di
conoscere l‘andamento di un certo
fenomeno per poter fare previsioni sulla
sua evoluzione o per prendere decisioni
riguardanti lo stesso fenomeno. Mediante
la raccolta di dati si ottengono
informazioni utili per elaborare
un
prospetto o un grafico che schematizza
e illustra in modo immediato lo stato del
fenomeno.
Le sue applicazioni
I settori dove la statistica trova maggiore
applicazione sono:
•La ricerca scientifica
•Le scienze demografiche e attuariali
•Le scienze economiche
•Le scienze sociali
•Le scienze per la programmazione economica
e territoriale
•La ricerca operativa
Definizioni
• Statistica: la scienza che ha come scopo lo
studio dei fenomeni collettivi
• Unità statistica: la minima unità di cui si
raccolgono i dati (singoli alunni)
• Popolazione (o universo): l‘insieme delle
u.s. (alunni della classe)
• Caratteri: sono le proprietà che sono oggetto
della rilevazione della popolazione (voto,
statura, ecc.)
Definizioni
• Modalità: sono i modi in cui si presenta il
carattere
I caratteri possono essere
•Qualitativi, indicati con espressioni verbali –sostantivi
o aggettivi(colore occhi)
•Quantitativi, esprimibili con numeri;Questi ultimi
possono essere:
• discreti (possono assumero solo determinati
valori, di solito interi, es: n° nati, produz. auto)
• continui (assumono qualsiasi valore all‘interno di
un dato intervallo, es: la temperatura, il prezzo di
un prodotto)
• Le Modalità dei caratteri qualitativi possono
essere ordinate o non ordinate.
Esempi:
• Modalità ordinate -L‘ordine di nascita dei
fratelli, il titolo di studio, il mese di nascita.
• Modalità non ordinate – la nazionalità, la
professione, il colore dei capelli
Tipi di statistica
L‘indagine statistica può seguire due procedimenti:
Nel caso di rilevazione totale si ha la statistica
descrittiva, che si occupa della raccolta, del
riordino, nonchè della presentazione e dell‘analisi
dei dati ottenuti dallo studio del fenomeno
collettivo;
• Nel caso di rilevazione campionaria si ha la
statistica inferenziale, che si occupa di
estendere i risultati ottenuti con la statistica
descrittiva ad insiemi più numerosi di quelli
studiati fornendo strumenti analitici per trarre
conclusioni e conseguenti decisioni.
Universo statistico
Si può distinguere in:
• Universo finito, cioò formato da un numero
limitato di unità statistiche (le rilevazioni possono
essere totali o campionarie)
• Universo infinito, cioè costituito da un numero
illimitato o molto grande di unità statistiche ( le
rilevazioni sono sempre campionarie)
Rilevazione dei dati
I dati possono essere raccolti mediante:
a) Intervista diretta alle unità statistiche;
b) Compilazione di un questionario:
c) Rilevazione per mezzo di esperimenti;
d) Utilizzo di dati già predisposti da enti che si
occupano di rilevazioni statistiche.
Esempio: il censimento si effettua con una
rilevazione totale mediante questionario. In
Italia l‘organo ufficiale che si occupa di
rilevazioni statistiche è l‘ISTAT attivo dal 1926.
Costruzione di un questionario
I questionari sono dei modelli di rilevazione
per acquisire dati statistici e sono costituiti
da un insieme di domande a risposta chiusa
o aperta; nel primo caso l‘intervistato deve
scegliere la risposta tra quelle indicate, nel
secondo caso può esprimersi liberamente.
Spoglio dei dati
Una volta raccolti i dati è necessario riordinarli e
sintetizzarli per poterne poi trarre qualche
conclusione. Per far questo per prima cosa si
effettua lo spoglio dei dati che consiste nel
leggere e classificare le risposte alle domande.
Dallo spoglio si ricavano le frequenze assolute
delle modalità.
Def: La frequenza assoluta è il valore associato a
una certa modalità di un carattere, cioè il n° di
unità statistiche corrispondenti a quella modalità.
Tabelle
Le tabelle che riportano le frequenze
assolute costituiscono una distribuzione
statistica e possono essere:
•Tabelle semplici;
•Tabelle composte;
•Tabelle a doppia entrata.
Tabelle semplici
Una tabella semplice si
presenta come un
prospetto a due
colonne: nella prima
sono riportate le
modalità, qualitative o
quantitative, nella
seconda l‘intensità
cioè la frequenza con la
quale la modalità si
presenta
Voto
Frequenza
4
2
5
1
6
4
7
8
2
9
1
10
Tabelle composte
Una tabella composta è a più colonne. Nella prima
colonna sono riportate le modalità di un carattere,
nelle altre le intensità riferite a casi diversi.
Voto alunni
classe
1-3
4-6
7-9
10
IVA Ginnasio
8
5
1
VA Ginnasio
10
6
1
IC scientifico
10
10
2
IIE scientifico
6
14
2
Tabelle a doppia entrata
Sono tabelle a più colonne, dove vengono raccolti i dati
relativi a 2 caratteri: nella prima colonna vi sono le
modalità del primo carattere, nella prima riga le modalità
del secondo carattere.
Colore
capelli
biondi
neri
verdi
1
2
azzurri
4
2
rossi
castani
Colore occhi
1
1
1
castani
2
5
neri
5
4
Rappresentazioni grafiche
Non aggiungono nuove informazioni,
ma consentono una visione
immediata e complessiva del
fenomeno considerato.
Diagrammi a coordinate cartesiane
Grafici a nastri o a colonne
Istogrammi
Diagrammi a torta
Diagrammi in coordinate cartesiane
Sono significativi quando una
grandezza è funzione dell‘altra, ed
entrambe variano con continuità.
Spesso la variabile indipendente è
costituita dal tempo, in funzione del
quale si studia l‘andamento dell‘altra
grandezza.
Grafici a nastri o a colonne
Sono rappresentazioni grafiche molto
usate per modalità qualitative dove
vengono disegnate per ogni modalità
del fenomeno studiato, rettangoli di
uguale larghezza e di lunghezza
proporzionale alle frequenze delle
modalità.
Istogrammi
Sono utilizzati prevalentemente per
rappresentare fenomeni aventi
modalità quantitative espresse con
intervalli di valori. Sono costituite da
rettangoli aventi come base
l‘ampiezza dell‘intervallo e come
altezza la frequenza.
16
14
12
10
Alti
Bassi
8
6
4
2
0
Altezza
Diagrammi a torta
Sono significativi per rappresentare
come una popolazione viene
suddivisa, rispetto ad un determinato
carattere
L‘ampiezza x dei settori si calcola
risolvendo la proporzione seguente:
x:360°=f:T
ove
f=frequenza
T=totale della popolazione
Altezza
16;
80%
Alti
Bassi
4;
20%
Media
La media è un numero che ne
sintetizza molti e consente di averne
una visione unitaria.
la media è un valore
opportunamente scelto e
compreso tra il minimo e
il massimo dei dati.
Medie mobili o ferme
Moda e mediana sono medie mobili, cioè
sono quelle medie per la cui
determinazione non si usano tutti i dati.
media aritmetica,
quadratica,
geometrica, armonica
sono medie ferme, per il cui calcolo si
conteggiano tutti i dati disponibili
Moda
Si dice moda il carattere o il valore cui
corrisponde la massima frequenza.
La serie dei numeri 5,6,8,8,8,12,12,14
ha moda 8
La serie 5,6,8,8,8,12,12,14,14,14
ha due mode: 8 e 14
Mediana
Si dice mediana il valore che occupa il posto
di mezzo, quando i dati sono disposti in
ordine crescente.
La serie dei numeri 5,6,8,8,8,12,12,14
ha mediana (8+8)/2
La serie 5,6,8,8,8,12,12,14,14
ha mediana 8
Medie mobili o ferme
Contrariamente alle medie ferme, la
Mediana e moda possono essere
determinate anche quando i dati non
hanno carattere numerico:
suff, buono, buono
Medie mobili o ferme
Può accadere che cambiando alcuni dei
dati, anche in modo vistoso, moda e
mediana non cambino; ciò fa perdere
di significato alle grandezze.
Ecco perchè si introducono le
medie ferme