1
COS’E' L'ELETTROTECNICA?
E' la tecnica dell'energia elettrica, cioè le possibili applicazioni
degli effetti prodotti dalle cariche, ferme o in movimento.
L'ELETTROMAGNETISMO E' ALLA BASE DI UNA
GRANDE QUANTITA' DI FENOMENI FISICI
•
•
•
•
•
•
•
•
conversione elettromeccanica dell'energia
comunicazione in fibra ottica
dispositivi a micro-onde
ricezione televisiva
comunicazione via satellite
radar
oscilloscopi
etc…
2
DAI CAMPI…
B
E  
t
D
H  J 
t
  D   lib
B  0
Fisica
Leggi di
Maxwell
Elettrotecnica
Applicazioni
Fenomeni
…AI CIRCUITI
3
CAMPO
X1 f(X1)
X2 f(X2)
X3 f(X3)
X4 f(X4)
In una regione dello spazio diciamo che è presente un campo se in tale
regione è definita una grandezza fisica funzione della posizione.
4
Esempio: Campo di Temperature
CAMPO VETTORIALE
X1 f(X1)
X2 f(X2)
X3 f(X3)
X4 f(X4)
Se la grandezza fisica che definisce il campo è vettoriale, il campo
è detto vettoriale.
5
Esempio: Campo di Velocità
CAMPO DI FORZE
X1 E(X1)
X2 E(X2)
X3 E(X3)
X4 E(X4)
Se la grandezza fisica che definisce il campo è una forza, il campo
è detto Campo di Forze.
6
Esempio: Campo Elettrico
Campo Elettrico
F
Qq 
F  k 2 r Legge di Coulomb
r
q
+
F
Q
E   k 2 r Campo Elettrico
q
r
Q
dL  E  dl Lavoro Elementare
B
 E  dl  V B   V  A
A
A
D
dA
B
Differenza di potenziale
+ Q
Q   D  dA
D = Densità di Flusso Elettrico
7
Campo Magnetico
F  I  B
i
forza indotta
pollice (pesoforza)
indice (i corrente)
B
mano destra
medio (m campo magnetico)
H
I
I
2 r
U m   H  dl  I
Legge di Biot-Savart
Legge di Ampére
8
RELAZIONI COSTITUTIVE DEL MEZZO
eo è la costante di proporzionalità fra la densità di flusso elettrico
D e l'intensità di campo elettrico E nel vuoto:
D  e0  E
m0 è la costante di proporzionalità fra la densità di flusso magnetico
B e l'intensità di campo magnetico H nel vuoto
H
costanti universali
1
m0
B
simbolo
valore
unità
velocità della luce nel vuoto
c
3  108
m/s
permeabilità del vuoto
m0
4  10-7
H/m
permettività del vuoto
e0
1
 10 9
36
F/m
9
Ipotesi di Quasi-Stazionarietà I
B
B
 0  E  
0
t
t
 E  0
L
 E  dl  0
L
Campo
E
IRROTAZIONALE
10
Legge di Kirchhoff sulle Tensioni
P2
E  dl  Lavoro di E per portare una carica unitaria
Da P1 a P2  Differenza di Potenziale V(P1) – V(P2)
dl
 E  dl  0
P1
L
[V(P2)-V(P1)]+[V(P3)-V(P2)]+[V(P4)-V(P3)]+[V(P5)-V(P4)]+[V(P6)-V(P5)]+[V(P6)-V(P1)]=0
P2
P3
P4
P1
P6
P5
La somma delle differenze di potenziale
calcolati lungo un qualunque percorso
chiuso è pari a
zero
11
Ipotesi di Quasi-Stazionarietà II
D
D
 0  H  J 
J
t
t
 H  J
L
Circuitazione del Campo H su L
H

dl

I

L
pari alla corrente concatenata
12
Legge di Kirchhoff sulle Correnti
 H  dl  I
I
L
S2
L
S1
I
L’integrale lungo L è pari alla corrente che
attraversa qualunque superficie che ha L
come bordo, perciò la corrente che
attraversa S1 è uguale alla corrente che
attraversa S2
Dunque:
La somma delle correnti che attraversano
una qualunque superficie chiusa è pari a
zero
13
Grandezze Descrittive
Q
V
Intensità di Corrente:
Quantità di carica che attraversa
la sezione del conduttore nell’unità
di tempo
I
I
dQ
dt
A
Ampere-metro
Differenza di Potenziale:
Lavoro che il campo elettrico compie
nel portare una carica unitaria da un
nodo del circuito ad un altro
I
V
Volt-metro
14
Ipotesi della TEORIA DEI CIRCUITI
Le lunghezze d’onda sono molto maggiori
delle dimensioni del circuito
PARAMETRI CONCENTRATI
15
Parametri Concentrati
Hp: Le dimensioni del circuito sono
trascurabili rispetto alla
lunghezza d’onda delle
tensioni e delle correnti
l
Non ci sono fenomeni di
propagazione
Non compaiono derivate spaziali
Casi in cui l’ipotesi non è ammissibile:
•Microprocessori
•Antenne
•Linee di Trasmissione
16
ESEMPI
1)
CIRCUITO AUDIO
•frequenza più alta ~25 kHz
•corrispondente l = 12 km (c/f )
SUPERIORE DI GRAN LUNGA ALLE DIMENSIONI
DI UN CIRCUITO DEL GENERE
2)
CIRCUITO DI UN CALCOLATORE
• f può essere 500 MHz
• corrispondente l = 0,6 m
IL MODELLO A PARAMETRI CONCENTRATI PUO'
NON ESSERE SUFFICIENTEMENTE ACCURATO
3)
CIRCUITO A MICRO ONDE
• l varia tra 10 cm e 1 mm
LE LEGGI DI KIRCHHOFF NON VALGONO
17
SISTEMA INTERNAZIONALE
Definizioni:
metro: la definizione deriva da quella
QUANTITA'
UNITA'
SIMBOLO del secondo e dalla velocità della luce
nel vuoto.
Lunghezza
metro
m
c = 299 792 450 m/s
secondo: 9 192 631 770 periodi della
Massa
kilogrammo
kg
radiaizone emessa da una particolare
Tempo
secondo
s
transizione di un atomo di cesio
kilogrammo: massa di un provino di
Intensità di
Ampére
A
platino-iridio conservato al International
Corrente
Bereau of Weights and Measurements di
Sevres
Costanti Universali
Ampére: la corrente costante che, se
c velocità delle onde elettromagnetiche nel
mantenuta in due conduttori rettilinei
8
vuoto  3 × 10 m/s
paralleli di lunghezza infinita e di
-7
m0 permeabilità del vuoto 4 × 10 H/m
sezione circolare trascurabile, messi ad 1
-12
e0 permettività del vuoto 8,854 × 10 F/m metro di distanza, nel vuoto, producono
fra i due conduttori una forza pari18a
2 × 10-7 N/m
EQUAZIONI DIMENSIONALI
Es:
• CARICA ELETTRICA
I
dq
dt

q [C]
C  A s
• INTENSITA' DI CAMPO ELETTRICO
poiché
E
F
q

da cui si ricava anche
E [V/m]
V kg  m kg  m


m s2  A  s A  s3
V
kg  m
A  s2
• INDUZIONE MAGNETICA B [T]
poiché
 V  s kg  m 2  s
kg
B  2 

S m
A  s3  m2 A  s2
   e  dt  V  s
19
GRANDEZZE ELETTRICHE
GRANDEZZA
SIMBOLO
UNITA' DI MISURA
SIMBOLO
AMMETTENZA
Y
Siemens
S
CAMPO ELETTRICO
E
Volt/metro
V/m
CAMPO MAGNETICO
H
Ampére/metro
A/m
CAPACITA' ELETTRICA
C
Farad
F
CONDUCIBILITA'
g
Siemens/metro
S/m
Q,q
Coulomb
C
G
Siemens
S
I,i
Ampére
A
J
Ampére/metro quadro
A/m2
d,
Coulomb/metro cubo
C/m3
ENERGIA
W
Joule
J
FLUSSO MAGNETICO

Weber
Wb
FORZA
F
Newton
N
FORZA ELETTROMOTRICE
e,E
Volt
V
FORZA MAGNETOMOTRICE
Fmm
Ampére-spire
A , As
FREQUENZA
f
Hertz
Hz
IMPEDENZA
Z
Ohm
W
INDUTTANZA
L
Henry
H
INDUZIONE MAGNETICA
B
Tesla
T
MUTUA INDUTTANZA
M
Henry
H
PERMEABILITA' MAGNETICA
m
Henry/metro
H/m
PERMEANZA
P
Weber/Ampére
Wb/A
20
PERMETTIVITA' ELETTRICA
e
Farad/metro
F/m
CARICA
CONDUTTANZA
CORRENTE
DENSITA' DI CORRENTE
DENSITA' VOLUMICA DI CARICA
GRANDEZZA
SIMBOLO
UNITA' DI MISURA
SIMBOLO
POLARIZZAZIONE ELETTRICA
Pe
Coulomb/metro quadrato
C/m2
POLARIZZAZIONE MAGNETICA
Pm
Tesla
T
POTENZA ATTIVA
P
Watt
W
POTENZA REATTIVA
Q
VoltAmpére reattivi
VAR
POTENZA APPARENTE
S
Volt Ampére
VA
V,v
Volt
V
POTENZIALE VETTORE
A
Weber/metro
Wb/m
REATTANZA
X
Ohm
W
RESISTENZA
R
Ohm
W
RESISTIVITA'
s
Ohm metro
Wm
RD
Volt/metro
V/m
SPOSTAMENTO ELETTRICO
(DENSITA' DI FLUSSO ELETTRICO)
D
Coulomb/metro quadrato
C/m2
SUSCETTANZA
B
Siemens
S
TEMPO
t
secondo
s
V,v
Volt
V
POTENZIALE ELETTRICO
RIGIDITA' DIELETTRICA
TENSIONE
21
CIRCUITO ELETTRICO
E' un insieme di componenti elettrici connessi tra loro mediante
conduttori perfetti
Circuito Elettrico di soli Bipoli
22
COMPONENTI
terminale
BIPOLO
R
L
E
C
A
superficie limite
morsetto
MONOPOLO
M
TRIPOLO
Transistor
Motore
Trifase
Non vengono inclusi fra i
componenti nello studio
della Teoria dei Circuiti
COLLEGAMENTO
Due o più componenti si dicono collegati se
hanno uno o più morsetti in comune
23
STRUMENTI DI MISURA
CORRENTE
TENSIONE
v = v( t )
v = vAB = -v’ = -vBA
A
i
i = i( t )
i = -i’
i’
v’
v
B
UNITA’ DI MISURA:
Volt (V)
UNITA’ DI MISURA:
Ampére (A)
STRUMENTO DI MISURA: Ampéremetro STRUMENTO DI MISURA: Voltmetro
inserzione
Vi
i
A
inserzione
i
Vi piccolissima  ideale ri = 0
V
iv
A
B
VAB
iv piccolissima  ideale rv = 
24
3
2
i2
v2
1
CONVENZIONI
{i1 , i2 , … , in } Indipendente
{v1 , v2 , … , vn } Completo
i3
in
i1
v1
n
vn
VARIABILI DESCRITTIVE
0
1
i
v
1
i1 i2
v1
0
1
v
1
convenzione degli utilizzatori
0
0
i
1
2
v2
i1 i2
v1
0
2
2
1
2
convenzione dei generatori
v2
0
0
25
1
i  v  G v
R
v  R i
RESISTORE i
v
per un conduttore di lunghezza l e sezione A:
alluminio
tungsteno
silicio
100
1,63  108
MARRON
1
101
1,72  108
ROSSO
2
102
2,44  108
ARANCIO
3
103
4
104
5
105
6
106
7
107
8
108
2,83  108
6,52  108
2 300
GIALLO
VERDE
BLU
VIOLA
GRIGIO
BIANCO
9
-
ORO
10-1
ARGENTO
10-2
NERO o null
TOLL.ZA
oro
0
 W  m)
MULTIPLO
rame
CIFRA
argento
COLORE
MATERIALE
NERO
-
±5%
±10%
±20%
l 1 l
R   
A g A
prefisso
simbolo
significato
atto
a
10-18
femto
f
10-15
pico
p
10-12
nano
n
10-9
micro
m
10-6
milli
m
10-3
centi
c
10-2
deci
d
10-1
deca
da
101
etto
h
102
kilo
k
103
mega
M
106
giga
G
109
tera
T
1012
exa
E
1015
peta
P
1018
26
CAPACITORE
q  C v
i+
d
+
+
+ + + ++
v
+ + ++
dq
dv
+
- C
- dt
dt
i
- dq
i
dt
er
MATERIALE
neoprene
6,46
silicone
3,20
mica
5,40 - 9,0
carta
2,99
acqua distillata
78,20
aria
1
A
ce
d
dv
i C
dt
e  e0 er
27
INDUTTORE
INDUTTORE
i
i
  Li
d
v
dt
di
v  L
dt
28
GENERATORI IDEALI
Generatore ideale di tensione
v(t)
i(t)
e(t)
v(t) = e(t)
Corto Circuito
Generatore ideale di corrente
v(t)
i(t) = a(t)
Circuito Aperto
i(t)
v(t)
i(t)
a(t)
i(t)
v(t) = 0
Caso degenere del generatore
di tensione o del resistore di
resistenza nulla
v(t)
i(t) = 0
Caso degenere del generatore
di corrente o del resistore di
resistenza infinita o
conduttanza nulla
29
GENERATORI PILOTATI
v1
v=b v1
b : parametro di controllo a-dimensionale
i1
v=R i1
R : parametro di controllo
dimensionalmente è una resistenza
v1
i=g v1
g : parametro di controllo
dimensionalmente è una conduttanza
i1
esempio:
ag
R2
i1
R1
0,5 i1
I generatori dipendenti o pilotati sono
componenti essenziali nei circuiti
amplificatori, in cui l'ampiezza
dell'uscita è maggiore di quella
dell'ingresso.
Inoltre servono ad isolare una
porzione di circuito o a fornire una
resistenza negativa
i=a i1
a : parametro di controllo a-dimensionale
30
TRASFORMATORE IDEALE
v1  n  v2

base di definizione mista:
v1
v2

1
[ v1 ; i2] o [v2 ; i1]
i



i
2
 1
n
v1
pt   v1i1  v2i2  v1i1   n  i1   0
n
i1
n
i2
Il trasformatore ideale è trasparente alle potenze
E' un componente PASSIVO non dissipativo
Non è dotato di stato
31
MUTUA

I1
N1
i1 M i2
v1 L1
L2 v2
 d1
I2
d 2
N2
di1
di2

 v1  L1 dt  M dt

di1
di2
v2  M
 L2
dt
dt

32
AMPLIFICATORE OPERAZIONALE
L’Amplificatore Operazionale (Operational Amplifier - OP) è un
dipositivo elettronico che si comporta come un generatore di
tensione controllato in tensione
CONFIGURAZIONE DEI PIN
SIMBOLO CIRCUITALE
+
V
7
BILANCIAMENTO
ING. INVERTENTE
ING. NON INVERT.
V-
1
2
3
4
8
7
6
5
i _
vd
i
+
2 
SCOLLEGATO
ING. INVERTENTE
V+
3 
USCITA
ING.
NON
INVERT.
BILANCIAMENTO
vd  0
i  i  0
 
4 -1
V
6
USCITA
5
AZZERAMENTO
OFFSET
LE ALIMENTAZIONI VENGONO SPESSO OMESSE NEGLI SCHEMI
CIRCUITALI, MA L’OP DEVE SEMPRE ESSERE ALIMENTATO
33
MODELLO CIRCUITALE
v1
vd
v2
Ri
A·vd
Ro
Generatore di tensione
controllato in tensione
vo
vd  v2 v1
vo  A  vd  A  v2 v1 
A: guadagno di tensione ad anello aperto
valori tipici
A
105108
Ri
1061013 W
Ro
10100 W
Vcc
5 24 V tensione di
alimentazione
vo
Vcc
saturazione positiva
vd
saturazione negativa
-Vcc
34
AMPLIFICATORE OPERAZIONALE IDEALE
i1 = 0
v1 i2 = 0
_
i1  0
i2  0
vd
+
vo
v2 = v1
A

 Ri   
vd  v2  v1  0
R  0
 o
v2  v1
NELLA MAGGIOR PARTE DELLE APPLICAZIONI SI CONSIDERANO OP
IDEALI NELLA REGIONE LINEARE DI FUNZIONAMENTO
NULLORE
i
i0
v0
0

v
v0  0



 i0  0
v qualsiasi



 i qualsiasi
35
AMPLIFICATORI ADINAMICI -TABELLA RIASSUNTIVA
inseguitore
di tensione
vo  vs
amplificatore
invertente
vo  
R2
R2
 vs
R1
amplificatore
non invertente
 R 
vo  1  2   vs
 R1 
R2
R1
vs
vs
RL
vo
amplificatore
sommatore
vo
v
v 
v
vo   Ro  1  2  3 
 R1 R2 R3 
RL
R1
vs
amplificatore
differenziale
vo
vo 
RL
R2
 v1  v2 
R1
R3
R2
v3
Ro
R1
v2
v1
R2
R1
vo
RL
v2
R1
v1 R2
vo
RL
36
BASE DI DEFINIZIONE
UN COMPONENTE SI DICE DEFINITO SU BASE TENSIONE SE, IMPONENDO
LE TENSIONI, LE CORRENTI SONO NOTE UNIVOCAMENTE ATTRAVERSO LE
CARATTERISTICHE O LE EQUAZIONI DEL COMPONENTE.
VICEVERSA, E' DEFINITO SU BASE CORRENTE SE, IMPONENDO LE
CORRENTI, SI TROVANO UNIVOCAMENTE LE TENSIONI.
Esempi:
i
i
e R
v0
e
R
base corrente
i
e
i
i
a R
base tensione
base corrente
i
v  Ri  R a
i
i
i
a
v
v
v
v
assurdi fisici
DIODO
entrambe le basi
DIODO TUNNEL
base tensione
37
i1 1
2 i2
v1
v2
0
i1
1
2
R1 R2
v1
i2
e1
a) base corrente
a1
v1,i2 
R2  0 ; 
BASE TENSIONE, CORRENTE E MISTA
i1
i2
R1
v1
R2
e2
v2
i1
fissati:
i2
R1
v1
BASE MISTA
R1  0 ; 
v2
0
a) base tensione
ESEMPI:
 i1  0


v2  0
R2
v2
a2 fissati:
v1 e1

i

 1 R  R
1
1

v
e
i2  2  2

R2 R2
 v1  e1


v2  e2
trovati:
 i1  a1


i2  a2
 v1  R1  i1  R1  a1

trovati:
v2  R2  i2  R2  a2
38
I Principio di Kirchhoff
I2
I3
I4
I1
I5
I7
I6
I1+ I2+ I3+ I4+ I5+ I6+ I7=0
39
II Principio di Kirchhoff
V2
V3
V4
V1
V10
V9
V8
V5
V6
V7
V1+ V2+ V3+ V4+ V5+ V6+ V7 + V8 + V9 + V10 = 0
40
ESEMPI:
i
5A
a)
5 + i - (-3) - 2 = 0
2A
-3 A
i = -6 A
v
b
b)
c
15 V
10 V
v=3V
a
d
2V
c)
-15 + v +10 + 2 = 0
4A
i2
4A
3A
i1
2A
8A
i
trovare i
4 - 3 - i1 = 0  i1 = 1 A
1 + 4 + 2 - i2 = 0  i2 = 7 A
7 - 8 - i = 0  i = -1 A
4 + 4 - 8 - i + 2 - 3 = 0  i = -1 A
41
TEORIA DEI GRAFI
Circuito
Grafo
Tensioni
Correnti
42
Albero & Co-Albero
Co-Albero:
Complemento dell’
Albero nel Grafo
Albero:
1) Grafo Connesso
2) Comprende tutti i nodi
3) Non comprende percorsi chiusi
43
Equazioni Topologiche
b
a
d
l
e
z
h
m
n
o
e
c
a b
l
p
g
d
f g
i
q
q
r
k
x
n
s
n-1 co-cicli
a
h
i
z w
m
a
t
v
u
d
l
b
z
n
m
h
m
l
o
p
d
e
b c
e
g
i
q
z w
h
i
x
k
v
n
r
q
f g
s
u
t
l-n+1 maglie
44
Esempio
v2
v1
E
i
g
R1 i 1
v vL
a
i L R2 i 2 i C
C
L v
C
a
b
b
c
Albero a stella
g
vg  E
v1  R1  i1
v2  R2  i2
diL
vL  L
dt
dvC
iC  C
dt
4 nodi
5 lati
ia  ia  0

ib  ia  ib  0
ic  ib  0

ig  i1  0

 iL  i1  i2  0
 iC  i2  0
va  vb  va  0
v  v  v  0
c
b
 b
v1  vL  vg  0

v2  vC  vL  0
10 incognite
5 eq Componenti
3 eq LKC
2 eq LKT
45
Teorema di Tellegen
Dato un grafo:
a
v4
E
R1
v1 v2
a
Siano:
{ik} un sistema di correnti compatibile
{vk} un sistema di tensioni compatibile
b
b
c
Risulta:
v5
R2
L v3
v i
k k
0
k
Stesso grafo
4
5
C
Circuiti differenti
i5
i4
i3
L2
i1 L1
R
A
C
i2
1
2
3
Sk vk ik = 0
Caso particolare:
Se si considerano tensioni e correnti dello
stesso circuito otteniamo la
46
Conservazione delle Potenze
PROPRIETA' ENERGETICHE
• Potenza Assorbita da un Bipolo: p(t) = v(t) · i(t) (convenzione
normale) è la potenza che entra nella superficie limite del bipolo.
Con la convenzione normale si parla di potenza assorbita.
Unità di misura Watt [W]
• Energia Elettrica assorbita in un intervallo dt: dw  v(t) · i(t) · d
a) dw  0 d t 
elemento puramente dissipativo
L  i2
b) 0  dw  0  energia accumulata in bipoli di tipo L e C: E  2
C  v2
E
2
c) 0  dw  0  elementi di capacità infinita, come i generatori ideali,
I COMPONENTI ELEMENTARI SONO TALI PERCHE'
INVESTONO IN UN SOLO TIPO DI ENERGIA
47
VERIFICA DELLA PASSIVITA'
t n1
vi ii

i 1
 p  d   
t

RESISTORE
i
v R
E
p  v  i  R  i2
E
E2
i  p
R
R
 d  0
t
La funzione integranda è sempre  0
 p   d  
t

t

E2
 d  0
R
CONDENSATORE
v
i
dv
dt
d 1

v  et   p   Cv 2 
dt  2

p  v i  v C
C
t


t 1

p   d    Cv 2 d  0
2

per t = - il condensatore è scarico
analogamente per l'INDUTTORE
t2
p
t1
Sono componenti che hanno lo STATO ZERO W  
t
1
, t2 
 d  0
48
Reti in Regime Stazionario
49
COMPONENTI ELEMENTARI IN REGIME STAZIONARIO
Per circuiti assolutamente stabili, in presenza di eccitazioni costanti
nel tempo:
•Generatore indipendente di tensione
•Generatore indipendente di corrente
i
i
v
E
•Resistore
v  E  cost
v
•Induttore
i
v
R
v  R i 
V  RI
A
i  A  cost
•Condensatore
i
v
L
di
0
dt
V  0 (cto  cto)
v  L
i
v
C
dv
0
dt
50
I  0 (circuito aperto)
i C
Esempio:
I3
E1
V1
I2
I1 R
I
4
1
V3 V4
R5
R4 I5
I6
V5
V7
I7 R
I8
3
V1  R1I1
V2  R2 I 2
V3  E1
V4  R5 I 4
V5  R4 I 5
V6  R6 I 6
V7  R3 I 7
V8  E2
f
R2
a
V2
R6
V6
V8
E2
ia  i f  0
ib  ih  i f  0
ic  ig  i f  0
 id  ig  ih  0
ie  ih  0
v f  va  vb  vc  0
vg  vc  vd  0
vh  vb  vd  ve  0
c
g
b
d
h
e
I 3  I1  0
I 5  I 7  I1  0
I 5  I 2  I1  0
I6  I2  I7  0
I8  I 7  0
V1  V3  V5  V4  0
V2  V4  V6  0
V7  V5  V6  V8  0
51
…continua
 R1 0
 0  R2
 0
0

0
 0
0
 0
 0
0
 0
0

0
 0
 1 0
 1 0
 1
1

1
 0
0
 0
 0
0
 0
0

0
 0
0 0
0
0
0
0 0
0
0
0
0 0
0
0
0
0  R5 0
0
0
0 0  R4 0
0
0 0
0  R6 0
0 0
0
0  R3
0 0
0
0
0
1 0
0
0
0
0 0
1
0
1
0 0
1
0
0
0 0
0
1
1
0 0
0
0
1
0 0
0
0
0
0 0
0
0
0
0 0
0
0
0
A x  b
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
1
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
A A x  I  x  x  A b
0  I1   0 
0  I 2   0 
0  I 3   E1 
    
0  I 4   0 
0  I 5   0 
0  I 6   0 
0  I 7   0 
    
1   I 8   E2 


0 V1   0 
0 V2   0 
0 V3   0 
    
0 V4   0 
0 V5   0 
0 V6   0 
0 V7   0 
    
1 V8   0 
52
RESISTORI IN SERIE
V1
V2
A
I
R1 I1 I2 R2 I2
Vn
Vi
VAB
Ri
In-1 In
Rn
B A
I
VAB
B
Req
I1  I 2    I i    I n  I
VAB  V1  V2    Vi    Vn  R1I1  R2 I 2    Rn I n 
R1    Rn   I  Req  I 
Req   Ri
i
53
PARALLELO DI RESISTORI
A
A I A
A
I1
R1
B
Vi  Ri I i I i 
V1
I2
R2
V2
Ii
Vi
Ri
B
B
B
A
Vi
 GiVi
Ri
V1  V2    Vi  Vn  V
In
Vn
Rn
B
V1
Vn
I  I1    I n 


R1
Rn
1
1 
       V
Rn 
 R1
1
1
Geq   Gi   
Req
i
i Ri
54
PARTITORE DI TENSIONE
I
R1
Ri
R2
V
Rn
Vi
V  R1    Rn  I  I  V
Vi  Ri I
R
h
h
Ri
Vi  V 
 Rh
h
I
Nel caso di due soli resistori:
V1
V
V2
R1

V

V

 1
R1  R2


V  V  R2
R2  2
R1  R2
R1
55
PARTITORE DI CORRENTE
I
V
I1
I2
I3
In
R1
R2
Ri
Rn
V
Ii 
 V  Gi
Ri
I  I1  I 2    I n 
V  G1  G2    Gn   V 
I
 Gh
h
Gi
 I i  Gi  V 
I
 Gh
h
I
Nel caso di due soli resistori:
R1
I1 R2
R2

I

I

1
R1  R2

I2 
 I  I  R1
 2
R1  R2
56
Esempi:
3 kW
2 kW
3/2 kW
Oppure: Vx 
2 kW
24 V
5/2 kW
1,5 kW
Oppure:
Vx=?
I
I
4 kW
24 V
Vx=?
24 V
I=2,4 mA
Vx =9,6 V
4kΩ
4
 24 V   24 V  9,6 V
2  3  1  4kΩ
10
Ix=?
5 kW
10 kW
1 kW
2 kW
3 kW
4 kW
24 V
3 kW
5/7 kW
6 mA
24 V
2 kW
0,5 kW
3V
Ix =3 V / (5/7 kW = 4,1 mA
1,5 kW
7
7
mS
5
Ix 
 6 mA  5  6 mA  4,1 mA
2
2 1 7
   mS
5 5 5
57
TRASFORMAZIONE STELLA-TRIANGOLO
A
A
RA
RC
C

RAB RCA
R

 A
R0

RBC RAB

R

 B
R0

RCA RBC

R

 C
R0

0
RCA
RAB
RB
B
R0  RAB  RBC  RCA
C
 RAB  RA  RB  G0

RBC  RB  RC  G0
R  R  R G
C
A
0
 CA
Nel caso di tre resistenze uguali sarà:
B
RBC
G0 
R
RY 
3
1
1
1


RA RB RC
58
Esempio:
0,25 kW 0,625 kW
1 kW
A
2A
2 kW
C
4 kW
Ix 
5 kW
B
Ix=?
1 kW
1
1,625
1
1

5,25 1,625
A
2A
C
4 kW
0,25 kW
1,25 kW
B
1 kW
Ix=?
A
2A
5,25 kW
Ix=?
1,625 kW
 2 A  1,527 A
59
TEOREMI DI THEVENIN E NORTON
In una rete lineare, comunque complessa, contenente bipoli lineari,
le tensioni e le correnti in ciascun lato possono essere determinate
sommando i contributi dovuti ai singoli generatori presenti, agenti
uno alla volta.
A I
(Passivazione dei generatori)
V
TEOREMA DI THEVENIN
A I
Req
Eeq
V
B
V  Eeq  Req I
TEOREMA DI NORTON
A I
Aeq Geq
V
B
I  Aeq  GeqV
60
Thevenin
& Norton
AN
ETh
ETh = tensione a vuoto
AN = corrente in c.to c.to
GN
RTh
RTh = resistenza circuito passivato
GN = conduttanza circuito passivato
A I
A I
RTh
ETh
V
B
V  ETh  RTh I
AN
GN
V
B
I  AN  GNV
61
Esempio:
2 kW
5 kW
12 V
Nel resistore R circola una corrente di
2 mA. Quanto vale R?
I=2 mA
5 kW
R=?
1,5 kW
2 kW
2 kW
12 V
5 kW
5 kW
Eth=?
12 V
2,5 kW
Eth=?
ETh 
2,5 kW
 12 V  5 V
2  2,5  1,5kW
1,5 kW
1,5 kW
2 kW
5 kW
5 kW
Rth=?
3,5 kW
2,5 kW
Rth=?
1,458 kW
Rth
1,5 kW
1,458 kW
5V
I=2 mA
R=?
5 V  1,458 Ω  2 mA  R  2 mA
5 V  1,458 kΩ  2mA
R
 2,084 kΩ
2 mA
62
METODO DELLE CORRENTI DI MAGLIA
E2
R
R
E1
1
J1
I1 E4
R4
I4
2
I5
R5
J2
R6 I6
I1  J 1
I2
I 5  J1  J 2
I3
I6  J 2  J3
E3
E1  E4  R1 J1  R5 J1  J 2   R4 J1  J 3 

 E2  R2 J 2  R6 J 2  J 3   R5 J1  J 2 
E  E  R J  R J  J   R J  J 
4
3 3
4
1
3
6
2
3
 3
 R11
 

 RM 1
R12
RM 2
R1M   J1   E1 
      
   
 RMM   J M   EM 

I3  J3
I1  J 1  J 3
J3
R3
I2  J2
Le equazioni ai nodi
sono identità
E1  E4  R1 I1  R5 I 5  R4 I 4

 E2  R2 I 2  R6 I 6  R5 I 5
E  E  R I  R I  R I
4
3 3
4 4
6 6
 3
E1  E4  R1  R5  R4 J1  R5 J 2  R4 J 3

 E2   R5 J1  R2  R5  R6 J 2  R6 J 3
E  E   R J  R J  R  R  R J
4
4 1
6 2
3
4
6
3
 3
Rii : auto-resistenza
della maglia i
Rij : mutua resistenza
tra la maglia i-esima e
la maglia j-esima
 E1   EV 1   EI 1 
       
  
 

 EM   EVM   EIM 
63
METODO DEI POTENZIALI NODALI
1
VR 4
VR 3
2
R4
V1
A1
R5
V2
3
VR 2
R2
R3
V3
4
A2
V4
R1
VR4  V1  V2
VR3  V2  V3
VR2  V3  V4
Le equazioni alle maglie
sono identità
G11 G12  G1n  V1   A1  n = N -1
 
      

     Gii : conduttanza propria del
Gn1 Gn 2  Gnn  Vn   An 
nodo i
Gij : conduttanza mutua tra i
nodi i e j
 A1   AI 1   AV 1 
      
     
 An   AIn   AVn 
Noti i potenziali si può risalire a tutte le incognite
64
TEOREMA DI MILLMANN
A
R1
E1
R2
E2
Ri
R3
E3
Ei
Rn
E1G1
G1
EnGn
Gn
En
B
A
G
i
i
E G
i
i
B
G E

G
i
i
VAB
i
i
i
i
65
TEOREMA DEL MASSIMO TRASFERIMENTO DI POTENZA
a
THEVENIN
RTH
ETH
RL
b
i
RL
p
b
 ETH
p  RL i 2  RL  
 RTH  RL
a
pmax



2
RTH
RL
SI HA LA MASSIMA POTENZA TRASFERITA AL CARICO QUANDO LA
RESISTENZA DEL CARICO E’ UGUALE ALLA RESISTENZA DI
THEVENIN VISTA DAL CARICO:
RL = RTH
Dimostrazione:
 RTH  RL 2  2 RL RTH
dp
2
 VTH 
4
dRL


R

R
TH
L

 RL 
  0  RTH  RL  2 RL  0  RL  RTH


p max
VTH2

4 RTH
66
Reti in Regime Sinusoidale
67
IN UNA RETE ASSOLUTAMENTE STABILE, IL REGIME SINUSOIDALE
VIENE CONSEGUITO DA TUTTE LE VARIABILI DELLA RETE
METODO SIMBOLICO
U , A sono due fasori
m
A
y
j
U
verso positivo
per le fasi
(convenzionalmente)
U  U  e jj
H  H  e jy
A  H U  e j j y 
e
Le grandezze sono iso-frequenziali, quindi, dopo un certo tempo, l'istante iniziale
perde significato ed è superfluo indicare il riferimento degli assi. L'importante è
che le diverse grandezze fasoriali stiano in un determinato rapporto di fase tra loro
ANTICIPO  ANGOLO POSITIVO
RITARDO  ANGOLO NEGATIVO
Nella figura, A è in anticipo rispetto a V
CASI PARTICOLARI:
a) y =  / 2 i fasori sono in quadratura
b) y = 
i fasori sono in opposizione di fase
c) y = 0
i fasori sono in fase
PRINCIPI DI KIRCHHOFF
 v  0



i  0
Dominio
del Tempo
V  0



 I  0
68
Dominio
della Frequenza
EQUAZIONE DEI COMPONENTI
I(s)
a(t)
V(s)
V(s) = H(s) · I(s)
H(s) prende il nome di IMPEDENZA zs 
Nel caso di regime sinusoidale:
zs   z jw   z
Per questo caso esiste l'inversa della funzione di trasferimento:
1



y jw 
 y
AMMETTENZA
z jw 
VALORE EFFICACE. In elettrotecnica si utilizzano spesso i valori efficaci
delle grandezze sinusoidali, soprattutto quando si parla degli aspetti energetici.
Il valore efficace è definibile per tutte le grandezze periodiche:
VALORE EFFICACE =
1 T 2
f t dt

0
T
Nel caso sinusoidale:
Veff 
1 T 2
V sin 2 wt   dt

0 M
69
T
RESISTORE
v  R i  V  R  I
z  R
1
y   G
R
p(t)
I
z
RI2
V
pulsazione 2w
t
IL VALORE V·I E' IL VALORE MEDIO DI p(t) NEL PERIODO E
VIENE CHIAMATO POTENZA ATTIVA
70
CAPACITORE
dv
iC
 I  jw C V  jw 
dt
V
1
 z jw  
y  jw C
I
jw C
i
C
v
V I
p(t)
I
t

2
V
pulsazione 2w
La quantità Q = V·I pari all'ampiezza massima dell'oscillazione della potenza istantanea
è detta POTENZA REATTIVA.
71
INDUTTORE
di
vL
 V  jw L  I  jw 
dt
V
1
 z jw   jw L
y 
I
jw L
L
i
v
RAPPRESENTAZIONE FASORIALE
V

2
V I
V è in anticipo di p /2 rispetto a I
I
p(t)
t
pulsazione 2w
La potenza istantanea è una
sinusoide di pulsazione doppia
rispetto a tensione e corrente.
LA POTENZA ATTIVA E' NULLA
Q = V·I POTENZA REATTIVA
72
MUTUA INDUTTANZA
i1
M
L1
v1
i2
L2
di1
di2

v

L

M
1
12
 1
dt
dt

v2  L2 di2  M 21 di1

dt
dt
v2
M
k
i1
v1
M
i1
L1 L2
v2
v1
a) M > 0
I regime sinusoidale:
 V1  jwL1I1  jwM12 I 2



V2  jwL2 I 2  jwM 21I1
Hp:
M 12  M 21  M
L1L2  M 2  0
passivo
COEFFICIENTE DI ACCOPPIAMENTO ( k  1)
L1L2
i2
non dissipativo
M
i1
i2
L1 L2
b) M > 0
v2
v1
M
i1
i2
L1 L2
c) M < 0
v2
v1
M
i2
L1 L2
v2
d) M < 0
Se inizialmente si è nello stato zero, jwL1 , jwL2 e
jwM sono delle impedenze W.
LA MUTUA A 4 TERMINALI HA LE STESSE
EQUAZIONI DI QUELLA A 3 TERMINALI
73
TRASFORMATORE IDEALE
Se k = 1 (accoppiamento stretto)
M  L1L2
di1
di2

v

L

L
L
1
1
1
2

dt
dt

v2  L1L2 di1  L2 di2

dt
dt
di1
di2

v

L

L
L
1
1 2
 1
dt
dt
 
L
di
di
 1 v2  L1 1  L1L2 2
dt
dt
 L2
 v1 
L1
 v2  n  v2
L2
Nel dominio della frequenza:
 V1  jwL1I1  jw L1L2 I 2

 L1
V2  jwL1I1  jw L1L2 I 2

 L2
Per L1 , L2   si può trascurare il termine
 V1  nV2


1
 I1   I 2
n

I1
1 V1
L

 2
I 2 jwL1 I 2
L1
 V1  n V2
1 V1
jwL1 I 2
mentre
I1
TRASFORMATORE IDEALE
L2 1

da cui:
L1 n
I2
n:1
V1
V2
74
TEOREMI DI THEVENIN E NORTON
I
RETE
ATTIVA
Rete attiva costituita da componenti lineari
tempo-invarianti
V
I
zeq
THEVENIN
Eeq
EQUIVALENTE
CIRCUITALE
V
V  zeq I  Eeq
Il duale è il teorema di Norton
I
NORTON
Aeq
y eq
V
EQUIVALENTE
CIRCUITALE
I  yeq V  Aeq
75
PARTITORI
PARTITORE DI TENSIONE:
zi
z2
z1
Vi
I
E
Vi  zi  I
zi


V

E




i

E

z

I


 zi

i

i
 i 

PARTITORE DI CORRENTE:
z n
y1
V
y n1
y 2
y n
A
 I i  y i V
y i



  Ii  A  

A

y

 yi
 i  V

i
 i 

n=2
n=2
I
U1
U
U2
z1
z1
z1  z2
z2
U2  U 
z1  z2
z2
U1  U 
I2
I1
y1
y1
y1  y 2
y 2
I2  I 
y1  y 2
I1  I 
y 2
76
POTENZE IN REGIME SINUSOIDALE


i t   2  I  cos wt  e 2  I  e
 I  I e
V
z  z  e jj
V  z  I  z  e jj  I  e j 0  z  I  e jj
vt   e 2  zI  e jj e jwt  2V coswt  j 
pt   v  i  2V coswt  j   2 I cos wt  2VI coswt  j  cos wt
ma : 2 coswt  j  cos wt  cos j 1  cos 2wt   sin j sin 2wt
pt   VI  cos j 1  cos 2wt   VI  sin j sin 2wt
S
I
j0
z

VI·sinj

j wt
j
Potenza Attiva istantanea Potenza Reattiva istantanea
valore medio
valore massimo
VI cos j
P  VI cos j
Q  VI sin j
TRIANGOLO
Potenza Attiva [ W ]
Potenza Rettiva [ VAR ]
DELLE POTENZE
S  P  jQ Potenza Complessa


S  P 2  Q 2  V 2 I 2 cos 2 j  sin 2 j  VI Potenza Apparente [VA]
77
CASI PARTICOLARI
pt   VI 1  cos 2wt   RI 2 1  cos 2wt 
RESISTORE j = 0
valore medio: P = VI
Q=0
p(t)
I
V
RI 2
t
I
pt   VI sin 2wt
CAPACITORE j = /2 anticipo
p(t)
I
VI
I
V
t
p(t)

2
VI
V

2
V
P=0
Q = -VI
pt   VI sin 2wt
INDUTTORE j = /2 ritardo
I
V
t
I
V
P=0
Q = VI
78
TEOREMA DI BOUCHEROT
'
''
Dal teorema di Tellegen:  vh  ih  0
h
In regime sinusoidale:
Vh  ; I h* 
 
Applichiamo Tellegen agli insiemi delle Vh  e I h*
*
V

I
 h h   Ph  jQh   0
h
h
Affinché sia verificata deve essere:
 Ph  0
h
 Qh  0
h
79
RIFASAMENTO
2
2
E
E
IL
P
cos j ; Q 
sin j
z
z
z  z  e jj
IL
E
E
jwCE
z
Per Boucherot:
I L'
Qg  Qc  Qz  0
IL
IL 
I L'
jwCE
E
IL
z
RIFASARE SIGNIFICA IMPORRE:
E
j
E
sin j
z
Qg = 0 CIOE': Qc + Qz = 0
E2
E2
 
Qz 
sin j ; Qc 
sin     wCE 2 
z
1 wC  2 
C
sin j
z w
LA CAPACITÀ DIPENDE SOLO DAL CARICO E DALLA PULSAZIONE

1

 E jwC 
jj


z

e

IN FASE CON E
I L'


 E cos j
cos
j

j
sin
j
  E  jwC 





z
z



(GENERALMENTE cos j'  0,9 )
80
METODI ABBREVIATI DI ANALISI
METODO DELLE CORRENTI CICLICHE
Discende dalle equazioni di Maxwell 
Solenoidalità delle Correnti
Si introducono delle correnti fittizie che
siano di per sé solenoidali (base vettoriale
su cui si proiettano le correnti reali I )
Es:
z6
I4
E1
I1
M = l – (n - 1)
A
z4
z1 J A
I2
I5
z5
J B I3
E2
 z11
 z
Z    21
 

 z M 1
z12
z 22

z M 2
z1M 
 z 2 M 
 

 z MM 

zij  z ji
zii Impedenza propria della maglia i
z ji Impedenza mutua tra le maglie i e j
della maglia i
I6
JC
Z  J  E
z3
 J1 
J1     
 J 2 
Correnti cicliche
Nelle maglie
 Ev1   Ei1 
E         
 EM 1   EiM 
81
METODO DEI POTENZIALI NODALI
SI BASA SULLA PROPRIETA’ DI IRROTAZIONALITA’ DELLE TENSIONI
 E  dl  0
A3
1
A1
2
Y1
U2
U1
Qualsiasi tensione di lato è esprimibile
come somma algebrica dei potenziali
di nodo.
3
Y2
Y3
E
Y4
Legge di Kirchhoff delle tensioni
A2
U3
LE U 2 COSTITUISCONO UNA
BASE PER LE TENSIONI
Y U   A
 Y11 Y12  Y1N 


Y     
 
YN 1 YN 2  YNN 


 U1 
 
U     
U N 
 
 Ai1   Av1 
A        
 AiN   AvN 
82
ADATTAMENTO ENERGETICO
z g
A
A
Rete
Attiva
zC
Per il T. di Thevenin
I
zC
E V
B
B
Quali sono le condizioni nelle quali zC assorbirà la max potenza attiva?
E
E  zC
I
; V 
; zC  RC  jX C ;
z g  zC
z g  zC
2
E
E  zC
E
*

S  P  jQ  V  I 


 zC
*
2
z g  zC z g  zC 
z g  zC
*

P  e S 
zC  z*g
E
2
z g  zC
2
E2
 zC 
 RC
2
2
Rg  RC   X g  X C 
83
Analisi dei Transitori
84
1
1
0.9
0.8
0.8
0.6
0.7
0.4
0.6
0.2
volt
Volt
Obiettivo:
Descrivere il comportamento di tensioni e correnti
tra due diversi stati stazionari
0.5
0
0.4
-0.2
0.3
-0.4
0.2
-0.6
0.1
-0.8
0 0
1
2
3
4
tempo (s)
5
6
7
-10
1
2
3
4
5
6
7
tempo (s)
Causa del transitorio:
I componenti dotati di memoria (induttori e
condensatori) impiegano un certo tempo per
uniformarsi al funzionamento a regime
85
STATO INIZIALE NON NULLO
i
i
v
iC
dv
dt
v(0  )  0  V0
v
L
vL
di
dt
i (0  )  0  I 0
v’
v0
dv'
iC
dt
v ' (0  )  0
v  v'V0
t 0
i’
v
L
I0
di'
vL
dt
i ' (0  )  0
i  i ' I 0
t 0
Si introducono delle variabili scaricate
86
Circuiti lineari → Sovrapposizione degli effetti
E1
circuito
E1
E2
V1
E2
circuito
circuito
V2
V 1 V 2
Qualunque segnale periodico può essere espresso
come somma di sinusoidi (Serie di Fourier)
La risposta ad un segnale periodico si può calcolare
come somma delle risposte alle singole componenti 87
La funzione complessa che otteniamo prende il nome di
ampiezza
Trasformata di Fourier
w
fase
t
w
La sua espressione è:
F ( jw ) 


f t   e  jwt dt

88


IR
1  w 2 LC

U
1  w 2 LC  jwL
La funzione:
è il rapporto tra la


variabile di interesse e l’ingresso.
Come si vede, tale rapporto non dipende dall’ingresso, e
rappresenta quindi una caratteristica del circuito.
Essa prende il nome di Risposta in Frequenza e viene
descritta mediante il diagramma di modulo e di fase in
funzione della pulsazione (Diagrammi di Bode)
modulo
I diagrammi di Bode ci dicono come si
comporta il circuito alle diverse
frequenza.
fase
w
w
Le frequenze per cui si ha modulo alto
sono le frequenze che “passano”.
Le frequenze per cui si ha modulo
basso sono le frequenze che vengono
“filtrate”, ossia, un ingresso con tali
frequenze non produce una modifica
della variabile di uscita.
89
L’integrale F ( jw ) 


f t   e  jwt dt che definisce la trasformata di Fourier,

non si può calcolare per qualunque funzione.
In alternativa, anziché considerare la funzione come la somma di
sinusoidi, si può ottenere la stessa somma con le cisoidi
1
Le cisoidi seguono un andamento
oscillatorio smorzato.
0.8
0.6
Le cisoidi che permettono di ricostruire
una data funzione hanno lo stesso
inviluppo e frequenze multiple della
fondamentale.
0.4
0.2
0
-0.2
-0.4
Le sinusoidi sono particolari cisoidi, con
smorzamento nullo.
-0.6
-0.8
-1
0
0.5
1
1.5
2
2.5
3
La cisoide si ottiene moltiplicando un esponenziale per una sinusoide:
g t   e a t  cosw  t 
oppure:
g t   ea t  e jwt  ea  jw t  e st
90
Quanto detto finora sulla trasformata di Fourier vale anche per questa
nuova trasformata, ove si sostituisca la variabile immaginaria pura jw,
con la variabile complessa s=a+jw.
La nuova trasformata prende il nome di Trasformata di Laplace, e si
definisce come:

 st
F ( s)   f t   e dt
0
Come si può notare, l’integrazione non parte più da -.
Questo perché la funzione esponenziale che compare nella funzione
integranda ha modulo diverso da 1. In genere l’integrale converge se a
è <0, in modo che l’esponenziale sia decrescente. Ma in questo modo,
la stessa funzione diverge per t → -.
Questo è il motivo per cui si può calcolare la trasformata di Laplace
solo per funzioni che sono nulle per t<0. In questo modo l’integrale si
può calcolare solo per t0.
91
1
2
R
\ IR
Nel circuito si sostituisce la variabile s
in luogo di jw nei componenti dinamici.
IL
1
sC
sL
U
VC
IC
3
3
 IR  IL  IC

  VC
1

I R 
 sC  VC


V

sL

I


I

 C

sL
L
C
sC

VC  U  R  IR
 R  IR  VC  U
 sL  IR  1  s 2 LC  U  1  s 2 LC  IR
 1  s 2 LC  sL  I  1  s 2 LC  U

 IR




R

1  s LC  U

1  s LC   sL
2
2


2
1

s
LC 

 IR 
U  R  IR 
sL



IR
1  s 2 LC
H s  


U
1  s 2 LC  sL


Funzione di Trasferimento
Le Trasformate e le Anti-Trasformate si calcolano mediante le funzioni notevoli
92
Trasformate Notevoli
Funzione del tempo
d t 
d 1 t 
e  at  d 1 t 
sin wt   d 1 t 
coswt   d 1 t 
e  at  sin wt   d 1 t 
e  at  coswt   d 1 t 
Trasformata
1
1s
1
sa
w
s2  w 2
s
s2  w 2
w
s  a 2  w 2
sa
s  a 2  w 2
Per calcolare l’Anti-Trasformata dobbiamo scomporre la funzione di s
in una somma di funzioni di cui conosciamo la trasformata
93
Sistemi Trifase
94
per m=3
Sistemi Trifase
Sistema Diretto


 a1 (t )  2 A cost

2
)
a2 (t )  2 A cos(t 
3

a (t )  2 A cos(t  4 )
 3
3
A3

A1
Sequenza dei ritardi

A2
Rappresentazione
fasoriale
I TRE FASORI SI SUSSEGUONO SEGUENDO IL VERSO ORARIO
Sistema inverso
Antiorario
sequenza degli anticipi
95
Utilità dei sistemi trifase
Impiego: Produzione, trasporto, distribuzione, utilizzazione
(i sistemi monofase sono impiegati in applicazioni specifiche
come impianti di piccola potenza, per uso domestico,
trazione, elettrochimici, etc.)
Utilità:
A parità di tensione, potenza trasportata e perdite
ammesse, col trifase si utilizza un volume di rame inferiore
del 25%
Pd
Pd
P  VI cosj  3UI T cosj  PT  I T 
P
cosj
L 2
L 2
2
Pd  2 RI  2  I  3RT I T  3
IT
S
ST
I
3
2
Il volume di rame richiesto nei due casi e’:
PT
cosj
3
v  2 LS ; vT  3LS T  vT  v
4 96
Carichi Equilibrati
97
CARICHI SQUILIBRATI
La presenza di carichi non trifase puo’ introdurre uno
squilibrio nelle correnti. Es. Utilizzatori monofase come
quelli domestici
I guasti possono introdurre squilibrio nelle correnti
Fra fase e fase
Guasti:
Fra fase e neutro (Terra)
Fra fase-fase e neutro (Terra)
Il caso dei guasti è il più importante perché coinvolge grandi potenze
Lo squilibrio dovuto ai carichi monofase, almeno nelle grandi reti, può
essere compensato
SQUILIBRIO DOVUTO A CARICHI MONOFASE
Tra centro stella del carico e centro stella del generatore viene persa
la equipotenzialità. Si verifica uno spostamento del centro stella
98
METODO DELLO
SPOSTAMENTO DEL CENTRO STELLA

E1
I1

E2
o
I2
1
2

I3
E3
3
o’
Vo 'o
E1 E 2 E3




Z1 Z 2 Z 3

1
1
1




Z1 Z 2 Z 3
Teorema di Millmann
E1  Vo 'o
E2  Vo 'o
E3  Vo 'o
; I2 
; I3 
da cui: I1 


Z1
Z2
Z 3
Se le tensioni sono simmetriche,il diagramma fasoriale e’:
E3
U23
E2
E’3 o’
U31
Vo’o
E’1
o
E’2
U12
E1
Il centro stella del carico e’ spostato
rispetto al centro stella del
generatore
99
POTENZE NEI SISTEMI TRIFASE
NEUTRO ACCESSIBILE
A
IA
B
IB
C
IC
Potenza istantanea
p (t )  vA iA  vB iB  vC iC
N
In regime sinusoidale
P  VA I A cos jA VB I B cos jB VC IC cos jC
Q  VA I A sin jA VB I B sin jB VC IC sin jC
S  P  jQ
S  P2  Q2
100
Inserzione Aron
1
 
P"  V32 I3 cosV32 I3 
P'  V12 I1 cos V12 I1
W’
2
3
P  P' P' '
Q  3 P' ' P'
W”
3
I3
E3
I2
U 23
2
U 12
U 31
E1
j
U 12
E2
I1
30
1
j
I1
U 32

y1
E1
E3
30  y 2 I 3
j
101
RIFASAMENTO DEI CARICHI TRIFASE
Carico
P  P'
Qc  Q  Q'
Qc  P tan j  P tan j' 
Batteria di
condensatori
102
Collegamento a stella
U
Carico
CY
Collegamento a triangolo
U
Carico
E2
U2
 3CY
 CY U 2
QCY  3
XY
3
P (tan j  tan j' )
CY 
U 2
U2
 3C U 2
QC   3
X
P (tan j  tan j' )
C 
3U 2
C
1
C   CY
3
103
ELETTROMAGNETISMO
MODELLO IDEALE:
1. QUANTITA' DI BASE: SORGENTI E CAMPI
2. REGOLE DI OPERAZIONE: CALCOLO VETTORIALE
3. RELAZIONI FONDAMENTALI: EQUAZIONI DI MAXWELL
104
RELAZIONI MISTE FRA GRANDEZZE
B
SCALARI E VETTORIALI
V

Es: AB A E  d l
CAMPO MAGNETICO STAZIONARIO
I
B
r
P
I   H  dl
I 
Bm

I
2 r   H 
Legge di Biot-Savart
2 r

B  mH 
TEOREMA DELLA CIRCUITAZIONE
Um   H  dl  N  I
(Ampére-spire)
Applicando il Teorema di Stokes
rot H  J Legge di Ampére in forma locale
105
FLUSSO DI INDUZIONE
  S B  d s
APPLICANDO L'INTEGRALE AD UNA
SUPERFICIE CHIUSA:
B
ds
s B  d s  0 Legge di Gauss
B E' SOLENOIDALE
APPLICANDO IL TEOREMA DELLA DIVERGENZA: div B  0
• Diverse superfici che hanno lo stesso contorno, hanno lo stesso flusso
concatenato  Si parla di flusso concatenato con una linea chiusa
REGOLA DI MAXWELL
• Il verso positivo dell'asse della bobina è quello in
cui avanza una vite destrogira che ruota nel verso
positivo di percorrenza del filo
106
IPOTESI SUI MEZZI MATERIALI
CONTINUI - OMOGENEI - ISOTROPI - LINEARI
Caratterizzati dalle seguenti grandezze scalari:
g conduttività [ S / m ]
e permettività [ F / m ]
m permeabilità [ H / m ]
EQUAZIONI COSTITUTIVE DEL MEZZO:
D=eE
B=mH
COSTANTI UNIVERSALI:
•Velocità della luce nel vuoto
c  3·108 m / s
•Permeabilità del vuoto
m0 = 4 · 10-7 H / m
•Permettività del vuoto
e0 = 1/(36 · 10-9 F /
m
1
m
c
 299 792 458
s
m 0e 0
107
m r è funzione del campo magnetico e quindi dipende dal punto di lavoro
B = f (H) NON LINEARE
tan-1m0
B
Br
-Hmax
SATURAZIONE
-HC
HC
Hmax
H
-Br
HC: forza coercitiva
108
Br: induzione residua
Analogia con Legge di Ohm
I
 H  dl  N  I
L

L

B
m
(L. Ampére)
N
L
 dl  N  I


L m  S  dl  N  I
Analogia con la Legge di Ohm
R m = Riluttanza

dl

 N I
L m S
  R m  N  I
Gm = 1/R m = Permeanza
109
ANALOGIA
CIRCUITI MAGNETICI
CIRCUITI ELETTRICI
F.M.M. (f )
F.E.M. (E)
PERMEANZA G m
CONDUTTANZA G
RILUTTANZA R m
RESISTENZA R
FLUSSO 
CORRENTE I
Um = R m 
U = RI
S  0
SI = 0
S Um = SR m 
SV = S RI
110
CIRCUITI MUTUAMENTE ACCOPPIATI
i 1 M i2
v1
L1
L2 v2
di1
di2

 v1  L1 dt  M dt

di
di
v2  M 1  L2 2
dt
dt


V1  jwL1I1  jwMI 2


V2  jwMI1  jwL2 I 2
 Flusso Principale
I1
d1 Flusso Disperso Primario
N1
d2 Flusso Disperso Secondario
1 Flusso Concatenato con una Spira Primaria
2 Flusso Concatenato con una Spira Secondaria
 1     d 1

 2     d 2

 d1

  c1  N1  N1 d1


 c 2  N 2  N 2 d 2
I2
d 2
N2
111

  c1  N1  N1 d1


 c 2  N 2  N 2 d 2
  G mN1I1  N 2 I 2 

 d1  G d1N1I1 
  G N I 
d2
2 2
 d2

ma:
Gm permeanza del circuito magnetico
Gd1 permeanza costante (percorso in aria)
Gd2 permeanza costante (percorso in aria)
 c1  N1G mN1I1  N 2 I 2   N1G d1N1I1 

 c 2  N 2G mN1I1  N 2 I 2   N 2G d 2N 2 I 2 
poniamo:
 L1  N12 G d 1 G m  Induttanza propria del circuito 1

2
 L2  N 2 G d 2  G m  Induttanza propria del circuito 2
M  N N G
Mutua induttanza
1 2 m


 c1  L1  I1  M  I 2

 c 2  L2  I 2  M  I1
112
continua…
 c1  L1  I1  M  I 2

 c 2  L2  I 2  M  I1
di1
di2
 d c1

L


M

1
 dt
dt
dt
 d
di
di
 c 2  L2  2  M  1
dt
dt
 dt
Se siamo in condizioni dinamiche:

di1
di2

v

L


M

1
1
dt
dt

di
di
v2  L2  2  M  1
dt
dt

Si possono definire le induttanze di dispersione dei due circuiti.
Dalle
 cd1  N1 d 1  N12G m d1 I1  Ld 1  I1

2


N


N
2 d2
2 G m d 2 I 2  Ld 2  I 2
 cd 2
 Ld 1  N12G m d1
 
2
L

N
2 G m d2
 d2
113
CIRCUITI EQUIVALENTI
ΦC1  N12 G md1  G m I1  N1 N 2G m I 2

2
Φ

N
N
G
I

N
1 2 m 1
2 G md 2  G m I 2
 C2
Ponendo:
N12G md1  Ld 1
induttanza di dispersione primaria
N 22G md 2  Ld 2
induttanza di dispersione secondaria
N12G m  Lm
induttanza di magnetizzazione


N2 
2

I 2 
ΦC1  Ld 1 I1  N1 G m  I1 
N1 



Φ  L I  N 2G  I  N1 I 
d2 2
2 m 2
1
 C 2
N
2



N1

N2
114



N
2
I 2 
ΦC1  Ld 1 I1  Lm  I1 

N1 


 N1 Φ  N1  N1  N 2 L I  N1 N 2 N1  N 2 G  I  N1 I 
 N 2 C 2 N 2 N 2 N1 d 2 2 N 2 2 N 2 N1 m  2 N 2 1 



I
2
ΦC1  Ld 1 I1  Lm  I1  n 

N1



n

rapporto spire
N2
nΦ  n 2 L I 2  L  I  I 2 
d2
m
1
 C 2
n
n

I1
DOPPIO BIPOLO EQUIVALENTE
2
Ld1
I2
n L
d2
n
 c1
Lm
I1 
I2
n
n  c2
2
n Ld 2
I2
n
n  c2
grandezze
secondarie
riferite al
primario
115
TRASFORMAZIONE DELLE IMPEDENZE
I1
n:1
V2
V1
I2
V2 V1 1
1 V1

 
 2
I 2 n n I1 n I 1
1 '
 2 Z2
n
Z 2
Z 2
Un’impedenza Z 2 applicata ai morsetti secondari di un trasformatore
ideale puo’ essere sostituita da un’impedenza Z 2'  n 2 Z 2 ai morsetti
primari senza che il funzionamento complessivo
venga alterato, e
n
viceversa.
RIASSUMENDO:
2
per portare una grandezza secondaria al primario:
Tensione : V2'  nV2 ; Corrente : I 2' 
I2
; Impedenza : Z 2'  n 2 Z 2
n
per portare una grandezza primaria al secondario:
Tensione
: V1"
1
1 
 V1; Corrente : I1"  nI1; Impedenza : Z1"  116
Z
2 1
n
n
Ricordando il significato delle varie induttanze

  G m N1 I1  N 2 I 2 
G m : permeanza del circuito magnetico
 : flusso principale
 d 1  G d 1 N1 I1 : flusso disperso primario
 d1  d 2
 d 2  G d 2 N 2 I 2 : flusso disperso secondario
Ld 1
Ld 2
n:1
Lm
117
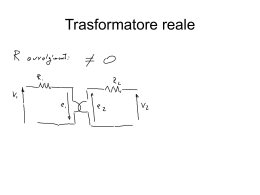
Trasformatore Reale
m 
Hp:
Ferro Ideale
Pfe=0
accoppiamento perfetto
Rame Ideale
TRASFORMATORE
IDEALE
Pcu=0
Il circuito equivalente del trasformatore reale si ottiene
rimuovendo le ipotesi di ferro ideale e di rame ideale
118
CIRCUITO EQUIVALENTE
I1
V1
X d1
R1
 E1
X 'd 2
If
I0
Im
G B
 E 2'
R'2  I '2
 I2
V2
V2'
R1: resistenza equivalente dell’avvolgimento primario
R’2=n2R2 con R2 resistenza dell’avvolgimento secondario
Xd1=Ld1 con Ld1 induttanza di dispersione primaria
X’d2=n2 Xd2 ; Xd2=Ld2 con Ld2 induttanza di dispersione secondaria
G: conduttanza trasversale (mette in conto le perdite nel ferro)
B=1/Xm; Xm=j Lm con Lm induttanza di magnetizzazione
I0: corrente a vuoto
Im: corrente magnetizzante
E’2=nE2
119
PROVA A VUOTO
o Trascurando le perdite di eccitazione R1I02 rispetto a quelle nel ferro
GE12 (rapporto di poche unità per mille)
o Trascurando la potenza reattiva richiesta per l’eccitazione del flusso
disperso rispetto a quelle necessarie a sostenere il flusso principale
Il circuito equivalente del trasformatore nel funzionamento
a vuoto e’ il seguente:
I0
Y  G  jBm
I0
V1   E1
If
Im
G B
W
V20
Ammettenza a vuoto
primaria
A
V
T
V
120
W
A
V1
T
wattmetro
amperometro
voltmetro
V2
P0
I0
V1n
V1  f ( I 0 )  curva normale di magnetizza zione
I0
V1  B
I 0  f .m.m.
P0
P0
I0
P0  f (V1 ) parabola
2
 V12
Pfe  BM
I
Y  0
V1n
 Bm  Y 2  G 2
P
G  02
V1n
V1 n
V1
In corrispondenza alla tensione nominale, le letture degli strumenti
forniscono i dati sufficienti a ricavare i parametri trasversali del
circuito equivalente del trasformatore: G e B
Spesso non e’ necessario effettuare la prova a vuoto in quanto121i dati
della prova vengono riportati nella TARGA del trasformatore
PROVA IN CORTO CIRCUITO
W
V1
Pcc
I1n
A
V
Pcc
T
V1  f ( I1 ) e’ circa una retta passante
per l’origine
V1
' 
'
Z cc
X cc
I 1n
V1cc  I1n
I1
'
R
( cc piccolo)
'
X cc
dipende dalle riluttanze dei circuiti
magnetici percorsi dai flussi dispersi
costanti perche’ prevalentemente in aria
 2
Pcc  f ( I1 ) parabola: Pcu  Pcc
I
In corrispondenza della corrente nominale:
'  V1cc
'  Pcc 
' 
'2  '2


Z cc
; Rcc
X
Z
cc
cc Rcc
2
I1n
I1n
I dati vengono riportati nella targa: V1cc ; Pcc
122
FUNZIONAMENTO A CARICO
X d1
I1
R1
X 'd 2
R '2  I '2
n:1
I0
 E1
V1
I
f
Im
G B
V1
R1 I 1
 E1
I0
Im
'
V 2'
I2
'
'
R2 I 2
jX
'
'
d 2I2
 E 2'
Note:
jX d 1 I 1
I1
 I 2'
If

 I2
V2
V 2'
V2 ; I 2
  E 2'  V 2'  ( R 2'  jX d' 2 ) I 2'

'



E
E
 1
2   nE 2

 I 0  I m  I f   (G  jB ) E1
 
E1  ( R1  jX d 1 ) I1
V1
 I 1  I 0  I 2'
E2
123
MACCHINE ELETTRICHE
ROTANTI
124
Generatori e Motori
Macchine Elettromeccaniche

d
0
dt
Pel
M
Pp
Pmecc  Pel
Pmecc
h
Pel
I
forze meccaniche
moto relativo
motore
f.e.m.
Pmecc
generatore
Pmecc
Pel
G
Pp
Pel  Pmecc
Pp = Prame + Pferro + Pmeccaniche
Pel
h
Pmecc
125
traferro
statore
rotore
Elementi essenziali:
Circuito magnetico
Avvolgimenti
Organi di presa corrente
macchina rettificata
N
S
S
passo
polare
N
Bmax
Generatore:
Si trascina il rotore
L’indotto è sede di una fem
Motore:
I due circuiti sono percorsi da corrente
Il campo di rotore insegue quello di statore
Il rotore è trascinato
126
Macchine in Corrente Continua - 1
Avvolgimento rotorico
Rotore
Morsetti
S
Contatti striscianti (spazzole)
N
Collettore (collega gli avvolgimenti con l’esterno)
Funzionamento da motore:
Si alimenta il rotore con una tensione continua attraverso i
morsetti.
L’avvolgimento di rotore è attraversato da una corrente
alternata, perché il collettore inverte la polarità ogni mezzo giro
Il campo magnetico del rotore è alternato, ed insegue il campo
magnetico stazionario dello statore, trascinando il rotore.
f.e.m. rotore
Funzionamento da generatore:
Trascinando il rotore, il suo avvolgimento si concatena con un
flusso variabile, quindi è sede di una f.e.m. indotta.
Ogni mezzo giro la polarità dei morsetti si inverte, dando luogo,in
uscita, ad una tensione unidirezionale
f.e.m. ai morsetti
127
Macchine in Corrente Continua - 2
N
Anello di Pacinotti
Lamella conduttrice
S
Collettore a lamelle
Aumentando il numero di commutazioni
per giro, la f.e.m. ai morsetti
diventa sempre più continua
128
Macchine sincrone - Generatore
a
b
c
c
b
a
passo polare
rotore con 1 avvolgimento
rotore con 3 avvolgimenti
Opzione 1: il rotore è alimentato in c.c. e trascinato
da un motore primo. L’avvolgimento o gli avvolgimenti
di statore sono sede di f.e.m. indotte sinusoidali.
Opzione 2: lo statore è alimentato in c.c. ed il
rotore è trascinato. L’avvolgimento di rotore diventa
il circuito indotto, da cui si preleva la potenza
attraverso i contatti striscianti.
Se l’indotto ha un solo avvolgimento, la f.e.m. indotta è monofase
129
Se l’indotto ha tre avvolgimenti, la f.e.m. è trifase
a
b
Macchine sincrone - Motore
a
b
c
c
c
b
a
 I 3 avvolgimenti statorici sono alimentati con 3 tensioni sfasate tra loro di 120°
 I 3 campi sinusoidali si combinano, dando luogo ad un campo magnetico rotante
 Il rotore è alimentato con una corrente continua. Il campo da essa generato
tenterà di allinearsi con il campo rotante di statore, trascinando il rotore.
+
130
a
Macchine asincrone - Motore
a b c
b
Lo statore è alimentato come
avviene nel motore sincrono,
dando luogo ad un campo
magnetico rotante
c
c
b
Coppia
a
 Nel rotore l’avvolgimento è chiuso in corto circuito
 Il campo di rotore induce una f.e.m. nelle spire del rotore, con
conseguente circolazione di corrente.
 Il campo di rotore che ne deriva tende ad allinearsi con il
campo di statore, trascinando il rotore ad una velocità minore
di quella del campo di statore (scorrimento)
 Se il rotore gira alla velocità del campo di statore
(sincronismo), il flusso concatenato con le spire di rotore è
costante, la corrente indotta si annulla, e quindi anche la coppia
 La velocità di rotazione è determinata dall’incontro della coppia
motrice e del carico
ns
n
Spesso l’avvolgimento di rotore è
realizzato con barre cortocircuitate
agli estremi, a formare la tipica
gabbia di scoiattolo 131