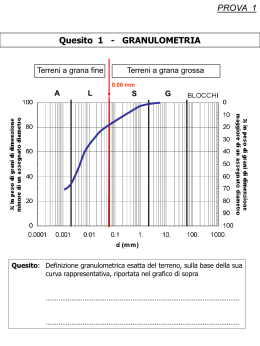
www.matematicamente.it
Centro di DIDA
Dip. Ing. Innov.- Università del Salento
Kataweb
Gruppo Editoriale L’espresso
_______________________________________________________________________________________
Matematicup, prima competizione nazionale di matematica a squadre, completamente su Internet
Caro collega,
diversi documenti storici ci confermano che l'insegnamento della matematica è efficace quando è
accompagnato da una sfida tra l'allievo e un quesito ben formulato che lo attrae. L'allievo ha la sensazione
che sia facile, alla sua portata, che lo risolverà in un lampo e senza accorgersene si addentra nei meandri del
pensiero, del ragionamento, del calcolo, della rappresentazione grafica … e scoprirà di aver fatto
matematica.
Già 4000 anni fa, come risulta dal Papiro di Rhind, in Egitto la matematica si insegnava per problemi.
Problemi dalla formulazione semplice, che fanno riferimento a oggetti della vita comune, che attraggono e
incuriosiscono. Uno di questi recita "Ci sono sette case, in ogni casa ci sono sette gatti, ogni gatto mangia
sette topi, ogni topo mangia sette spighe, ogni spiga produce sette hekath di grano, quanti sono in tutto?"
Chi non ha mai sentito questo indovinello? Magari con personaggi diversi. Tenendo conto che il papiro su cui
è trascritto è stato ritrovato soltanto 150 anni fa, si può ritenere che questo problema ha attraversato
quattro millenni, duranti i quali l'umanità lo ha tramandato o lo ha riscoperto più volte. Il metodo di
insegnamento che il problema si porta dietro ha superato la diversità delle culture, dei mezzi di
comunicazione, degli strumenti di scrittura, del simbolismo matematico e proprio per questo rimane un
punto di riferimento per chi vuole insegnare la matematica.
Per citare un altro caso storico, ricordo il libretto di Alcuino di York, ora tradotto anche in italiano, Problemi
per rendere acuta la mente dei giovani, Edizioni ETS. Alcuino di York era un monaco inglese che nel 781
venne chiamato alla corte di Carlomagno per istruire i giovani nobili. In quel periodo raccolse una serie di
problemi divertenti e stimolanti la cui origine si perde nella notte dei tempi. Uno di questi recita: “Un uomo
doveva trasportare aldilà di un fiume un lupo, una capra e un cavolo e non poté trovare altra barca se non
una che era in grado di portare soltanto due di essi. Gli era stato ordinato però di trasportare tutte queste
cose di là senza alcun danno. Chi è in grado dica in che modo poté trasferirli indenni”. Chissà quante volte ti
hanno proposto o hai proposto questo quesito. L’espressione “salvare capra e cavoli” deriva sicuramente da
questo antichissimo quesito, ormai sedimentato nella nostra cultura e tramandato di generazione in
generazione. Il monaco Alcuino aveva visto, in questo metodo 'popolare' di insegnare, la via per introdurre i
giovani allo studio della matematica.
Un ultimo episodio che voglio ricordare è la gara di matematica a squadre del 1223 a Pisa, alla presenza
dell’imperatore Federico II di Svevia. Uno dei quesiti della gara era il seguente: "Un tale chiude una coppia di
conigli tra quattro mura. Quante coppie potranno essere generate in un anno, supponendo che ogni mese
ognuna delle coppie genera una nuova coppia che comincia a procreare dal secondo mese di vita?". La gara
fu vinta da Fibonacci, il quale rispose in maniera così rapida che molti pensarono a un imbroglio. Da questo
quesito sono venuti fuori i famosi numeri di Fibonacci che occupano un posto di rilievo nella matematica e
nelle sue applicazioni.
In un momento in cui tutti lamentiamo uno scarso interesse dei giovani verso la matematica questi
significativi momenti storici ci indicano la soluzione: ripercorrere le vie dei grandi maestri del passato e
recuperare la tradizione delle dispute matematiche per fare apprezzare ai giovani di oggi il piacere del
pensare corretto.
Quale migliore occasione allora per unire la tradizione delle sfide di matematica con l'innovazione tecnologica
di Internet. Ti invito perciò a indossare la maglia di allenatore e formare la squadra vincente della tua scuola.
Lecce, 14.3.2007
Antonio Bernardo
www.matematicamente.it