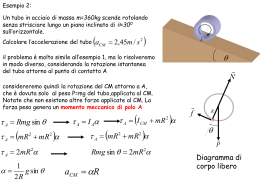
Esempio
Un disco rigido omogeneo di massa M=1,4kg e raggio
R=8,5cm rotola su un piano orizzontale alla velocità di
15cm/s. Quale è la sua energia cinetica?
n.b.: Parlando di velocità di un oggetto rotolante si intende
sempre la velocità lineare del C.d.M
Rotolare giù per una discesa:cont.
Equazione del moto di
traslazione del CM
f s  Mg sin   Macm
Equazione del moto di
rotazione attorno al CM,
dovuta alla fs
 s  Rf s  I cm
Il corpo rotola senza
strisciare,quindi il moto è
volvente
sostituendo
=-a/R
acm=-R
f s   I cm
acm
2
R
Sostituendo fs , nella equazione del moto di traslazione del CM.
 I cm
acm
 Mg sin   Macm
2
R
acm
g sin 

2
1  I cm / MR


Esempio 2:
Un tubo in acciaio di massa m=360kg scende rotolando
senza strisciare lungo un piano inclinato di =300
sull’orizzontale.
Calcolare l’accelerazione del tubo
a
CM
 2,45m / s 2

A

il problema è molto simile all’esempio 1, ma lo risolveremo
in modo diverso, considerando la rotazione istantanea
del tubo attorno al punto di contatto A
considereremo quindi la rotazione del CM attorno a A,
che è dovuta solo al peso P del tubo,applicata al CM.
Notate che non esistono altre forze applicate al CM. La
forza peso genera un momento meccanico di polo A
 A  Rmg sin 
 A  mR2  mR2 
 A  2mR2

1
g sin 
2R
 A  I A
 A  I CM  mR 2 
 A  mR2  mR2 
Rmg sin   2mR2
aCM  R

N

f
R


P
Diagramma di
corpo libero
Un tubo in acciaio di massa m=360kg scende rotolando
senza strisciare lungo un piano inclinato di =300
sull’orizzontale.
Quanto vale il modulo della forza di attrito nel punto di
contatto tra tubo e piano inclinato?

Utilizzeremo il risultato appena ottenuto , nell’equazione
del moto di traslazione del CM
f s  mg sin   macm
a
CM
 2,45m / s 2
f s  883N


N
Diagramma di
corpo libero

f
R


P
Un tubo in acciaio di massa 360kg scende rotolando senza
strisciare lungo un piano inclinato di 300 sull’orizzontale.
Si supponga che il tubo , inizialmente in
quiete,percorra rotolando 3m lungo il piano
inclinato. Quanto vale la sua energia cinetica
totale in questo istante? Quanto la energia
cinetica di traslazione e di rotazione interna?
A

L’energia cinetica totale è
semplicemente l’energia di rotazione di
tutto iltubo attorno all’asse istantaneo
passante nel punto A
K

v 2  v02  2ax
la variazione della velocità in funzione dello spazio
percorso e della accelerazione costante è
dato che il tubo
parte dalla
quiete
v  3,84m / s; K  5,30 103 J
v0  0; v  2ax
L’energia cinetica di
traslazione
K trasl 
L’energia cinetica di
rotazione interna
K int 

1 2 1
2
I  2mR 2 v / R   mv 2
2
2
1 2
1
mvcm  mv2
2
2

 2,65 103 J

1
1
1
2
I cm 2  mR 2 v / R   mv 2
2
2
2
 2,65 103 J
osservazioni e verifiche
1 2
mv
2
1
K int  mv2
2
K  mv2
K trasl 
L’energia cinetica rotazionale e quella
traslazionale si sommano, ottenendo l’energia
v 2  v02  2ax
v  2ax
cinetica totale


v  2ax  2  2,45m / s 2  3,0m  3,84 J


K  mv 2  360kg  3,84m / s 2  5,3  103 J
K int  K trasl  2,65  103 J
L’energia cinetica totale è
uguale alla variazione
dell’energia potenziale
gravitazionale


U  mgh  360kg  9,81ms2  3,0m  sin 300
U  5,30 103
Ciò indica che la forza di attrito non compie lavoro. Infatti il punto della ruota nella quale
agisce la forza di attrito è il punto di contatto,che è istantaneamente in quiete e non subisce
spostamento nella direzione della forza di attrito
Uno yo-yo moderno ha il filo arrotolato sul mozzo
Quando uno yo-yo rotola giù lungo il filo perde energia potenziale ma
aumenta la sua energia cinetica sia di traslazione che di rotazione.
1
1
2
E  mgh  m cm
 I cm 2
2
2
per calcolre l’accelerazione lineare acm procedere come nel
primo esercizio di oggi (palla su piano inclinato, tenendo conto
che
la discesa è verticale: =900
lo yo-yo rotola sul mozzo con raggio R0, e non sulla sua
superficie esterna con raggio R
la forza che lo trattiene è la tensione T, e non l’ attrito f
acm 
g
2
1  I cm / mR0


Lo yo-yo
Un yo-yo è in quiete sul pavimento.
Uno strattone gentile è esercitato
orizzontalmente sulla corda in modo
che lo yo-yo rotola senza strisciare. In
che direzione si muove e perché?

F
P
Lo yo-yo rotola nella direzione del tiro.rotolando senza
slittare, il punto P ha una velocità istantanea nulla. La
rotazione attorno ad un asse fisso che passa per P è
determinata dal momento della forza rissultante. Solo F
ha un momento diverso da 0 Quindi la rotazione è nel
verso orario, e lo yo yo si muove in avanti