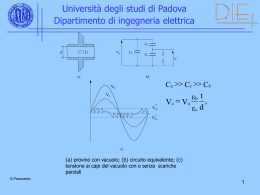
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Sovratensioni di manovra
Evento
Punto considerato
Chiusura di linee in assenza di
mezzi di controllo
All’estremità di manovra
2 ÷ 2,5
All’estremità aperta
2,4 ÷2,8
Richiusura trifase in assenza di
mezzi di controllo
All’estremità di manovra
2,3÷ 3
All’estremità aperta
3 ÷3,7
Richiusura monofase in assenza
di mezzi di controllo
All’estremità di manovra
1,5÷ 1,8
All’estremità aperta
1,8 ÷ 2,4
Chiusura di linee e richiusura
trifase con interruttori dotati di
resistore di preinserzione
All’estremità di manovra
1,6 ÷ 1,8
All’estremità aperta
1,7 ÷ 2,2
Chiusura di linee e richiusura
trifase con interruttori dotati di
più resistori di preinserzione
All’estremità di manovra
1, 2 ÷ 1,4
All’estremità aperta
1,5 ÷ 1,7
Apertura di linee a vuoto senza
riadescamenti
Lato linea dell’interruttore
manovrato
Apertura di linee a vuoto con
riadescamenti
Valori confrontabili con quelli della richiusura trifase in assenza di mezzi di
controllo
Apertura di trasformatori a vuoto
Lato trasformatore manovrato
Lato sbarre
G.Pesavento
Valore massimo della sovratensione
(p.u.)
1,3
2 ÷ 2,3
1
1
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
2
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Sovratensioni sostenute
Le sovratensioni sostenute sono transitori oscillanti poco smorzati a
frequenza di rete, o prossima ad essa con durate che possono variare,
secondo i dispositivi di protezione esistenti, da pochi periodi fino a
qualche secondo.
La loro importanza sta nel fatto che il loro valore massimo può
condizionare il livello di protezione di alcuni tipi di scaricatori che non
debbono intervenire al loro presentarsi, data l'energia che sarebbero
chiamati ad assorbire.
Esse, inoltre, possono risultare determinanti nella scelta dell'isolamento
in atmosfera contaminata.
• improvvise perdite di carico
• disinserzione di carichi induttivi o inserzione di carichi capacitivi
• chiusura di linee a vuoto
• guasti monofase a terra
• fenomeni di risonanza e autoeccitazione.
G.Pesavento
3
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
4
Università degli studi di Padova
Dipartimento di ingegneria elettrica
In generale le sovratensioni atmosferiche non finiscono mai con il prevalere
nel dimensionamento degli isolamenti; ciò è provato dal fatto che gli
isolamenti degli impianti differiscono molto quando le tensioni del sistema
sono diverse, ma assai poco quando i livelli ceraunici sono diversi. Infatti
per ridurre il rischio di scarica dovuto a sovratensioni atmosferiche, si
possono conseguire risultati migliori riducendo queste ultime, piuttosto che
rinforzando l'isolamento; ciò si ottiene perfezionando i sistemi di guardia
(parafulmini, funi di guardia) ed i sistemi di terra.
Chi determina quindi l'isolamento di un sistema elettrico sono le
sovratensioni interne (sostenute e di manovra) oltreché, naturalmente, la
tensione di esercizio; ma poiché le sovratensioni interne dipendono dalle
caratteristiche del sistema è sempre possibile modificare il sistema in modo
da ridurle, come indicato nello schema a blocchi. Naturalmente tali
modifiche saranno realizzate solo quando il loro costo risulti inferiore alle
economie realizzabili sull'isolamento e ciò può accadere solo fino al
momento in cui l'isolamento è determinato dalla tensione di esercizio.
Questa sollecitazione dielettrica torna quindi ad essere il vero fattore
G.Pesavento
determinante degli isolamenti di un sistema.
5
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Correnti di fulmine e frequenza di fulminazione
G.Pesavento
6
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Distribuzione cumulata dei valori di picco.
1) tutti i valori raggruppati 2) tutte le scariche negative;
3) prime scariche negative 4) scariche negative successive;
5) scariche positive
G.Pesavento
7
Università degli studi di Padova
Dipartimento di ingegneria elettrica
[kA/s]
Pendenze massime delle correnti
1) tutti i valori raggruppati; 2) tutte le scariche negative; 3) prime
scariche negative; 4) scariche negative successive; 5) scariche
positive
G.Pesavento
8
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
9
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
10
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Caso B
Caso A
Z
P
Z
R
Fulminazione di linea senza fune di guardia
Se if (t) è la corrente di fulmine, la tensione verso terra del punto P
risulterà vP (t) = Z/2 · if (t)
G.Pesavento
11
Università degli studi di Padova
Dipartimento di ingegneria elettrica
v(t)
z if(t)
2
vi
Rif(t)
t
Sovratensione dopo la scarica di una catena di
isolatori
G.Pesavento
12
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Fulminazione diretta di un traliccio
Z
R
2
V  If
Z
R
2
Fulminazione su linee con fune di guardia
Zg
2
V  If
Zg
R
2
R
G.Pesavento
13
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Il modello elettrogeometrico
Questo tipo di modello si basa sul concetto di “distanza di impatto” o
“striking distance”, ossia la distanza che si ha tra la punta del leader
discendente e una struttura a terra quando il campo elettrico medio in
essa raggiunge il valore critico di scarica. Finché il leader non arriva a tale
distanza da una struttura a terra il punto di impatto del fulmine non è
ancora definito. Il valore critico del campo medio di scarica viene valutato
dai diversi autori tra 3 e 6 kV/cm. Detta S la striking distance, è possibile
costruire la figura 9.10, nella quale G e C rappresentano, rispettivamente,
la fune di guardia e il conduttore di fase,  l’angolo di schermatura, c ed h
la posizione reciproca dei diversi elementi.
G.Pesavento
14
S  6,7
A IfbI0,8
f
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Il valore S della striking distance
dipende dalla carica nel leader
che, a sua volta, è legata in
qualche modo al valore massimo
If della corrente del fulmine.
Le relazioni tra S e If proposte
dai vari autori sono del tipo
e la più usata è
wp
A
S
G
B
D
S

c
S  A Ifb
C
h
S
S  6,7 I0,8
f
con S espressa in metri e If in kA.
ws
G.Pesavento
15
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Fissata la posizione di fune di guardia e conduttore, ossia i valori
di c,  e h, all’aumentare della corrente, e quindi di S, il valore di
ws diminuisce fino ad annullarsi per un certo valore Im; un
fulmine con corrente superiore a Im non colpirà mai il
conduttore.
Se Ng è il numero di fulmini che cadono al suolo per km2 e per
anno nella zona in cui esiste la linea ed f(If ) è la funzione densità
di probabilità dei valori della corrente di fulmine, il numero N,
per km2 e per anno, di fulminazioni dirette di un conduttore di
fase della linea
Im
N  Ng  2 w s (I)  f (I)dI
Ic
G.Pesavento
16
Università degli studi di Padova
Dipartimento di ingegneria elettrica
Modelli basati sulla propagazione del leader
vP1
1
ds
2
v+
df
Wp
C
H
G.Pesavento
17
Università degli studi di Padova
Dipartimento di ingegneria elettrica
V
X
A
B
C
O
D
t
Esempio di caratteristiche tensione di scarica-tempo alla scarica
G.Pesavento
18
Università degli studi di Padova
Dipartimento di ingegneria elettrica
TABELLA I
Tensione massima
di un elemento del sistema
[kV]
G.Pesavento
3,6
Tensione nominale
di tenuta a frequenza
industriale
[kV]
10
Tensione nominale
di tenuta ad impulso
atmosferico
[kVcresta]
20
40
7,2
20
40
60
12
28
17,5 (*)
38
75
95
24
50
95
125
145
36
70
145
170
52 (*)
95
250
72,5
140
325
60
75
95
19
Università degli studi di Padova
Dipartimento di ingegneria elettrica
TABELLA II
Tensione massima
di un elemento del sistema
[kV]
Tensione nominale
di tenuta a frequenza
industriale
[kV]
Tensione nominale
di tenuta ad impulso
atmosferico
[kVcresta]
100 (*)
150
185
185
230
185
230
275
230
275
325
275
325
360
395
460
380
450
450
550
450
550
650
550
650
750
650
750
850
950
1050
123
145
170
245
G.Pesavento
20
Università degli studi di Padova
Dipartimento di ingegneria elettrica
TABELLA III
Tensione massima
di un elemento del sistema
[kV]
300 (*)
Tensione nominale
di tenuta ad impulso di
manovra
[kVcresta]
750
850
362
850
950
850
420
950
1050
950
550
1050
1175
1300
800
1425
1550
1425
1100
1550
1675
1800
1675
1200 (**)
1800
1950
G.Pesavento
Tensione nominale
di tenuta ad impulso
atmosferico
[kVcresta]
850
950
950
1050
950
1050
1050
1175
1050
1175
1175
1300
1300
1425
1175
1300
1300
1425
1425
1550
1675
1800
1800
1950
1950
2100
1950
2100
2100
2250
2250
2400
2400
2500
2100
2250
2250
2400
2500
2700
21
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
22
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
23
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
24
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
25
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
26