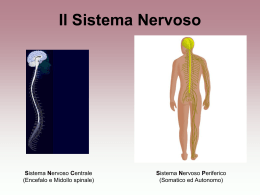
Attività cerebrale
•I neuroni si attivano in gruppi sotto l’azione di uno stimolo
•Attività in gruppi ben delimitati con alta o bassa attività
•Il gruppo di attività è chiamato “bolla”
•La bolla persiste a lungo e si restringe lentamente
Attività neuronale
In assenza di altri neuroni, l’attività del neurone j-esimo è:
d j
dt
   jii   n j 
n
i 1
Ove:
 j - attività del neurone j-esimo
 i - componente i-esima dello stimolo con “n” ingressi
 ji - peso della connessione tra neurone j-esimo e ingresso
i-esimo
 - perdite nel trasferimento delle informazioni
Equazione attività
L’andamento della sinapsi, in base alla distanza dal neurone, è:
 2G 

4 x y

e

1
2 
2
  

2
2
L’equazione dell’attività del neurone j-esimo diventa
d j
dt
   jii    j    wki k
n
i 1
k i
con wki = sinapsi connessione tra neurone “i” e “k”
x2  y2
2
Trasferimento informazioni
L’evoluzione temprale della sinapsi è espressa da
d ji
dt
 i i    j  ji
Con α che controlla la velocità di apprendimento
e β come fattore di dimenticanza
Dipende, quindi, dall’attività dei neuroni della connessione
L’attività varia in base alla posizione del neurone, dentro o
fuori dalla bolla
Neurone “entro”
•Attività massima, normalizzabile a 1
•Normalizzazione di α e β per avere  j ~   j 
d ji
dt
   i   ji 
La sinapsi cerca di uguagliare l’ingresso relativo
Neurone “fuori”
Attività trascurabile, ηj = 0
d ji
dt
0
Le sinapsi non vengono modificate
Reti di Kohonen
•Modello costruito nel 1983
•Rete auto-organizzante
•Replica il processo di formazione delle mappe cerebrali
•L’apprendimento si basa sulla competizione tra neuroni
Architettura
Griglia rettangolare di unità collegate a tutti gli ingressi
Unità lineare
x1
x2
xi
xn-1
xn
wj1
wj2
j
wji
wj(n-1)
wjn
n
y j   w ji x i
i 1
wji è il peso della connessione tra il neurone “j” e l’ingresso “i”
Neurone con uscita massima
n
y j   w ji x j  W j  X  W j X cos 
i 1
Necessaria la normalizzazione
X  W 1
Senza la normalizzazione
W1

W1 X cos   W2 X cos 
anche se
 

W2
X
Distanza vettore-ingresso
Viene scelto il neurone il cui vettore dei pesi è più vicino
all’ingresso
Non è necessaria la normalizzazione
Si può usare la distanza Euclidea
W1
d W j , X  
W2
X
 x  w 
N
i 1
2
i
ji
Legge di apprendimento
La legge di apprendimento per l’aggiornamento delle
sinapsi del neurone vincente risulta:


w ji k   w ji k  1   k  xi k   w ji k  1
j  V jo k 
con i  1,2...N
Vjo indica il vicinato del neurone vincente all’iterazione k
Dalla legge precedente, in notazione vettoriale:
W t     X  W 
Apprendimento cosciente
Adattamento alla distanza tra il neurone j-esimo ed il
neurone vincitore


w ji k   w ji k  1   k d  xi k   w ji k  1
j  V jo k 
con i  1,2...N
e d  DST  j, j0 
Scelte e variazioni
• Il vicinato va scelto in modo da imitare la biologia del
cervello
• La scelta del vicinato deve variare in modo da
includere tutti i neuroni
• Alla fine si dovrà avere il solo neurone vincente
Variazioni ed iterazioni
• Anche il fattore R varia
• Costante per un certo numero di iterazioni, poi
decresce
• Il numero delle iterazioni dell’algoritmo dipende dal
numero M di neuroni
• Solitamente (500÷5000)M
Riduzione di R e A
Rmax
r t 
Rmin
Amax
Amin
 Rmin
r t   Rmax 
 Rmax
t
Rmax
N

,
2
t
 Tmax


Rmin  1
t
 t 
t
 Amin  Tmax

 t   Amax 
 Amax 
Amax  1,
Amin  0
Algoritmo
1.
2.
3.
Inizializzazione casuale dei pesi
Inizializzazione parametri α=Amax e r=Rmax
Fino a che α>Amin
A. Per ogni ingresso,
i.
Calcolo dell’uscita
ii. Determinazione del neurone vincente
iii. Aggiornamento pesi del vicinato
B. Riduzione di “α” e “r”
Applicazioni
•Classificazione
•Es. odorato, fonemi
•Clustering
•Raggruppamento dati in sottoinsiemi di dimensione
limitata
•Compressione
•Es. immagini