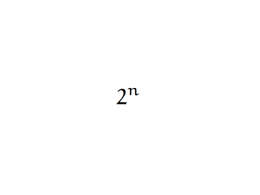Universita' di Ferrara
Facolta' di Scienze Matematiche, Fisiche e Naturali
Laurea Specialistica in Informatica
Algoritmi Avanzati
Programmazione strutturata
• sort per straight exchange o bubblesort
Copyright © 2006-2009 by Claudio Salati.
Lez. 4
1
Che fare?
•
Procedere in modo formale come si e' fatto nelle lezioni 2 e 3 e'
troppo pesante
•
Noi continueremo a dimostrare la correttezza e la terminazione
degli algoritmi che andremo ad esaminare, ma senza utilizzare
il formalismo della semantica assiomatica
•
Il quadro delle Premesse-Conseguenze restera' lo stesso, ma il
passaggio dalle une alle altre non sara' per operazioni formali
sul loro testo ma solo per ragionamento informale sulle (sulla
semantica intuitiva delle) istruzioni del nostro programma.
•
I nostri ragionamenti saranno basati su due metodi
fondamentali:
•
dimostrazione per assurdo
•
dimostrazione per induzione matematica
2
Il principio di induzione matematica
•
Consideriamo una asserzione P sull'intero n. Ad esempio:
 P (n) = "La somma dei primi n numeri dispari e' uguale a n2."
•
Si puo' dimostrare che P (n) e' vera per tutti gli interi positivi n nel
modo seguente:
•
si prova che P (1) e' vera (base dell'induzione)
•
si prova che, se sono vere P (1), P (2), …, P (n) per un
qualunque valore n, allora e' vera anche P (n+1)
(passo induttivo)
•
La stessa cosa si puo' fare ovviamente (in modo analogo) per
dimostrare P (n) per tutti gli interi non-negativi: basta considerare
come base P (0) anziche' P (1)
•
Per dare una dimostrazione per induzione matematica il primo
passo e' individuare su che cosa (su quale quantita') effettuare
l'induzione: e.g. il numero degli elementi di un vettore.
3
Il principio di induzione matematica
•
Completiamo l'esempio. Tesi: per ogni intero n1 vale P(n), dove:
 P(n) = "La somma dei primi n numeri dispari e' uguale a n2."
•
Dimostrazione:
– possiamo scrivere P(n) come:
n
2*k1
n

2
k
1
– Base dell'induzione: P(1) e' vera, infatti 1 = 12.
– Passo induttivo: Se P(k) e' vera per tutti i k da 1 a n, allora e'
vera in particolare per k=n, quindi possiamo assumere
(ipotesi induttiva) che P(n) sia vera.
Dimostriamo che di conseguenza P e' vera per n+1.
•
Sommiamo (2 * (n+1) - 1), cioe' (2 * n + 1) ai due lati di
P(n):
n1
2*k1
•
il lato sinistro diventa ovviamente
•
per il lato destro: n2 + 2 * n + 1 = (n + 1)2
k1
QED
4
Il principio di induzione matematica
Per effettuare una dimostrazione per induzione matematica occorre:
•
stabilire su quale quantita' si applica l'induzione:
la lunghezza della sequenza dei primi numeri dispari
•
esprimere il teorema nei termini della quantita' su cui si applica
l'induzione
P(n) = "La somma dei primi n numeri dispari e' uguale a n2."
•
stabilire per quale valore della quantita' su cui si applica l'induzione si ha
la condizione base dell'induzione
sequenza dei primi numeri dispari di lunghezza 1
•
dimostrare direttamente il teorema nella condizione base dell'induzione
•
esplicitare l'ipotesi induttiva e il passo induttivo
Se P(k) e' vera per tutti i k da 1 a n, allora e' vera in particolare per k=n,
quindi possiamo assumere (ipotesi induttiva) che P(n) sia vera.
Bisogna di conseguenza dimostrare la verita’ di P(n+1).
•
dimostrare il passo induttivo
N.B.: quando si invoca l'ipotesi induttiva bisogna fare vedere che essa e'
5
applicabile.
Principio di induzione matematica: esempio 2
•
Consideriamo la seguente funzione:
unsigned fattoriale(unsigned int n) {
// NB: unsigned int  n0
return (n==0 ? 1 : (n * fattoriale(n-1));
}
•
Tesi: essa calcola correttamente la funzione n!.
(nell'ipotesi di ignorare i vincoli di architettura (sizeof(unsigned)))
•
Dimostrazione (per induzione matematica):
• Base dell'induzione: se n=0 la funzione ritorna 1, cioe' 0!.
• Passo induttivo: consideriamo un qualunque valore n>0.
• Poiche' n0 la funzione ritorna n*fattoriale(n-1)
• Per ipotesi induttiva fattoriale(n-1) = (n-1)!
• Quindi la funzione ritorna n * (n-1)! = n!
QED
6
Principio di induzione matematica: esempio 2
•
su quale quantita' si applica l'induzione?
Il valore dell'intero passato come parametro di ingresso alla funzione
•
il teorema nei termini della quantita' su cui si applica l'induzione:
fattoriale(unsigned n) calcola correttamente n! per
qualunque valore k0 in ingresso
•
per quale valore della quantita' su cui si applica l'induzione si ha la
condizione base dell'induzione?
n=0
•
dimostrare direttamente il teorema nella condizione base
dell'induzione
N.B.: La dimostrazione deve fare riferimento al testo della funzione.
Se n=0 la condizione di controllo dell'operatore triadico ?: e' vera, per
cui il risultato dell'espressione e' il valore del secondo operando
dell'operatore.
7
Continua alla pagina seguente
Principio di induzione matematica: esempio 2
•
ipotesi induttiva e passo induttivo
fattoriale(unsigned n) calcola correttamente n! quando il
parametro di ingresso ha valore <k.
Il passo induttivo dimostra che fattoriale(unsigned n) calcola
correttamente n! quando il parametro di ingresso ha valore =k, con
k>0 (il caso base e' gia' dimostrato).
•
dimostrare il passo induttivo
N.B.: la dimostrazione deve fare riferimento al testo della funzione.
Quando si invoca l'ipotesi induttiva (chiamata ricorsiva) occorre fare
vedere
• che essa e' applicabile (nel nostro caso, che il parametro di
ingresso passatole rientra tra i valori coperti dall'ipotesi induttiva,
cioe' e' <k)
• che la chiamata ricorsiva soddisfa le precondizioni imposte dalla
funzione (in particolare, che il parametro di ingresso e' 0, il che
8
e' garantito essendo =k-1 con k>0 ).
Principio di induzione matematica: esercizi
•
Dimostrare tramite l'applicazione del principio di induzione
matematica la validita' delle seguenti formule:
n*(n
1
)
k

2
k
1
n
n

1
1

x
a
*
x
a
*

1

x
k

0
n
•
k
Dimostrare tramite l'applicazione del principio di induzione
matematica la correttezza dell’a”algoritmo del torneo” per
l’identificazione dell’elemento minimo di un vettore.
9
Ordinamento di un vettore
•
Dato un vettore di N elementi interi, N1, ordinarlo in modo non
decrescente
•
Premessa:
P = { N1, int v[N] }
•
Conseguenza:
C = { N1, int v[N], j=0..N-2 : v[j]  v[j+1] }
•
La premessa dichiara l'esistenza di un vettore v formato da N
elementi interi, con N 1.
•
La conseguenza dichiara che ogni elemento di v (che abbia un
elemento successivo) e' minore o uguale dell'elemento
successivo.
•
N.B.: si e' omesso di specificare che il vettore di uscita deve
essere una permutazione di quello di ingresso
10
Sort di un vettore, strategia straight-exchange
•
Strategia:
• ALL’i-ESIMA ITERAZIONE IL SOTTOVETTORE v[0]..v[i-2] E'
GIA' ORDINATO (globalmente, rispetto all’intero v)
• SI ANALIZZANO GLI ELEMENTI DEL SOTTOVETTORE
v[i-1]..v[N-1]
• PARTENDO DAL FONDO, SI SCANDISCE UNO PER UNO
CIASCUN ELEMENTO DEL SOTTOVETTORE E LO SI
CONFRONTA CON QUELLO PRECEDENTE
• SI SCAMBIANO TRA LORO GLI ELEMENTI ADIACENTI TALI
CHE v[k]<v[k-1], con ikN-1
• COSI' ALL'i-ESIMA ITERAZIONE VIENE SISTEMATO
DEFINITIVAMENTE L’ELEMENTO DI INDICE i-1
(attraverso una sequenza di scambi con elementi adiacenti)
11
STRAIGHT EXCHANGE o BUBBLESORT
• Perche’ bubblesort?
• Perche’ gli elementi piu’ piccoli risalgono ad ogni iterazione
dal fondo del vettore verso l’inizio del vettore;
• in particolare, l’elemento piu’ piccolo della parte di vettore non
ancora ordinata emerge fino a raggiungere la sua posizione
definitiva nel vettore ordinato,
• quindi, la posizione immediatamente successiva all’ultima del
sottovettore gia’ ordinato in precedenza.
• All’i-esima iterazione si fa emergere fino alla posizione i-1
l’elemento che deve occupare quella posizione nel vettore
ordinato.
• N.B.: la risalita e' fino alla posizione i-1 perche' il sottovettore
v[0..i-2] e' gia' ordinato e i suoi elementi sono tutti  degli
elementi del sottovettore v[i-1..N-1]
• Un valore risale dal fondo lungo il vettore fino a che incontra
un elemento minore o uguale a lui: a quel punto si ferma ed e'
12
questo secondo valore che inizia una analoga risalita.
Bubblesort: la strategia
L'algoritmo
•
L3-annex.doc fornisce la descrizione del progetto formale (con il
metodo top-down e la pratica delle asserzioni) dell'algoritmo
•
Qui ne vediamo la versione informale;
• La strategia ci dice che la funzione bubbleSort() e'
organizzata come una coppia di cicli innestati tra loro
• Il ciclo esterno serve a estendere la parte (il prefisso) del
vettore gia' ordinata
• Il ciclo interno serve a fare emergere nella cella del vettore
immediatamente successiva alla parte gia' ordinata
l'elemento minimo della parte di vettore ancora non
ordinata
13
Bubblesort: l'algoritmo
•
Situazione all'i-esima iterazione del ciclo esterno:
vettore v
v[0] .. v[i-2] ordinato
v[i-1]
v[i]
...
v[N-1]
i
v[0]..v[i-2] tratto del vettore gia' globalmente (quindi
definitivamente) ordinato in modo non
decrescente.
Non solo gli elementi del sottovettore v[0]..v[i-2]
sono ordinati tra loro: ciascuno di essi e'  di tutti
gli elementi del sottovettore v[i-1]..v[N-1]
i-1
indice della posizione del vettore per la quale
voglio far emergere l'elemento minimo all'interno
del sottovettore non-ordinato v[i-1]..v[N-1]
14
Bubblesort: l'algoritmo
•
Quando termina il ciclo esterno?
vettore v
v[0] .. v[N-2] ordinato
v[N-1]
i=N
•
Occorre che il vettore sia completamente ordinato.
•
Il che avviene quando tutti gli elementi del sottovettore
v[0]..v[N-2] sono globalmente ordinati.
•
Cioe' quando i = (N-2)+2 = N.
•
N.B.: poiche' l'elemento v[N-1] e' maggiore o uguale di tutti
gli elementi del sottovettore v[0]..v[N-2] si ha che l'intero
vettore v[0]..v[N-1] e' ordinato.
15
Bubblesort: l'algoritmo
•
Situazione alla k-esima iterazione del ciclo interno:
vettore v v[0] .. v[i-2] ordinato
v[i-1] ...
v[scan]
... v[N-1]
scan
v[0]..v[i-2] tratto del vettore gia' globalmente (quindi
definitivamente) ) ordinato in modo non
decrescente.
i-1
indice della posizione del vettore per la quale
voglio far emergere l'elemento minimo all'interno
del sottovettore non-ordinato v[i-1]..v[N-1]
scan
indice della posizione fino alla quale ho gia'
processato (dal fondo) il sottovettore non ordinato
v[i-1]..v[N-1], facendo emergere nella posizione
scan l'elemento minimo del suffisso v[scan]..v[N-1]
16
Bubblesort: l'algoritmo
•
Quando termina il ciclo interno?
vettore v v[0] .. v[i-2] ordinato
v[i-1] ...
v[scan]
... v[N-1]
scan
•
Quando in v[i-1] e' emerso l'elemento minimo del
sottovettore (non ordinato) v[i-1]..v[N-1].
•
Quindi quando e': scan = i-1
17
Bubblesort: l'algoritmo
•
Dalla descrizione della strategia discendono:
• la seguente scomposizione del programma
• gli invarianti P1 e P2
• le condizioni di controllo dei due cicli innestati
void bubbleSort(int N, int v[]) {
1
S0;
2
// P1= {P; iN; (j: 0<ji-2) v[j-1]v[j];
//
(j, k: 0ji-2, i-1kN-1) v[j]v[k]}
while (i <= N-1) {
3
S1;
4
// P2={P1; i<=N-1; (i-1)scanN-1;
//
(j: scanjN-1) v[scan]v[j] }
while (scan >= i) {
5
S2;
6
} // end while
7
i += 1;
8
} // end while
9
18
}
10
Bubblesort: l'algoritmo
void bubbleSort(int N, int v[]) {
int i = 1;
// P1= {P; iN; (j: 0<ji-2) v[j-1]v[j];
//
(j, k: 0ji-2, i-1kN-1) v[j]v[k]}
while (i <= N-1) {
int scan = N-1;
// P2={P1; i<=N-1; (i-1)scanN-1;
//
(j: scanjN-1) v[scan]v[j] }
while (scan >= i) {
if (v[scan-1]>v[scan]) {
int x = v[scan-1];
v[scan-1] = v[scan];
v[scan] = x;
} // end if
scan -= 1;
} // end while
i += 1;
} // end while
}
1
2
3
4
5
6
7
8
9
10
11
12
13
19 14
Bubblesort: correttezza
Correttezza
• Lemma: il ciclo interno fa emergere l'elemento minimo del
sottovettore v[i-1]..v[N-1] nella posizione i-1
• Dimostrazione: per induzione matematica sul numero di cicli e
quindi sul valore di scan
• Base dell'induzione: prima di entrare nel ciclo (riga 4) la prima
volta scan  N-1, ed e' quindi banalmente vero che
(j: scanjN-1) v[scan]v[j]
• Assumiamo per ipotesi induttiva che la proprieta' valga all'inizio
di una qualunque iterazione:
• durante questa, se v[scan-1]>v[scan] i due elementi
vengono scambiati (righe 6-8);
• in ogni caso, dopo l'istruzione if (riga 10) :
v[scan-1]v[scan] e quindi anche, per ipotesi induttiva,
(j: scanjN-1) v[scan-1]v[j]
• l'invariante e' ripristinato decrementando scan. QED
20
Bubblesort: correttezza
Lemma, Dimostrazione per induzione matematica:
•
su quale quantita' si applica l'induzione?
sulla lunghezza del sottovettore finale di cui v[scan] e' l'elemento
minimo (data da N-1-scan)
•
il teorema nei termini della quantita' su cui si applica l'induzione:
P(N-1-scan) = v[scan] e' l'elemento minimo del sottovettore
v[scan..N-1]
•
per quale valore di N-1-scan si ha la condizione base dell'induzione?
N-1-scan=0, cioe' per un sottovettore di lunghezza 1
•
dimostrare direttamente il teorema nella condizione base dell'induzione
v[N-1] e' l'elemento minimo del sottovettore v[N-1..N-1]
•
esplicitare l'ipotesi induttiva e il passo induttivo
ipotesi induttiva: (j: scanjN-1) v[scan]v[j]
passo induttivo: (j: scan-1jN-1) v[scan-1]v[j]
con scani
•
dimostrare il passo induttivo
21
Bubblesort: correttezza
Correttezza
• nel momento in cui il ciclo interno termina e': scan=i-1
• e in v[i-1] (cioe' in v[scan]) c'e' l'elemento minimo del
sottovettore v[i-1..N-1]
• cioe'
(j: i-1jN-1) v[i-1]v[j]
• che e' la proprieta' che deve essere garantita dall'esecuzione del
ciclo interno
22
Principio di induzione matematica e iterazione
• Riscriviamo in modo ricorsivo la procedura di emersione:
void bubbleUp (int v[], int low,
int high, int scan) {
// pre.1 = (j: scanjhigh) v[scan]v[j]
// pre.2 = low  scan  high
if (scan>low) {
if (v[scan] < v[scan-1]) {
int x = v[scan-1];
v[scan-1] = v[scan];
v[scan] = x;
} // end if
// (j: scan-1jhigh) v[scan-1]v[j]
bubbleUp (v, low, high, scan-1);
}
// (j: lowjhigh) v[low]v[j]
return;
}
1
2
3
4
5
6
7
8
9
10
11 23
bubbleUp()
• Situazione con low<scan<high:
vettore v
...
...
low
...
scan
...
high
v[0..low-1]
tratti del vettore irrilevanti
v[high+1..N-1]
low
indice della posizione del vettore per la quale
voglio far emergere l'elemento minimo
all'interno del sottovettore non-ordinato
v[low..high]
scan
al momento della attivazione di bubbleUp() e'
garantito dalla precondizione pre.1 che v[scan]
e' l'elemento minimo del sottovettore nonordinato v[scan..high]
24
Correttezza di bubbleUp()
•
Lo scopo di bubbleUp() e' di fare emergere in low l'elemento
minimo del sottovettore v[low..high]
•
In particolare quello che si vuole (ad esempio nel caso della
funzione cliente bubbleSort()) e' che la chiamata
bubbleUp(v, low, high, high);
effettuata senza alcuna precondizione (eccetto pre.2) sul
sottovettore v[low..high], faccia emergere in low l'elemento
minimo del sottovettore.
•
In realta', quando scan=high, entrambe le precondizioni di
bubbleUp() sono verificate (la prima in modo banale).
•
Quindi possiamo riformulare la nostra tesi come:
bubbleUp(), quando chiamata correttamente (con le sue
precondizioni verificate), opera correttamente (per tutti i valori
legali di scan, cioe' per scan=low..high)
25
Correttezza di bubbleUp()
Dimostrazione di correttezza per induzione di bubbleUp() - parte 1
•
su quale quantita' si applica l'induzione?
sulla lunghezza del sottovettore v[low]..v[scan]
•
il teorema nei termini della quantita' su cui si applica l'induzione:
bubbleUp() posiziona in v[low] l'elemento minimo del sottovettore
v[low]..v[high], per qualunque valore di scan nel range
low..high purche' sia chiamata con soddisfatta precondizione pre.1
•
per quale valore di scan si ha la condizione base dell'induzione?
scan==low
•
dimostrare direttamente il teorema nella condizione base dell'induzione
immediata dalla precondizione pre.1: in questo caso la funzione non fa (e
non deve fare) niente!
vettore v
...
...
low=scan
...
high
26
Correttezza di bubbleUp()
Dimostrazione di correttezza per induzione di bubbleUp() - parte 2
•
esplicitare l'ipotesi induttiva e il passo induttivo
ipotesi induttiva: bubbleUp (v, low, high, scan), essendo
soddisfatta la precondizione pre.1, opera correttamente per ogni valore k
di scan tale che sia lowkmhigh
passo induttivo: bubbleUp (v, low, high, scan), essendo
soddisfatta la precondizione pre.1, opera correttamente per il valore di
scan m+1, con m+1 high (per cui in questa condizione e' scan>low)
•
dimostrare il passo induttivo
• In questo caso il corpo dell'if di riga 2 viene eseguito
• dopo l'esecuzione dell'if di riga 3, in ogni caso, v[scan-1] e' minore
di tutti gli elementi successivi del vettore
• la chiamata ricorsiva di riga 8
• soddisfa tutte le precondizioni della funzione e
• si applica su un sottovettore di lunghezza strettamente minore,
per cui risulta applicabile l'ipotesi induttiva
27
Principio di induzione matematica e iterazione
•
Le due versioni, iterativa e ricorsiva, della procedura di emersione
sono evidentemente correlate tra loro
•
Anche le loro dimostrazioni per induzione matematica lo sono!
 anche se operano in modo speculare
•
In realta' un ciclo rappresenta una dimostrazione costruttiva del
principio di induzione matematica
•
Quando parliamo di induzione matematica su un ciclo ci riferiamo
in realta' alla dimostrazione che il ciclo mantiene il proprio
invariante
Analogie tra struttura del ciclo e dimostrazione per induzione
inizializzazione del ciclo

condizione base dell'induzione
invariante del ciclo

ipotesi induttiva
iterazione

passo induttivo
terminazione

condizione base dell'induzione
28
Bubblesort: correttezza
Correttezza
•
bubbleSort() ordina il vettore in input in modo non
decrescente
•
Dimostrazione: per induzione matematica sul numero di cicli e
quindi sul valore di i
• Base dell'induzione: prima di entrare nel ciclo la prima volta i
vale 1, ed e' quindi banalmente vero che
(j: 0<ji-2) v[j-1]v[j];
(j, k: 0ji-2, i-1kN-1) v[j]v[k]
• Assumiamo per ipotesi induttiva che la proprieta' valga anche
all'inizio di una qualunque iterazione
• Durante l'iterazione, alla fine del ciclo while interno, per il
lemma vale anche (j: ijN-1) v[i-1]v[j], e
quindi
(j: 0<ji-1) v[j-1]v[j];
(j, k: 0ji-1, ikN-1) v[j]v[k]
• l'invariante e' ripristinato incrementando i.
29
Bubblesort: correttezza
Correttezza
•
Al momento della terminazione del ciclo e':
i==N
•
Unitamente all'invariante questo garantisce che sia
(j: 0<jN-2) v[j-1]v[j];
(j, k: 0jN-2, N-1kN-1) v[j]v[k]
•
E quindi
(j: 0<jN-1) v[j-1]v[j];
•
Per cui il vettore v[] e' completamente ordinato. QED
30
Bubblesort: terminazione
Terminazione dell'algoritmo
•
LA TERMINAZIONE DELL'ALGORITMO E' GARANTITA
PERCHE':
• E' GARANTITA LA TERMINAZIONE DEL CICLO
INTERNO: scan decresce ad ogni iterazione e i rimane
fisso
• E' GARANTITA LA TERMINAZIONE DEL CICLO
ESTERNO POICHE'
• N E' COSTANTE
• i E' MONOTONA CRESCENTE AD OGNI
ITERAZIONE
•
E QUINDI LA CONDIZIONE DI CIASCUN WHILE SARA'
NECESSARIAMENTE FALSIFICATA
(in particolare, per il ciclo esterno, dopo N-1 iterazioni)
31
Bubblesort: complessita'
Complessita' dell'algoritmo
•
Quanti passi (confronti) richiede l'algoritmo?
• N-1 confronti (all'interno del ciclo interno) durante la prima
iterazione del ciclo esterno (e possibilmente anche N-1
scambi, ciascuno dei quali costa 3 assegnamenti);
• N-2 confronti (e possibilmente scambi) durante la seconda
iterazione del ciclo esterno;
• e cosi' via …
•
cioe', un totale di operazioni pari a
N




4
*
N

i
2
*
N

1
*
N

i

1
•
quindi l'algoritmo e' di complessita' O(n2)
32
Bubblesort: esercizio
•
Avremmo potuto riformulare la strategia dell'algoritmo di
bubblesort nel modo seguente:
• v[0]..v[i-1] : tratto del vettore gia' globalmente (quindi
definitivamente) ordinato in modo non decrescente.
Non solo gli elementi del sottovettore v[0]..v[i-1] sono
ordinati tra loro: ciascuno di essi e'  di tutti gli elementi del
sottovettore v[i]..v[N-1]
• i : indice della posizione del vettore per la quale voglio far
emergere l'elemento minimo all'interno del sottovettore nonordinato v[i]..v[N-1]
•
Riscrivere la funzione bubblesort() e i relativi invarianti
secondo questa riformulazione.
33
Bubblesort: versione volgare
 Esiste anche una versione "volgare" di bubblesort:
void dummyBubbleSort(int N, int v[]) {
int thereWasAnExchange = 1;
// = true
while ( thereWasAnExchange ) {
thereWasAnExchange = 0;
// = false
int scan = N-1;
while (scan >= 1) {
if (v[scan-1]>v[scan]) {
thereWasAnExchange = 1; // = true
int x = v[scan-1];
v[scan-1] = v[scan];
v[scan] = x;
} // end if
scan -= 1;
} // end while
} // end while
}
34
Bubblesort: versione volgare
•
Questa versione di bubblesort ne nasconde la logica vera
•
la sua strategia apparente e':
fino a che il vettore non e' ordinato (cioe' fino a che c'e' almeno
una coppia di elementi adiacenti che non rispetta la relazione
d'ordine) lo scandisco tutto, scambiando tra loro ciascun
elemento e il suo adiacente se non e' rispettata la relazione
d'ordine
•
la condizione di terminazione del ciclo e': la relazione d'ordine e'
rispettata per tutte le coppie di elementi adiacenti (e di
conseguenza il vettore e' ordinato).
•
Questa condizione e' rilevata perche' si e' fatta un'intera passata
sul vettore senza effettuare alcuno scambio:
 quindi non c'era nessun elemento non ordinato rispetto agli
elementi adiacenti
•
c'e' del buono in questa strategia?
35
Bubblesort: versione volgare
•
Poiche' ogni iterazione del ciclo interno di bubbleSort(),
oltre che fare emergere l'elemento minimo del sottovettore
ancora da ordinare, fa anche risalire verso la superficie altri
elementi, puo' succedere che il vettore risulti ordinato anche
prima della terminazione del ciclo esterno
•
Esercizio: modificare bubbleSort() integrandolo con la
logica di dummyBubbleSort() per accelerarne la
terminazione
36