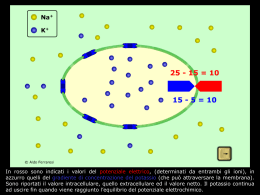
CHI GENERA IL POTENZIALE DI
MEMBRANA?
In una cellula permeabile ad un solo ione: il
potenziale di membrana coincide con il potenziale
di equilibrio elettrochimico dello ione
Potenziali di membrana
1
IL POTENZIALE ELETTROCHIMICO
membrana selettiva ad un solo ione
flusso netto di K+ nullo
∆V = 0
flusso netto di K+ da I a II
equilibrio tra gradiente
elettrico e chimico
∆V ≠ 0
Il potenziale elettrochimico di uno ione deriva da:
- il gradiente ionico tra i compartimenti intracellulare
ed extracellulare
Potenziali di membrana
2
- la permeabilità selettiva della membrana
L’equazione di Nernst per calcolare
il potenziale di equilibrio di uno ione
Il potenziale elettrochimico (µ) di uno ione (x) è definito
come:
µx = RT ln[x] + zFEx
R = costante dei gas = 8.315 (J K-1 mol -1)
F = costante di Faraday = 9.649 x 104 (C mol -1)
z = valenza
T = temperatura assoluta
E = potenziale elettrico
La differenza di potenziale elettrochimico dello ione attraverso la
membrana è:
∆µx = µI(x) - µII(x) = RT ln[x]I/[x]II + zF(EI- EII)
in condizioni di equilibrio:
∆µx = 0
da cui :
EI- EII = RT/zF ln[x]II/[x]I
Potenziali di membrana
3
Nel caso di una membrana cellulare, per convenzione si assume
EII = 0 (lato extracellulare), quindi:
Ex= RT/zF ln[x]II/[x]I
(equazione di Nernst)
ad una temperatura di 20° C, con z = +1 il rapporto RT/zF vale
25.2 mV e ricordando che:
ln x = 2.303 log x
possiamo riscrivere l’equazione di Nernst come:
Ex = 58 mV log[x]II/[x]I
Esempio:
Consideriamo una membrana come nell’esempio precedente,
permeabile unicamente al K+, in cui [K]i = 10 [K]o.
In queste condizioni:
EK = 58 mV log[K]o/[K]i
= 58 mV log 0.01/0.1 = 58 mV log 1/10
= - 58 mV
(è negativo!!!)
Regola:
La differenza di potenziale aumenta di un fattore 58 mV quando
la differenza di concentrazione
ione permeante aumenta4 di
Potenziali didello
membrana
10 volte.
Dipendenza di EK dal K+ extracellulare
- se una membrana è
permeabile ad una sola
specie ionica, ad
esempio K+:
Vm = EK
- la membrana si
comporta come un
elettrodo al K+
Circuito equivalente di una membrana cellulare
permeabile solo al K+
IK = gK (E-EK)
Potenziali di membrana
5
Potenziali di equilibrio di altri ioni permeanti
ENa= RT/zF ln [Na]o/[Na]i
ECa= RT/zF ln [Ca]o/[Ca]i
ECl= RT/zF ln [Cl]i/[Cl]o
nel caso di concentrazioni intra- ed extracellulari di una
cellula muscolare scheletrica di rana:
ione
intracellulare (mM)
extracellulare (mM)
Na+
12
145
K+
155
4
Ca2+
10-7 (M)
1.5
Cl -
4.2
123
si ottengono i seguenti valori dei potenziali di equilibrio:
ENa= +67 mV
EK= -98 mV
ECa= +129 mV
ECl= -90 mV
Potenziali di membrana
6
Dipendenza del potenziale di membrana
dal K+ extracellulare
• Il potenziale di riposo della membrana segue la legge di
Nernst per [K+]o > 5 mM.
• Quando [K+]o < 5 mM i punti sperimentali differiscono dalla
retta e seguono l’equazione di Goldman.
Potenziali di membrana
7
COME SI CALCOLA Vm NEL CASO DI UNA
CELLULA PERMEABILE A 3 SPECIE
IONICHE?
Il potenziale di membrana è la media “pesata”
dei potenziali elettrochimici dei singoli ioni
permeanti
Potenziali di membrana
8
Equazione di Goldman-Hodgkin-Katz
ƒ Membrana permeabile a tre specie ioniche: Na+, K+, Cl–
ƒ Ciascuno ione ha un suo coefficiente di permeabilità Px
ƒ Vm si calcola secondo la seguente equazione:
PK[K+]e + PNa[Na+]e + PCl[Cl-]i
RT
ln
Vm =
F
PK[K+]i + PNa[Na+]i + PCl[Cl-]e
Esempio di applicazione dell’equazione di GHK:
PCl = 0
PNa / PK = 0.01
1[K+]e + 0.01[Na+]e
RT
ln
Vm =
F
1[K+]i + 0.01[Na+]i
sostituendo:
[K+]e = 2.5 mM
[Na+]e = 120 mM
[K+]i = 140 mM
[Na+]i = 10 mM
Vm = 58 mV log
2.5 + 0.01 x 120
= -92 mV
140 + 0.01 x 10
Nota: Nelle condizioni ioniche dell’esempio, i potenziali
di equilibrio calcolati
con l’eq.
di Nernst valgono: ENa =
Potenziali
di membrana
+63 mV e EK = -102 mV
9
Riepilogo:
IL POTENZIALE DI MEMBRANA A RIPOSO
ƒ
Il potenziale di riposo della membrana varia tra –50 e –90 mV
ed è determinato da:
1) Canali ionici aperti e selettivamente permeabili ad uno ione
2) Gradiente ionico mantenuto stabilmente da trasporti attivi
ƒ
Gli ioni influenzano il potenziale di membrana in base alla
loro permeabilità relativa (equazione di Goldman)
ƒ
Il potenziale di riposo delle cellule eccitabili è più sensibile
alle variazioni di K+ rispetto agli altri ioni. Questo è dovuto
alla maggior permeabilità al K+ a riposo
ƒ
Il potenziale di riposo negativo è dovuto all’alta
concentrazione di K+ intracellulare e alla tendenza dello ione
a uscire dalla cellula, scoprendo una carica netta negativa
attraverso i pochi canali del K+ aperti a riposo.
ƒ
Gli ioni Na+ contribuiscono poco al potenziale di riposo in
quanto la membrana (a riposo) è poco permeabile ad essi.
Bassissima probabilità di apertura al di sotto di –40 mV.
ƒ
A seconda del tipo di cellule il Cl– (attraverso i canali del Cl–
di “leakage”) può contribuire in diversa misura al
mantenimento del potenziale di riposo.
ƒ
Il trasporto attivo mantiene i gradienti ionici
Potenziali di membrana
10
COSA SUCCEDE AD UNA CELLULA IN CUI
LE CONDUTTANZE AL Na+ E AL K+
CAMBIANO NEL TEMPO?
Potenziali di membrana
11
Segnali elettrici di membrana generati
da variazioni di conduttanze ioniche
1o Esempio: consideriamo una membrana permeabile al K+ a
riposo che diventa permeabile anche al Na+ durante un breve
intervallo
A riposo, quando gK = 100 gNa
Vm = –92 mV
Durante la variazione di conduttanza,
quando gNa = gK
Potenziali di membrana
–5.1 mV (calcolato con l’eq. di Goldman)
V12m =
2o Esempio: consideriamo una membrana parzialmente permeabile
al K+ e poco al Na+ a riposo che diventa prima
molto permeabile al Na+ (per un breve intervallo) e poi
molto permeabile al K+ (per un intervallo più lungo)
Potenziali di membrana
13
COME SI GENERANO I SEGNALI ELETTRICI
IN UNA CELLULA ECCITABILE?
Potenziali di membrana
14
PROPRIETÀ ELETTRICHE ATTIVE E PASSIVE
DELLA MEMBRANA CELLULARE
Se iniettiamo corrente (Im) in un neurone per far variare Vm,
cosa succede?
Potenziale di membrana (mV)
Tracce 1-2:
iperpolarizzazione
(rimuovo cariche + dal
citoplasma, risposta
passiva)
potenziale di soglia
Stimolo di corrente (nA)
Traccia 3:
depolarizzazione
(fornisco cariche + al
citoplasma, risposta
passiva)
Traccia 4:
lo stimolo è sufficiente
ad innescare una
risposta attiva:
potenziale d’azione
Im
Vm
Im
cellula
Potenziali di membrana
15