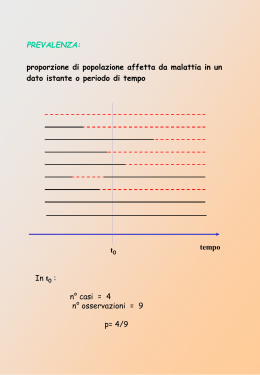
Semeiotica & Metodologia Clinica
Aspetti metodologici dell’utilizzazione
ed interpretazione dei tests di
laboratorio e strumentali
Enrico Fiaccadori
09.11.2004
Scopi dei tests medici
(esami di laboratorio o strumentali)
•
•
•
•
Fare una diagnosi
Effettuare uno screening
Definire una prognosi
Monitorare una terapia
La diagnosi: un processo cognitivo
La diagnosi è un processo cognitivo
complesso basato sul ragionamento logico
ed il riconoscimento di patterns di malattia
Il ragionamento logico che porta alla diagnosi
inizia da un problema clinico, che di solito
rappresenta l’oggetto della diagnosi differenziale
Problema clinico
• Reperto anamnestico (sintomi o segni, ad es. dolore toracico o
insorgenza di edema agli arti inferiori)
• Reperto obiettivo (sintomi o segni, ad dispnea o cianosi)
• Reperto strumentale (ad es. opacità polmonare all’Rx torace)
• Reperto di laboratorio (ad es. anemia)
Se i problemi clinici sono più di uno, va individuato il più urgente e/o
quell’insieme di problemi clinici che consentono di individuare una o
più ipotesi di lavoro plausibili (working hypothesis o leading
hypothesis) sulla base delle diagnosi possibili.
Per working hypothesis si intende quindi la diagnosi che al momento
fornisce la spiegazione più plausibile dei problemi clinici del paziente
L’approccio al paziente va imparato studiandolo
prevalentemente per problemi clinici
(e non solo per patologie)
- Libri di testo basati sull’integrazione tra casi
clinici e discussione di strategie diagnostiche
- Discussione di casi clinici in Reparto
Quando si ragiona in termini di diagnosi differenziale,
come si decide da quale ipotesi cominciare?
1) Criterio possibilistico: tutte le ipotesi diagnostiche vengono
considerate alla stessa stregua  si testano tutte (il paziente
viene sottoposto a numerosi esami spesso inutili, a volte
pericolosi, ed i costi aumentano)
2) Criterio selettivo: il medico sceglie in base alla probabilità
(approccio probabilistico), e/o in base alla eventuale pericolosità
di una diagnosi non fatta o non esclusa (approccio prognostico)
e/o in base all’eventuale possibilità di risposta al trattamento
(approccio pragmatico). Tutti i criteri selettivi sono corretti, e di
solito vengono utilizzati contemporaneamente per stabilire la
working hypothesis.
Il ragionamento diagnostico: due tappe fondamentali
• Nella prima vengono enumerate le possibilità diagnostiche a
partenza dal problema clinico, o da un insieme di problemi clinici
(cluster), che a volte possono configurare una vera e propria
sindrome; le relative probabilità sono confrontate  se possibile,
si individua la (o lle) working hypothesis
• Nella seconda tappa vengono incorporate nuove informazioni, allo
scopo di modificare la verosimiglianza delle ipotesi diagnostiche,
nel senso di eliminare le ipotesi diagnostiche con caratteristiche di
minor probabilità e di scegliere quelle più probabili, oppure di
confermare in maniera definitiva la working hypothesis
I test diagnostici di laboratorio rappresentano un potente
mezzo per modificare (aumentandola o riducendola) la
verosimiglianza di una ipotesi diagnostica
Dal problema clinico alla diagnosi di malattia (1)
Partendo da un problema clinico e ragionando in maniera probabilistica
sulle possibilità di diagnosi differenziale, il medico cerca di comporre un
insieme di reperti (anamnestici, obiettivi, strumentali e di laboratorio)
che individuano una o più working hypothesis. Ad es.:
- paziente di sesso femminile di 49 anni, fumatrice, riferisce dispnea
insorta acutamente + dolore all’emitorace dx, di tipo puntorio, comparso
improvvisamente a riposo, da circa 2 ore, che si aggrava con la
respirazione profonda + tosse secca + temperatura 37.8°
Dal problema clinico alla diagnosi di malattia (2)
Cluster di problemi clinici: dispnea acuta associata a febbre
e dolore toracico trafittivo in giovane donna
Ipotesi diagnostiche possibili (le più probabili):
a) embolia polmonare
b) pnx spontaneo
c) pleurite
d) polmonite
 Working hypothesis: embolia polmonare
All’E.O: non reperti patologici
Tests diagnostici eseguiti:
Emogasanalisi arteriosa: PaO2 50 mmHg, PaCO2 30 mmHg
Rx torace: non focolai di addensamento polmonare, non segni di pnx
Scintigrafia polmonare di flusso  difetti multipli bilaterali
vascolarizzazione polmonare
-> Diagnosi: embolia polmonare
di
Dopo l’individuazione della (o delle) working hypothesis
avviene la fase di consolidamento del processo diagnostico
(conferma o esclusione dell’ipotesi di lavoro), che di solito si
basa sui tests diagnostici
Sulla base di ciascuna nuova informazione (tests diagnostici) il clinico si muove,
spesso in maniera intuitiva ed implicita, da una probabilità iniziale di diagnosi
(probabilità pre-test), ad un’altra probabilità di diagnosi (probabilità posttest), in base alla quale confermiamo o escludiamo lipotesi di lavoro)
Rispetto alla probabilità pre-test, la probabilità post-test potrà essere
notevolmente aumentata ( la diagnosi è confermata) o notevolmente diminuita
(la diagnosi è esclusa), a seconda del risultato del test diagnostico (posit o negat).
Se conosciamo le proprietà di ciascuna informazione (caratteristiche operative del
test diagnostico) possiamo quantificare con esattezza l’entità dell’effetto di un
test suI processo diagnostico, e cioè l’impatto del test sulla probabilità iniziale di
una determinata diagnosi.
In altre parole potremo quantificare con precisione l’utilità di un test, cioè quanto
il test ha modificato in un senso o nell’altro il nostro modo di pensare (probablità
post-test) su di una possibile diagnosi, rispetto all’idea iniziale che ci eravamo
fatti (probabilità post-test) in base alla nostra esperienza o alla letteratura
scientifica.
Probabilità pre-test
Quale è la probabilità
di quella diagnosi in
una coorte di 100
pazienti sovrapponibili
a quello che sto
valutando?
Prevalenza
della malattia

Caratteristiche
operative del test
Il test che voglio
eseguire è in grado di
aumentare o ridurre la
probabilità pre-test
della malattia, e di
quanto?
 Performance
del test
Probabilità post-test
paziente di sesso femminile di 49 anni, fumatrice, riferisce dispnea
insorta acutamente e dolore all’emitorace dx, di tipo puntorio, comparso
improvvisamente a riposo, da circa 2 ore, che si aggrava con la
respirazione profonda ed è associato a tosse secca; temperatura 37.8°
Working hypothesis: embolia polmonare
Qual è la probabilità pre-test (cioè la prevalenza) di embolia polmonare in pazienti
sovrapponibili (età, sesso, fattori di rischio, presentazione clinica etc.)?
 il 28% dei pazienti con dolore toracico di tipo pleuritico ed età superiore a 40
anni ha embolia polmonare (Hull RD et a., Pulmonary embolism in outpatients with
pleuritic chest pain. Arch Int Med 1988; 148:838-844)
Il 65% dei pazienti ha una polmonite
Eseguendo una scintigrafia polmonare la probabilità di embolia polmonare, se
l’esame è positivo, passa dal 28% all’82%  la diagnosi è confermata e la
paziente va trattata.
Eseguendo una angiografia polmonare la probabilità passa dall 28% al 99%
Entrambi i test hanno una buona performance e sono utili: scelgo di fare il
meno invasivo ed il meno pericoloso per la paziente (indipendentemente dal
fatto che le probabilità che la mia diagnosi possa essere giusta siano l’82% o il
99% il trattamento anticoagulante va cominciato)
Come faccio a stabilire la probabilità
pre-test di una malattia (o prevalenza)?
Come faccio a stabilire la probabilità
post-test di una malattia ?
Come faccio a stabilire la probabilità
pre-test di una malattia (o prevalenza)?
• La probabilità pre-test è data dal numero
di individui con la malattia (diagnosi) sul
totale della popolazione a rischio
• Il valore viene ottenuto dagli studi in
letteratura (Riviste scientifiche) o da libri
di testo
Come si esprime una
probabilità?
Due modi equivalenti
• Probabilità
• Possibilità (Odds)
La possibilità (casualità o odds) che si verifichi un evento è data dal numero di volte
che accade (a) diviso per il numero di volte che non accade (b), cioè a/b.
Al contrario, la probabilità che si verifichi un evento è data dal numero di volte che
è accaduto, diviso per il numero di volte che sarebbe potuto accadere, cioè
(a/a+b). I valori di probabilità così calcolati sono sempre compresi tra 0 e 1 (o tra 0
e 100% se espressi in percentuale).
Il rapporto tra due casualità (odds ratio) è il rapporto tra la possibilità che si
verifichi l'evento in un gruppo, diviso per la possibilità che si verifichi lo stesso
evento in un altro gruppo. Per esempio, nel caso si debbano valutare gli effetti sulla
popolazione di un certo tipo di esposizione, l'odds ratio sarà il risultato del rapporto
tra: numero di malati (a) diviso numero di sani (b) nel gruppo esposto, e numero di
malati (c) diviso per il numero di sani i (d) nel gruppo non esposto.
Ad es: 90 individui su 100 in una coorte
di pazienti hanno l’embolia polmonare
• La probabilità è del 90% (o 0.9)
• L’odds è 9:1 (90:10), cioè 9
Ad es: 50 individui su 100 in una coorte
di pazienti hanno l’embolia polmonare
• La probabilità è del 50% (o 0.5)
• L’odds è 1:1 (50:50), cioè 1
Ad es: 10 individui su 100 in una coorte
di pazienti hanno l’embolia polmonare
• La probabilità è del 10% (o 0.1)
• L’odds è 1:9 (10:90), cioè 1.11
Come calcolo gli odds dalle probabilità?
Probabilità 90% = odds 90:10 o 9:1 = 9
Come calcolo la probabilità dagli odds?
Odds 9 = 9/(9+1) = 0.9 o 90%
Come faccio a stabilire la probabilità
post-test di una malattia ?
Due modi:
- A partire da sensibilità e specificità
- A partire dai rapporti di probabilità (oddslikelihood method)
Con entrambi i sistemi io valuto le
caratteristiche operative del test
Probabilità pre-test
Quale è la probabilità
di quella diagnosi in
una coorte di 100
pazienti sovrapponibili
a quello che sto
valutando?
Prevalenza
della malattia

Caratteristiche
operative del test
Il test che voglio
eseguire è in grado di
aumentare o ridurre la
probabilità pre-test
della malattia, e di
quanto?
 Performance
del test
Probabilità post-test
Come valuto la performance di un test diagnostico?
Definizione delle caratteristiche operative
intrinseche del test
- Sensibilità del test
- Specificità del test
La sensibilità e la specificità del test vengono
calcolate usando i risultati del test effettuato su
pazienti precedentemente classificati come sani o
malati mediante un gold standard (un esame o una
procedura di riferimento che dia una diagnosi di
certezza nei malati e sia sempre negativo nei
soggetti sani)
Sensibilità e specificità
Ogni test di laboratorio o strumentale ha delle caratteristiche
intrinseche che riflettono i risultati attesi nei soggetti con la
malattia in questione ed in quelli senza di essa (individui sani)
Tali caratteristiche rispondono fondamentalmente a due quesiti:
1) Quale percentuale di pazienti con la malattia hanno il test
patologico (positivo)?
2) Quale percentuale di soggetti sani hanno il test normale
(negativo)?
La risposta al primo quesito definisce la sensibilità del test, la
risposta al secondo definisce la specificità.
Tali proprietà del test di solito valutate per mezzo di una tabella
binaria, la tabella “2 x 2”
Uso della tabella 2 x 2 per determinare
sensibilità e specificità di un test
Risultato
del test
Malattia presente* Malattia assente*
Positivo
Vero positivo
a
Falso positivo
b
Negativo
Falso negativo
c
Vero negativo
d
Sensibilità
= a/a+c
Specificità
= d/b+d
*In rapporto ad un gold standard,
Il gold standard
• E’ un esame di solito di livello
superiore (dovrebbe avere sensibilità e
specificità del 100%), positivo solo nei
malati, negativo solo nei soggetti sani
• Di solito è un esame invasivo, un
esame autoptico o un follow-up molto
lungo
La sensibilità di un test è la possibilità che un soggetto
malato abbia il test positivo. Viene determinata
identificando la proporzione di soggetti con la malattia nei
quali il test sia positivo (a/a+c).
 La sensibilità si calcola sui malati
La specificità di un test è la possibilità che un soggetto
sano abbia il test negativo. Viene determinata
identificando la proporzione di soggetti sani nei quali il
test sia negativo (cioè d/b+d).
 La specificità si calcola sui sani
I falsi negativi sono dati da 1 – sensibilità, i falsi positivi da
1 – specificità.
malati
sani
Molto positivo
Altri risultati
Sensibility (True positive rate) = 102/251 = 41%
Specificity (True negative rate) = 616/630 = 98%
False negative rate = 149/251 = 59% = 1 – sensibility
False positive rate = 14/630 = 2% = 1 - specificity
Per stabilire le caratteristiche operative di un test la tabella 2 x 2 viene
analizzata in senso verticale, cioè si parte dalla malattia, la presenza o assenza
della quale è stata in precedenza definita in rapporto al gold standard.
Tuttavia la conoscenza delle caratteristiche operative del test di per sé non è
sufficiente a consentire una accurata interpretazione di esso quando applicato al
paziente. Infatti, la conoscenza di sensibilità e specificità ci dicono solamente
quale proporzione di pazienti con o senza la malattia ha il test positivo o
negativo, rispettivamente.
Poiché il compito del medico è quello di stabilire con ragionevole certezza la
presenza o l’assenza della malattia, la questione clinica rilevante sarà: quale è la
probabilità che la malattia sia presente se il test è positivo o che sia assente
se il test è negativo?
Nella pratica clinica di tutti i giorni, la tabella 2 x 2 viene utilizzata quindi in
senso orizzontale, in quanto lo stato di malattia del paziente sottoposto al test
non è noto, mentre invece conosciamo il risultato del test. Si parte quindi dal
risultato del test, e quello che si vuole conoscere è di quanto la positività del test
aumenta la probabilità pretest di malattia, e di quanto la negatività del test
riduce la probabilità pre-test di malattia, cioè in definitiva quali sono le le
probabilità post-test di un esame positivo o negativo
Use of the 2 by 2 table to determine post-test
probabilities given positive and negative results
Test result
Disease present
Disease absent
Positive
True-positive
a
False-positive
b
Post-test probability
of disease given a
positive result
= a/a+b)
Negative
False-negative
c
True-negative
d
Post-test probability
of disease given a
negative result
= c/c+d)
Sensitivity
= a/a+c
Specificity
= d/b+d
Le probabilità post-test di malattia di untest
positivo sono indicate anche come potere
predittivo di un test positivo (PPV o postive
predictive value)
Le probabilità post-test di malattia di un test
negativo sono indicate anche come potere
predittivo di un test negativo (negative positive
value o NPV)
Probability that chest pain is caused by coronary heart disease
(CHD) according to the results of an exercise tolerance test (ETT)
when the pretest estimate of disease probability is 50%
ETT result
CHD present
n = 500
CHD absent
n = 500
Positive
True-positive
n = 430
False-positive
n = 115
Post-test probability
of disease given a
positive result =
430/545 = 79%
Negative
False-negative
n = 70
True-negative
n = 385
Post-test probability
of disease given a
negative result =
70/455 = 15%
Sensitivity
= a/a+c
= 430/500 (86%)
Specificity
= d/b+d
= 385/500 (77%)
Un problema importante della probabilità post-test
come indice di utilità di un esame è che dipende in
maniera significativa dalla prevalenza della malattia
nella popolazione in oggetto  aumenta
all’aumentare della prelenza, indipendentemente
dalla sensibilità e specificità del test
Probability that chest pain is caused by coronary heart disease
(CHD) according to the results of an exercise tolerance test (ETT)
when the pretest estimate of disease probability is 90%
ETT result
CHD present
n = 900
CHD absent
n = 100
Positive
True-positive
n = 774
False-positive
n = 23
Post-test probability
of disease given a
positive result =
774/797 = 97%
Negative
False-negative
n = 126
True-negative
n = 77
Post-test probability
of disease given a
negative result =
126/203 = 62%
Sensitivity
= a/a+c
= 774/900 (86%)
Specificity
= d/b+d
= 77/100 (77%)
Probability that chest pain is caused by coronary heart disease
(CHD) according to the results of an exercise tolerance test (ETT)
when the pretest estimate of disease probability is 10%
ETT result
CHD present
n = 100
CHD absent
n = 900
Positive
True-positive
n = 86
False-positive
n = 207
Post-test probability
of disease given a
positive result =
86/293 = 29%
Negative
False-negative
n = 14
True-negative
n = 693
Post-test probability
of disease given a
negative result =
14/707 = 2%
Sensitivity
= a/a+c
= 86/100 (86%)
Specificity
= d/b+d
= 693/900 (77%)
Un altro metodo per valutare l’utilità di un test è
quello basato sul concetto di likelihood ratio (invece di
sensibilità e specificità)
Un likelihood ratio (LR) è un rapporto tra probablità
che indica di quante volte un test è in grado di
aumentare un odds di malattia se positivo (LR+), o di
quante volte un test è in grado di ridurre un odds di
malattia se negativo (LR-)  il prodotto tra odds pretest ed LR darà un odds post-test
A differenza delle probabilità posttest i valori di LR sono indipendenti
dalla prevalenza della malattia
Le probabilità post-test possono
comunque essere poi ricalcolate dai
valori di odds post-test
Odds
An odds expression compares the likelihood that a
particular outcome (for example a disease being
present) will occur to the likelihood that it will not
occur
Probabilities can be transformed in odds
A 75% probability corresponds to a 3:1 odds (75%:25%)
Odds can be transformed in probabilities
A 3:1 odds corresponds to a 75% probability i.e. 3/(1+3)
malati
sani
Molto positivo
Altri risultati
102/51
14/630
= 0.406
= 0.022
LR+ = 0.406/0.022 = 18.3
(sensibilità/(1-specificità)
Example
Pre-test probability of a X disease 60%
Sensitivity 90%
Specificity 91%
a) Calculate pre-test odds from pre-test probability
pre-test odds = 60:40 = 1.5
b) Obtain from the literature or calculate LR for positive test
LR+ 0.90/0.09 = 10
c) Multiply pre-test odds for LR to obtain post-test odds
post-test odds = 10x1.5 = 15
d) Transform post-test odds to post-test probabilities
post-test probability = 15/(15+1) = 94%
The utilization of the test (in the case of a positive test) has
increased the pre-test probability of the X disease form 60% to
94%
Dove si trovano le probabilità pre-test e gli LR?
Probabilità pre-test
- Studi osservazionali
- Gruppi placebo di RCT
LR+ ed LR- Riviste scientifiche (Articoli)
- Libri di testo
Pubmed
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi
oppure
Entrare nel sito (gratuito) attraverso il sito web
della Biblioteca Centrale Facoltà di Medicina Parma
Libri di testo di Evidence-Based Medicine (EBM)
(medicina basata sulle prove di efficacia)
Straus SE et al.,
Evidence-based Acute Medicine.
Churchil-Livingstone, 2002
Guyatt GG, Rennie D
Users’ guide to the medical literature.
American Medical Association 2002
(www.ama-assn.org)
Appendicite acuta
Prevalenza nella popolazione in esame 20%
Dolore addominale nel quadrante inferiore dx: LR+ 2.2
TAC spirale addome con mezzo di contrasto per os LR+ 26
Prevalenza 20%  Pre-test odds 20:80, cioè 1:4, cioè 0.25
Post-test odds dopo esame obiettivo = 0.25 x 2.2 = 0.55
La probabilità post-test sarà 0.55/(1+0.55) = 35.4%
Post-test odds dopo esame obiettivo e TAC spirale =
0.25 x 2.2 x 26 = 14.3
La probabilità post-test sarà 14.3/(1+14.3) = 93.4%
Il valore di LR ratio mi può già dare
una idea dell’utilità di un test anche
senza calcolare le probabilità posttest, e senza conoscere la prevalenza
di un problema clinico
Utilità di un test in base al valore
di LR ratio che lo caratterizza
Utilità
LR+
LR-
Eccellente*
10
0.1
Buono
6
0.2
Discreto
2
0.5
Inutile
1
1
* Variazioni importanti e conclusive dalla probabilità pre-test a quella post-test