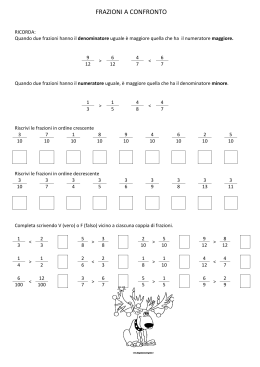
16o RMT
maggio 2008
Finale
©ARMT.2008
15
15. FRAZIONI SOVRAPPOSTE (Cat. 7, 8, 9, 10)
Gianni e Lina hanno disposto ciascuno nove numeri su tre righe e tre colonne e hanno inserito sei
linee tra due numeri sovrapposti: possono così leggere sei frazioni.
Ecco la disposizione di
Gianni:
2 4 6
ed ecco quella di
4 3 2
8 12 9
Lina:
8 6 9
10 16 18
14 16 15
I ragazzi hanno scelto i loro numeri cercando di rispettare le seguenti regole:
a) i nove numeri sono numeri naturali tutti diversi tra loro;
b) ognuna delle sei frazioni che si possono leggere rappresenta un numero più piccolo di 1;
c) nessuna delle sei frazioni è ridotta ai minimi termini;
d) tutte le frazioni rappresentano numeri diversi fra loro.
Inoltre Gianni e Lina hanno scelto i nove numeri cercando di fare in modo che il più grande tra essi
fosse il più piccolo possibile.
Lina è molto soddisfatta perché il suo numero più grande (16) è minore del più grande dei numeri di
Gianni (18).
Ma Gianni le fa osservare che lei non ha rispettato la regola d), poiché 4/8 = 3/6, né la regola c),
dato che 2/9 è una frazione ridotta ai minimi termini.
Scegliete anche voi nove numeri rispettando le quattro regole come Gianni, ma in modo che il
numero più grande sia minore di 18 e sia il più piccolo possibile.
Scrivete la vostra scelta migliore.
ANALISI A PRIORI
Ambito concettuale
Aritmetica: frazioni, semplificazioni, frazioni equivalenti, numeri primi tra loro
Analisi del compito
- Rendersi conto che non si può scegliere 1 (altrimenti la frazione sarebbe ridotta ai minimi termini), che due numeri sovrapposti
devono avere un divisore comune, e che i numeri di una stessa colonna sono ordinati dal più piccolo al più grande.
- Nel corso dei tentativi, notare che bisogna scegliere dei numeri piccoli nella prima riga, che è vantaggioso annotarsi le frazioni
semplificate per evitare le frazioni equivalenti, che se si scelgono solo numeri pari, si è sicuri che tutte le frazioni saranno
semplificabili, ma non si scenderà al di sotto di 9 x 2 = 18, e così via.
- Partire dunque da 2 e fare man mano l’elenco dei numeri ancora utilizzabili: 3, 4 (non 5) 6, (non 7), 8, 9 (a denominatore del 6),
10, (non 11) 12 , (non 13) e 14.
Oppure partire ipotizzando il numero più grande (ad esempio 16) e cercare gli altri seguendo le regole. Provare poi con 15 e con 14 e
rendersi infine conto che con 12 non esiste alcuna soluzione.
Ecco qui di seguito qualche soluzione, di cui le prime due non ottimali:
2
4
3
2
4
3
2
3
4
8
6
9
10
8
9
8
6
12
14
16
15
15
14
12
10
9
14
2
3
4
2
3
4
2
3
4
6
12
8
8
9
6
8
9
6
4
9
10
9
14
10
14
12
10
10
12
14
6
12
14
punteggio 4 :
2
3
8
Risposta corretta: disposizione corretta e ottimale di 9 numeri naturali, di cui 14 è il numero più grande utilizzato
(è il minimo possibile)
Livello: 7, 8, 9, 10 Origine: Israel
6o RALLY MATEMATICO TRANSALPINO - PROVA I
12• FRAZIONE DI UN TERRENO
gennaio 1998
©ARMT
Giuseppe possiede un appezzamento di
terreno a forma di quadrato e, poiché è un
po' giocherellone, lo divide con rette
passanti per i vertici o per i punti medi
(cioè i punti di mezzo) dei lati del
quadrato.
Francesco riceverà in eredità la parte
ombreggiata del terreno di suo padre
Giuseppe.
Quale frazione del terreno riceverà
Francesco?
Giustificate la vostra risposta.
Campo concettuale:
- Geometria: figure equivalenti, rette parallele, punti medi
- Aritmetica: frazioni
Analisi del compito:
- Ricomporre le sei parti in un parallelogramma e in due triangoli rettangoli isometrici
- Trovare che l'area di ognuno di questi triangoli è la metà di quella del quadrato
- Dedurre che l'area del parallelogramma è metà dell'area del quadrato
- Trovare quindi che la parte ombreggiata, essendo metà del parallelogramma, vale un
quarto dell'area del quadrato
Livello : 6 - 7 - 8
Origine : Bourg en Bresse
FINE CAT. 6
13
17° RMT
PROVA II
marzo - aprile 2009
©ARMT.2009
10
14. ATTRAVERSAMENTO DEL FIUME (Cat. 6, 7, 8) ©ARMT 2009 - 17° - II prova
Un gruppo di turisti, tra 100 e 200 persone, deve attraversare un grande fiume, ma l’unico ponte
esistente è stato distrutto dalle intemperie. Sono però disponibili due barche: una piccola ed una
grande.
Con la piccola, utilizzata ogni volta al completo, tutti i turisti potrebbero attraversare il fiume in
21 viaggi.
Con la grande, anch’essa utilizzata ogni volta al completo, tutti i turisti potrebbero attraversare il
fiume in solo 9 viaggi.
Dopo 5 viaggi di ciascuna delle due barche, restano ancora dei turisti da trasportare.
Secondo voi, quanti?
Spiegate il vostro ragionamento.
ANALISI A PRIORI
Ambito concettuale
- Aritmetica: multipli comuni; frazioni (addizioni)
Analisi del compito
- Tenere presente che il numero dei turisti è compreso fra 100 e 200.
- Comprendere che questo numero è un multiplo comune di 21 e di 9, quindi di 63.
- Trovare i multipli di 63 compresi tra 100 e 200. Essi sono due: 126 e 189.
- Considerare che, se i turisti sono 126, con la barca piccola, si possono trasportare 6 turisti (126 : 21 = 6) in ogni
viaggio, mentre con la barca grande 14 turisti (126 : 9 = 14) in ogni viaggio.
- Calcolare allora che dopo 5 viaggi delle due barche sono stati trasportati 100 turisti (6 × 5 = 30 e 14 × 5 = 70) e
che, quindi, ne restano ancora 26 da trasportare.
- Analogo ragionamento nel caso di 189 turisti: ad ogni viaggio, con la barca piccola si possono trasportare 9
turisti (189 : 21), mentre con la barca grande 21 turisti (189 : 9). Dopo 5 viaggi di ogni barca, hanno potuto
attraversare il fiume 150 turisti (9 × 5 + 21 × 5 = 150), ne restano quindi ancora 39 da trasportare.
Oppure, usando le frazioni:
- Rendersi conto che il numero dei turisti trasportati in ogni viaggio dalla barca piccola è 1/21 del totale, mentre il
numero dei turisti trasportati in ogni viaggio dalla barca grande è 1/9. Ne segue che, dopo 5 viaggi di entrambe le
barche, il numero complessivo dei turisti trasportati è 5/21 + 5/9 = 50/63 del totale.
- Comprendere che il numero totale dei turisti deve essere un multiplo di 63, maggiore di 100 e minore di 200:
126 o 189.
- Calcolare, nei due casi, con la frazione complementare (1 – 50/63 = 13/63) il numero dei turisti ancora da
trasportare: 126 × 13/63 = 26 o 189 × 13/63= 39.
Attribuzione dei punteggi
4 Le due soluzioni (26 o 39 turisti) con giustificazione completa
3 Una soluzione esatta con giustificazione corretta e l’altra con un errore di calcolo
2 Le due soluzioni esatte senza giustificazione,
oppure due soluzioni sbagliate a causa di errori di calcolo, ma con procedimento corretto,
oppure una sola soluzione esatta con giustificazione
1 Una soluzione esatta senza giustificazione,
oppure una soluzione sbagliata ma con procedimento corretto
0 Incomprensione del problema.
Livello: 6, 7, 8
Origine: Ticino
17° RMT
PROVA I
gennaio - febbraio 2009
©ARMT.2009
2
7. BUDINO AL CIOCCOLATO (Cat. 4, 5, 6) ©ARMT 2008 - 17° - I prova
Doris, Francesca e Ben hanno bisogno di 150 grammi di
cioccolato per preparare un budino al cioccolato.
Ognuno di loro prende una tavoletta di cioccolato da 200
grammi, come quella disegnata qui accanto, e decide di tagliarla
seguendo le sue linee.
Doris taglia la sua tavoletta in tre parti, una delle quali è un rettangolo di 150 grammi.
Francesca taglia la sua tavoletta in due sole parti, una delle quali è anch’essa un rettangolo di 150
grammi.
Ben taglia anche lui la sua tavoletta in due parti, di cui l’una è un rettangolo di 150 grammi, ma più
lungo di quello di Doris e di Francesca.
Disegna un rettangolo come quello di Doris, un rettangolo come quello di Francesca e un
rettangolo come quello di Ben, seguendo le linee delle loro tavolette.
Fate tre diversi disegni.
Spiegate perché ognuno di questi rettangoli pesa 150 grammi.
ANALISI A PRIORI
Ambito concettuale:
-
Geometria: rettangolo
Aritmetica: proporzionalità, frazioni elementari
Analisi del compito
-
Rendersi conto che è necessario passare da 200 g - la tavoletta intera - a 150 g, e che il problema è di determinare
quale sarà la parte di tavoletta che si dovrà conservare, mantenendo una forma rettangolare.
- Rendersi conto che se la tavoletta intera pesa 200 g, la metà pesa 100 g e la metà della metà (ovvero un quarto), pesa
50 grammi e che si dovrà dunque togliere un quarto della tavoletta o conservarne i tre quarti.
- Visualizzare allora le parti rettangolari che possono rappresentare un quarto o tre quarti (rispettivamente 1 o 3 file
« orizzontali » o 2 o 6 file « verticali »).
Oppure : immaginare la scomposizione in quadrati : contare i quadrati (32), e prenderne la metà e il quarto per
determinare che per il budino al cioccolato occorreranno 24 quadrati, che possono formare un rettangolo di 3 x 8 o
di 4 x 6.
Oppure : calcolare il peso di un quadrato (200 : 32 = 6,25) e determinare quanti quadrati saranno necessari per il budino
(150 : 6,25 = 24), poi constatare che i rettangoli possibili di 24 quadretti sono quelli di dimensioni 3 x 8 o 4 x 6.
- Osservare che ci sono solo due disposizioni di un rettangolo di 4 x 6 sulla tavoletta (che non sono simmetriche l’una
dell’altra) e una sola disposizione di un rettangolo di 3 x 8 (con una isometria) e constatare, partendo dalle
affermazioni di ognuno, che il rettangolo di Doris è ottenuto con due tagli nel senso della larghezza, quello di
Francesca con un solo taglio nel senso dalla larghezza e quello di Ben con un taglio nel senso dalla lunghezza :
Doris
Francesca (per es.)
Ben (per es.)
Attribuzione dei punteggi
4 I tre rettangoli di Doris, Francesca e Ben (come si vede sopra) disegnati chiaramente e identificati con spiegazioni su
come passare da 32 a 24 quadretti e sulle due scomposizioni possibili di 24: 3 x 8 e 4 x 6
3 I tre rettangoli disegnati chiaramente, con delle spiegazioni poco chiare sui “24 quadretti”
2 I tre rettangoli disegnati chiaramente e identificati, senza altre spiegazioni
o due rettangoli disegnati chiaramente, con spiegazioni
1 Individuato uno solo dei rettangoli o solamente l’area di 24 quadretti
0 Incomprensione del problema
Livello: 4, 5, 6
Origine: Luxembourg
13o RALLY MATEMATICO TRANSALPINO – PROVA II - marzo, aprile 2005 ©ARMT.2005
p. 10
9. I COMPAGNI DI GIUDITTA (Cat. 5, 6)
Giuditta ha notato che, nella sua classe, ci sono alcuni alunni che hanno i capelli neri e gli occhi azzurri.
Poiché Giuditta è curiosa di natura, si mette ad osservare tutti gli alunni delle quattro classi della sua
scuola.
Dopo qualche giorno, scopre che:
- la metà degli alunni sono maschi
- un terzo degli alunni hanno i capelli neri
- dividendo il numero degli alunni della scuola per 7, si trova il numero degli alunni che hanno gli occhi
azzurri,
- in ciascuna classe, ci sono almeno 20 alunni ma non più di 30.
Quanti sono gli alunni delle classi osservate da Giuditta che non hanno gli occhi azzurri?
Spiegate come avete trovato la vostra soluzione.
ANALISI A PRIORI
Ambito concettuale
-
Aritmetica: frazioni, multipli, divisibilità, confronto di numeri
Analisi del compito
-
Capire che il numero degli studenti deve essere un multiplo di 2, di 7 e di 3 e quindi di 42 che è il loro m.c.m.: 42, 84, 126,
168,….
- Esaminare i numeri precedenti (multipli) in rapporto ai valori 80 (20x4) e 120 (30x4), che sono il minimo e il massimo
possibili di allievi
- Concludere che gli studenti osservati sono in tutto 84, e che quindi 84 – (1/7) 84 = 72 (oppure (6/7) 84 ) è il numero degli
allievi che non hanno gli occhi azzurri.
Oppure (per gli allievi che non conoscono il m.c.m.)
- Situare il numero degli alunni tra 80 e 120 (secondo l’ultima indicazione), poi cercare in questo intervallo numeri che sono
divisibili per 7 (a partire da 70 o 77: 84, 91, 98, 105, 112 e 119), eliminare quindi i dispari (restano solo 84, 98 e 112) e
trovare che 84 è il solo numero ancora in lista che è divisibile per 3.
- Calcolare come in precedenza il numero degli allievi che hanno gli occhi azzurri: 84 : 7 = 12 e sottrarre questo risultato da
84 per conoscere il numero degli allievi che non hanno gli occhi azzurri.
Livello: 5 - 6
Origine: Parma
e
8 RALLY MATEMATICO TRANSALPINO
©ARMT 2000
FINALE - maggio 2000
9. LA CURA (cat. 5, 6, 7)
Anna non si sente bene e il suo medico le ha prescritto una cura.
Il farmacista legge la ricetta del medico e dà ad Anna una confezione, di 40 compresse,
sulla quale scrive la seguente prescrizione:
"Da prendere prima dei pasti con un bicchiere d'acqua:
- i primi tre giorni: una mezza compressa al mattino e una compressa la sera
- i tre giorni seguenti: una compressa a mezzogiorno e un quarto di compressa la sera
- i tre giorni seguenti: un quarto di compressa al mattino
- i tre giorni seguenti: una mezza compressa la sera
lasciar passare due giorni senza prendere compresse e poi ricominciare come prima".
Quanti giorni durerà la cura con la confezione di 40 compresse?
Giustificate la vostra risposta.
ANALISI A PRIORI
Ambito concettuale:
- Aritmetica: operazioni con numeri con la virgola o con frazioni
- Logica
Analisi del compito:
- Capire che il numero di compresse cambia ogni tre giorni
- Calcolare quante compresse prende Anna per gruppi di tre giorni e quindi per 12 giorni:
giorni :
compresse :
3
9/2 = 4,5
3
15/4 = 3,75
3
3/4 = 0,75
3
3/2 = 1,5
12
42/4 = 21/2= 10,5
-
Tener conto dei due giorni di pausa per ogni ciclo, cioè: 14 giorni per10,5 compresse
-
Capire che per i primi tre cicli : 42 giorni (14 + 14 + 14), Anna prenderà 63/2 = 31,5 compresse
-
Capire che nella confezione ci saranno ancora (40 - 31,5) compresse = 8,5 compresse e quindi 7 giorni
(in quanto 8.25 compresse in sei giorni, le ci vorrà quindi ancora un giorno per 1/4 di compressa), in tutto
49 giorni (42 + 7)
-
Oppure procedere giorno per giorno
Valutazione:
4 Risposta corretta (49) e giustificazione con i dettagli
3 Risposta corretta con giustificazione poco chiara
2 Calcolo corretto delle compresse necessarie per tre cicli (in 42 giorni 31,5 compresse) con i dettagli, o
risposta corretta senza dettagli e senza giustificazione
1 Calcolo corretto delle compresse necessarie per un ciclo (in 12 giorni 10,5 compresse)
0 Incomprensione del problema
Livello: 5 - 6 - 7
Origine : Parma, incontro di Siena
10. CAMPIONATO DI PALLACANESTRO (cat 6, 7, 8)
Le sei scuole della città partecipano tutti i mercoledì al campionato di pallacanestro.
Le regole sono quelle dei campionati degli adulti: