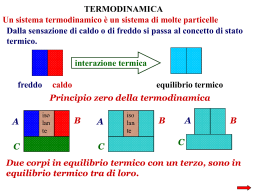
Seconda Scuola Estiva AIF
per studenti della Scuola Superiore
Fondamenti di
Termodinamica
Vincenzo Orofino
Dipartimento di Fisica, Università del Salento
Richiamo concetti basilari di dinamica
Pressione esercitata da una forza:
F
p 
A
Energia meccanica (totale):
E  Ek  E p
1
 mv2  m g h
2
Teorema lavoro-energia:
E  L fd
Sistemi termodinamici
Importante risultato sperimentale: ogni volta che si dissipa
energia meccanica, hanno luogo fenomeni di riscaldamento.
Ad esempio nel caso del pendolo si riscalda il punto di
sospensione; nell’auto che si ferma si riscaldano i freni, ecc.
La termodinamica è quella parte della fisica che descrive i
processi di riscaldamento o raffreddamento (fenomeni
termici) e l loro correlazione con i processi dinamici.
Il sistema è il corpo o l’insieme dei corpi sotto esame.
L’ambiente esterno è l’insieme di tutti i corpi che possono
interagire con il sistema.
Parametri di stato
Un sistema macroscopico viene descritto ricorrendo a
grandezze macroscopiche d’insieme che descrivono
caratteristiche del sistema nel suo complesso. Tali
grandezze sono dette parametri di stato (o variabili
termodinamiche).
Parametri di stato sono il volume, la pressione, la massa
volumica, la temperatura ecc.
Lo stato di un sistema termodinamico è definito quando i
valori dei parametri di stato sono univocamente
determinati.
Agitazione termica
Un qualunque fluido è costituito da un gran numero di
particelle (sia singoli atomi che molecole) in un continuo moto
disordinato definito agitazione termica.
Questo fenomeno sta alla base dei cosiddetti moti browniani.
Moto browniano di una
microparticella di resina di raggio
intorno a 3 micron. I punti,
congiunti con segmenti,
rappresentano le successive
posizioni della particella osservata
al microscopio ad intervalli di 30 s
da un punto iniziale A ad uno
finale B.
Temperatura
La temperatura è una grandezza correlata all’energia
cinetica media della particelle di un sistema.
In particolare, per un gas a bassa pressione (gas ideale):
Ek , med
3
 kT
2
dove k è una costante e T è la temperatura del sistema
misurata in un’opportuna unità di misura chiamata kelvin
(vedi in seguito).
Equilibrio termico (1)
Si considerino due sistemi A e B, come in figura, inizialmente
posti a temperature TA e TB, rispettivamente (con TA < TB).
Equilibrio termico (2)
Finché i sistemi sono separati da una parete adiabatica (caso
a) le loro temperature non cambiano.
Se la parete adiabatica viene rimossa o sostituita con una
parete diatermica (caso b), dopo un adeguato tempo i due si
portano entrambi ad una stessa temperatura T (TA < T < TB).
Una volta raggiunta questa situazione si dice che i due
sistemi sono in equilibrio termico.
Principio zero – Calore (1)
Principio zero della termodinamica:
Due sistemi interagenti fra loro, ma isolati dall’ambiente
esterno, si portano all’equilibrio alla stessa temperatura.
Se due corpi a diversa temperatura vengono messi a
contatto, il corpo più caldo cede calore al più freddo.
Il calore è l’energia scambiata da due corpi (o tra due parti
dello stesso corpo) a causa della loro diversa temperatura.
Principio zero - Calore (2)
Quando due sistemi sono in equilibrio termico, tra di essi non
si verifica nessuno scambio netto di energia sotto forma di
calore.
Il calore può trasformarsi in energia meccanica, così come
l’energia meccanica può trasformarsi in calore.
La termodinamica studia i fenomeni nei quali si verificano
trasformazioni di calore in altre forme di energia, oppure le
trasformazioni inverse.
Termometri: scala centigrada (1)
Il metodo di taratura si attua assegnando per convenzione i
valori:
T = 100 °C alla temperatura dell’acqua pura al punto di
ebollizione in atmosfera standard;
T = 0 °C alla temperatura dell’acqua pura al punto di
congelamento in atmosfera standard.
In linea di principio il termometro misura una qualunque
grandezza X che dipende dalla temperatura (l’altezza di una
colonna di liquido, la resistenza elettrica di un conduttore, la
pressione di un gas, ecc.).
Termometri: scala centigrada (2)
Il procedimento di misura si attua in due stadi:
1) Si pone il termometro in equilibrio termico con acqua pura
prima al punto di ebollizione e poi al punto di congelamento,
misurando i due valori X100 e X0, rispettivamente.
2) Si pone il termometro in equilibrio termico con il corpo di
cui si vuole determinare la temperatura, misurando per la
grandezza termometrica il valore X.
Assumendo una dipendenza lineare dell grandezza termometrica
dalla temperatura, si ha:
T  (100
X  X0
) C
X 100  X 0
Termometri: scala Kelvin (1)
La scala Kelvin si basa sull’osservazione che esiste un limite
inferiore alla temperatura che un qualunque corpo può assumere.
Tale limite viene assunto come lo zero di questa scala
termometrica (T = 0 K, zero assoluto).
Per convenzione si assegna alla temperatura dell’acqua pura al
punto triplo in atmosfera standard l’esatto valore T = 273.16 K.
N.B.: Si definisce punto triplo, quella particolare configurazione
fisica dell’acqua pura in cui le sue tre fasi di aggregazione (solida,
liquida e aeriforme) coesistono in equilibrio.
Termometri: scala Kelvin (2)
Il procedimento di misura si attua in due stadi:
1) Si pone il termometro in equilibrio termico con acqua pura
al punto triplo, misurando il valore Xtr.
2) Si pone il termometro in equilibrio termico con il corpo di cui
si vuole determinare la temperatura, misurando per la grandezza
termometrica il valore X.
Assumendo una proporzionalità diretta tra la grandezza
termometrica e la temperatura (X = 0 per T = 0 K), si ha:
X
T  (273.16
)K
X tr
Termometri: scala Kelvin (3)
La relazione tra il valore della temperatura in gradi centigradi
(TC) e quella assoluta in kelvin (T ) è:
TC = T – 273.15
La temperatura del ghiaccio fondente (ossia la temperatura del
punto di congelamento dell’acqua) è pari a 273.15 K.
La temperatura dello zero assoluto è TC = – 273.15 °C.
E’ importante notare che:
T C = 1 °C  T = 1 K
Equazione di stato di un gas ideale (1)
Si definisce gas perfetto o ideale un gas le cui proprietà
rappresentano il comportamento limite dei gas reali quando la
loro massa volumica (densità) tende a zero.
Per i gas perfetti esiste la seguente relazione empirica tra
pressione p, volume occupato V, numero di molecole N e
temperatura assoluta T (equazione di stato del gas perfetto):
pV  N k T
dove k = 1.38  1023 J/K è la cosiddetta costante di
Boltzmann.
Equazione di stato di un gas ideale (2)
Due variabili termodinamiche (in genere p e V) sono sufficienti
per descrivere lo stato di un gas ideale.
Lo stato di un gas ideale è rappresentato da un punto in un
diagramma cartesiano V-p (detto piano di Clayperon).
Trasformazioni termodinamiche (1)
Un sistema compie una trasformazione termodinamica se,
agendo dall’esterno, si varia almeno una delle sue variabili
termodinamiche.
Durante una trasformazione il sistema non può essere isolato:
esso scambia energia con l’ambiente.
Rappresentazione grafica nel piano di
Clayperon di trasformazioni termodinamiche
tra due stati A e B.
Trasformazioni termodinamiche (2)
Una trasformazione durante la quale:
il sistema non scambia calore con l’ambiente, è detta
trasformazione adiabatica;
resta costante il volume del sistema, viene chiamata
trasformazione isovolumica (o isocora);
resta costante la pressione del sistema, viene detta
trasformazione isobara;
resta costante la temperatura del sistema, è chiamata
trasformazione isoterma.
Lavoro (1)
Un modo per trasferire energia dall’ambiente al sistema (o
viceversa) è quello di compiere lavoro sul sistema (o far compiere
lavoro al sistema).
Si consideri un gas contenuto all’interno di cilindro isolato
termicamente chiuso da un pistone mobile (v. figura).
Lavoro (2)
La forza F’, che il gas esercita sul pistone (risultante dagli
urti tra molecole del gas e pistone), produce uno spostamento dx
del pistone stesso.
Lo scambio di energia tra sistema ed ambiente esterno si
può esprimere come il lavoro compiuto da tale forza:
dL   F  dx  p A dx  p dV
(lavoro infinitesimo compiuto sull’ambiente dal gas a pressione
p),
Lavoro (3)
oppure come il lavoro compiuto dalla forza che il pistone
esercita sulle molecole del gas:
dL   F dx   p A dx   p dV
(lavoro infinitesimo compiuto dall’ambiente sul gas).
Per una variazione finita di volume da Vi a Vf, il lavoro
compiuto dal gas è:
Vf
L 
 p dV
Vi
Lavoro (4)
Il lavoro compiuto dall’ambiente sul sistema è invece:
Vf
L 
 p dV
  L
Vi
Il modulo del lavoro eseguito sul
gas è uguale all’area sottesa dalla
curva che rappresenta la funzione
p = p(V). Il segno di L è
determinato dalla disuguaglianza
tra Vi = V1 e Vf = V2.
Lavoro (5)
Importanti casi particolari
Lavoro svolto a volume costante
Per qualsiasi trasformazione in cui il volume rimanga costante
(isocora) il lavoro è nullo.
L 0
(V  costante)
Lavoro svolto a pressione costante
In una trasformazione di questo tipo (isobara) si ha:
Vf
Vf
L    p dV   p  dV   p (V f  Vi )
Vi
Vi
( p  costante)
Calore (1)
Secondo la teoria fluidistica il calore era concepito come una
sostanza imponderabile (fluido calorico o semplicemente calorico)
permeante tutti i corpi.
Mettendo a contatto due corpi a diversa temperatura si
pensava che tale fluido passasse dal corpo a temperatura
maggiore a quello a temperatura minore fino a quando i due corpi
avessero raggiunto la stessa temperatura.
Secondo questa teoria un corpo risultava più caldo di un altro
poiché possedeva una maggiore quantità di fluido calorico.
Tale errata concezione del calore fu abbandonata quando si
intuì che il calore non è altro che una forma di energia.
Calore (2)
Si riconsideri il sistema in figura già discusso in precedenza.
In tal caso la variazione di energia interna del sistema è:
Vf
Eint  L  
 p dV
Vi
Calore (3)
Tale equazione esprime una media macroscopica che
considera tutti i singoli scambi di energia tra le molecole del gas e
quelle dell’ambiente (pistone).
Tali scambi energetici avvengono in genere non solo quando
le pareti del contenitore sono mobili ma anche quando sono fisse.
Consideriamo un gas all’interno di un contenitore rigido dalle
pareti diatermiche. Se si riscaldano le pareti del contenitore, si può
osservare un aumento di temperatura del gas e quindi di energia
interna.
Calore (4)
In questo caso l’equazione precedente, che rappresenta il
principio di conservazione dell’energia meccanica, è inadatta a
descrivere gli scambi energetici tra sistema e ambiente poiché non
ci sono parti in movimento e quindi non c’è variazione di volume.
Calore (5)
Si introduce quindi un nuovo concetto statistico chiamato
calore che rappresenta il valor medio dell’energia scambiata tra
sistema e ambiente, sempre a causa delle collisioni tra le molecole
dell’uno e dell’altro, energia che non può essere
macroscopicamente espressa come un lavoro meccanico.
Il calore è la somma di un grandissimo numero di lavori
infinitesimi individuali, tali da non poter essere espressi
complessivamente, a livello macroscopico, come il prodotto di una
forza per uno spostamento medio.
In tal caso (trasformazione isocora) la variazione di energia
interna del sistema vale:
Q = 0  Trasformazione adiabatica
Calore ed equilibrio termico
Quando tra ambiente e sistema (o tra due sistemi) non si
verifica alcuno scambio netto di energia sotto forma di calore, si
dice che essi sono in equilibrio termico.
Il calore è una forma di energia in transito che passa da un
sistema all’ambiente esterno o viceversa quando tra sistema ed
ambiente vi è una differenza di temperatura.
Calore e lavoro
Analogie tra calore e lavoro
•Il calore, come il lavoro, non è una proprietà intrinseca di un
sistema.
•La quantità di calore che il sistema assorbe o cede in una
trasformazione dipende dal tipo di trasformazione.
1) L  Q : è sempre possibile la trasformazione integrale
2) Q  L : non è possibile la trasformazione integrale
(altrimenti sarebbe possibile il cosiddetto moto perpetuo di
seconda specie)
Calore e temperatura
Differenze tra calore e temperatura
I concetti di calore e temperatura sono distinti.
a) Si può aumentare la temperatura di un corpo senza cedergli
calore (durante una compressione adiabatica).
b) Si può cedere calore ad un corpo senza far variare la sua
temperatura (durante un processo di fusione o di
evaporazione).
Calore: unità di misura
Caloria (Piccola caloria) = 1 cal
la quantità di calore necessaria per innalzare da 14.5 a 15.5 °C la
temperatura di 1 g di acqua.
Grande caloria = 1 Cal =1000 cal = 1 Kcal
1 cal = 4.186 J
1 Kcal = 4186 J
Calore specifico (1)
Si definisce calore specifico (o capacità termica specifica) del
materiale che costituisce un corpo di massa m, il rapporto:
C
Q
c 
m m T
A temperature ordinarie e per ordinari intervalli di temperatura, c
è praticamente costante. La quantità di calore Q necessaria per
aumentare la temperatura di un corpo di massa m da un valore
iniziale Ti ad uno finale Tf vale quindi:
Q  m c (T f  Ti )
Calore specifico (2)
Sostanza
c [J/(kg  K)]
Piombo
129
Tungsteno
135
Argento
236
Rame
Sostanza
c [J/(kg  K)]
Mercurio
139
Etanolo
2430
Acqua
4190
387
Alluminio
900
Carbonio
502
Sorgenti di calore e termostati
Si definisce sorgente termica qualsiasi corpo che sia in grado di
fornire calore ad uno o a più altri corpi.
Il calore si ottiene sempre come il risultato della trasformazione
di altre forme di energia.
Viene chiamato invece termostato un particolare corpo in grado
di fornire o assorbire calore senza che ciò modifichi
apprezzabilmente la sua temperatura. Un termostato è un
qualunque corpo massivo costituito da una sostanza con un
elevato calore specifico.
Primo principio della termodinamica (1)
In una trasformazione adiabatica:
Eint  L
In una trasformazione isocora:
Eint  Q
In una trasformazione generica:
Eint  L  Q
(Primo principio della termodinamica)
Primo principio della termodinamica (2)
Il primo principio della termodinamica rappresenta l’applicazione
del principio di conservazione dell’energia a sistemi aventi un
gran numero di particelle.
Pressione (1)
Pressione ordinaria
Data una forza di modulo F agente su una superficie di area
A come in figura, si definisce pressione esercitata dalla forza
il rapporto:
F cos  FN
p

A
A
con FN componente della forza
normale alla superficie.
Pressione (2)
Pressione interna di un fluido
Si chiama pressione interna di un fluido in un punto P la
pressione esercitata dal fluido su una superficie di area
A centrata intorno a P (dovuta agli urti delle molecole
del fluido contro la superficie stessa).
La pressione interna di un
fluido è indipendente dalla
giacitura di A e dalla
forma del contenitore.