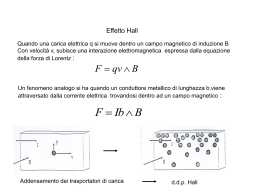
Tesina Fisica Generale II
Corso di Laurea in Scienza ed Ingegneria dei
materiali
Gruppo IV: Gallo Elia
Russo Adriano
N50000299
N50000286
Il magnetismo
Gli effetti del campo magnetico sono conosciuti dall’uomo da molto prima che questo fosse a
conoscenza dei fenomeni elettrostatici. Probabilmente, nella Cina del XIII secolo a.C. era conosciuta ed
utilizzata la bussola, mentre è certo che fin dall’800 a.C. i Greci conoscevano le proprietà di alcuni
materiali, le magnetiti, capaci di attrarre piccoli pezzi di ferro. Grazie al lavoro svolto negli ultimi secoli
da numerosi scienziati, molte scoperte sono state fatte nel campo del magnetismo.
Oggi sappiamo che i fenomeni magnetici sono dovuti agli spin degli elettroni e alle correnti elettriche.
Queste ultime generano campi magnetici che, a loro volta, determinano forze magnetiche che agiscono
sulle cariche elettriche in movimento e sugli spin degli elettroni.
Il campo magnetico è un campo vettoriale, così come il campo elettrico. Le linee di campo magnetico
sono sempre linee chiuse.
Graficamente si adotta la seguente convenzione per rappresentare le linee di campo magnetico:
. Vettore campo magnetico uscente dal piano
Vettore campo magnetico entrante nel piano
La forza di Lorentz nel caso particolare 𝑬=0
Consideriamo una carica q in moto con velocità 𝑣 in presenza di un campo
magnetico uniforme 𝐵. Sperimentalmente, si osserva che la carica q è
sottoposta ad una forza magnetica definita dalla seguente legge:
𝑭m=q(𝒗×𝑩)
Fig. 1 Direzione e verso del vettore 𝒗×𝑩 si determinano con la regola della mano destra (fig.1). Il verso è poi
definito dal segno della carica di prova q: se q>0 allora il verso della forza sarà quello in fig. 1, se q<0 il
verso sarà opposto.
Il modulo della forza magnetica è dato dalla seguente equazione:
F = qvBsenθ
dove θ è l’angolo compreso tra il vettore 𝑣 e il vettore 𝐵.
La forza magnetica ha come effetto quello di cambiare la direzione del moto di una carica, ma non il
modulo della sua velocità. Il lavoro compiuto dalla forza magnetica, infatti, è nullo.
Forza magnetica e lavoro
La forza magnetica non compie mai lavoro. Infatti,
ΔL=𝑭 ∙ 𝚫𝐬 ma, poiché 𝚫𝐬//𝒗 e 𝑭┴𝒗 , il prodotto scalare è nullo e, quindi, ΔL=0.
In base al teorema dell’energia cinetica, Kb-Ka=Lab.
Poiché il lavoro è sempre nullo, segue che la forza magnetica non varia mai l’energia cinetica della
particella.
In altri termini, se una particella si muove sotto l’azione della sola forza magnetica, non può cambiare il
modulo della sua velocità, ma solo la direzione del moto.
Espressione generale della forza di Lorentz
Consideriamo una carica q che si muove con velocità 𝑣 sottoposta all’effetto di un campo elettrico 𝐸 e
un campo magnetico 𝐵. La particella risente di una forza totale definita dalla seguente legge:
𝑭 = 𝒒(𝑬 + 𝒗×𝑩)
Unità di misura di 𝑩
[B]= [B]=
[!]
!
!
!
∙
!
!
=T
La lettera T indica il Tesla, che è un’unità di misura del S.I.
L’esperimento di Thomson
Thomson utilizzò per i sui esperimenti un tubo di vetro dal quale fu rimossa tutta l’aria, chiamato tubo
catodico, al cui interno era presente un cannoncino elettronico, cioè un dispositivo formato da un
filamento metallico che, surriscaldato, emette elettroni, e da una griglia di accelerazione grazie alla
quale gli elettroni acquistano energia cinetica. Dal cannoncino elettronico parte un fascio di elettroni che
viene sottoposto all’azione di un campo elettrico.
Cannoncino elettronico Il fascio di elettroni sarà deviato di un angolo θ rispetto alla sua traiettoria rettilinea.
𝒕𝒈𝜽 =
𝒆𝑬𝒍
𝟐𝒎𝒗𝟐𝟎
!
Per misurare è necessario conoscere 𝒗𝟎 . A questo scopo, Thomson introdusse un campo magnetico 𝐵
!
tale da riportare gli elettroni su una traiettoria rettilinea. Si ha dunque:
𝑭𝒕𝒐𝒕 = 𝒒(𝑬 + 𝒗₀×𝑩)
0 = 𝒒(𝑬 + 𝒗₀×𝑩)
𝑬 = −𝒗₀× 𝑩
il vettore 𝐵 deve essere scelto perpendicolare al piano contenente 𝑣! e 𝐸.
Il modulo di 𝐸 è:
𝑬 = 𝒗₀𝑩 Poiché 𝐸 e 𝐵 sono noti sperimentalmente, è possibile calcolare la velocità della particella:
𝑬
𝒗₀ =
𝑩
!
Sostituendo 𝒗₀ si ricava l’espressione finale di in termini di grandezze note sperimentalmente:
!
𝒆
𝒕𝒈𝜽 𝑬 =
𝒎
𝑩𝟐 𝒍
Con questo esperimento Thomson ricavò la prima valutazione carica/massa dell’elettrone e riuscì a
capire che si trattava di particelle molto leggere aventi carica negativa. Il fisico Millikan, con i suoi
esperimenti, riuscì a calcolare separatamente la carica e la massa dell’elettrone.
L’effetto Hall.
Consideriamo una lastrina percorsa da una densità di corrente 𝐽. Applichiamo un campo magnetico 𝐵 e
studiamo l’effetto di tale campo sulle cariche.
Le cariche subiscono l’effetto della forza di Lorentz 𝐹! = 𝑞𝑣×𝐵. Occorre distinguere due casi:
•
Portatori di carica positivi
Le cariche che entrano nella lastrina sono deflesse verso il basso con un conseguente accumulo
di cariche negative nella parte superiore. Ciò determina il formarsi di un campo elettrico 𝐸 e di
una forza elettrica 𝐹! che controbilancia 𝐹! .
Fm = Fe
qvB = qE vB = E
Poiché c’è un campo elettrico trasversale ad 𝐸, c’è una differenza di potenziale VH = EL = vBL
V = !
!"
𝑉! = !"#
!"
L’unica incognita di questa equazione è n, poiché tutte le altre grandezze sono misurabili
sperimentalmente. Calcolando le differenze di potenziale possiamo stimare il numero di
portatori di carica n.
•
Portatori di carica negativi
La forza magnetica 𝐹! è diretta verso il basso poiché q<0.
Diversamente da quanto accaduto nel primo caso, abbiamo un accumulo di cariche negative
nella parte bassa della lastrina.
L’effetto Hall permette, quindi, di discriminare il segno dei portatori di carica. Ricordiamo, inoltre, che
nell’effetto Hall non c’è potenza dissipata, in quanto:
•
•
La forza magnetica 𝐹! non compie mai lavoro.
Il campo elettrico 𝐸 è traversale alla velocità 𝑣 a regime. La forza elettrica 𝐹! associata al
campo elettrico 𝐸 è, di conseguenza, anch’essa perpendicolare a 𝑣. Essa, quindi, non compie
lavoro.
Dinamica di una carica in presenza di un campo magnetico
Consideriamo il caso di una carica positiva q che entra in una regione in cui è presente un campo
magnetico uniforme (fig.2) con il vettore della velocità iniziale 𝒗₀ della carica perpendicolare al campo.
Assumiamo che il verso del campo magnetico sia uscente dal piano (fig.2).
q Fig.2 La carica si muove di moto circolare uniforme perché la forza magnetica 𝐹! , perpendicolare a 𝑣
(velocità della carica), si comporta come una forza centripeta.
Per la seconda legge di Newton:
𝐹!"! = m𝑎
Notiamo che in direzione tangenziale non agisce nessuna forza e, di conseguenza, la velocità è costante
in modulo. In direzione centripeta, invece, agisce la forza 𝐹! . Possiamo, quindi, scrivere
qvB = mac
dove ac è l’accelerazione centripeta
𝐯𝟐
ac = = ωv
𝐫
sostituendo ac nell’equazione precedente, otteniamo:
qB = mω
da cui possiamo ricavare la pulsazione di ciclotrone ω:
ω = 𝐪𝐁
𝐦
È importante considerare che ω non dipende dalla velocità della particella, ma soltanto dalla carica ,
dalla massa e dal campo magnetico. Questo significa che, se osserviamo due particelle cariche uguali
aventi velocità diverse che entrano nella regione in cui è presente il campo magnetico B, esse usciranno
fuori dal campo magnetico nello stesso istante perché il tempo impiegato per percorrere una
semicirconferenza è legato alla velocità angolare ω.
Il raggio della semicirconferenza dipende, invece, dalla velocità della carica
v = ωr
r=
𝐯
𝛚
=
𝐦𝐯
𝐪𝐁
Moto elicoidale
Se una carica, avente il vettore velocità che forma un angolo diverso da quello retto con 𝐵, si muove in
un campo magnetico uniforme, il suo percorso è un’elica.
Possiamo verificare questa affermazione in base alla seconda legge di Newton, proiettando l’equazione
Ftot = ma su tre assi; otteniamo così tre equazioni:
𝟎 = 𝒎𝒂𝒕
𝒒𝒗𝑩𝒔𝒆𝒏𝜽 = 𝒎𝒂𝒄
𝟎 = 𝒎𝒂𝒙
Questo moto elicoidale è una composizione di due moti, quello rettilineo uniforme in direzione dell’asse
x e quello circolare uniforme nel piano yz.
Le equazioni parametriche sono:
r = cost
θ = ωt
x = v xt
Notiamo che le particelle cariche si muovono seguendo eliche che si avvolgono intorno alle linee di
campo magnetico e che le particelle aventi carica negativa ruoteranno in senso opposto rispetto alle
particelle con carica positiva.
Bottiglia magnetica e aurore boreali
Quando una carica si muove in un campo magnetico non
uniforme, il moto è più complesso. Per esempio, in un campo
magnetico che è forte agli estremi e debole al centro, la
carica può oscillare avanti ed indietro tra gli estremi. Una
carica posta ad un estremo compie una spirale lungo le linee
di campo fino a che non raggiunge l'estremo opposto, dove
inverte il suo percorso e compie una spirale inversa. Questa
configurazione è nota come bottiglia magnetica, poiché le
cariche possono venire intrappolate al suo interno. La
bottiglia magnetica è usata come barriera per intrappolare
i plasmi e gioca un ruolo cruciale nel controllo della fusione
nucleare.
Le particelle, intrappolate dal campo magnetico non
uniforme terrestre, compiono una spirale intorno alle
linee di campo da polo a polo, coprendo la distanza in
qualche secondo. Queste particelle sono originate in
maggior parte dal Sole. Per questa ragione il flusso di
tale cariche è conosciuto come “vento solare”. La
maggior parte delle particelle che fanno parte del vento
solare vengono deviate dal campo magnetico terrestre e
non raggiungono l'atmosfera. Tuttavia, alcune cariche
vengono catturate; quando le particelle si trovano ai
poli, qualche volta collidono con gli atomi presenti
nell'atmosfera, causando l'emissione da parte di questi
ultimi di luce visibile. Collisioni come questa originano
le Aurore Boreali (nell'emisfero settentrionale) e le Aurore Australi (nell'emisfero meridionale).
Lo spettrometro di massa.
Uno spettrometro di massa è uno strumento che separa gli ioni secondo il loro rapporto massa/carica. In
questo modo è possibile riconoscere un materiale ignoto. Il materiale oggetto di studio viene ionizzato e
vaporizzato. Il fascio di ioni che si ottiene entra in una regione con campo magnetico uniforme 𝐵. A
causa della forza magnetica che agisce su di essi, gli ioni percorrono traiettorie semicircolari per poi
urtare una lastra fotografica che resterà impressionata in un certo punto a seconda del tipo di ioni che
compone il fascio. Questa descrizione corrisponde al funzionamento del primo spettrometro di massa,
ideato e realizzato dal fisico Demster.
q 𝐵 𝒗𝟎 Lastra fotografica Conoscendo il raggio r della semicirconferenza percorsa dagli ioni
r=
𝒎𝒗𝟎
𝒒𝑩
possiamo capire di che ione si tratta determinando il loro rapporto
𝒎
𝒒
=
𝒓𝑩
𝒗𝟎
.
Il campo magnetico 𝐵! e il raggio r sono noti sperimentalmente, occorre quindi determinare 𝑣! . Una
tecnica per determinare 𝑣! è quella di preparare un fascio di ioni con un cannoncino elettronico. Grazie
alla griglia di accelerazione del cannoncino elettronico determiniamo l’energia cinetica degli ioni del
𝟏
fascio 𝒎𝒗𝟐𝟎 = 𝒒∆𝑽 da cui possiamo ricavare:
𝟐
𝒗𝟐𝟎 =
𝟐𝒒∆𝑽
𝒗𝟎 =
𝒎
𝟐𝒒∆𝑽
𝒎
Sostituendo 𝒗𝟎 otteniamo: 𝒎
𝒒
= 𝑟𝐵
!!
!!
𝒎
𝒒
𝒎
𝟐𝒒∆𝑽
= 𝑟 ! 𝐵 !
= 𝒎
𝟐𝒒∆𝑽
! !!!
𝟐∆𝑽
Con questa tecnica il rapporto massa/carica è determinato con un’equazione non lineare; per ottenere
un’equazione lineare occorre utilizzare un selettore di velocità.
Il selettore di velocità è uno strumento che determina la velocità delle particelle. È costituito da un
campo elettrico uniforme, generato da un condensatore a facce piane e parallele, e da un campo
magnetico uniforme perpendicolare al campo elettrico, in cui viene fatto passare un fascio di particele
cariche. Se si scelgono in modo opportuno il campo elettrico e il campo magnetico, in modo che la forza
totale 𝑭𝒕𝒐𝒕 = 𝒒 𝑬 + 𝒗𝟎 ×𝑩𝟎 che agisce sulle particelle sia nulla, il fascio di particelle si muoverà lungo
una traiettoria rettilinea. Conoscendo 𝑬 e 𝑩𝟎 otteniamo il valore della velocità 𝒗𝟎
𝒗𝟎 =
𝑬
𝑩𝟎
𝐵 𝒗𝟎 𝐸 𝑆𝑒𝑙𝑒𝑡𝑡𝑜𝑟𝑒 𝑑𝑖 𝑣𝑒𝑙𝑜𝑐𝑖𝑡à 𝑩𝟎 Sostituendo 𝒗𝟎 nell’equazione
𝒎
𝒒
=
𝒓𝑩
𝒗𝟎
otteniamo il rapporto massa/carica espresso con un’equazione
lineare
𝒎 𝒓𝑩𝟎 𝑩
=
𝒒
𝑬
Forza di Laplace
Consideriamo una sezione di filo percorsa da corrente. Su di essa agisce una forza magnetica
complessiva ∆𝐹 che prende il nome di forza di forza di Laplace.
Su una sola carica abbiamo la forza magnetica:
𝑭𝒎 = q𝒗×𝑩
Su ΔN cariche avremo, invece, la forza magnetica totale:
∆𝑭 = ΔNq𝒗×𝑩
Indicando con n il numero di cariche per unità di volume,
troviamo:
ΔN = nΣΔl
La forza totale ∆𝐹 sarà:
∆𝑭 = nΣΔl q𝒗×𝑩
Poiché il prodotto nq𝑣 è la densità di corrente 𝐽, possiamo scrivere:
∆𝑭 = ΣΔl 𝑱×𝑩
Da questa espressione possiamo ricavare la formula della forza per unità di volume, sapendo che
ΔV=ΣΔl:
∆𝑭/ΔV = 𝑱×𝑩
Considerando ora che ∆𝑙 // 𝐽, possiamo riscrivere la formula:
∆𝑭 = Σ Δl 𝑱×𝑩
∆𝑭 = Σ J ∆𝒍 × 𝑩
Infine, essendo l’intensità di corrente i = ΣJ, otteniamo:
∆𝑭 = i ∆𝒍 ×𝑩
Forza totale su un circuito percorso da corrente
Consideriamo un circuito immerso in un campo magnetico 𝐵 e calcoliamo la forza totale Ftot che agisce
su di esso:
𝐹!"! = ! Δ F!
Se B è uniforme allora Ftot=0
𝐹!"! = ! i ΔSk
x 𝐵=i(
ma in un circuito chiuso
! ΔSk)x
𝐵
! ΔSk =
0 e, di conseguenza, 𝐹!"! = 0.
𝛥𝑠 Consideriamo, ora, un circuito rettangolare immerso in un campo magnetico 𝐵.
𝛥𝐹! . 𝛥𝐹! . 𝛥𝐹! . 𝐹!"! = ! ∆𝐹! =
0
Nonostante 𝐹!"! = 0, le singole forze ∆𝐹! tendono a stirare il circuito.
Per questo motivo, se il circuito non è rigido, esso si deformerà.
𝛥𝐹! . 𝐵 𝛥𝐹! . 𝛥𝐹! . Per avere una forza netta 𝐹!"! ≠ 0 sul circuito, occorre immergerlo
in un campo magnetico non uniforme.
Sul circuito agirà una forza netta 𝐹!"! = ∆𝐹! .
𝛥𝐹! . Momento magnetico
Un circuito rettangolare percorso da corrente immerso in un campo magnetico 𝐵 e che forma un angolo
θ con la normale al circuito 𝑛 (che si determina stabilendo il verso di percorrenza positivo della corrente
e utilizzando la regola della mano destra), subisce un momento torcente 𝝉: Δs2 𝐹 2 𝐹 1 𝐵 𝑖 𝑛 𝐹 3 Δs1 Δs3 𝐹 4 Δs4 Le forze 𝐹 2 e 𝐹 4 sono uguali in modulo e hanno stessa direzione, ma verso opposto e, quindi, non hanno
alcun effetto; anche le forze 𝐹 1 e 𝐹 3 sono uguali ed opposte. Ne segue che la forza totale 𝐹!"! che
agisce sul circuito è nulla. Le forze 𝐹 1 e 𝐹 3, però, agiscono su due rette parallele formando una coppia di
forze di cui si può misurare il momento meccanico totale 𝜏 tot, dato dal prodotto tra la forza F1 ed il
braccio b.
𝑛 𝝉𝒕𝒐𝒕 = 𝒃𝑭𝟏 Poiché F1 = iΔs1B:
𝝉𝒕𝒐𝒕 = 𝒃 𝒊 𝜟𝒔𝟏 𝑩 Il braccio b vale:
𝒃 = 𝜟𝒔𝟐 𝒔𝒆𝒏𝜽 Sostituendo ricaviamo l’equazione:
𝝉𝒕𝒐𝒕 = 𝒊 𝜟𝒔𝟏 𝑩 𝜟𝒔𝟐 𝒔𝒆𝒏𝜽 Il prodotto Δs2 Δs1 corrisponde all’area Σ del rettangolo.
Definiamo il momento magnetico m come il prodotto tra l’intensità di corrente i e l’area del circuito Σ:
𝒎 = 𝒊𝜮 Quindi possiamo scrivere τ in relazione al momento magnetico:
𝝉 = 𝒎𝑩𝒔𝒆𝒏𝜽 Questa formula può essere scritta sotto forma di prodotto vettoriale:
𝝉 = 𝒎×𝑩
definendo il vettore 𝒎 come:
𝒎=iΣ𝑛
Il momento magnetico di un circuito di forma qualsiasi si calcola in questo modo:
𝑛 𝑛 Dividiamo la superficie del circuito in piccole parti. Possiamo, così, calcolare il momento magnetico di
ciascuna parte:
𝒎k = ik ΔΣk 𝑛
Il momento magnetico totale 𝒎tot è uguale alla somma dei momenti magnetici 𝒎k:
𝒎tot =
𝒌 𝒎𝒌