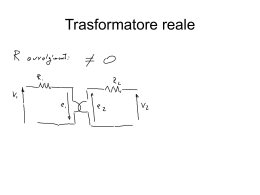
MODELLIZZAZIONE DI UNA LINEA
ELETTRICA
Appunti a cura dell’Ing. Emanuela Pazzola
Tutore del corso di Elettrotecnica per meccanici, chimici e
biomedici
A.A. 2005/2006
Facoltà d’Ingegneria dell’Università degli Studi di Cagliari
CAPITOLO 5. MODELLIZZAZIONE DI UNA LINEA ELETTRICA
5.1 Circuito equivalente di una linea elettrica
pag. 2
5.2 Calcolo della caduta di tensione di linee elettriche
corte
pag. 8
5.3 Caduta di tensione in una linea che alimenta un
carico Ohmico-Induttivo
pag. 9
5.4 Caduta di tensione in una linea che alimenta un
carico puramente ohmico pag. 10
pag. 10
5.5 Caduta di tensione in una linea che alimenta un
carico ohmico-capacitivo
pag. 11
5.6 Calcolo della Caduta di Tensione %
pag. 13
1
CAPITOLO 5
MODELLIZZAZIONE DI UNA LINEA ELETTRICA
5.1 Circuito equivalente di una linea elettrica
In questo capitolo verrà esaminato il comportamento elettrico delle linee
elettriche e la loro modellizzazione, intesa come rappresentazione del circuito
equivalente.
Una linea elettrica può essere considerata come un doppio bipolo con
differenti valori di tensione e corrente tra i morsetti 1-1’ a monte e 2-2’ a valle della
linea.
Fig. 1 Rappresentazione di una linea elettrica come doppio bipolo
Per simulare la variazione di tensione e corrente fra i morsetti a monte ed a valle
di una linea elettrica, si introducono le seguenti grandezze:
•
L’impedenza longitudinale Z = R + jX
•
L’ammettenza trasversale Y = G + jB
Il quadripolo può dunque essere quindi rappresentato nel modo seguente:
2
Fig. 2 Circuito equivalente di una linea elettrica
Dove:
•
R rappresenta la resistenza ohmica dei conduttori di linea;
•
X rappresenta la reattanza dovuta alla f.e.m. di autoinduzione che si
genera nel circuito elettrico quando questo è attraversato da una
corrente di valore unitario;
•
G rappresenta la conduttanza della linea, dovuta al fatto che lungo il
percorso del conduttore di linea la corrente si irradia lungo lo spazio
circostante, attraverso gli isolatori o mediante una ionizzazione
dell’aria, fenomeno meglio conosciuto come effetto Corona.
•
B rappresenta la suscettanza della linea, dovuta alla capacità del
conduttore verso terra e verso gli altri conduttori.
Tali grandezze sono generalmente riferite all’unità di lunghezza (1 km), in
tal caso si parla di costanti fondamentali della linea:
•
Ω
Resistenza (r) e reattanza chilometrica(x) della linea   ;
 km 
•
 S 
Conduttanza (g) e suscettanza (b) chilometrica della linea   .
 km 
Lo studio delle linee trifasi è riconducibile a quello delle linee monofasi,
utilizzando lo stesso quadripolo.
Poiché la variazione della tensione e della corrente si verificano in ciascun
tratto elementare dλ di linea (fig. 3), la valutazione rigorosa di queste grandezze
richiede un circuito a parametri distribuiti, caratterizzato dalle seguenti equazioni:
3
∂i

di = − gud λ − c ∂t d λ

du = − rid λ − I ∂i d λ
∂t

(1)
Fig. 3 Tratto elementare di linea
Dividendo le espressioni precedenti per dλ, derivando rispetto a λ e
sostituendo opportunamente le variabili, si ricavano le note equazioni dei
telegrafisti:
 ∂ 2u
∂u
∂ 2u
rgu
(
rc
Ig
)
Ic
dλ
=
+
+
+
 2
∂t
∂λ
∂t 2
 2
2
 ∂ i = rgi + (rc + Ig ) ∂i + Ic ∂ i
 ∂t 2
∂t
∂t 2
(2)
Si tratta di equazioni differenziali del II ordine a derivate parziali
perfettamente analoghe. Ciò è indice del fatto che la propagazione della tensione
e corrente lungo la linea avviene allo stesso modo.
La modellizzazione di un tratto di linea infinitesimo simmetrico dλ si ottiene
dimezzando l’impedenza longitudinale in due parti:
4
Fig. 4 Circuito equivalente di un tratto di linea di lunghezza infinitesima dλ
Nel caso di regime permanente sinusoidale si definisce lunghezza d’onda λ della
linea, la distanza che intercorre lungo la linea tra due massimi successivi della
tensione e della corrente. L’espressione approssimata di λ è la seguente:
λ=
In cui v =
1
µε
2π
ω µε
==
1
f µε
=
v
essendo v =
f
1
µε
(3)
corrisponde alla velocità di propagazione nel mezzo caratterizzato
dai relativi valori di µ e di ε.
Si analizzino i seguenti due casi:
•
H 
F 
Linea in aria ( µ 0 = 4π • 10 −7  ; ε 0 = 8.856 • 10 −12   ), interessata da
m
m
tensione e corrente di frequenza pari a 50 Hz.
La lunghezza d’onda in questa situazione assumerà il valore λ=6000 km,
come risulta applicando la (3).
Nell’istante t in cui il valore di tensione u(t) risulta pari a 0, la distribuzione
della tensione sarà la seguente:
5
Fig. 5 Distribuzione della tensione per linee in aria nell’istante t in cui u(t) = 0
•
Linea in cavo con costante dielettrica relativa εr=2,3 interessata da
tensione e corrente di frequenza pari a 50 Hz.
La corrispondente lunghezza d’onda assumerà il valore λ=4000 km.
Nell’istante t in cui il valore di tensione u(t) risulta pari a 0, pertanto la
distribuzione della tensione assumerà la forma seguente:
Fig. 6 Distribuzione della tensione per linee in cavo nell’istante t in cui u(t)=0
Il confronto fra i diagrammi dell figg. 5 e 6 mostra dunque come la tensione lungo
un tratto di linea sia variabile da punto a punto.
Inoltre, in uno stesso tratto di linea ∆λ, la caduta di tensione aumenta al crescere
della tensione di alimentazione della linea, come mostra il diagramma seguente,
ottenuto per tensioni pari a 220 kV e 130 kV:
6
Fig. 7 Confronto fra la distribuzione della tensione nelle linee in aria ed in quelle in cavo
Per tali ragioni, in regime sinusoidale permanente (f=50 Hz), le linee aventi
lunghezza inferiore a 150 km e tensione inferiore a 130 kV possono approssimarsi
mediante quadripoli equivalenti a T (fig. 8) o a π (fig. 9), a parametri concentrati.
Fig. 8 Quadripolo equivalente a T
Fig. 9 Quadripolo equivalente a π
Per linee cosiddette “corte” (lunghezza < 60 km), il modello circuitale può
ulteriormente semplificarsi; infatti, essendo l‘entità dell’assorbimento di corrente
7
molto piccola, sono trascurabili i parametri trasversali, così come illustrato dalla
fig. 10.
Fig. 10 Circuito equivalente per linee “corte”
5.2 Calcolo della caduta di tensione di linee elettriche corte
Data la linea elettrica corta, schematizzata in fig. 10, noti i fasori della tensione
( U 2 ) e della corrente ( I ), ci si propone di determinare le grandezze di ingresso
( U 1 , φ1).
Il corrispondente diagramma è rappresentato in fig. 11.
Fig. 11 Diagramma fasoriale relativo al circuito di fig. 8
2
2
U 1 = OF = OH + HF
(4)
OH = OG + GH = U 2 cos ϕ 2 + RL I
(5)
HF = HE + EF = U 2 senϕ 2 + X L I
(6)
8
Le espressioni esatte di U1e φ1 saranno:
U 1 = (U 2 cos ϕ + R L I ) 2 + (U 2 senϕ + X L I ) 2
(7)
§ HF ·
§ U senϕ 2 + X L I ·
¸ = arctg ¨¨ 2
¸¸
ϕ1 = arctg ¨¨
¸
cos
ϕ
+
U
R
I
OH
2
L ¹
© 2
¹
©
(8)
Si definisce caduta di tensione in linea, la differenza fra il valore efficace della
tensione in ingresso e di quella in uscita dalla linea:
∆U = U 1 − U 2 = OF − OA = OD − OA = AD
(9)
Poiché l’angolo φ è piccolo può ritenersi valida la seguente approssimazione:
∆U = AD ≈ AC = AB + BC = RL I cos ϕ 2 + X L Isenϕ = ( RL cosϕ 2 + X L senϕ 2 ) I
(10)
5.3 Caduta di tensione in una linea che alimenta un carico
Ohmico-Induttivo
Nell’ipotesi che una linea alimenti un carico ohmico – induttivo (R+jX), il
circuito diviene come indicato in figura:
Fig. 12 Circuito equivalente di una linea corta che alimenta un carico ohmico-induttivo
Il relativo diagramma fasoriale è indicato in fig. 13, in cui:
•
I2 rappresenta la corrente che attraversa il carico;
•
φ2 rappresenta la fase della corrente (nonché lo sfasamento fra tensione e
corrente).
9
Fig. 13 Diagramma fasoriale relativo al circuito di fig. 12
Essendo la fase φ2 <0, la (10) diventa:
∆U = RL I cos ϕ 2 + X L Isenϕ > 0
5.4 Caduta di tensione in una linea che alimenta un carico
puramente ohmico
Nell’ipotesi che la linea alimenti un carico puramente ohmico (R-jX), il
circuito diviene come indicato in figura:
Fig. 14 Circuito equivalente di una linea corta che alimenta un carico puramente ohmico
Il corrispondente diagramma fasoriale è rappresentato in fig. 15.
10
Fig. 15 Diagramma fasoriale relativo al circuito di fig. 14
In questo caso, essendo la fase φ2 =0, la (10) diventa:
∆U = RL I cos ϕ 2
5.5 Caduta di tensione in una linea che alimenta un carico
ohmico-capacitivo
Nell’ipotesi che la linea alimenti un carico ohmico – capacitivo (R – j XL), il
circuito diviene il seguente:
Fig. 16 Circuito equivalente di una linea corta che alimenta un carico ohmico-capacitivo
In cui:
•
I2 rappresenta la corrente che attraversa il carico;
•
φ2 rappresenta la fase della corrente (nonché lo sfasamento fra tensione e
corrente).
11
Essendo la fase φ2>0, possono verificarsi le seguenti situazioni:
• φ2=φ*
Sostituendo nella (10) si ottiene:
∆U = RL I cos ϕ * + X L Isenϕ * = 0
Il valore della tensione in arrivo è uguale al valore della tensione in partenza.
• φ2<φ*
Sostituendo nella (10) si ottiene:
∆U = RL I cos ϕ * + X L Isenϕ * > 0
Il valore della tensione in arrivo è minore rispetto al valore della tensione in
partenza.
Fig. 17 Diagramma fasoriale relativo al circuito di fig. 16
• φ2>φ*
Sostituendo nella (10) si ottiene:
∆U = RL I cos ϕ 2 + X L Isenϕ 2 < 0
Il valore della tensione in arrivo è maggiore rispetto al valore della tensione in
partenza.
12
5.6 Calcolo della Caduta di Tensione %
Moltiplicando e dividendo l’espressione della caduta di tensione per la tensione
all’arrivo della linea (U2), si ottiene la seguente:
∆U =
R L (IU 2 cos ϕ ) + X L ( IU 2 senϕ ) R L P + X L Q
=
U2
U2
(11)
In cui:
•
RL
ed
XL
rappresentano
la
resistenza
e
reattanza
della
linea,
rispettivamente;
•
P e Q rappresentano la potenza attiva e reattiva assorbite dal carico (Si
ricorda: P=UIcosφ e Q=UIsenφ).
Definiamo caduta di tensione percentuale la seguente:
∆U % =
R P + X LQ
∆U
100 = L
100
2
U2
U2
(12)
13