I numeri e la loro rappresentazione, le frazioni
Saeli Donato
26 marzo 2015
“Al mondo ci sono tre tipi di persone: quelle che sanno contare
e quelle che non sanno contare.”
Ian Stewart
Nell’osso sono state intagliate 55 tacche, a gruppi di 5.
Le prime 25 tacche sono separate dalle altre da una tacca
di lunghezza doppia.
Nell’osso sono state intagliate 55 tacche, a gruppi di 5.
Le prime 25 tacche sono separate dalle altre da una tacca
di lunghezza doppia.
Anche se non sappiamo in che modo siano state prodotte
queste tacche, la spiegazione più plausibile è che un uomo
preistorico l’abbia fatto deliberatamente.
Forse stava
registrando il numero di un insieme, probabilmente di pelli,
o di familiari, o di giorni trascorsi da un determinato evento.
È ragionevole supporre che egli facesse una tacca per ogni
oggetto appartenente all’insieme che stava considerando.
“Le donne porgevano un pezzo di legno, lungo una ventina
di centimetri, segnato da tratti di lima. Ogni pezzo era diverso,
alcuni ricavati da rami, altri quadrati e piallati. Il fornaio ne
aveva il duplicato infilati in una cinghia di cuoio. Egli cercava
il nome segnato in cima ai suoi legni, lo confrontava con quello
del cliente; le tacche corrispondevano esattamente”. Allora si
poteva saldare il conto del pane preso a credito. Cosı̀ accadeva
ancora nel 1869 in Francia dalle parti di Saint-Étienne, ...
“Le donne porgevano un pezzo di legno, lungo una ventina
di centimetri, segnato da tratti di lima. Ogni pezzo era diverso,
alcuni ricavati da rami, altri quadrati e piallati. Il fornaio ne
aveva il duplicato infilati in una cinghia di cuoio. Egli cercava
il nome segnato in cima ai suoi legni, lo confrontava con quello
del cliente; le tacche corrispondevano esattamente”. Allora si
poteva saldare il conto del pane preso a credito. Cosı̀ accadeva
ancora nel 1869 in Francia dalle parti di Saint-Étienne, ...
Incidere tacche, che si trattasse di ossa ritrovate in caverne
del paleolitico, di bastoncini di fornai francesi o degli “stocks”
della Corte dello Scacchiere inglese, è stato per decine
di migliaia di anni il modo di tenere i conti, finché nell’Ottocento
un incendio epocale ha ridotto in Cenere, insieme agli “stocks”,
l’intero Parlamento inglese.
[Bo, 27]
S. Kubrick 2001: Odissea nello spazio - 1968
I sistemi posizionali più quotati
base
2
8
10
12
16
cifre
0, 1
0, 1, 2, 3, 4, 5, 6, 7
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
X, E
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
a, b, c, d, e, f
denominazione
binario
ottale
decimale
duodecimale
esadecimale
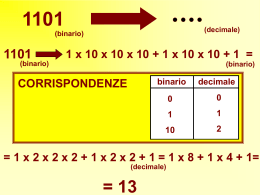
Nella tabella seguente i primi 16 numeri naturali vengono
rappresentati in tutti questi sistemi.
binario
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
v
ottale
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
decimale
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
duodecimale
0
1
2
3
4
5
6
7
8
9
X
E
10
11
12
13
esadecimale
0
1
2
3
4
5
6
7
8
9
a
b
c
d
e
f
Esempio
Consideriamo la sequenza di cifre 101312 in base 12. •
In questo sistema, le posizioni successive rappresentano
potenze di 12; cosı̀
3
2
1
101312 = 1 · 12 + 0 · 12 + 1 · 12 + 3 = 1728 + 12 + 3 = 1743.
•
La base usata nella rappresentazione di un numero viene specificata
con un indice; conveniamo di omettere l’indicazione della base nel caso
di rappresentazioni decimali.
Esempio
Consideriamo la sequenza di cifre 101312 in base 12. •
In questo sistema, le posizioni successive rappresentano
potenze di 12; cosı̀
3
2
1
101312 = 1 · 12 + 0 · 12 + 1 · 12 + 3 = 1728 + 12 + 3 = 1743.
Per rappresentare questo stesso numero in base 16
eseguiamone la divisione euclidea per 16; otteniamo
1743 = 16 · 108 + 15. Dividiamo ora 108 per 16, abbiamo
108 = 16 · 6 + 12, finalmente impiegando questa relazione
nella precedente
2
1743 = 16 · (16 · 6 + 12) + 15 = 6 · 16 + 12 · 16 + 15 = 6cf16 .
•
La base usata nella rappresentazione di un numero viene specificata
con un indice; conveniamo di omettere l’indicazione della base nel caso
di rappresentazioni decimali.
Esempio
Consideriamo la sequenza di cifre 101312 in base 12. •
In questo sistema, le posizioni successive rappresentano
potenze di 12; cosı̀
3
2
1
101312 = 1 · 12 + 0 · 12 + 1 · 12 + 3 = 1728 + 12 + 3 = 1743.
Per rappresentare questo stesso numero in base 16
eseguiamone la divisione euclidea per 16; otteniamo
1743 = 16 · 108 + 15. Dividiamo ora 108 per 16, abbiamo
108 = 16 · 6 + 12, finalmente impiegando questa relazione
nella precedente
2
1743 = 16 · (16 · 6 + 12) + 15 = 6 · 16 + 12 · 16 + 15 = 6cf16 .
Rappresentiamo ora lo stesso numero in base 8.
1743 = 8 · 217 + 7,
217 = 8 · 27 + 1,
27 = 8 · 3 + 3;
pertanto 1743 = 33178 .
•
È:
La base usata nella rappresentazione di un numero viene specificata
con un indice; conveniamo di omettere l’indicazione della base nel caso
di rappresentazioni decimali.
Rappresentiamo infine ancora lo stesso numero in base 2.
Abbiamo:
1743 = 2 · 871 + 1,
871 = 2 · 435 + 1,
435 = 2 · 217 + 1,
217 = 2 · 108 + 1,
108 = 2 · 54 + 0,
54 = 2 · 27 + 0,
27 = 2 · 13 + 1,
13 = 2 · 6 + 1,
6 = 2 · 3 + 0,
3 = 2 · 1 + 1;
dunque 1743 = 110110011112 .
Senza parole
ottale
3
3
1
7
z }|
{ z }|
{ z }|
{ z }|
{
011011001111
binario
0
| 1{z1 1}
| 1{z1 0} 1
| 1{z0 0} 1
6
c
f
esadecimale
r
Operazioni
Quale che che sia la base le operazioni si effettuano come
nel sistema decimale, ma ....
Operazioni
Quale che che sia la base le operazioni si effettuano come
nel sistema decimale, ma .... occorre imparare le tabelle.
Operazioni
Quale che che sia la base le operazioni si effettuano come
nel sistema decimale, ma .... occorre imparare le tabelle.
In binario tutto è relativamente facile, basta solo ricordare
che 1 + 1 fa 102 . (Ma forse anche che 112 + 1 = 1002 ,
1112 + 1 = 10002 , 11112 + 1 = 100002 , ...)
Operazioni
Quale che che sia la base le operazioni si effettuano come
nel sistema decimale, ma .... occorre imparare le tabelle.
In binario tutto è relativamente facile, basta solo ricordare
che 1 + 1 fa 102 . (Ma forse anche che 112 + 1 = 1002 ,
1112 + 1 = 10002 , 11112 + 1 = 100002 , ...)
Sommiamo 111101012 = 245 e 1001111002 = 316, abbiamo:
˙ ˙ 1̇1̇1̇1̇0̇101 +
100111100 =
10001100012
I puntini sulle cifre del primo addendo indicano il riporto di 1.
La moltiplicazione è più laboriosa a causa dei riporti,
anche a più cifre, nell’addizione dei prodotti parziali:
11110101 ×
100111100 =
˙ ˙ ˙ ˙˙ ˙ ˙ 1̇11̇1̇0̇10100
11110101
11110101
11110101
1111010100
100101110011011002
Tavola “pitagorica” in ottale:
×
2
3
4
5
6
7
2
4
6
10
12
14
16
3
6
11
14
17
22
25
4
10
14
20
24
30
34
5
12
17
24
31
36
43
6
14
22
30
36
44
52
7
16
25
34
43
52
61
Tavola “pitagorica” in ottale:
×
2
3
4
5
6
7
2
4
6
10
12
14
16
3
6
11
14
17
22
25
4
10
14
20
24
30
34
5
12
17
24
31
36
43
6
14
22
30
36
44
52
Moltiplichiamo 3658 = 245 per 4748 = 316 :
365 ×
474 =
1724
3263
1724
2271548
7
16
25
34
43
52
61
Tabella di moltiplicazione in base sedici:
×
2
3
4
5
6
7
8
9
a
b
c
d
e
f
2
4
6
8
a
c
e
10
12
14
16
18
1a
1c
1e
3
6
9
c
f
12
15
18
1b
1e
21
24
27
2a
2d
4
8
c
10
14
18
1c
20
24
28
2c
30
34
38
3c
5
a
f
14
19
1e
23
28
2d
32
37
3c
41
46
4b
6
c
12
18
1e
24
2a
30
36
3c
42
48
4e
54
5a
7
e
15
1c
23
2a
31
38
3f
46
4d
54
5b
62
69
8
10
18
20
28
30
38
40
48
50
58
60
68
70
78
9
12
1b
24
2d
36
3f
48
51
5a
63
6c
75
7e
87
a
14
1e
28
32
3c
46
50
5a
64
6e
78
82
8c
96
b
16
21
2c
37
42
4d
58
63
6e
79
84
8f
9a
a5
c
18
24
30
3c
48
54
60
6c
78
84
90
9c
a8
b4
d
1a
27
34
41
4e
5b
68
75
82
8f
9c
a9
b6
c3
e
1c
2a
38
46
54
62
70
7e
8c
9a
a8
b6
c4
d2
f
1e
2d
3c
4b
5a
69
78
87
96
a5
b4
c3
d2
e1
La medesima moltiplicazione eseguita in base 16
f5×
13c =
b7c
2d f
f5
12e6c16
La medesima moltiplicazione eseguita in base 16
f5×
13c =
b7c
2d f
f5
12e6c16
ed infine, in base 10
245 ×
316 =
1470
245
735
77420
Ufficialmente, il primo ad esporre una trattazione sistematica
dei sistemi di numerazione posizionali fu il matematico tedesco
G. W. Leibniz; anche se l’inglese T. Harriot ne aveva discusso
e scritto oltre mezzo secolo prima, ma senza pubblicare.
Ufficialmente, il primo ad esporre una trattazione sistematica
dei sistemi di numerazione posizionali fu il matematico tedesco
G. W. Leibniz; anche se l’inglese T. Harriot ne aveva discusso
e scritto oltre mezzo secolo prima, ma senza pubblicare.
Leibniz, filosofo e teologo oltre che matematico, era affascinato
dal sistema binario; il fatto che nel sistema binaro tutti i numeri
possono essere rappresentati mediante due soli simboli
gli richiamava la creazione dell’universo, tratto dal nulla (0)
per opera di Dio (1).
[BJB, 265-267]
Ufficialmente, il primo ad esporre una trattazione sistematica
dei sistemi di numerazione posizionali fu il matematico tedesco
G. W. Leibniz; anche se l’inglese T. Harriot ne aveva discusso
e scritto oltre mezzo secolo prima, ma senza pubblicare.
Leibniz, filosofo e teologo oltre che matematico, era affascinato
dal sistema binario; il fatto che nel sistema binaro tutti i numeri
possono essere rappresentati mediante due soli simboli
gli richiamava la creazione dell’universo, tratto dal nulla (0)
per opera di Dio (1).
[BJB, 265-267]
La possibilità di rapppresentare ogni numero con soli due
simboli ha però un costo: la lunghezza della rappresentazione.
Infatti una cifra binaria (bit) ha capacità di esprimere
solo la minima quantità possibile di informazione.
Sistema babilonese sessagesimale posizionale (incompleto)
Sistema Maya ventesimale posizionale (incompleto)
Frazioni
Aritmetica bizzarra
“No Giacomo, non puoi fare cosı̀” disse il maestro indicando
il quaderno di Giacomo, su cui lo scolaro aveva scritto
1 8
18
× =
4 5
45
“Scusi, sgnor maestro” disse Giacomo. “Che c’è di sbagliato?
L’ho controllato con la calcolatrice e sembra che vada bene”.
“Be’, Giacomo, il risultato è giusto, direi” ammise il maestro.
“Anche se probabilmente dovresti semplificare in modo
da ottenere 2/5, che è ridotto ai minimi termini. Quello
che è sbagliato è...”.
[St, 173]
Sappiamo bene che
a
c
a·c
per la frazione è la frazione
;
b
d
b·d
ma perché è questa la definizione di moltiplicazione tra frazioni
e non magari la ricetta proposta da Giacomo?
il prodotto della frazione
Sappiamo bene che
a
c
a·c
per la frazione è la frazione
;
b
d
b·d
ma perché è questa la definizione di moltiplicazione tra frazioni
e non magari la ricetta proposta da Giacomo?
il prodotto della frazione
Un’occhiata ai due disegni che seguono dovrebbe persuaderci
che la definizione usuale corrisponde ai fatti.
4 3
12
4·3
× =
=
7 5
35
7·5
Il quadrato è l’unità e ogni rettangolino è 1/35 dell’unità. [Va, 15]
20 17
340
20 · 17
×
=
=
7
5
35
7·5
20 17 6 2 ×
= 2+ · 3+
7
5
7
5
=6+
4 18 12
+
+
5
7
35
68
340
5
=
=9
35
7
7
Per addizionare (spesso) occorre (almeno) moltiplicare:
a
c
a·d +b·c
+ :=
b d
b·d
Esempio:
4·5+7·3
20 + 21
41
6
4 3
+ =
=
=
=1
7 5
7·5
35
35
35
Altro esempio:
3
8
3 · 15 + 10 · 8
45 + 80
125
+
=
=
=
,
10 15
10 · 15
150
150
oppure
8
3 · 15 + 10 · 8
3·3·5+2·5·8
25
3
9 + 16
+
=
=
=
=
;
10 15
10 · 15
2·5·3·5
30
30
in ogni caso
125
25
5
=
= .
150
30
6
In fondo all’aula si sentı̀ la voce sommessa di Giacomo:
“Maestro, la sua formula per sommare è troppo complicata,
non potrebbe bastare
c
a
a+c
+ =
?
b d
b+d
Cosı̀ sarebbe simile a quella del prodotto
(che finalmente ho capito).”
[Bo] Bottazzini U. - Numeri - Raccontare la matematica Intersezioni - il Mulino - Bologna - 2015
[BJB] Bunt L.N.H., Jones P.S., Bedient J.D. - Le radici storiche
delle matematiche elementari - Zanichelli - Bologna - 1987
[St] Stewart I. - La piccola bottega delle curiosità matematiche
del professor Stewart - Codice edizioni - Torino - 2010
[Va] Valenti D. - Frazioni e numeri razionali - Treccani Scuola www.treccani.it/portale/opencms/Portale/resources/multimedia/
lezioni matematica/frazioni/Frazioni Presenta1.pdf