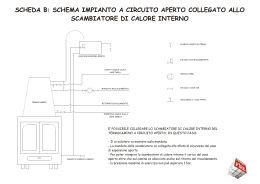
Università di Roma – Tor Vergata
Facoltà di Ingegneria – Dipartimento di Ingegneria Industriale
Corso di:
“TERMOTECNICA 1”
DIMENSIONAMENTO DEGLI SCAMBIATORI
DI CALORE
Ing. G. Bovesecchi
[email protected]
06-7259-7127 (7249)
Anno Accademico 2012-2013
Metodo ∆Tml
Dimensionamento degli scambiatori con il metodo ΔTml
Consideriamo uno scambiatore del tipo più semplice, a tubi
coassiali, equicorrente o controcorrente. Gli andamenti di
temperatura sono riportati nei grafici. Si vede come nello
scambiatore in equicorrente il fluido caldo rimane sempre a
temperatura superiore a quello freddo, mentre nel controcorrente
il fluido freddo in uscita può trovarsi a temperatura superiore al
fluido caldo in uscita. Per entrambe le configurazioni di moto
l’analisi può essere fatta mediante calcolo analitico.
Dobbiamo trovare un’espressione analitica che permetta di
calcolare l’andamento della differenza di temperatura tra fluido
caldo e freddo ΔT = (Tc-Tf) in funzione della distanza
dall’ingresso.
Metodo ∆Tml
Dalle:
dQ1 = − m c c cpdT c
dQ 2 = ± m f c pf dT f
Possiamo scrivere:
dQ1
dT = −
m c c cp
dQ 2
f
dT =
± m f c pf
c
Effettuando la differenza tra queste due equazioni si ottiene:
(
d T −T
c
f
)
⎛ 1
1 ⎞
1 ⎞
⎛ 1


= −dQ ⎜ c ± f ⎟
= −dQ ⎜
±
c
f ⎟
⎝ C
C ⎠
⎝ m c c p m f c p ⎠
Metodo ∆Tml
Indicando con C c e C f le capacità termiche di massa del fluido
caldo e di quello freddo. Uguagliando questa equazione con la
(
dQ 3 = UdA T c − T f
si ottiene:
(
d Tc −T f
Tc −T f
)
) = −UdA ⎛
1
1 ⎞
⎜⎝  c ±  f ⎟⎠
C
C
assumento che il flusso termico ceduto dal fluido caldo sia pari a
quello assorbito dal fluido freddo.
Integrando si ottiene:
2
2
d Tc −T f
1 ⎞
⎛ 1
=
−U
dA
±
∫1 T c − T f
∫1 ⎜⎝ C c C f ⎟⎠
(
)
dove 1 e 2 sono la prima sezione dello scambiatore e l’ultima.
Metodo ∆Tml
Non si tratta della sezione di ingresso e di quella di uscita dei
fluidi, ma di quella iniziale e quella finale dello scambiatore;
esse coincidono con quella di ingresso e quella di uscita dei
fluidi solo per la configurazione in equicorrente.
Se l’integrazione viene fatta sino alla generica lunghezza x dello
scambiatore porta a:
ln
ΔT (x)
1 ⎞
⎛ 1
= − ⎜ c ± f ⎟ UA(x)
⎝ C
ΔT (x)1
C ⎠
cioè
ΔT (x) = ΔT1e
1
⎛ 1
−⎜ c ± f
⎝ C C
⎞
⎟⎠ UA( x )
Metodo ∆Tml
Integrando tra i due estremi 1 e 2, invece
ΔT2
1 ⎞
⎛ 1
ln
= − ⎜ c ± f ⎟ UA
⎝ C
ΔT1
C ⎠
1
1
la quantità ⎛⎜ c ± f ⎞⎟ si ottiene dalle relazioni
⎝ C
C ⎠
Q1 = m c c cp Ti c − Tuc = C c Ti c − Tuc
Cioè:
(
)
(
)
(
)
Q 2 = m f c pf Tuf − Ti f = C f Tuf − Ti f
(
)
1 ⎞
⎛ 1
Q ⎜ c ± f ⎟ = Ti c − Tuc ± Tuf − Ti f
⎝ C
C ⎠
)
(
Metodo ∆Tml
Sostituendo nella relazione appena trovata la
ΔT2
1 ⎞
⎛ 1
ln
= − ⎜ c ± f ⎟ UA
⎝ C
ΔT1
C ⎠
si ottiene l’espressione del flusso termico scambiato dallo
scambiatore, cioè
(
)
Ti c − Tuc ± Tuf − Ti f
ΔT2 − ΔT1

Q = UA
= UA
ΔT2
ΔT2
ln
ln
ΔT1
ΔT1
Dal confronto tra questa relazione e la
(
Q 3 = UA T c − T f
)
Metodo ∆Tml
si nota come la differenza di temperatura media cercata è proprio
la frazione a secondo membro della
(
)
Ti c − Tuc ± Tuf − Ti f
ΔT2 − ΔT1

Q = UA
= UA
ΔT2
ΔT2
ln
ln
ΔT1
ΔT1
che assume la denominazione di differenza di temperatura media
logaritmica, da cui prende nome il metodo.
ΔT2 − ΔT1
ΔTml =
ΔT2
ln
ΔT1
Metodo ∆Tml
Si noti come l’espressione è la stessa sia per gli scambiatori in
equicorrente, che in controcorrente, a patto che per sezioni 1 e 2
si intendano, come detto sopra, le sezioni iniziale e finale dello
scambiatore, e non quelle di ingresso e uscita dei fluidi.
Le espressioni di ΔT1 e ΔT2 risultano chiaramente differenti in
termini di temperature di ingresso e uscita dei due fluidi.
Tra gli scambiatori elencati a inizio paragrafo, alcuni di quelli a
fascio tubiero e quelli a piastre realizzano la configurazione a
controcorrente quasi perfetta.
Si noti inoltre che nella configurazione in controcorrente le
differenze di temperatura tra fluido caldo e freddo sono in media
inferiori: pertanto si ha minore irreversibilità (che nella
trasmissione del calore è legata alla differenza di temperatura), e
conseguentemente minore generazione di entropia; cioè detto in
altri termini è necessaria una temperatura inferiore del fluido
caldo per ottenere lo stesso risultato.
Metodo ∆Tml
Nel caso che lo scambiatore non sia del tipo a tubi coassiali
(controcorrente o equicorrente perfetta), la relazione :
ΔT − ΔT
Q = UA
ΔT
ln
ΔT
2
1
2
1
viene scritta nel modo seguente:
Q = UAΔT
dove
ΔT = Ft ( ΔTml )cc
Con ( ΔT ) la differenza di temperatura media logaritmica per la
configurazione in controcorrente perfetta.
ml
cc
Metodo ∆Tml
Il fattore correttivo Ft è dato in opportuni grafici come funzione
dei due numeri adimensionali:
T −T
Ti c − Tuc
R= f
P=
f
Tu − Ti
T −T
f
u
f
i
c
i
f
i
!
Metodo ∆Tml
!
Grafico per uno scambiatore a fascio tubiero tipo 1-2 (il grafico
per lo scambiatore 1-2 vale anche per quello 1-4, 1-6 etc.). Si noti
che il numero adimensionale R può anche essere definito come
R = C C
f
c
Tale relazione si verifica facilmente dalle relazioni:
Q1 = C c Ti c − Tuc
Q 2 = C f Tuf − Ti f
(
)
(
)
Metodo ∆Tml
In alcuni grafici talvolta compare una curva che indica il valor
minimo di Ft , cioè quello al di sotto del quale generalmente non
si progetta uno scambiatore per evitare di utilizzare in modo non
efficiente l’area di scambio.
!
Metodo ∆Tml
In alcuni grafici talvolta compare una curva che indica il valor
minimo di Ft , cioè quello al di sotto del quale generalmente non
si progetta uno scambiatore per evitare di utilizzare in modo non
efficiente l’area di scambio.
!
Metodo ε-NTU
Per tale verifica non si conoscono le temperature di uscita dei due
fluidi, mentre lo scambiatore è conosciuto (dato), cioè si
conoscono C , C e UA.
Si individuano innanzi tutto tra le due capacità termiche di massa
C ,C quella di valor maggiore e quella di valore minore, cioè
C , C . Si definisce ora l’efficienza ε dello scambiatore il
rapporto tra il flusso termico effettivamente scambiato e quello
che verrebbe scambiato da uno scambiatore ideale, intendendo
con questa espressione uno scambiatore in controcorrente
perfetta di area infinita.
Consideriamo uno scambiatore in controcorrente, sono possibili
due casi, illustrati nel grafico seguente.
f
f
max
c
min
c
Metodo ε-NTU
c
T
T i
Tuf
c
T
T i
Tuc
Ti f
A
Tuf
Tuc
Ti f
A
!
Metodo ε-NTU
Sono possibili due casi:
  il primo se il fluido a capacità termica di
flusso maggiore è quello caldo (è quindi il
ΔTc = Tic - Tuc è minore del ΔTf = Tuf – Tif),
  il secondo al contrario.
Si noti anche come gli andamenti della
temperatura sono differenti nei due casi, perché
presentano nel primo caso concavità rivolta
verso il basso, nel secondo verso l’alto. Se ora si
immagina di estendere la superficie di scambio
termico dello scambiatore sino all’infinito, gli
andamenti di temperatura che si ottengono sono:
c
T Ti
Tuf
Tuc
Ti f
A
c
T Ti
Tuf
Tuc
Ti f
A
!
Metodo ε-NTU
c
T
i
T
Tuf
c
T
T i
Tuc
Ti f
A
Tuf
Tuc
Ti f
A
Da questi andamenti risulta chiaro come nel primo caso, per lo
scambiatore di area infinita, la temperatura di ingresso del fluido
caldo Tic coincide con la temperatura di uscita del fluido freddo Tuf ,
nel secondo caso invece è Tuc che coincide con Tif .
!
Metodo ε-NTU
In entrambi i casi succede che il flusso termico si può scrivere
Q = C ΔT = C (T − T )
c
ideale
min
max
min
f
i
i
essendo nel primo caso Tuf = Tic , e nel secondo caso Tuc = Tif
In definitiva l’efficienza dello scambiatore si può scrivere:
Q
Q
ε=
=

Q
C (T − T )
c
ideale
min
i
f
i
Questa espressione non contiene le temperature di uscita dei due
fluidi, per cui può essere utilizzata nel rate problem.
Si definisce inoltre il numero delle unità di trasporto NTU
(number of transport units), il rapporto tra il flusso termico
trasmesso per unità di differenza di temperatura media (ΔTm) tra i
due fluidi e
Metodo ε-NTU
il flusso termico corrispondente alla variazione di temperatura
unitaria per il fluido a capacità termica di flusso minore:
UA
NTU =
C
min
In generale risulta che l’efficienza ε è funzione di NTU e del
rapporto tra C e C , rapporto a volte indicato con il simbolo R,
anche se la sua definizione non coincide necessariamente con
quella dell’R del metodo ΔTml , dove è definito come rapporto tra
C e C . Gli andamenti di ε in funzione dell’NTU, parametrizzati
per diversi valori del rapporto R sono riportati in opportuni
grafici, relativi ciascuno ad un tipo diverso di scambiatori.
max
f
c
min
Metodo ε-NTU
!
Metodo ε-NTU
La procedura da seguire per effettuare la verifica di funzionamento
di uno scambiatore con il metodo ε-NTU è la seguente:
C il valore massimo e a
  si valutano i C e C , e si attribuisce a C
C il minimo;
C
  si calcola NTU dalla :
UA
NTU =
C
  dal diagramma ε = f ( NTU , R ) si ricava ε
  Dalla:
Q
Q
ε=
=

Q
C (T − T )
si ricava il flusso termico effettivamente scambiato
  dalle
f
c
max
min
min
c
ideale
Q = m c (T − T
c
1
c
p
c
i
u
c
)
min
f
i
i
Q = m c (T − T
f
2
si ricavano le temperature di uscita.
f
p
f
u
i
f
)
Metodo ψ-P
Sia il metodo ΔTml sia quello ε-NTU presentano degli
inconvenienti quando non sono utilizzati per le applicazioni per
cui sono stati ideati, cioè quando il metodo ΔTml viene usato nel
rate problem, e il metodo ε-NTU per il size problem. In tali caso il
calcolo è possibile, ma richiede soluzioni iterative, cioè si devono
ipotizzare dei valori delle variabili incognite (le dimensioni nel
metodo ΔTml utilizzato per il rate problem, e le temperature di
uscita dei fluidi , quando è usato il metodo ε-NTU nel size
problem), effettuare il calcolo e verificare se i risultati coincidono
con quelli conosciuti.
Per evitare tale problema si è introdotto il metodo ψ-P. Il numero
adimensionale P è lo stesso utilizzato per calcolare il fattore
correttivo Ft nel metodo ΔTml.
Metodo ψ-P
La quantità adimensionale ψ è definita come :
ψ=
ΔT
T −T
c
i
f
i
che rappresenta il rapporto tra la temperatura media effettiva dello
scambiatore e la differenza delle temperature in ingresso e uscita
dei due fluidi. Chiaramente :
ΔT = F ΔT
ml ,cc
t
e il flusso termico diventa :
Q = UAψ (T − T
c
i
i
f
)
il numero adimensionale ψ viene dato come funzione dei numeri
P e R, in opportuni diagrammi, in cui vengono anche riportati Ft ,
NTU.
Metodo ψ-P
Risulta per tanto il metodo di dimensionamento più generale, che
può essere utilizzato in ogni caso. In figura è riportato il
diagramma ψ-P per lo stesso scambiatore a fascio tubiero 1-2.
Metodo ψ-P
In pratica tutti i tre metodi di dimensionamento utilizzano tre
numeri adimensionali, di cui uno (dipendente) si ricava in
funzione di altri due. Nella tabella seguente sono riportati tali
numeri. Si noti infine che nel metodo ψ-P a seconda
dell’applicazione in cui viene utilizzato (size problem o rate
problem), alcune quantità riportate nel grafico possono essere
utilizzate come variabili dipendenti, per esempio NTU (da cui si
ricava l’area A nel size problem), o Ft .
Perdite di carico nei fasci tubieri
Negli scambiatori a fascio tubiero, dal lato tubi lo scambio
termico e le perdite di carico si calcolano nel solito modo
(correlazioni empiriche, equazione di Darcy Weissbach) tenendo
conto che oltre alle perdite di carico distribuite esistono come
minimo quelle concentrate dell’imbocco dalla prima camera di
distribuzione nei tubi e quelle dello sbocco nella camera di
raccolta (o di inversione).
Dal lato mantello il calcolo è più complesso: bisogna tenere
conto che il fluido passa attraverso un condotto di sezione
all’incirca rettangolare, definito dal mantello stesso e dai
diaframmi, in cui la sezione risulta variabile continuamente;
complessivamente il percorso del fluido deve anche passare da
un segmento (sempre delimitato dal mantello e da due diaframmi
consecutivi) e un altro.
Fascio tubiero
Vi è poi la superficie esterna dei tubi che contribuisce all’attrito.
Pertanto il deflusso è tortuoso e passa da parallelo a normale
all’asse dei tubi. Si utilizzano delle formule empiriche differenti
a seconda della disposizione dei tubi, che nella maggior parte dei
casi può assumere due configurazioni: a quadrato o triangolare.
s
s
d
disposizione a quadrato
d
disposizione triangolare
!
Perdite di carico nel fascio tubiero
Ad esempio per 2000 ≤ Re ≤ 106 si può utilizza la relazione:
⎛ µ⎞
Nu = 0, 36 Re Pr ⎜ ⎟
⎝µ ⎠
0 ,55
0 ,14
1/3
p
dove µ è la viscosità dinamica alla temperatura media del fluido,
mentre µp è alla temperatura della parete esterna dei tubi. La
velocità da utilizzare nel numero di Re va calcolata al centro del
mantello. La sezione di passaggio vale:
s − d )l d
(
A=
s
dove:
  s è la spaziatura dei tubi
  d è il diametro esterno dei tubi
  l è la distanza tra i diaframmi
  dm è il diametro del mantello
m
Perdite di carico nel fascio tubiero
La lunghezza caratteristica da utilizzare in Re e in Nu è il
diametro equivalente, che risulta:
4(s − π d / 4)
d =
πd
2
2
eq
per la configurazione a quadrato;
⎛ 3
πd ⎞ 1
d = 4⎜
s −
4 ⎟⎠ π d
⎝ 2
2
2
eq
per la configurazione a triangolo equilatero.
Le stesse quantità si utilizzano anche per le perdite di carico
distribuite.
Perdite di carico nel fascio tubiero
Nella progettazione effettiva di un impianto che richieda
scambiatori di calore, si utilizza una procedura, in genere
iterativa, che tenga conto sia dei dati di progetto che del costo.
Questo in entrambi i tipi di calcolo (size problem e rate
problem).
Nel seguito riportiamo un esempio di tale procedura valida per
gli scambiatori a fascio tubiero, anche se fondamentalmente la
sequenza di operazioni è simile per tutti i tipi di scambiatore.
1. Calcolare il carico termico;
2. Scegliere le temperature incognite e i flussi, quando non già
specificati;
3. Individuare una prima scelta del coefficiente di scambio totale;
4. Calcolare la superficie di scambio;
5. Sui dati già individuati (2-3) scegliere il tipo più appropriato di
scambiatore;
Perdite di carico nel fascio tubiero
6.  Per gli scambiatori a fascio tubiero determinare se è
necessario inserirne più di uno in cascata;
7.  Scegliere le dimensioni dei tubi, passo e disposizione;
8.  Scegliere il fluido dal lato tubi, numero di passaggi,
dimensioni del mantello e caduta di pressione;
9.  Calcolare lo scambio termico e la caduta di pressione;
10.  Controllare se le specifiche sono state rispettate, se no si
riinizia dal punto 8 con un’altra scelta di progetto;
11.  Stima dei costi;
12.  Sulla base dei costi totali e dimensioni, verificare la miglior
scelta dello scambiatore per l’impianto;
13.  Sottomettere il progetto ad un fabbricante per il progetto
meccanico e termico finale e per la costruzione.
Perdite di carico nel fascio tubiero
Per quanto riguarda il punto 3, si consideri che è normale
un’incertezza nella valutazione di h del 20% o anche maggiore.
Inoltre è opportuno che il fattore Ft del metodo ΔTml valga
almeno 0,75.
Per il punto 8, si noti che all’interno dei tubi viene in genere
posto il fluido meno viscoso (così si minimizzano le perdite di
carico e il costo del pompaggio), a maggiore pressione (perché la
tenuta è più facile nei tubi), che sporca o corrode di più (nei tubi
la velocità è maggiore, e tali inconvenienti a maggiore velocità
sono meno rilevanti).
Si noti infine che la caduta di pressione non dovrebbe superare
0,6 ÷ 0,7 bar, a meno che si abbiano liquidi molto densi o viscosi
(oli minerali, alimenti, etc.) per cui può arrivare a 1,4÷2 bar. Per
i gas a bassa pressione e i vapori in condensazione la perdita non
dovrebbe superrare il 5% della pressione assoluta.