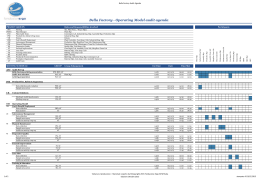
DINAMICA DI SISTEMI AEROSPAZIALI
Tema d’esame 08 - 09 - 2014
m, r, J
O
Cm
B
Ω
h
l1
F
l2
P
R
A
C
x
Esercizio 1. Il sistema in figura, posto nel piano
orizzontale, è composto da un disco di massa m,
raggio r e momento d’inerzia baricentrico J, collegato a terra tramite due aste incernierate alle estremità, di lunghezza rispettivamente pari a l1 e l2 e
di massa trascurabile rispetto ad m. Il disco stesso si trova in contatto con una guida circolare di
raggio R e centro in C. Applicata al suo centro
agisce inoltre una forza F , costante in modulo e direzione.
1.a: Scrivere le espressioni di posizione, velocità e accelerazione del punto B, centro del disco, in funzione
della rotazione dell’asta OA, nella condizione in cui a quest’ultima sia imposta una velocità di rotazione
costante Ω;
1.b: la coppia motrice Cm necessaria a mantenere le condizioni di moto definite al punto precedente;
1.c: le reazioni scambiate fra disco e guida circolare nel punto di contatto P, nella condizione di moto
definita ai punti precedenti.
Jm
Jd , R
Esercizio 2. Un motore elettrico in corrente continua
ωu τ, ηd , ηr ωm Cm
M caratterizzato da coppia motrice Cm = Ke ia , resistenM
T
za Ra , tensione di alimentazione ea ed induttanza trascurabile muove, attraverso una trasmissione T i cui rendimenti,
rispettivamente di moto diretto e retrogrado, sono ηd e ηr ,
un disco di raggio R e momento d’inerzia baricentrico Jd .
g
Sul disco si avvolge una fune inestensibile alla cui estremità
è collegata una massa m. Il sistema è posto nel piano vertim
cale.
Si determinino:
2.a: il momento d’inerzia baricentrico del volano Jm che garantisce all’avviamento in discesa che l’accelerazione di m sia a ≪ g;
2.b: l’intervallo di valori di coppia motrice Cm per cui sussistono condizioni di equilibrio statico;
2.c: le reazioni scaricate al telaio dalla trasmissione nelle condizioni del punto 2.a.
Esercizio 3. Il sistema in figura è posto nel piano orizzontale
ed è costituito da un pistone di massa mp , mosso da un manovellismo ordinario centrato la cui manovella ha lunghezza r e la
biella lunghezza l, con r ≪ l. Entrambe hanno massa trascurabile
rispetto alla massa del basamento M . La manovella ruota a velocità costante Ω. Il basamento, è vincolato a traslare in direzione
y ed è sospeso da due elementi elastici di pari rigidezza k.
mp
l
k
y
x
r
M
Ω
A
k
3.a: Scrivere l’equazione di moto del sistema, semplificando
il contributo del sottosistema biella-manovella con una
approssimazione del primo ordine;
3.b: determinare l’espressione della forza totale trasmessa dal
basamento al telaio;
3.c: disegnare il grafico qualitativo dell’andamento dell’ampiezza di vibrazione della massa M in funzione della velocità
angolare Ω della manovella.
N.B.: si definisca e si commenti opportunamente qualsivoglia dato ritenuto mancante.
Traccia di soluzione.
Esercizio 1
Siano AO = ℓ1 eiα (α̇ = Ω, costante), BA = ℓ2 eiβ , BC = (r+R)eiγ , CO = x−ih, con
√
x2 + h2 < ℓ1 +ℓ2 +r+R.
1.a) Cinematica del punto B
La posizione, velocità e accelerazione del punto B sono date da
OB = ℓ1 eiα + ℓ2 eiβ
(1)
~vB = iα̇ℓ1 eiα + iβ̇ℓ2 eiβ
~aB = i✓
α̈ℓ1 e
iα
2
− α̇ ℓ1 e
iα
= iΩℓ1 eiα + iβ̇ℓ2 eiβ
+ iβ̈ℓ2 e
iβ
2
− β̇ ℓ2 e
iβ
2
= −Ω ℓ1 e
iα
+ iβ̈ℓ2 e
(2)
iβ
2
− β̇ ℓ2 e
iβ
(3)
Occorre determinare gli angoli α e β e le loro derivate.
La chiusura del poligono OABC dà
AO + BA = CO + BC
(4)
ovvero
ℓ1 eiα + ℓ2 eiβ = (r + R)eiγ + x − ih
(5)
in cui le variabili sono α, β e γ. È quindi possibile determinare β e γ in funzione di α.
Dalla derivata dell’equazione di chiusura si ricava
iΩℓ1 eiα + iβ̇ℓ2 eiβ = iγ̇(r + R)eiγ
ovvero
ℓ2 sin β −(r + R) sin γ
−ℓ2 cos β (r + R) cos γ
da cui
β̇
γ̇
1
=
ℓ2 (r + R) sin(β − γ)
(6)
β̇
γ̇
=
−ℓ1 sin α
ℓ1 cos α
Ω
(7)
(r + R) cos γ (r + R) sin γ
ℓ2 cos β
ℓ2 sin β
−ℓ1 sin α
ℓ1 cos α
Ω
(8)
e quindi
ℓ1 sin(β − α)
γ̇
=
Ω
r + R sin(β − γ)
(9)
Analogamente, dalla derivata seconda dell’equazione di chiusura si ricava
−Ω2 ℓ1 eiα + iβ̈ℓ2 eiβ − β̇ 2 ℓ2 eiβ = iγ̈(r + R)eiγ − γ̇ 2 (r + R)eiγ
ovvero
ℓ2 sin β −(r + R) sin γ
−ℓ2 cos β (r + R) cos γ
β̈
γ̈
=−
ℓ1 cos α
ℓ1 sin α
2
Ω −
(10)
ℓ2 cos β
ℓ2 sin β
2
β̇ +
(r + R) cos γ
(r + R) sin γ
γ̇ 2
(11)
1.b) Coppia motrice
Si consideri il teorema dell’energia cinetica. La velocità del punto B, espressa in funzione del movimento
associato al segmento BC, è (r + R)γ̇, diretta tangenzialmente in modo tale che, per γ̇ > 0, il punto B orbita
attorno al punto C in senso antiorario. Siccome al contatto in P tra disco e guida la velocità è nulla, per
l’ipotesi di puro rotolamento, la velocità angolare del disco φ̇, oraria, è tale per cui rφ̇ = −(r + R)γ̇, ovvero
φ̇ = −(1 + R/r)γ̇.
L’energia cinetica del sistema è
!
1
1 2 1
R 2
2 2
2
Ec = m(r + R) γ̇ + J φ̇ =
γ̇ 2
(12)
m(r + R) + J 1 +
2
2
2
r
La potenza delle forze attive è
Π = Cm Ω − F (r + R) cos γ γ̇
Dal teorema dell’energia cinetica si ricava quindi
2 !
R
m(r + R)2 + J 1 +
γ̈ γ̇ = Cm Ω − F (r + R) cos γ γ̇
r
(13)
(14)
ovvero
!
R 2
∂γ
∂γ
m(r + R) + J 1 +
γ̈
= Cm − F (r + R) cos γ
,
r
∂α
∂α
2
(15)
ove ∂γ/∂α = γ̇/Ω.
1.c) Reazioni in P
Al contatto in P il disco e la guida si scambiano una reazione che può essere scomposta in componente
radiale, N , diretta come ~n (o eiγ ), e tangenziale, T , diretta come ~t = ~k × ~t (o ieiγ ). Si consideri l’equilibrio
alla rotazione del solo disco rispetto al proprio centro:
J φ̈ − T r = 0
(16)
con T in direzione sudovest nella configurazione del disegno. Si ottiene
T =
J
φ̈
r
(17)
Si consideri ora l’equilibrio alla rotazione dell’insieme disco e asta BA rispetto alla cerniera in A:
=0
J φ̈ + ~k · PA × ~nN + ~tT + BA × ~jF − m~aB
(18)
da cui, essendo T nota, si ricava N .
Esercizio 2
La potenza motrice è
Πm = (Cm − Jm ω̇m ) ωm
Ke
ea
−
ωm − Jm ω̇m ωm
= Ke
Ra
Ra
(19)
La potenza dell’utilizzatore è
Πu = (Cu − Ju ω̇u ) ωu = mgR − Jd + mR2 ω̇u ωu = τ mgR − τ 2 Jd + mR2 ω̇m ωm
(in quanto, stando al disegno, per ωu > 0 il peso scende).
(20)
2.a) Dimensionamento volano
All’avviamento in discesa il moto è retrogrado; ne consegue che la potenza fluisce dall’utilizzatore al motore,
quindi
Ke
ea
2
✟
Ke
−
ω
−
J
ω̇
Jd + mR2 ω̇m ✟
ω✟
ω✟
(21)
m
m m ✟
m + ηr τ mgR − τ
m =0
✟
Ra
Ra
da cui
Jm + ηr τ 2 Jd + mR2
ω̇m = Ke
ea
+ ηr τ mgR
Ra
(22)
Perché il moto sia effettivamente retrogrado, l’accelerazione deve essere positiva, in modo tale per cui la massa
inizia a scendere e quindi la potenza del peso della massa è positiva; questo accade se ea > −ηr τ mgRRa /Ke .
L’accelerazione allo spunto è
a = τ Rω̇m
Ke
ea + ηr τ mgR
Ra
= τR
Jm + ηr τ 2 (Jd + mR2 )
(23)
perché sia a ≪ g si deve avere
Ke
ea + ηr τ mgR
Ra
≪g
τR
Jm + ηr τ 2 (Jd + mR2 )
!
Ke
τR
ea + ηr τ mgR ≪ g Jm + ηr τ 2 Jd + mR2
Ra
!
1 Ke
τR
ea + ηr τ mR ≪ Jm + ηr τ 2 Jd + mR2
g Ra
!
1 Ke
Jm ≫ τ R
ea + ηr τ mR − ηr τ 2 Jd + mR2
g Ra
Jm ≫
τ R Ke
ea − η r τ 2 J d
g Ra
(24)
(25)
(26)
(27)
(28)
2.b) Equilibrio statico
Si ha equilibrio statico per moto incipiente verso il basso quando il sistema è in condizione di moto retrogrado
incipiente,
Cm✟
ω✟
ω✟
m + ηr τ mgR✟
m =0
(29)
ovvero
Cm = −ηr τ mgR
(30)
Si ha equilibrio statico per moto incipiente verso l’alto quando il sistema è in condizione di moto diretto
incipiente,
ω✟
ω✟
ηd Cm✟
m =0
m + τ mgR✟
(31)
ovvero
Cm = −
1
τ mgR
ηd
(32)
Quindi si ha equilibrio statico per
−
1
τ mgR < Cm < −ηr τ mgR
ηd
(1/ηd > ηr dato che 0 ≤ η ≤ 1).
(33)
2.c) Reazioni scaricate dalla trasmissione
La trasmissione riceve da un lato la coppia motrice Cm e dall’altro la coppia dell’utilizzatore, Cu . Quest’ultima in condizioni di avviamento vale Cu = mgR − (Jd + mR2 )ω̇u . La coppia motrice invece è Cm =
Ke ia − Jm ω̇m . La coppia complessiva Ct scaricata sui supporti dalla trasmissione è quindi
Ct = Cm + Cu
(34)
quindi vale
Ct = Ke ia − Jm ω̇m + mgR − (Jd + mR2 )ω̇u = Ke ia + mgR − (Jm + τ (Jd + mR2 ))ω̇m
(35)
Esercizio 3
La distanza tra il pistone e il punto A è u; detto α l’angolo di manovella, e β quello di biella, l’equazione di
chiusura dà
u = r cos α + ℓ cos β
r sin α = ℓ sin β
da cui è immediato ricavare sin β = (r/ℓ) sin α e quindi
r
r 2
u = r cos α + ℓ 1 +
sin2 α
ℓ
Considerando un’approssimazione del primo ordine si ottiene
p
u = r cos α + ℓ 1 + ε2 ∼
= r cos α + ℓ
(36)
(37)
(38)
(39)
3.a) Equazione di moto
Detto z lo spostamento del basamento, lo spostamento assoluto del pistone è zp = z + r cos α + ℓ. La sua
derivata è żp = ż − Ωr sin α. L’energia cinetica del sistema è
1
1
Ec = mp (ż − Ωr sin α)2 + M ż 2
2
2
(40)
L’energia potenziale è
1
Ep = 2 · kz 2
2
(41)
La corrispondente equazione di Lagrange di secondo tipo è
∂Ec
= mp (ż − Ωr sin α) + M ż
∂ ż
d ∂Ec
= (mp + M ) z̈ − mp Ω2 r cos α
dt ∂ ż
∂Ec
=0
∂z
∂Ep
= 2kz
∂z
Qz = 0
(42)
(43)
(44)
(45)
(46)
da cui
(mp + M ) z̈ + 2kz = mp Ω2 r cos α
(47)
3.b) Forza totale trasmessa a terra
La forza trasmessa a terra è f = 2kz; la si ricava determinando la soluzione a regime z = Z cos(Ωt), dato
che α = Ωt, quindi
−Ω2 (mp + M ) + 2k Z = mp Ω2 r
(48)
e
Z=
mp Ω2 r
2k − Ω2 (mp + M )
(49)
quindi la forza trasmessa è
f=
2kmp Ω2 r
cos(Ωt)
2k − Ω2 (mp + M )
(50)
e il suo massimo è
fmax =
2kmp Ω2 r
2k − Ω2 (mp + M )
(51)
3.c) Diagramma dello spostamento
Per Ω = p
0 lo spostamento è nullo; cresce inizialmente circa parabolicamente; tende ad un asintoto verticale
per Ω = 2k/(M + mp ); infine, per Ω → ∞ tende a −r/(1 + M/mp ).